Introduction
On the way towards a low-carbon future, electricity networks are considered as enablers and one of the critical areas to be studied under the Strategic Energy Technologies Plan. The first European Electricity Grid Initiative –EEGI– Roadmap 2010-2018 was approved by the European Commission and the Member States alongside the creation of EEGI in June 2010. The EEGI Roadmap defines the research, development and demonstration challenges that both European transmission and distribution system operators should address in the next years with the aim to face the requirements linked to the evolution of power systems and to respond to different external factors. For this reason, smart-grid projects are receiving a lot of attention (Hübner & Prüggler, 2011; Giordano et al., 2011; Losa, De Nigris & Van, 2013). New perspectives emerge for energy management. Many smart meters and sensors are being deployed and they result in a new data deluge we will have to face. With the rollout of smart metering infrastructure at scale, demand-response programs may now be tailored based on users’ consumption and production patterns as mined from sensed data.
Energy efficiency and sustainability are important factors to address in the context of smart cities. In this sense, a necessary functionality is to reveal various preferences, behaviors, and characteristics of individual consumers and prosumers, considering the fine-grained energy consumption and production information from smart meters, respectively. Smart metering and nonintrusive load monitoring play a crucial role in fighting energy thefts and for optimizing the energy consumption of the home, building, city, and so forth (Fenza, Gallo & Loia, 2019; Ahmad et al., 2018). Besides, it is very important to reduce the mismatch between the actual and expected energy demand, which is often due to an anomalous operation of the equipment and control systems. In this context, the characterization of energy consumption patterns over time is of fundamental importance (Capozzoli et al., 2018).
To the best of our knowledge, all approaches are still in a research phase, especially when it comes to clustering methods consumption and production data to provide clusters for each consumer and prosumer profile (Hossain et al., 2011; Binh et al., 2010; Figueiredo et al., 2005; Mutanen et al., 2011; Lee, Haben, & Grindrod, 2014; Ardakanian et al., 2014; Lavin & Klabjan, 2014).
While some authors have been working on grouping consumers considering the similarity among time series models, such as ARMA and ARIMA (Brockwell & Davis, 2002); others have been focusing on grouping consumers considering the time series as feature vectors (Flath et al., 2012; Cao, Beckel, & Staake, 2013). Most of the proposals model the data following only a local point of view, others only global, and others considering the original time series, which limits the analysis. The most successful approaches have been those that combine various clustering methods (Figueiredo et al., 2005; Albert & Rajagopal, 2013; Räsänen et al., 2010; Räsänen & Kolehmainen, 2009). It is even possible to find some proposals that combine clustering with other machine learning techniques, such as association rules (Funde et al., 2019). Nevertheless, those hybrid approaches only exploit the combination of clustering methods in order to mitigate the disadvantages of ones and enhance the benefits of others. However, they do not exploit other important reasons for developing hybrid time series clustering models.
Due to the limitations expressed above, in this paper, we introduce a general methodology that combines clustering methods in two stages and exploits in a hybrid way local and global patterns of the series under analysis. Our proposal can be used to group energy consumers and prosumers according to the similarity of their daily and yearly consumption and production, respectively. Thus, characteristic load and production profiles per time period can be determined, as we will explain later. The obtained results are generally applicable and will be useful in a general business analytics context.
Cluster analysis of smart meter data
Smart meter data are time series; which makes the analysis quite complex. For that reason, cluster analysis of consumption data has been explored in some papers (Hossain et al., 2011; Binh et al., 2010; Figueiredo et al., 2005; Mutanen et al., 2011; Lee et al., 2014; Ardakanian et al., 2014; Lavin & Klabjan, 2014), not so much the clustering of production data. From now on we will refer to consumption data clustering approaches; however, all proposals are applicable to production data clustering as well. Most authors have been focused on grouping consumers considering the time series as feature vectors. In literature four approaches are proposed to cope with the feature vector definition:
-
Consider features as interval consumption measurements (e.g., every 15 minutes) (Flath et al., 2012; Cao et al., 2013).
-
Only use global features (e.g., mean and standard deviation of an overall day) for characterizing each consumer (Lavin & Klabjan, 2014; Räsänen & Kolehmainen, 2009).
-
Extend the time series data by additional global features or other external measures (Ardakanian et al., 2014).
-
Create local patterns for characterizing the time series (Lee et al., 2014; Dent et al., 2011).
The first one follows a raw-data-based approach, the last two follow a feature-based approach and the third one considers an extension of the raw data including other features.
The definition of a distance measure between time series is necessary for the four approaches (Iglesias & Kastner, 2013), and it depends on the clustering objective, which can be similarity in time, similarity in shape or similarity in change (Zhang et al., 2011):
-
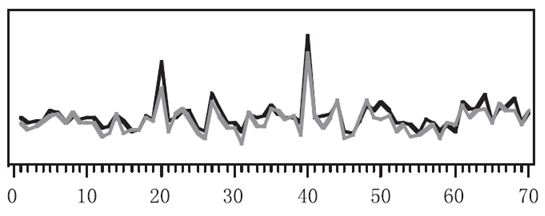
The similarity in time is to cluster together series that vary in a similar way on each time level, as shown in Figure 1 . Usually, the clustering of time series data based on similarity in time requires the calculation of the exact distances among all the time series data in a dataset.
-
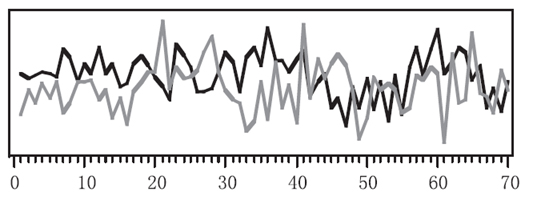
The similarity in shape is to cluster series with common shape features together, as shown in Figure 2 . This may constitute identifying common trends occurring at different times or similar sub-patterns in the data.
-
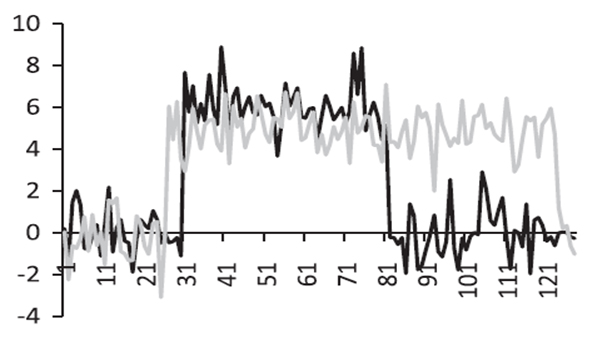
The similarity in change is to cluster series by the similarity in how they vary from time level to time level, as shown in Figure 3.
In this research, we are interested in time series clustering where the main clustering objective is the similarity in time because we need to cluster together series that vary in a similar way at each time interval. For this reason, in the first approach, it is necessary to define a distance measure based on the specific characteristics of time series data. Secondly, the arithmetic means of the single time segments are the starting point for the formation of global consumer behavior, but global features only do not properly represent the customers’ behavior. Thus, the second approach is not enough to segment the customers, and make groups of households with similar consumption patterns and determine on the fly the cluster membership of a given load curve. In the third approach, the dimensionality of the time series is increased and it could be difficult to manage different kinds of features, global and local in the same clustering process. Finally, the last approach could be useful for detecting clusters with similar load profiles, but it could be depending on the homogeneity of the data from the global feature point of view.
As we pointed out, the above approaches have some advantages and disadvantages. Thus, some authors prefer to develop hybrid approaches for time series clustering in other to solve the above disadvantages (Zhang et al., 2011; Lai et al., 2010; Aghabozorgi et al., 2014; Warren, 2007; Oates, Firoiu & Cohen, 1999; Aghabozorgi, Saybani & Wah, 2012). There are several reasons for developing hybrid time series clustering models (Lai et al., 2010). For instance, we might obtain very different clustering results for the same time series dataset when different time granules are considered. For time series clustering, dimensionality reduction methods are often applied to reduce the data dimension before clustering. Consequently, the information of subsequence may be overlooked. Therefore this might result in different clustering results after considering the subsequence information. Some conventional clustering methods require prior information and domain knowledge; others do not require prior information but are too computationally expensive to be applied on very large data sets. The combination of clustering methods can mitigate the disadvantages of some and enhance the benefits of others. For some applications, the clustering objective might not be that apparent. The selection of the time series representation and the similarity measure depends on the clustering objective. Thus, different clustering approaches are required.
Some hybrid clustering methods are proposed in the area of clustering analysis of smart metering data (Figueiredo et al., 2005; Albert & Rajagopal, 2013; Räsänen et al., 2010; Räsänen & Kolehmainen, 2009). Most of them apply Self-Organizing Maps –SOM– (Kohonen, 1982) in the first level and k-means (MacQueen, 1967) or hierarchical clustering algorithms (Räsänen et al., 2010) in the second level. SOM is used to obtain a reduction of the dimension of the initial dataset and k-means is used to group the weight vectors of the SOM’s units and the final clusters are obtained (Figueiredo et al., 2015; Räsänen et al., 2010; Räsänen & Kolehmainen, 2009). Another approach applies k-means first and uses spectral clustering to segment a collection into classes of similar statistical properties (Albert & Rajagopal, 2013). These hybrid approaches only exploit the combination of clustering methods in order to mitigate the disadvantages of ones and enhance the benefits of others. However, they do not exploit other important reasons for developing hybrid time series clustering models.
General ideas, stages, and schema of the proposed methodology
We introduce a general methodology that can be used to group time series considering different time granules. The proposed methodology consists of the following stages, as shown in Figure 4.
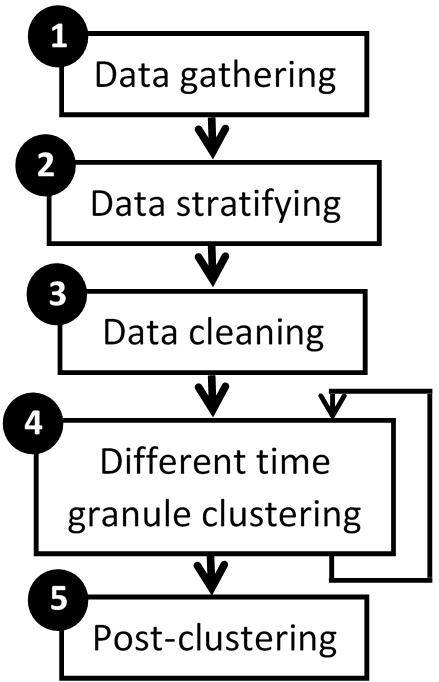 Figure 4
General schema of the proposed methodology
Figure 4
General schema of the proposed methodology
Source: Own elaboration.
Stage 1: Data gathering. Read time series; e.g., the time intervals of interest for data representation are typical 1 min, 15 min or 1h in the context of smart metering applications (Chicco, 2012).
Stage 2: Data stratifying. Segment the data, which separates the raw data sets into more homogeneous subsets, in order to sustain scalability; e.g., data can be stratified using a split between weekend and weekdays, or between summer and winter months when we are working with smart metering data (Flath et al., 2012; Cao et al., 2013).
Stage 3: Data cleaning. Detect and remove errors and inconsistencies from data in order to improve the data quality. In the smart metering domain some strategies can discard data sets showing more than one hour of recording gaps (Flath et al., 2012); check for inconsistencies in the data and remove outliers (Figueiredo et al., 2005); detect missing values and replace them using regression techniques (Figueiredo et al., 2005); remove special days (e.g., public holidays) (Cao et al., 2013); remove non-continuous data (McLoughlin, Duffy & Conlon, 2012).
Stage 4: Different time granule clustering. Select the time granule before clustering. Depending on the granularity level desired in the clustering, it is defined all the elements that contribute to the clustering. This stage can be repeated several times depending on how much you want to refine the level of granularity in the data analysis. This is the most important stage of our methodology. For that reason, we will explain in detail its main steps:
-
4.1 Time granule selection
-
4.2 Data representation
-
4.3 Data preprocessing
-
4.4 Distance/similarity selection
-
4.5 Clustering algorithm selection
Stage 5: Post-clustering. Apply clustering validation techniques, visualize the clustering results and obtain labels and prototypes for each cluster. For example, a useful post-clustering result in the smart metering applications can be the calculation of the global power and energy information for the customer classes for tariff setting purposes (Chicco, 2012).
The selection of the level of granularity is closely associated with the objective of the desired clustering, as shown in Figure 5. In this step, it is necessary to decide if the objective is the similarity in shape, in change or in time. The selection of the time series representation (raw-data-based, feature-based or model-based representation) also depends on the clustering objective. For example, if the objective is the similarity in time then we suggest using raw-data-based representation. On the other hand, if the objective is the similarity in change, we suggest using a model-based representation. We can change the representation in different clustering levels.
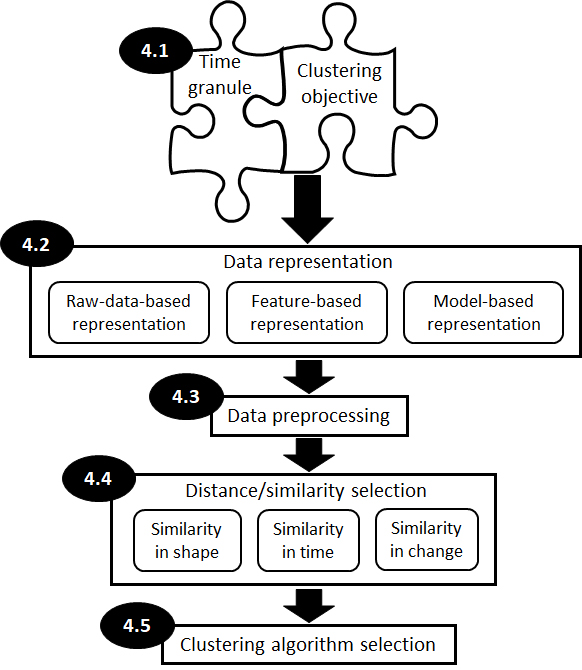 Figure 5
Stage 4 schema
Figure 5
Stage 4 schema
Source: Own elaboration.
Then, preprocessing is in charge of applying dimensionality reduction and normalization methods in correspondence with the clustering objective and the selected representation. Finally, it is necessary to define the appropriate distance measure and apply a clustering algorithm for obtaining clusters where all the series grouped in the same cluster should be coherent or homogeneous. It is important to take into account which is our clustering objective for deciding which distance measure we will apply. For example, if the clustering objective is the similarity in shape, then it will be useful to apply Dynamic Time Warping –DTW– distance. The most used algorithms are k-means (Lavin & Klabjan, 2014; Flath et al., 2012; Räsänen & Kolehmainen, 2009), Self-Organizing Maps –SOM– (Figueiredo et al., 2005; McLoughlin et al., 2012), hierarchical approaches (Cao et al., 2013) and Expectation Maximization (Albert & Rajagopal, 2013); as well as hybrid approaches (Figueiredo et al., 2005; Albert & Rajagopal, 2013; Räsänen et al., 2010; Räsänen & Kolehmainen, 2009).
Stage 4 offers the possibility to design procedures for different clustering objectives using diverse granules in the time series representation. Taking into account the smart metering domain, it could be useful in the first clustering level to group consumption or production data considering their voltage level combined with general global features; thus, a normalization process, in the second level, could be carried out inclusive a similarity in time objective clustering. In the case of high dimensional series, it could be useful to apply a feature-based representation in the first clustering level, and after that, refine the clustering results considering the raw-representation in the second level.
Two-level clustering approach based on local and global features
In this section, we apply the general architecture outlined in the previous section, to the smart grid data introduced earlier. More specifically, we apply a two-level clustering approach. The first level of clustering is based on features extracted from the time series. Regardless of the length of the time series and missing values, a finite set of statistical measures is used to capture the nature of the time series. The feature values are obtained from each individual series and can be fed into some specific clustering algorithm. In the first level, we propose to cluster data using only global features in order to divide consumers or prosumers considering their daily consumption or production data, respectively. In the second level, we split the obtained clusters in the first level, considering local features for discovering sub-clusters for each consumption or production profile. Features are obtained by applying statistical operations that best capture the underlying characteristics of the time series, depending on the clustering objective. Thus, a feature-based representation is used at both levels; nevertheless, the clustering objective is different in each level. The main objective is clustering considering the similarity in time.
Transforming the raw time-series data into the set of features has been used by several authors (Räsänen & Kolehmainen, 2009; Wang, Smith & Hyndman, 2006; Wang et al., 2004; Nanopoulos, Alcock, & Manolopoulos, 2001). Feature-based representation has several advantages; we will mention some of them. When the time series is very long (high dimensionality), some clustering algorithms become intractable; for instance, fail because the similarity is dubious in high dimension space. Applying dimensionality reduction via feature extraction, we are able to cluster long length time series very efficiently. Despite the length of the time series and missing values, a finite set of statistical measures can be used to capture the global and local nature of the time series. Furthermore, feature extraction is used to compress large data sets by means of dimensionality reduction. When the clustering algorithm is based on a distance metric (e.g., Euclidean distance), it cannot handle time series with missing data or of different lengths if actual points are used as inputs. However, by extracting a set of measures from the original time series we simply bypass this problem. Computational efficiency can be increased and the use of more sophisticated clustering algorithms is possible. When the clustering objective is the similarity in shape, it is possible to obtain good results using a feature-based representation.
Nevertheless, feature-based representation has some disadvantages; we will mention some of them. The majority of feature extraction methods are generic in nature, the extracted features are usually application dependent. Thus one set of features that work well on one application might not be relevant to another. When the clustering objective is the similarity in time, it is not possible to obtain good results using global features extracted from the time series.
Considering the above-mentioned advantages and disadvantages, and bearing in mind the objective of the clustering at each level, we propose to obtain two kinds of features at each level. Figure 6 shows the general schema of the proposed two-level clustering approach based on local and global features.
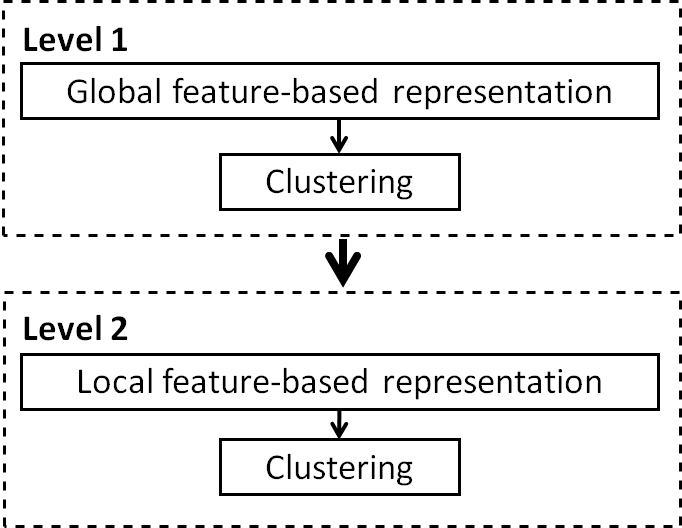 Figure 6
General schema of our two-level clustering approach based on local and global features
Figure 6
General schema of our two-level clustering approach based on local and global features
Source: Own elaboration.
In the first level, we propose to cluster data using only global features in order to divide consumptions or productions considering general behaviors. The principal global features to compute are mean, minimum, maximum and sum considering the total original features (e.g., 96 features if we consider 15 min interval consumption or production during a day). The clustering results can be improved if we include other features such as median, mode, standard deviation, variance, skewness, kurtosis, range, trend, seasonality, periodicity, serial correlation and chaos (Wang et al., 2006). Using a global feature-based representation, the dimensionality of the time series is significantly reduced and the clustering algorithm is much less sensitive to missing or noisy data. These features are enough to obtain clusters of consumers or prosumers with the same consumption or production levels and general characteristics, respectively; but they are not enough for generating clusters for each consumption or production profile per time period, because they cannot identify peaks at specific time periods.
In the second level, we split and refine the obtained clusters at the first level, considering local features for discovering sub-clusters. The local features express other information than the global features and emphasize the original time series characteristics. For characterizing the time series locally, it is possible to define a one hour, one week, or one day window, depending on the original time period. If we are processing daily profiles, a one hour window is used. A one day window is used for processing yearly profiles. We created four features for each window, computing mean, maximum, minimum and range, respectively. These local values allow expressing the time series behavior in each specified window. The clustering results can be improved if we include other features such as median, mode, standard deviation, variance, skewness, kurtosis, range, trend, seasonality, periodicity, serial correlation and chaos (Räsänen & Kolehmainen, 2009; Wang et al., 2006).
We currently explore suitable clustering methods and the choice of parameters that enable us to obtain general and specific clusters considering global and local features, respectively. The most used clustering methods are k-means (MacQueen, 1967), linkage (Defays, 1977), spectral clustering (Shi & Malik, 2000) and SOM (Kohonen, 1982). Useful similarity measures for these algorithms are Euclidean, cosine, correlation, and Manhattan (Iglesias & Kastner, 2013). We applied the k-means clustering algorithm (MacQueen, 1967) on global features in the first level for fixing a reasonable number of clusters to be obtained. The Complete Linkage clustering algorithm (Defays, 1977) was applied to the second level. The Euclidean distance was used for comparing the vectors in the cluster because it is a good distance when the clustering objective is the similarity in time.
A study case on belgian data
In Belgium, the authority on energy policy is shared between the federal and the regional administrations. The competent authority for the smart metering roll-out in Flanders is the regional energy regulator, VREG, while there are two Distribution System Operators –DSO–: Eandis and Infrax (European Commission, 2014; Renner & Heinemann, 2011).
There are few studies on profile identification and consumer segmentation in Belgium (Espinoza et al., 2005; Alzate et al., 2009). The least recent result starts from consumption data containing hourly consumption values from substations within the Belgian grid. The typical daily profile for each consumer is first identified, and, after that, the k-means algorithm is applied for capturing the different profiles. A large dataset of over 1300 load profiles of residential customers forms the basis for modeling in the most recent result. Each load profile is a sequence of measured data, with a resolution of 15 min, over the duration of one year. A multiway spectral clustering without the use of pre-modeling steps was used to detect consumer profiles.
In the research presented in this paper, we use real-life data, provided by Eandis. Houses in Belgium are connected to the electricity grid of the DSO and they are organized in neighborhoods of different sizes. All houses in a given neighborhood are connected via the low-voltage grid to one substation of the DSO. The dataset is comprised of aggregated 15 min intervals of electricity consumption and production of 2928 homes from 44 substations in Belgium.
Our objective is to apply the proposed methodology, specifically the two-level clustering algorithm, to detect the consumption and production profiles considering the customer behaviors in order to contribute to future decision-making problems in this field.
Consumer and prosumer data
The structure of a consumer or prosumer data is provided in a table, where each row represents a consumption or production day of one consumer or prosumer, respectively, and each numbered column represents a 15 min consumption or production interval, respectively.
The consumption behaviors change depending on weekends or weekdays. Figure 7 shows the daily consumption of a particular house for one week. Since there is a lot of variability over the different days it is not possible to identify an overall consumer profile. Figure 8 illustrates different behaviors in a specific weekend for one consumer. Notice that it is not possible to detect a weekend profile for this consumer. Figure 9 shows the daily consumption series from Monday to Friday for the same consumer. The profiles for weekdays are clearer than for the weekend considering this particular example. Thus, we are interested in the detection of consumption and production profiles, these profiles do not necessarily coincide with the consumers and prosumers profiles.
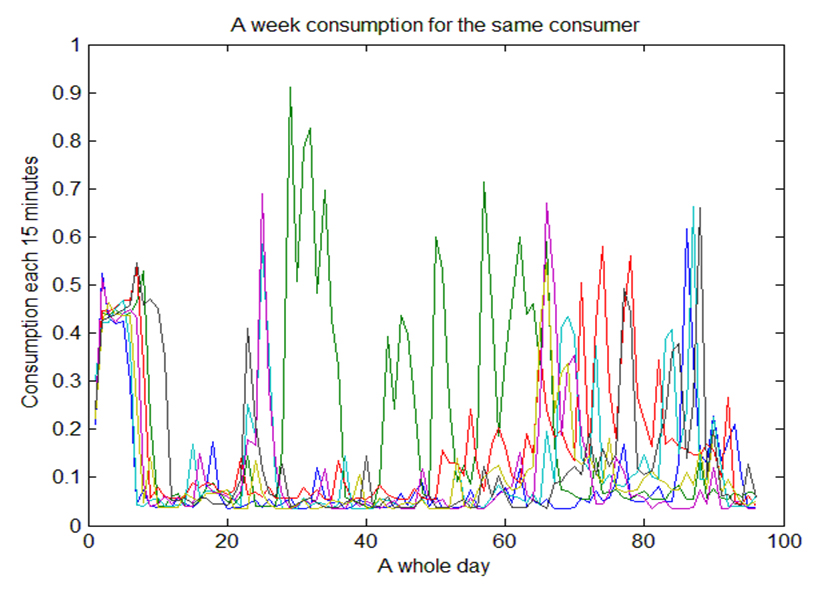 Figure 7
Daily consumption of a house in a whole week
Figure 7
Daily consumption of a house in a whole week
Source: Own elaboration.
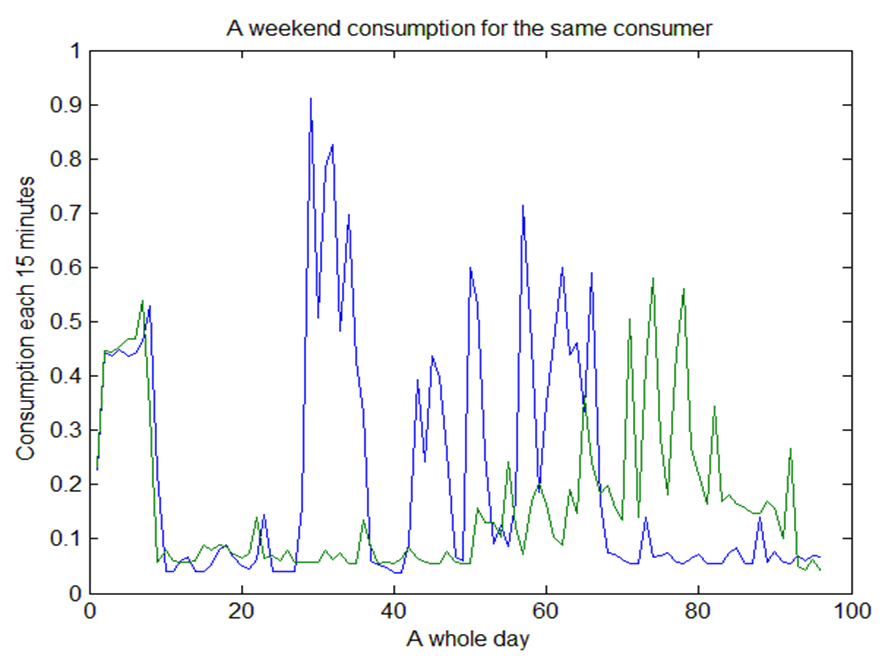 Figure 8
Daily consumption of a house in a weekend
Figure 8
Daily consumption of a house in a weekend
Source: Own elaboration.
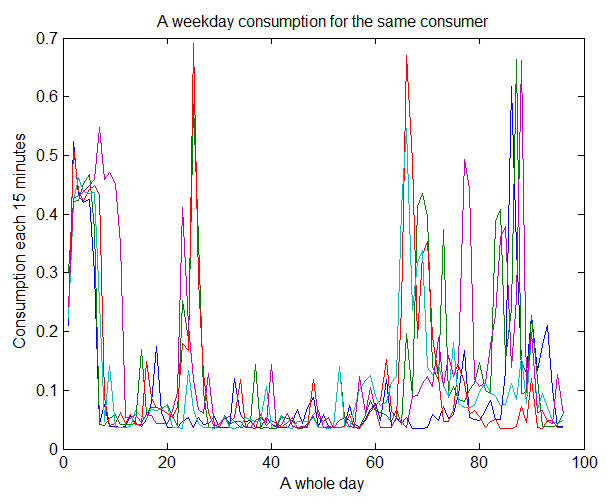 Figure 9
Daily consumption of a house for weekends
Figure 9
Daily consumption of a house for weekends
Source: Own elaboration.
Figure 7, Figure 8 and Figure 9 suggest the necessity of segmentation of the analysis considering weekends and weekdays separately. This is one criterion for splitting the raw data sets into more homogeneous subsets, besides it supports scalability. The seasonality effect also influences the shape of the profiles.
Experimental results
We applied the two-level clustering approach based on local and global features to the dataset with the electricity consumption and production of 2928 homes from 44 substations in Belgium, considering the period between 1st of November 2013 and 31st of October 2014.
Discovering typical daily consumption and production profiles is the main objective. Further, we want to discover the most typical consumers and prosumers considering their yearly consumption and production behavior, respectively. To this extent, four experiments were designed.
Daily consumption and production profiles
We prepared two datasets for discovering daily profiles. One with daily consumption and the other with the daily production values. Each time series consists of 96 energy consumption or production intervals. The global features were obtained by computing the mean, minimum, maximum, sum, median, standard deviation, variance and range considering the 96 original features for each daily consumption or production vector. For the second level, we created local features in order to refine the initial clustering results. The local features have to express more information than the original time series and global features. Thus, we created four features for each hour (i.e., four 15 min intervals), computing the mean, maximum, minimum and range.
The two-level clustering algorithm was applied to both daily consumption and production data. We will present here the obtained results working with the daily consumption values.
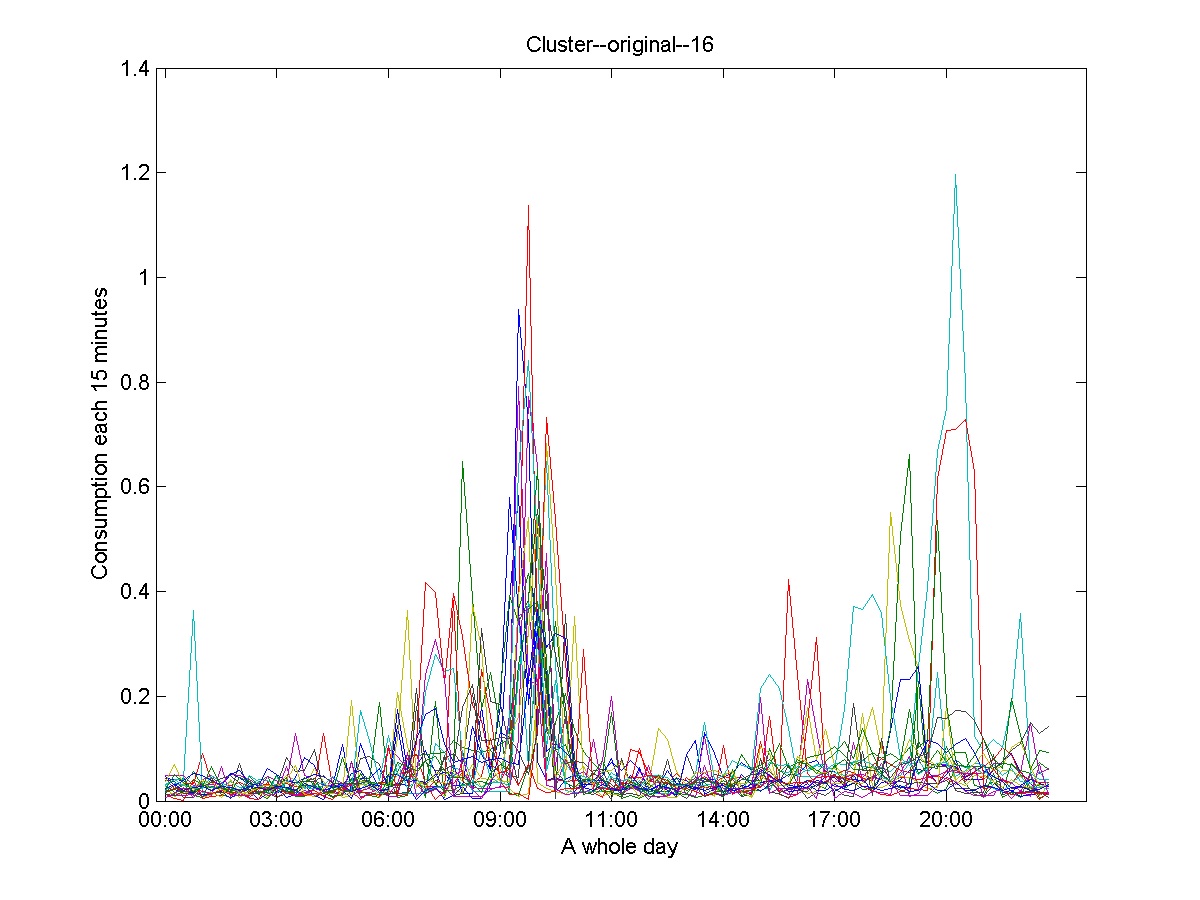 Figure 10
Cluster 16 from the first level
Figure 10
Cluster 16 from the first level
Source: Own elaboration.
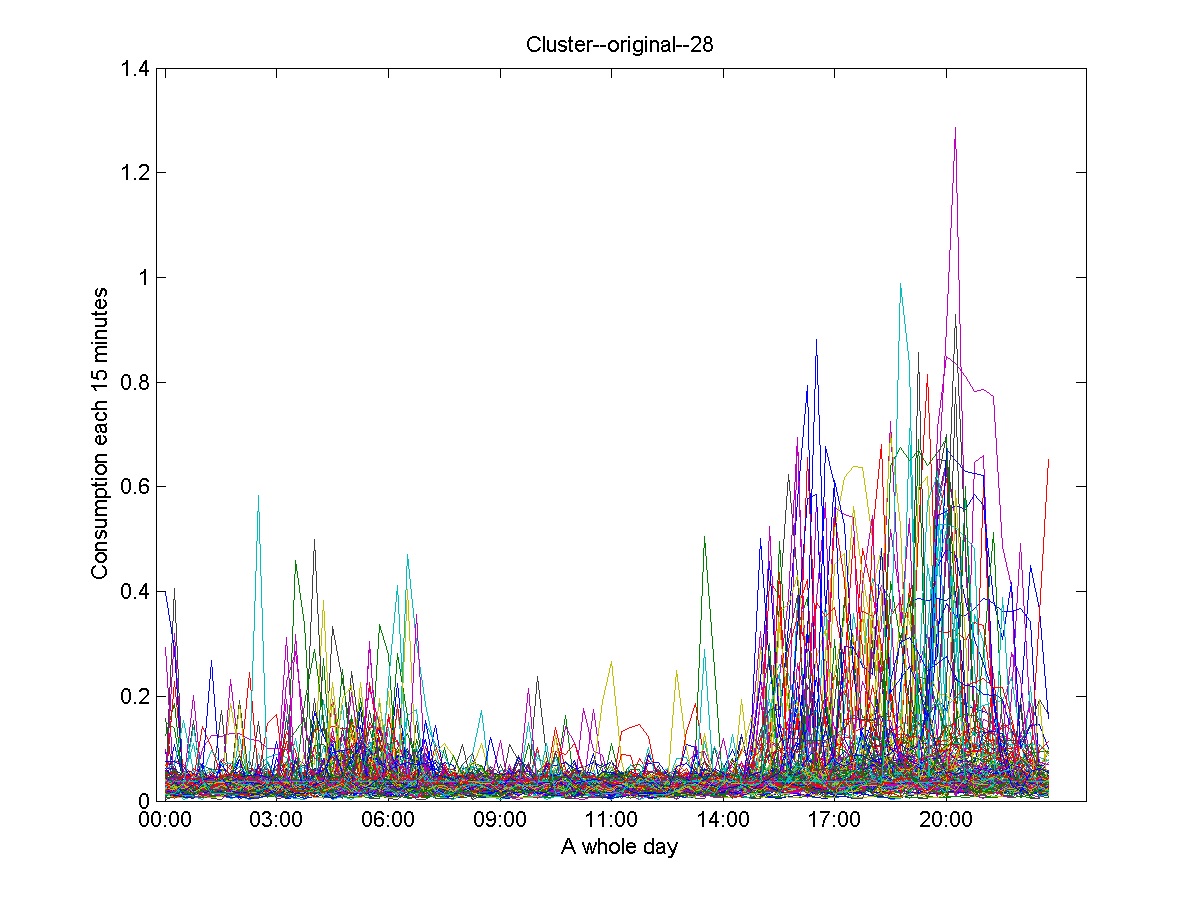 Figure 11
Cluster 28 from the first level
Figure 11
Cluster 28 from the first level
Source: Own elaboration.
Figures 10 and 11 show a selection of clusters obtained in the first level. These are the only two clusters from 38 obtained clusters in the first level, which express typical profiles only considering global features.
The clusters showed in Figure 12, Figure 13 and Figure 14 represent the clusters containing the majority of the time series. They illustrate the necessity of applying the second level for refining the clustering results and consequently obtain the daily consumption profiles.
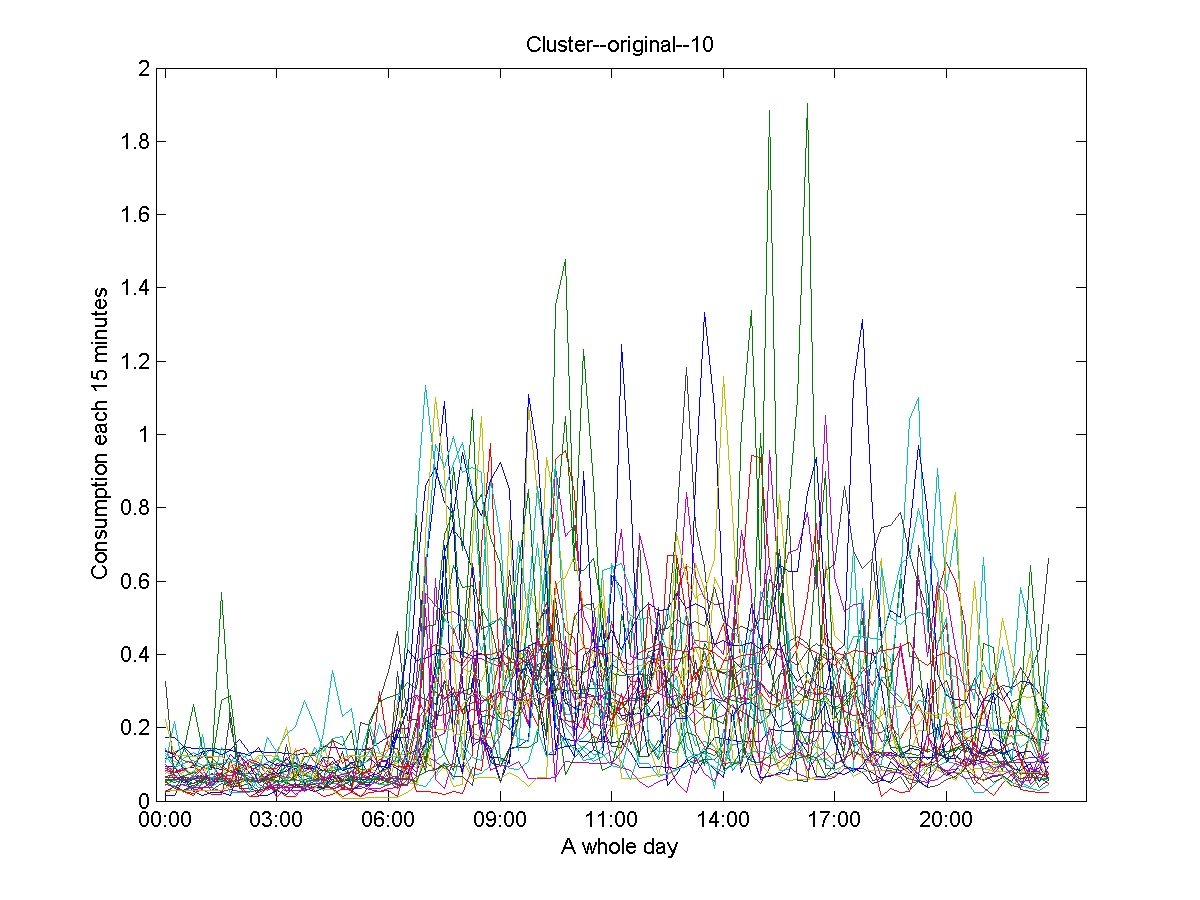 Figure 12
Cluster 10 from the first level
Figure 12
Cluster 10 from the first level
Source: Own elaboration.
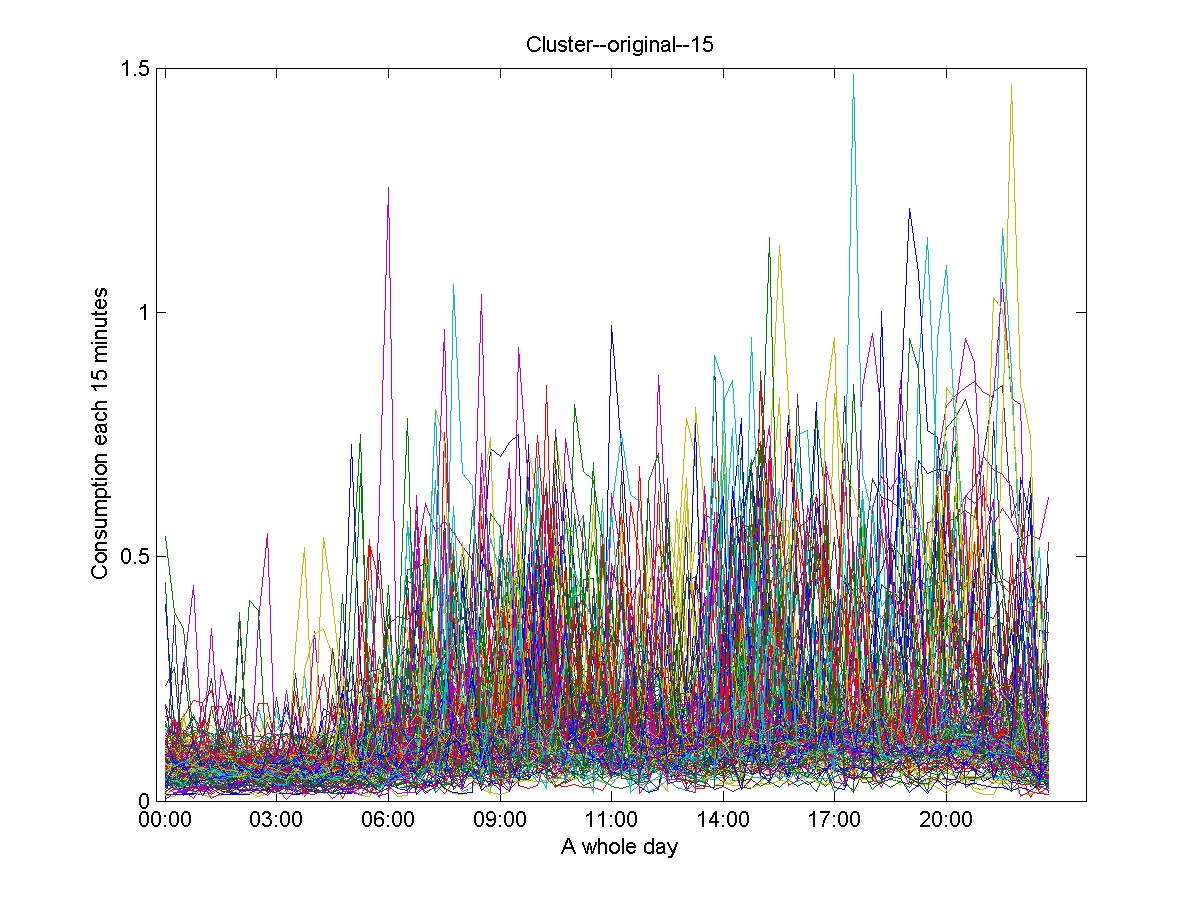 Figure 13
Cluster 15 from the first level
Figure 13
Cluster 15 from the first level
Source: Own elaboration.
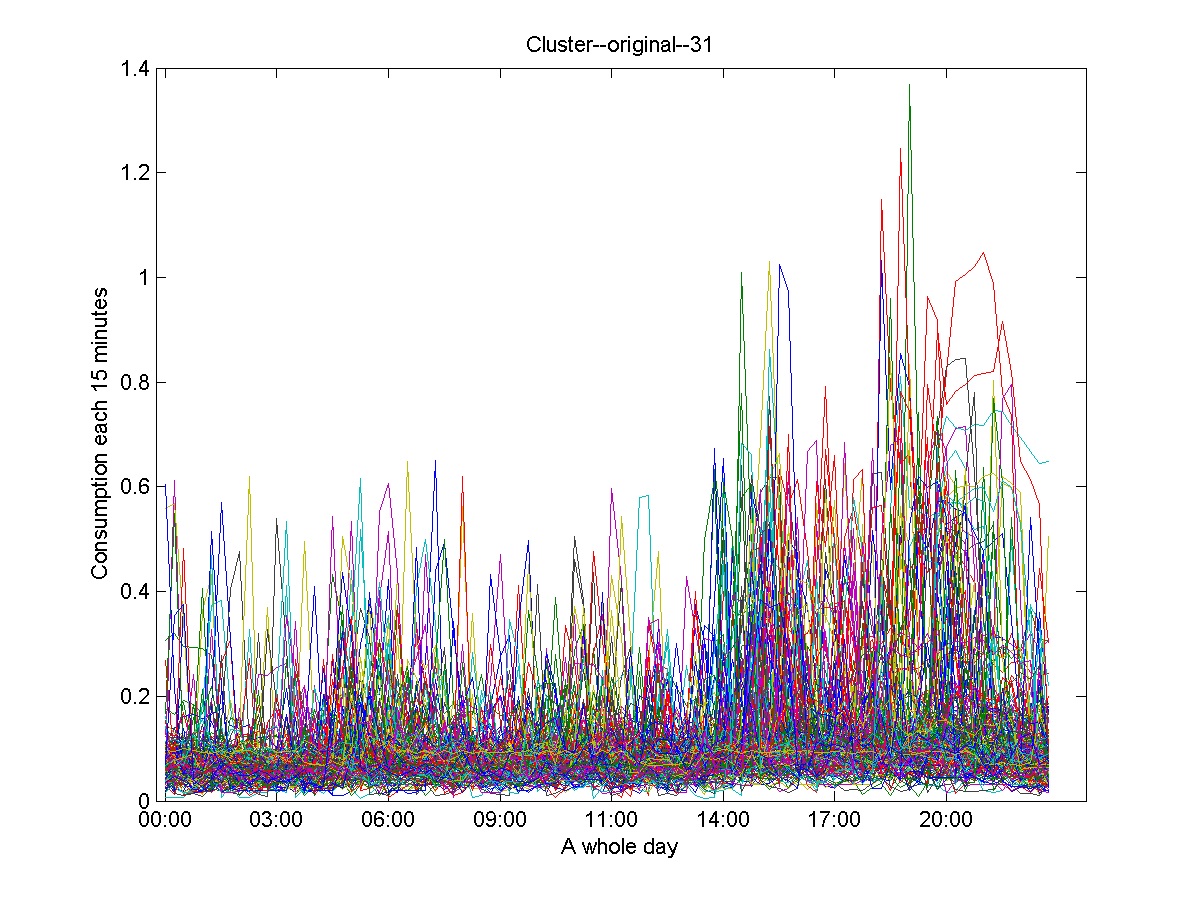 Figure 14
Cluster 31 from the first level
Figure 14
Cluster 31 from the first level
Source: Own elaboration.
After applying the second level, we really obtained the most representative daily consumption prototypes. We classified the most representative prototypes in the following categories: high, medium and low consumption prototypes. This classification is possible by only considering the first level results. Nevertheless, we refine this classification on the second level considering the consumption peaks and daily consumption behavior as we show in the following figures.
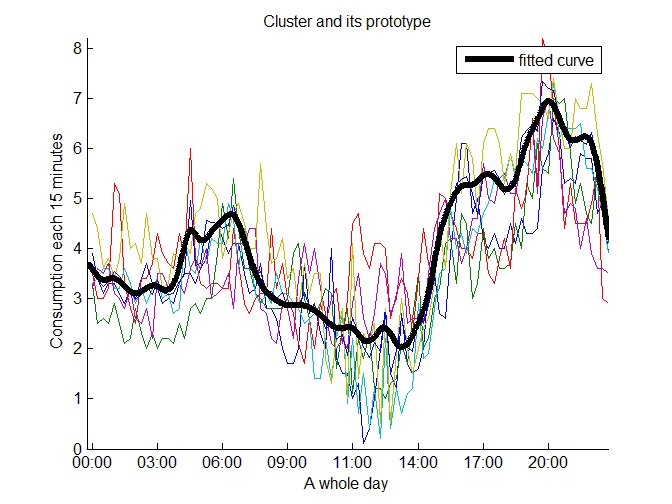 Figure 15
High daily consumption prototype
Figure 15
High daily consumption prototype
Source: Own elaboration.
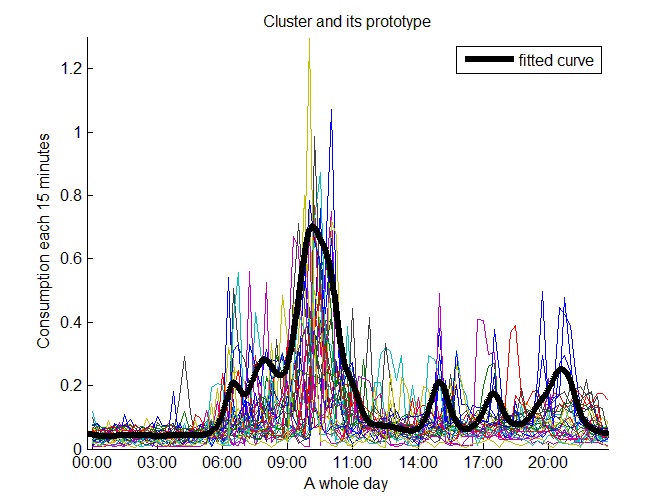 Figure 16
Medium consumption prototype with higher consumption in the morning
Figure 16
Medium consumption prototype with higher consumption in the morning
Source: Own elaboration.
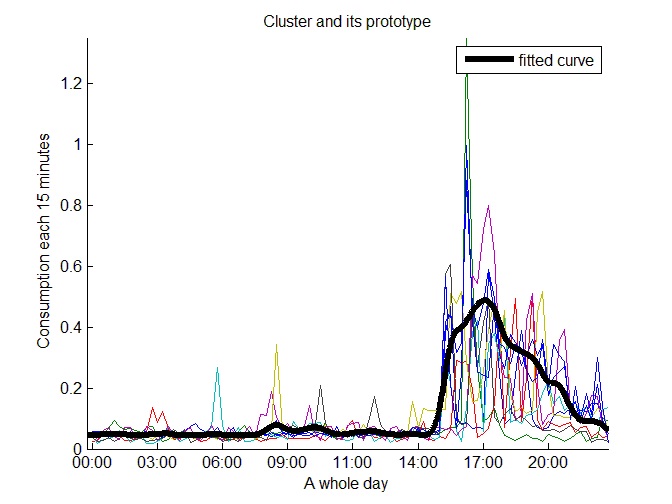 Figure 17
Medium consumption prototype with higher consumption in the afternoon
Figure 17
Medium consumption prototype with higher consumption in the afternoon
Source: Own elaboration.
We obtained six clusters that represent high consumption prototypes. Figure 15 shows one of them.
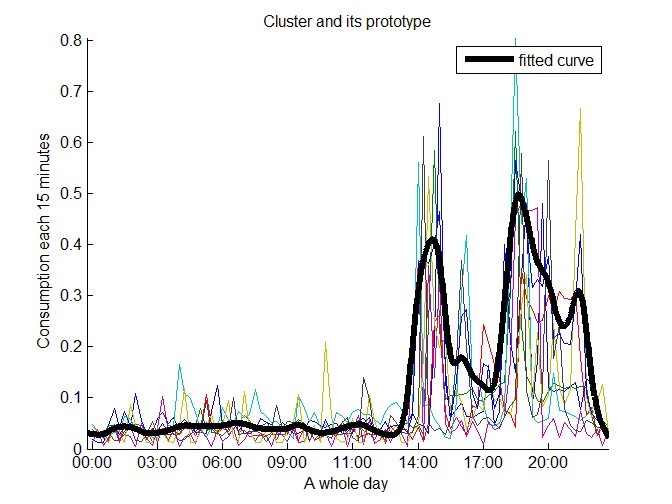 Figure 18
Medium consumption prototypes with higher consumption at afternoon-night
Figure 18
Medium consumption prototypes with higher consumption at afternoon-night
Source: Own elaboration.
Two clusters representing medium consumption prototypes with the higher consumption in the morning were obtained in the second level. Figure 16 shows one of them. Figure 17 shows one of the four obtained medium consumption prototypes with higher consumption in the afternoon; whereas Figure 18 shows one of the 10 detected medium consumption prototypes with consumption peaks at afternoon-night.
We identified four clusters that represent medium consumption prototypes with small consumption peaks in the morning and high consumption peaks in the afternoon, Figure 19 shows one of them.
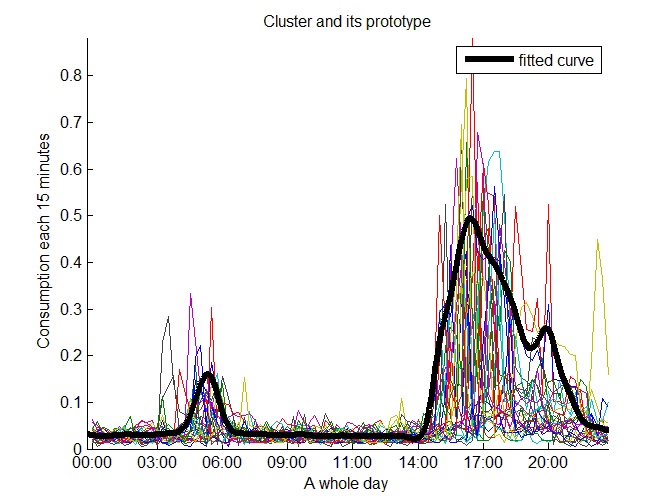 Figure 19
Medium consumption prototype with small consumption peaks in the morning and high consumption peaks in the afternoon
Figure 19
Medium consumption prototype with small consumption peaks in the morning and high consumption peaks in the afternoon
Source: Own elaboration.
Some consumers have a medium consumption from morning to afternoon, which is more or less constant. Figure 20 shows this kind of consumer.
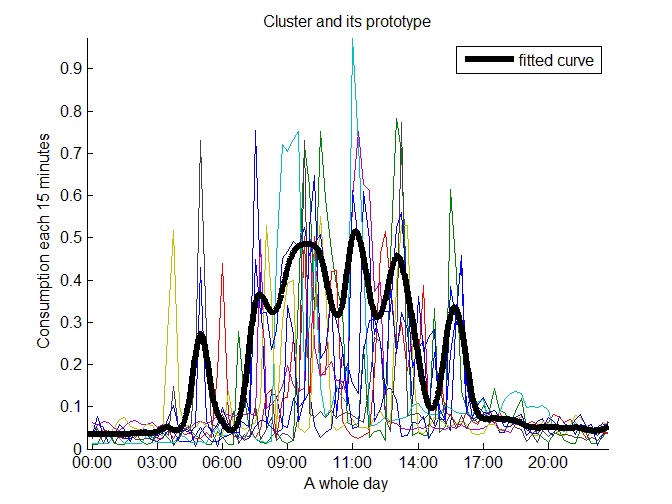 Figure 20
Typical consumption prototype with stable medium consumption from morning to afternoon
Figure 20
Typical consumption prototype with stable medium consumption from morning to afternoon
Source: Own elaboration.
The majority of the consumers have consumption peaks in the morning, in the afternoon and at night. Twelve typical medium consumption prototypes with these three peaks were found. Figure 21 shows one of them.
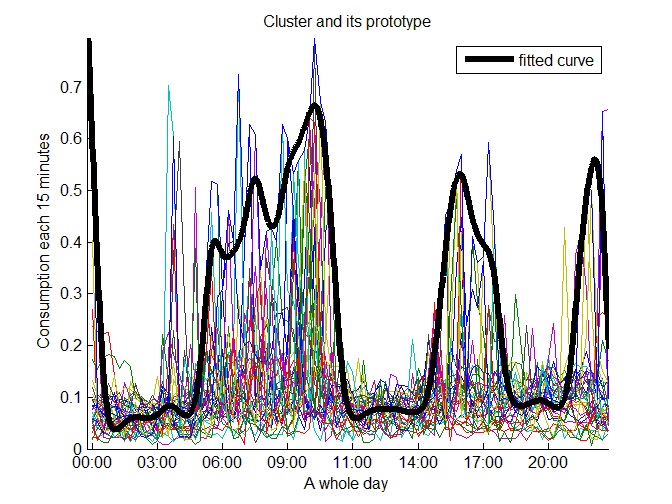 Figure 21
Typical medium consumption prototype with three consumption peaks in a day
Figure 21
Typical medium consumption prototype with three consumption peaks in a day
Source: Own elaboration.
Other consumers have a more variable consumption pattern because they have a lot of consumption peaks during the day. Figure 22 shows one of these kinds of daily consumption prototypes.
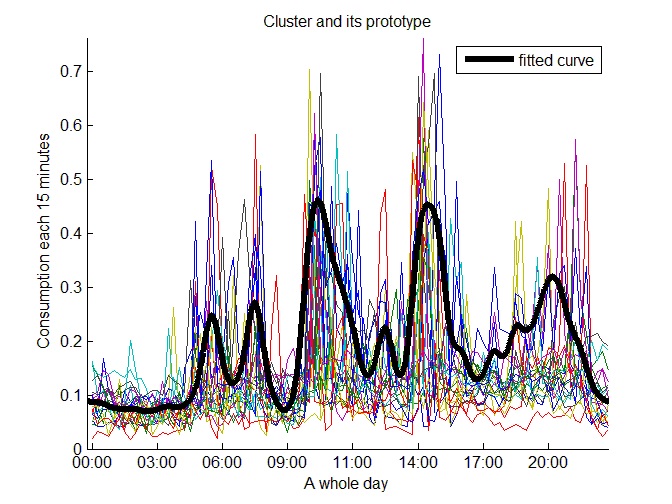 Figure 22
Typical medium consumption prototype with many consumption peaks in a day
Figure 22
Typical medium consumption prototype with many consumption peaks in a day
Source: Own elaboration.
We obtained two categories for grouping the low consumption prototypes, one of them with a stable consumption and the other one with peaks of consumption. Figure 23 and Figure 24 show representative clusters of these categories, respectively.
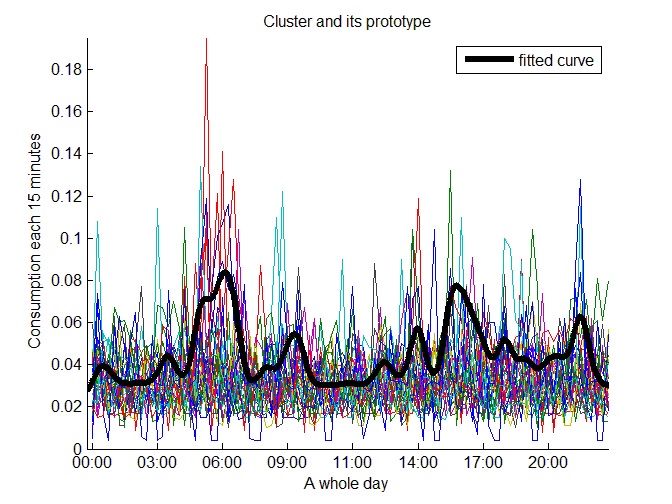 Figure 23
Low and stable consumption prototype
Figure 23
Low and stable consumption prototype
Source: Own elaboration.
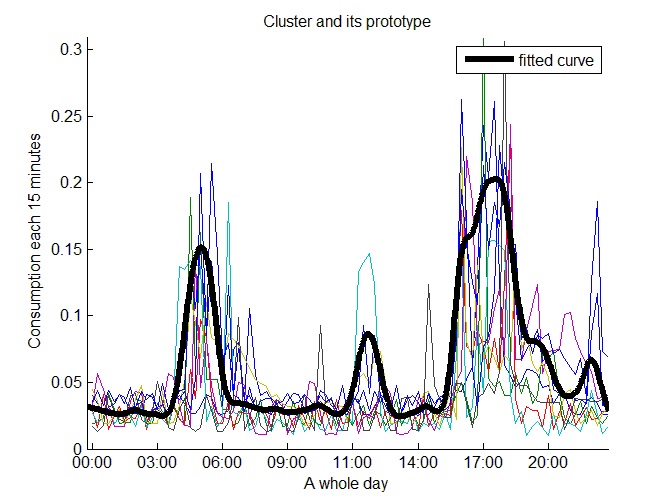 Figure 24
Low and unstable consumption prototype
Figure 24
Low and unstable consumption prototype
Source: Own elaboration.
The two-level clustering approach allows us to discover prototypes considering global consumption levels and consumption behaviors. We obtain clusters with homogeneous consumption levels in the first level and clusters with the same profile in the second level. However, two clusters obtained in the second level can look similar considering the consumption behavior, but they are very different taking into account the consumption levels. For instance, prototypes shown in Figure 25(a, b) have similar behavior but their general consumptions are different, between 0.05 kWh and 1.04 kWh in the top one, and between 0.00 kWh and 0.23 kWh for the bottom one.
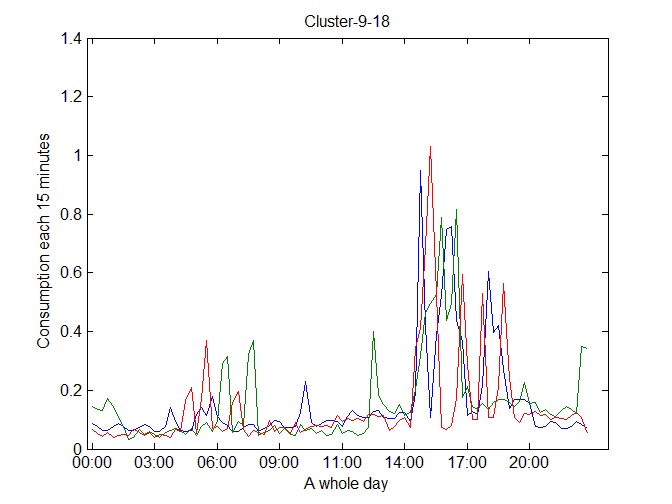 Figure 25a
Two clusters with similar profiles and different consumption levels
Figure 25a
Two clusters with similar profiles and different consumption levels
Source: Own elaboration.
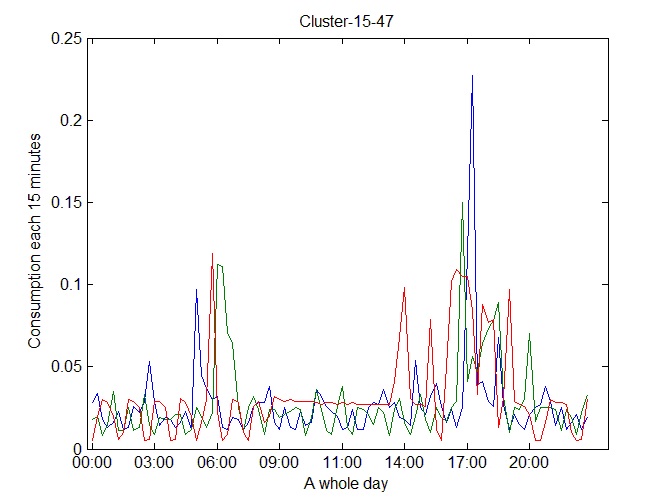 Figure 25b
Two clusters with similar profiles and different consumption levels
Figure 25b
Two clusters with similar profiles and different consumption levels
Source: Own elaboration.
Yearly consumption and production profiles
As we proceeded with the daily consumption and production data, we prepared two datasets for discovering yearly profiles. One with yearly consumption values and the other one with yearly production values. In both cases, each time series consists of 35040 energy consumption or production intervals, between 1st of November 2013 and 31st of October 2014. The global features were obtained by computing the mean, minimum, maximum, sum, median, variance, standard deviation and range considering the 35040 original features for each yearly consumption or production vector. For the second level, we created local features in order to refine the initial clustering results. In this case, the local features express the daily consumption or production, because we created eight features summarizing the information of each set of 96 consumption or production intervals by computing the mean, minimum, maximum, sum, median, standard deviation, variance and range statistics. Thus, we will not consider explicitly the daily consumption or productions behaviors.
The two-level clustering algorithm was applied to both yearly consumption and production matrices. Below we present the obtained results working with the yearly production values of 375 prosumers.
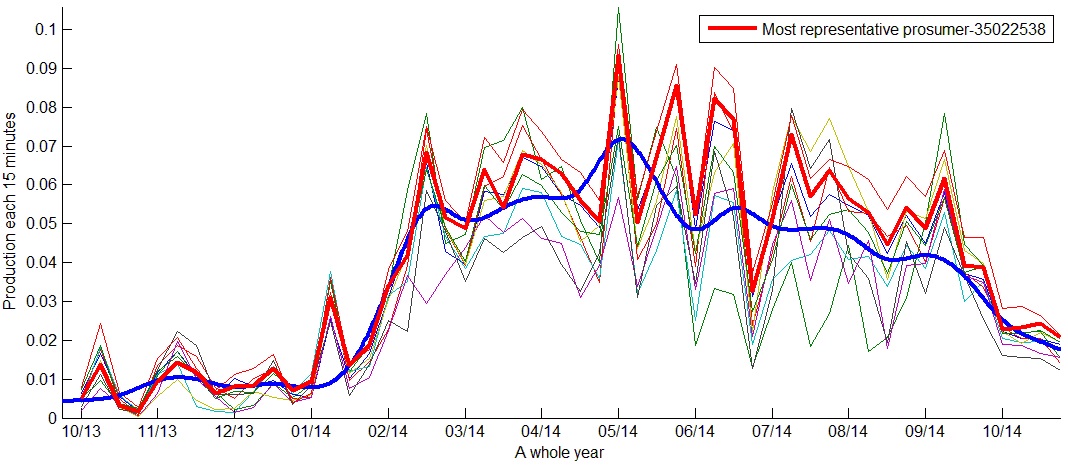 Figure 26
Yearly production profile and its most representative prosumer (35022538)
Figure 26
Yearly production profile and its most representative prosumer (35022538)
Source: Own elaboration.
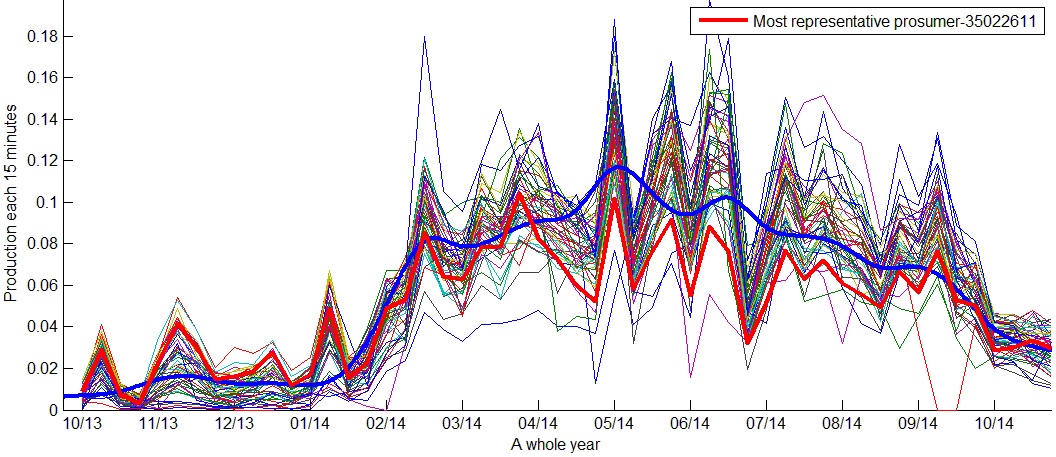 Figure 27
Yearly production profile and its most representative prosumer (35022611)
Figure 27
Yearly production profile and its most representative prosumer (35022611)
Source: Own elaboration.
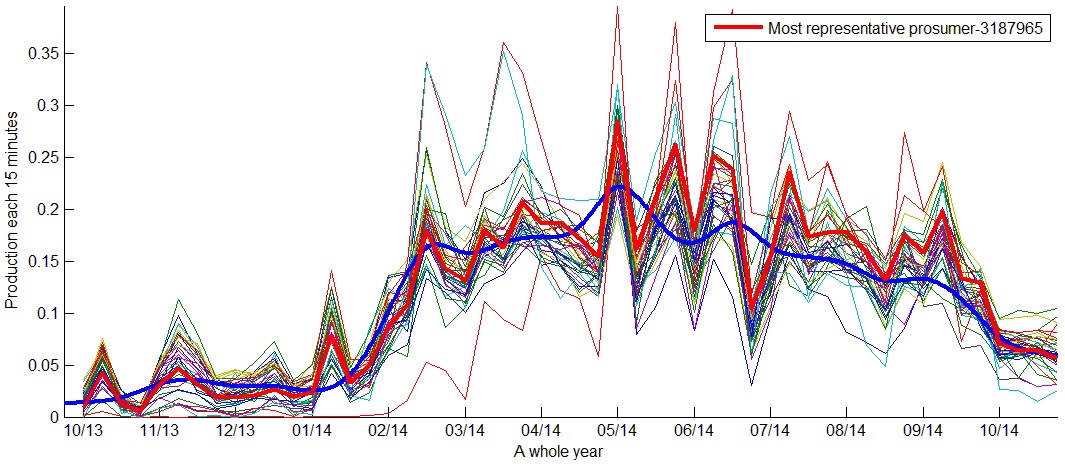 Figure 28
Yearly production profile and its most representative prosumer (3187965)
Figure 28
Yearly production profile and its most representative prosumer (3187965)
Source: Own elaboration.
As we can see in the following figures, the yearly production behavior is similar; nevertheless, we can see clusters with different production levels. Prosumers increase production between March and September. Figure 26 shows a cluster with the lowest yearly productions and Figure 27 shows a cluster with the highest yearly productions.
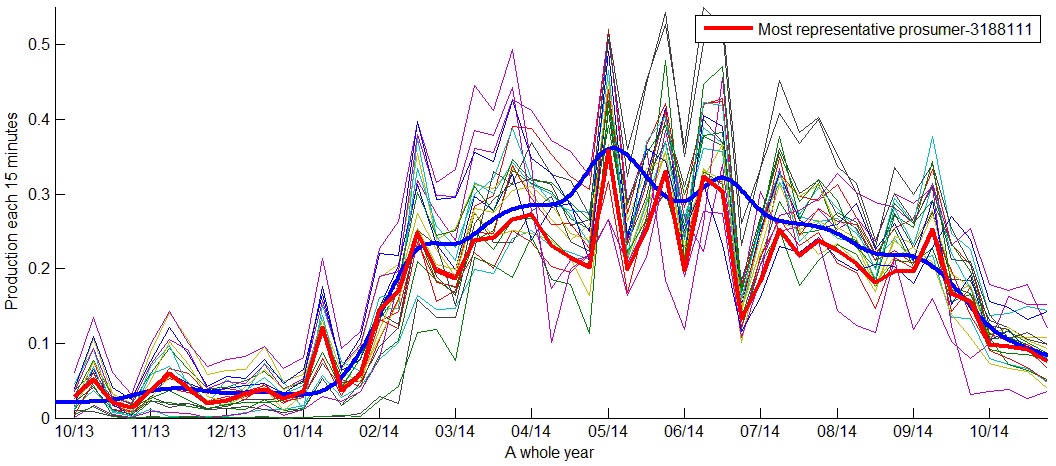 Figure 29
Yearly production profile and its most representative prosumer (3188111)
Figure 29
Yearly production profile and its most representative prosumer (3188111)
Source: Own elaboration.
Conclusions and future work
The proposed methodology was used through the application of the two-level clustering approach to Belgian energy consumption and production data. Daily consumption and production profiles were obtained, considering global features such as total daily consumption or production, and local features such as hourly consumption or production, respectively. Whereas, prototypical consumers and prosumers were discovered considering global features such as total yearly consumption or production, and local features such as daily consumption or production, respectively.
The proposed methodology has the following advantages. It allows obtaining different clustering results by using different time granules. Moreover, it allows considering different clustering objectives. In the first level, only some general statistics about the data are required; while in the second level, the main objective is the similarity in time for identifying the consumption or production profiles. The approach also allows for dimensionality reduction via feature extraction in the first level; doing so the clustering algorithm becomes more efficient. It extracts a set of measures from the original time series; as such it is possible to obtain good results using the Euclidean distance, whereas this measure cannot handle the original time series directly. It uses a finite set of statistical measures to capture the global and local nature of the time series; thus, the computational efficiency of the clustering algorithms can be improved and the use of more advanced clustering algorithms becomes possible. Finally, our approach allows obtaining clusters with homogeneous consumption or production levels in the first level and clusters with the same profile in the second level. We believe this latter characteristic is appealing to test decision policies as it is crucial that the situations are considered to consist of typical situations that might occur in reality.
Acknowledgement
The research we present in this paper was performed in the framework of the Erasmus Mundus Action 2 and in the context of the SCANERGY project. Erasmus Mundus Action 2, under the terms of the grant agreement number 2013-2591, EUREKA SD, finances a full time stay at the Postdoctoral level in the faculty of Sciences at Vrije Universiteit Brussel. SCANERGY project has received funding from the European Union's 7th Frame Program for research, technological development and demonstration under grant agreement number 324321.
References
Aghabozorgi, S., Saybani, M., & Wah, T. (2012). Incremental clustering of time-series by fuzzy clustering. Journal of Information Science and Engineering, 28, 671-688. https://www.iis.sinica.edu.tw/page/jise/2012/201207_03.pdf
Aghabozorgi, S., Ying Wah, T., Herawan, T., Jalab, H., Shaygan, M., & Jalali, A. (2014). A hybrid algorithm for clustering of time series data based on affinity search technique. Scientific World Journal, 2014, 1301-1314. https://doi.org/10.1155/2014/562194
Ahmad, T., Chen, H., Wang, J., & Guo, Y. (2018). Review of various modeling techniques for the detection of electricity theft in smart grid environment. Renewable & Sustainable Energy Review, 82(August), 2916-2933. https://doi.org/10.1016/j.rser.2017.10.040
Albert, A., & Rajagopal, R. (2013). Smart meter driven segmentation: What your consumption says about you. IEEE Transaction. Power Systems, 28, 4019-4030. https://doi.org/10.1109/TPWRS.2013.2266122
Alzate, C., Espinoza, M., De Moor, B., & Suykens, J. (2009). Identifying customer profiles in power load time series using spectral clustering. Artificial Neural Networks – ICANN, 2009, LNCS 5769, 315-324. https://doi.org/10.1007/978-3-642-04277-5_32
Ardakanian, O., Koochakzadeh, N., Singh, R., Golab, L., & Keshav, S. (2014). Computing electricity consumption profiles from household smart meter data. In EDBT Workshop on Energy Data Management (pp. 140-147). https://pdfs.semanticscholar.org/11b9/5c1d7861e7932919394f65487b551ab3e1cd.pdf
Binh, P., Ha, N., Tuan, T., & Khoa, L. (2010). Determination of representative load curve based on Fuzzy K-Means. 4th International Power Engineering and Optimization Conference (PEOCO), Shah Alam, pp. 281-286. https://doi.org/10.1109/PEOCO.2010.5559257
Brockwell, P., & Davis, R. (2002). Introduction to time series and forecasting, 2 ed. Springer Texts in Statistics. New York: Springer Verlag.
Cao, H., Beckel, C., & Staake, T. (2013). Are domestic load profiles stable over time? An attempt to identify target households for demand side management campaigns, in 39th Annual Conference of the IEEE Industrial Electronics Society (pp. 4733-4738). IECON. https://doi.org/10.1109/IECON.2013.6699900
Capozzoli, A., Piscitelli, M., Brandi, S., Grassi, D., & Chicco, G. (2018). Automated load pattern learning and anomaly detection for enhancing energy management in smart buildings. Energy, 157, 336-352. https://doi.org/10.1016/j.energy.2018.05.127
Chicco, G. (2012). Overview and performance assessment of the clustering methods for electrical load pattern grouping. Energy, 42(1), 68-80. DOI: 10.1016/j.energy.2011.12.031
Defays, D. (1977). An efficient algorithm for a complete link method. The Computer Journal, 20(4), 364-366. https://doi.org/10.1093/comjnl/20.4.364.
Dent, I., Aickelin, U., & Rodden, T. (2011). Application of a clustering framework to UK domestic electricity data. Ukci, 161-166. https://arxiv.org/abs/1307.1079
Espinoza, M., Joye, C., Belmans, R., & DeMoor, B. (2005). Short-Term load forecasting, profile identification, and customer segmentation: A methodology based on periodic time series. IEEE Transaction. Power Systems, 20(3), 1622-1630. https://doi.org/10.1109/TPWRS.2005.852123
European Commission. (2014). Benchmarking smart metering deployment in the EU-27 with a focus on electricity. Reports. Publications Office of the European Union https://ses.jrc.ec.europa.eu/publications/reports/benchmarking-smart-metering-deployment-eu-27-focus-electricity
Fenza, G., Gallo, M., & Loia, V. (2019). Drift-aware methodology for anomaly detection in smart grid. IEEE Access, 7, 9645-9657. https://doi.org/10.1109/ACCESS.2019.2891315
Figueiredo, V., Rodrigues, F. Vale, Z., & Gouveia, J. (2005). An electric energy consumer characterization framework based on data mining techniques. IEEE Transaction. Power Systems, 20(2), 596-602. https://doi.org/10.1109/TPWRS.2005.846234
Flath, C., Nicolay, D., Conte, T., Van Dinther, C., & Filipova-Neumann, L. (2012). Cluster analysis of smart metering data: An implementation in practice. Business & Information Systems Engineering, 4, 31-39. https://doi.org/10.1007/s12599-011-0201-5
Funde, N., Dhabu, M., Paramasivam, A., & Deshpande, P. (2019). Motif-based association rule mining and clustering technique for determining energy usage patterns for smart meter data. Sustainable Cities Society, 46(January), 101415. https://doi.org/10.1016/j.scs.2018.12.043
Giordano, V., Gangale, F., Fulli, G., & Sánchez, M. (2011). Smart grids projects in Europe: Lessons learned and current developments. Federal Energy Regulatory Commission. https://ses.jrc.ec.europa.eu/sites/ses/files/documents/smart_grid_projects_in_europe.pdf
Hossain, J., Kabir, A., Rahman, M., Kabir, B., & Islam, R. (2011). Determination of typical load profile of consumers using fuzzy c-means clustering algorithm. Int. J. Soft Comput. Eng., .(5), 169-173. https://es.scribd.com/document/349605721/Determination-of-Typical-Load-Profile-of-Consumers-Using-Fuzzy-C-Means-Clustering-Algorithm
Hübner, M., & Prüggler, N. (2011). Smart grids initiatives in Europe - Country snapshots and country fact sheets. JRC Reference Reports. Austrian Energy Agency. https://ses.jrc.ec.europa.eu/sites/ses/files/documents/smart_grid_projects_in_europe.pdf
Iglesias, F., & Kastner, W. (2013). Analysis of similarity measures in times series clustering for the discovery of building energy patterns. Energies, 6, 579-597. https://doi.org/10.3390/en6020579
Kohonen, T. (1982). Self-organized formation of topologically correct feature maps. Biol. Cybern., 43(1), 59-69. https://doi.org/10.1007/BF00337288
Lai, C.-P., Chung, P.-C., & Tseng, V. S. (2010). A novel two-level clustering method for time series data analysis. Expert Systems with Applications, 37(9), 6319-6326. https://doi.org/10.1016/j.eswa.2010.02.089
Lavin, A., & Klabjan, D. (2014). Clustering time ‐ series energy data from smart meters. Energy Efficiency, 8(4), 1-9. https://doi.org/10.1007/s12053-014-9316-0
Lee, T., Haben, S., & Grindrod, P. (2014). Modelling the electricity consumption of small to medium enterprises. In The 18th European Conference on Mathematics for Industry Conference (pp. 1-7). Taormina, Italy: ECMI.
Losa, I., De Nigris, M., & Van, T. (2013). Analysis of the on-going research and demonstration efforts on smart grids in Europe, 22nd International Conference on Electricity Distribution, June, 10-13. https://doi.org/10.1049/cp.2013.0958
MacQueen, J. (1967). Some methods for classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium Mathematical Statistics and Probability, 1, 281-297.
McLoughlin, F., Duffy, A., & Conlon, M. (2012). Analysing domestic electricity smart metering data using self organising maps. In CIRED 2012 Workshop: Integration of Renewables into the Distribution Grid, pp. 319-319. https://doi.org/10.1049/cp.2012.0865
Mutanen, A., Ruska, M., Repo, S., & Järventausta, P. (2011). Customer classification and load profiling method for distribution systems. IEEE Trans. Power Deliv., 26, 1755-1763. https://doi.org/10.1109/TPWRD.2011.2142198
Nanopoulos, A., Alcock, R., & Manolopoulos, Y. (2001). Feature-based classification of time-series data. International Journal of Computer Research, 10, 49-61. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.73.9555
Oates, T., Firoiu, L., & Cohen, P. (1999). Clustering time series with hidden Markov Models and dynamic time warping. In Proceedings of the IJCAI-99 Workshop on Neural, symbolic and reinforcement learning methods for sequence learning (pp. 17-21).
Räsänen, T., & Kolehmainen, M. (2009). Feature-based clustering for electricity use time series data. In 9th International Conference, ICANNGA 2009, LNCS 5495, 401-412. https://doi.org/10.1007/978-3-642-04921-7_41
Räsänen, T., Voukantsis, D., Niska, H., Karatzas, K., & Kolehmainen, M. (2010). Data-based method for creating electricity use load profiles using large amount of customer-specific hourly measured electricity use data. Appl. Energy, 87, 3538-3545. https://doi.org/10.1016/j.apenergy.2010.05.015
Renner, S., & Heinemann, C. (2011). European Smart Metering Landscape Report, 2(February), 168 p. https://www.sintef.no/globalassets/project/smartregions/d2.1_european-smart-metering-landscape-report_final.pdf
Shi, J., & Malik, J. (2000). Normalized cuts and image segmentation. IEEE Trans. Pattern Anal. Mach. Intell., 22(8), 888-905. https://doi.org/10.1109/34.868688
Wang, X., Smith, K., & Hyndman, R. (2006). Characteristic-based clustering for time series data. Data Min. Knowl. Discov., 13, 335-364. https://doi.org/10.1007/s10618-005-0039-x
Wang, X., Smith, K., Hyndman, R., & Alahakoon, D. (2004). A scalable method for time series clustering. Research of Monash University. Victoria, Australia: Monash University. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.155.207
Warren Liao, T. (2007). A clustering procedure for exploratory mining of vector time series. Pattern Recognit., 40, 2550-2562. https://doi.org/10.1016/j.patcog.2007.01.005
Zhang, X., Liu, J., Du, Y., & Lv, T. (2011). A novel clustering method on time series data. Expert Systems Applications, 38, 11891-11900. https://doi.org/10.1016/j.eswa.2011.03.081
Notes
*
Research paper
Author notes
a Corresponding author. E-mail: larcogar@vub.be
Additional information
How to cite: Arco G., L., Casas C., G. M., & Nowé A. (2020). Two-level clustering methodology for smart metering data. Cuadernos de Administración, 33. https://doi.org/10.11144.Javeriana.cao33.tlcms