Introduction
Databases often show outliers observations, which present a different behavior from the majority. It is important to detect these observations since they affect the data analysis in different ways. In this respect, Uriel Jiménez and Aldás Manzano (2005) point out:
-
They could mask the data pattern and distort the results, so the conclusions would be completely different without their presence.
-
They could affect the normality condition that is necessary in many multivariate techniques.
Outliers have different causes:
-
Measurement errors, collection or transcription.
-
Intentional errors of response from the respondents.
-
Sampling errors: the incorporation of sample statistical units from different populations to the target population.
-
Intrinsic heterogeneity: the observed elements belong to the target population, but the inherent variability of the samples differs from the rest in their choices, attitudes or behavior.
Sometimes the detection of outliers is the first step in statistical analysis. Other times, the outliers need to be removed or downweighted; different causes motivate different procedures. The detection of outliers depends on the type of error (or cause) in the data. In the case of errors in measurement or data entry to the base, it is relatively simple to correct them and it is convenient to eliminate the obvious mistakes. However, a controversial question is: What should we do when the outliers derive from the intrinsic heterogeneity of the data?
In this paper we discuss some multivariate methods for detecting outliers. In multivariate methods, there exist two approaches to identify outliers: those based on the distances of the observations in the data center and those projecting the original data. The projection pursuit methods easily identify atypical observations, and they have the advantage that it is not necessary to know the data distribution. However, the disadvantage of the projection pursuit methods is that there are high requirements in terms of computational load, which increments significantly when there is an increase in the variables considered.
The document is organized as follows. The first section describes two algorithms used to detect outliers (Filzmoser et al., 2008; Peña & Prieto, 2001) based on projection pursuit. The second section compares the methods developed applying them in a group of Argentine companies that listed their shares publicly in the period 2004-2012. In final section, we developed the main conclusions, and we describe research limitations and future research work related to this topic.
Algorithms’ Description
Mahalanobis’ distance from the center of the data is the classical multivariate way of identifying outliers observations far from most others.
Let x
1, x
2...x
n be a random sample from a normal multivariate distribution
Np
(µ,Σ) where µ is the multivariate location vector and Σ the p x p covariance matrix. The distance between the i-th observation xi and the location µ, weighted by the covariance Σ is using to detect if the observation xi is an outlier, it is (1).
The square Mahalanobis distance has Chi-square distribution with p degrees of freedom and the observation . is consider outlier if  (by setting the squared Mahalanobis distance equal to certain quantile of Chi-squared distribution it is possible define ellipsoids having the same Mahalanobis distance from the data centre).
(by setting the squared Mahalanobis distance equal to certain quantile of Chi-squared distribution it is possible define ellipsoids having the same Mahalanobis distance from the data centre).
When both µ and Σ are unknown it be used estimators, i.e. the vector mean  and sample covariance matrix S, to estimate the Mahalanobis distance
and sample covariance matrix S, to estimate the Mahalanobis distance  ,see (2):
,see (2):
The vector mean and the covariance matrix are affected by outliers, besides the Mahalanobis distance relies on the assumption of normality. Therefore, it is affected by outliers and it does not allow identify sets of outliers (Peña, 2002).
An alternative approach is to use robust location and scale estimators, measures resistance against the influence of outlying observations. Maronna (1976) studied affinely equivariant M-estimators for covariance matrices, and Campbell (1980) proposed using the Mahalanobis distance computed using M-estimators for the mean and covariance matrix.
Nevertheless, the distance method approach presents two difficulties: (i) obtaining a reliable robust location estimator, and (ii) determining and classifying the outliers. It is important to find metric separating outliers from regular observations. Rousseeuw (1985) proposed other distance-based algorithm that computes the ellipsoid with the smallest volume or with the smallest covariance determinant that would include at least half of the data points (minimum covariance determinant, MCD). Because these procedures are based on the minimization of certain nonconvex and nondifferentiable criteria, these estimators are computed by resampling.
Rousseeuw and Driessen (1999) get faster algorithm splitting the problem into smaller subproblems (FAST-MCD algorithm).
Others outlier-detection procedures are basing on projections to identify outliers. The underlying motive of these methods is to find suitable projection of the data in which the outliers are readily apparent and can thus be downweighted to yield a robust estimator.
Gnanadesikan and Kettenring (1972) proposed to search for outliers in the direction of the first principal components: the direction of the maximum variability of the data. Although this method provides a correct solution when the outliers are located close to the directions of the principal components, it may fail to identify outliers in the general case.
From that point of view, Stahel (1981) carry on projection pursuit on the data using random directions. They proposed to compute the weight for the robust estimators from the projections of the data onto some directions. These directions were chosen maximizing distances based on robust location and scale estimators, and the optimal values for the distances could also be used to weight each point in the computation of the robust covariance matrix. Stahel (1981) developed a computer approximation based on direction from random subsamples.
Rousseeuw (1993) proposed selecting . observations from the original sample and computing the orthogonal direction of the hyperplane defined by these observations. The maximum over this finite set of directions is used as an approximation to the exact solution.
The disadvantage of the projection pursuit methods is the form to increase the computational burden with the variable number.
Peña and Prieto (2001) proposed an improve examining only the set of 2. directions that maximize or minimize the kurtosis. A small number of outliers would cause heavy tails and lead to a larger kurtosis coefficient while a large number of outliers would start introducing bimodality and decrease the kurtosis coefficient (Filzmoser et al., 2008).
Projection pursuit methods have a computational time that increase very rapidly in higher dimensions.
Principal components are those orthogonality directions that maximize the variance along each component. It is well-known the method of dimension reduction that seems intuitive to identifying outliers since outliers increase the variance along their respective directions. The outliers appear more visible in principal components space, at least in some direction of maximum variance, than the original data space. Principal components select a small quantity of highly informative components, discarding those are not contribute significant additional information. In this way, the dataset become more computationally tractable without losing a lot of information. Filzmoser et al. (2008) proposed a method based on the principal components properties useful to detect outliers in high dimensions.
In the following sections, we describe the Peña and Prieto (2001) and Filzmoser et al. (2008) methods.
Kurtosis method (Kurt) (Peña & Prieto, 2001)
Given a sample (x1,....xn) of a p-dimensional random variable X the algorithm consists in projecting each observation onto a set of 2p directions, which are obtained as the solutions of 2p simple smooth optimization problems.
1) The original data are rescaled and centred, see (3).
Where  and S
x are the mean and sample variance, respectively.
and S
x are the mean and sample variance, respectively.
2) Set  the iteration index j compute p orthogonal directions that maximize the kurtosis coefficient obtained as a solution of the following optimization problem (4).
the iteration index j compute p orthogonal directions that maximize the kurtosis coefficient obtained as a solution of the following optimization problem (4).
3) Project sample points onto a lower dimension subspace (p – j), orthogonal to the direction dj. Define (5):
Where ej
denotes the first unit vector, I the identity matrix and Qj
is orthogonal. Compute the new values in (6),
Where  is the first component of
is the first component of  which satisfies
which satisfies  (the univariate projection values) and
(the univariate projection values) and  corresponds to the remaining p- j components of
corresponds to the remaining p- j components of  .
.
4) Compute j’ = j+1 and repeat (2) y (3) up to have p directions: d1, d2, …, dp
.
5) Repeat (2) and (3) computing p orthogonal directions that minimize the kurtosis coefficient (idem step 2) obtaining dp+1, dp+2, dp+1, ...,d2p
.
6) To determine an outlier in any one of the 2p directions  , we compute a univariate measure rescaling with the median (med) and the median absolute deviation (MAD), see (7).
, we compute a univariate measure rescaling with the median (med) and the median absolute deviation (MAD), see (7).
Where β is a cut-off chosen to ensure a reasonable level of Type I error and depend on the sample space dimension p. See Table 1.
Table 1

Source: Own elaboration.
7) Define a new sample composed of all observations i if  , and the procedure is applied again to the reduced sample. This is repeated until either no additional observations satisfy
, and the procedure is applied again to the reduced sample. This is repeated until either no additional observations satisfy  or the number or remaining would be less than [(n+p+1)/2].
or the number or remaining would be less than [(n+p+1)/2].
8) Let U denote the set of all observations not labelled as outliers and computed the mean vector  , the covariance matrix
, the covariance matrix  ; and Mahalanobis distance:
; and Mahalanobis distance:  .
.
Those observations  such that
such that  are considered not be outliers and included in U. The procedure is repeated until U becomes the set of all observations.
are considered not be outliers and included in U. The procedure is repeated until U becomes the set of all observations.
The Kurtosis method is affine equivariant. Peña and Prieto (2001) conclude after several computational experiments to study the practical behaviour of the proposed procedure, that it shows a satisfactory empirical performance, especially for large sample space dimensions and concentrated contaminations.
However other authors discussed the Kurtosis method, they argue important points. The method works well in the presence of scattered outliers or multiple clusters of outliers.
For those cases in which the shape of the contamination is similar to that of the original data, the method can be supplement with other general methods (an alternative approach is to use clustering methods to supplement the general-purpose robust methods). The greatest chance of success comes from use of multiple methods, at least one of which is a general-purpose method such as FAST-MCD and MULTOUT, and at least one of which is meant for clustered outliers, such as Kurt method.
However, several key aspects of the Kurt algorithm proposed are criticized. The standardization in Step 1 uses the classical mean and covariance matrix. It is well known that these estimators are extremely sensitive to outliers, which often leads to labelling outliers as good data points and good points as outliers. The authors answer:
This problem cannot appear in our method. First, note that the algorithm we propose is affine equivariant, independently of the initial standardization. The kurtosis coefficient is invariant to translations and scaling of the data and a rotation will not affect the maximizes or minimisers. Moreover, we have tried to be careful when defining the operations to generate the successive directions, as well as in the choice of an initial direction for the optimization problems. (Peña & Prieto, 2001, p. 307)
Maximizing and minimizing the kurtosis in Steps 2 and 3. The authors indicates that the kurtosis is maximal (respectively, minimal) in the direction of the outliers when the contamination is concentrated and small (respectively, large). However, this is not always true for an intermediate level of contamination. The authors answer:
The behaviour of the kurtosis coefficient is particularly useful to reveal the presence of outliers in the cases of small and large contaminations, and this agrees with the standard interpretation of the kurtosis coefficient as measuring both the presence of outliers and the bimodality of the distribution. What is remarkable is that in intermediate cases with a=0.3 the procedure does not break down completely and its performance improves with the sample size. (Peña & Prieto, 2001, p. 307)
Taking 2p orthogonal directions in Steps 2 and 3, the chosen directions are still rather arbitrary. Which is the reason to consider the only first p directions that maximize the kurtosis and then p directions that minimize the kurtosis? Why it not proposed to alternate between directions using a procedure that stops once a significant direction is computed? The authors argue “The algorithm we describe does not make use of this feature, and in this sense it is a simpler one to describe and understand, although it may be more expensive to implement” (Peña & Prieto, 2001, p. 307).
Regarding the choice of orthogonal directions, they reply:
Our motivation to use these orthogonal directions is twofold. On the one hand, we wish the algorithm to be able to identify contamination patterns that have more than one cluster of outliers. The second motivation arises from a property of the kurtosis that implies that in some cases the directions of interest are those orthogonal to the maximization or minimization directions. (Peña & Prieto, 2001, p. 307)
The authors did not explain how they obtained the cut-off values β
p in Table 2 to choice in Step 7. The response:
The results are unfortunately not totally satisfactory; the reason is the large variability in these values in the simulations[1]. This variability has two main effects –it is difficult to find correct values (huge numbers of replications would be required) and for any set of 100 replications there is a high probability that the resulting values will be far from the expected one. Nevertheless, we agree that these values could be estimated with greater detail, although they do not seem to be very significant for the behaviour of the algorithm, except for contaminations very close to the original sample. (Peña & Prieto, 2001, p. 308)
Sequential determination of outliers in Step 8, the mean and covariance matrix of the good data points are computed and used to decide which outliers can still be reclassified as good observations. This procedure is repeated until no more outliers can be reallocated. It has suggested that Step 8 be applied only once. The authors are a little surprised by the criticism of procedures that determine the outliers sequentially. They replied:
The statistical literature is full of examples of very successful sequential procedures and, to indicate just one, Peña and Yohai (1999) presented a sequential procedure for outlier detection in large regression problems that performs much better than other nonsequential procedures. (Peña & Prieto, 2001, p. 309)
Method PCOut (Filzmoser et al., 2008)
This algorithm was designed primarily for computational efficiency at high dimension. It consists in two steps: The first one to detect the location outliers and the second one to detect scatter outliers.
1) Rescale the data X(n,p)
using the median (med) and the median absolute deviation (MAD), see (8):
Compute the covariance matrix from X*
.
2) Compute the eigenvalues and eigenvectors from covariance matrix X*
, a semirobust principal component decomposition, and retain only p* eigenvectors whit eigenvalues that represent the 99% of the variance. The matrix of principal components is Z: Z=X*V. where V is the matrix of eigenvalues p* × p*. Z is rescaled by the median and the MAD as 8), for i-th component, see (9):
Z*, principal components rescaled is stored for the both phases of the algorithm.
Phase 1: Location outliers.
3) Compute a robust kurtosis weights for each component denoted by wj
in (10).
Peña and Prieto (2001) argue in the Kurt method, both small and large values of the kurtosis coefficient can be indicated of outliers. In order to use relative weights is defined .
To classify the data between outliers and non-outliers we need to determinate a weighted norm from transformated data Z* but it has not chi quadratic distribution. Z* is similar as a robust Mahalanobis distance (RDi) (distance from median rescaled by MAD). Therefore, the algorithm used a robust distance transform similar Maronna and Zamar (2012), that helped the empirical distances di to have the same median to the theoretical distance and bring the former somewhat closer . See (11):
4) To assign weights to each observation and use it as a measure of outlyingness is calculated the translated bi-weight function w1i (Rocke, 1996), see (12):
Where M is equal to 33⅓ quantil of the distances and c, see (13):
Phase 2: Scatter outliers.
5) Use the step 2 decomposition and calculate the Euclidean norm for the data in non-weighting principal component space (equivalent to the Mahalanobis distance in the original data but faster to compute). After use the Maronna and Zamar (2012) transformation, the distances set is going to use at 6.
6) Determine the weights w2i to each robust distance with the translated biweight function where c2 is equal to , M2 is equal to and finally we calculate the final weight, see (14):
Where typically the scaling constant s = 0.25. Outliers are then classified as points they have weight wi < 0.25. This value implies that if one of the weights equals one the other must be less than 0.0625. If w1 = w2, x is classified as outlier when the common value is less than 0.375.
The computational speed that is the speed t of the computer to process data[2] is an advantage of this algorithm. Using examples an simulated data Filzmoser et al. (2008) infer that PCOut is a competitive outlier detection algorithm regarding detection accuracy as well as computation time.
The comparison with methods in low dimension, using simulated data reveals that PCOut performs well at identifying outliers, with low masked outliers, although it has a higher percent non-outliers that were classified as outliers. It does particularly well for location outliers while Kurt does very poorly, however Kurt does exceptionally well for scatter outliers.
An empirical application
In this paper we applied the detection outliers methods to a sample composed by a set of Argentine companies that quote their shares in the Buenos Aires stock exchange in the period 2004-2012. The database was prepared relying on the data publicly available in the Buenos Aires stock exchange web site (Bolsar, s.f.) including only companies that presented a positive operative ordinary income defined as net sales larger that costs of sales and selling and administrative expenses, and excluding those that belong to the financial and insurance sectors. A total of 744 observations (firms per year) belonging to 111 firms were considered.
The variables used to detect outliers are the following financial reporting indicators to analyse cost-effectiveness and cost behaviour (Anderson, Banker, & Janakiraman, 2003; Banker & Byzalov, 2014).
-
Market to book value. The ratio of indicates investors’ expectations of future abnormal earnings relative to assets in place. It reflects both the magnitude and persistence of sales growth expectations.
-
Current Assets and non-current Assets
-
Operating income. It is equals all revenue from the property minus all reasonably necessary operating expenses.
-
Net Revenues. A company’s revenue net of discounts and returns.
-
Net Revenues annual variation coeff. The annual change in a company's net income.
-
Selling Administrative expenses
[3]. It is the sum of direct, indirect selling expenses and administrative expenses of a company.
-
Selling Administrative expenses. Annual variation coeff.
The Table 2 and Figure 1 summarize a preliminary descriptive analysis of original sample. The univariate statistical analysis (descriptive measures and boxplots) shows the skewness and outliers.
Table 2

Source: Own elaboration.
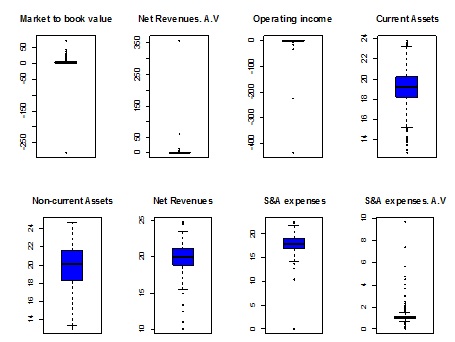 Figure 1
Boxplot of original variables
Figure 1
Boxplot of original variables
Source: Own elaboration.
We detected outliers using Mahalanobis distance and the both projection pursuit methods presented by Peña and Prieto (2001) and Filzmoser et al. (2008) denominated Kurt and PCOut, respectively. In this work we compare the results defining finally as outliers all the outliers defined using both methods proposed.
We used the Matlab for the Kurt method and the R package mvoutlier for the PCOut method (Filzmoser, 2015).
The Table 3 shows the outliers detected by differences algorithms. There were detected 48 outliers (6.5% of the data) by the distance methods (Mahalanobis). By using projection pursuit methods a large outliers were detected. 212 (28.5%) by Kurt method and 203 (27.3%) by PCOut of outliers. The algorithms proposed detected a similar quantity. Nevertheless the 69.8% of Kurt outliers were PCOut outliers (see Table 4).
Table 3
Outliers detected
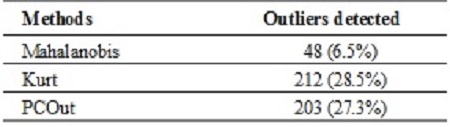
Source: Own elaboration.
Table 4
Outliers detected comparing methods
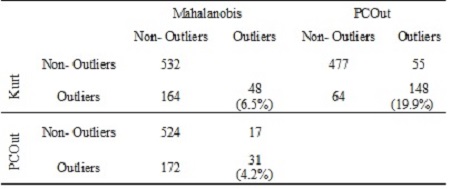
Source: Own elaboration.
The biplots (Figure 2) shows the detected outliers using different methods in the space of the first and second principal component.
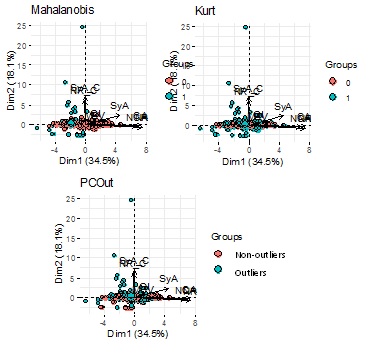 Figure 2
Biplot showing outliers identified by Methods
Figure 2
Biplot showing outliers identified by Methods
Source: Own elaboration.
For each method it has been calculated the first and second principal components of the non-outliers data and graphic it on biplots which shows different structures of the data (See figure 3).
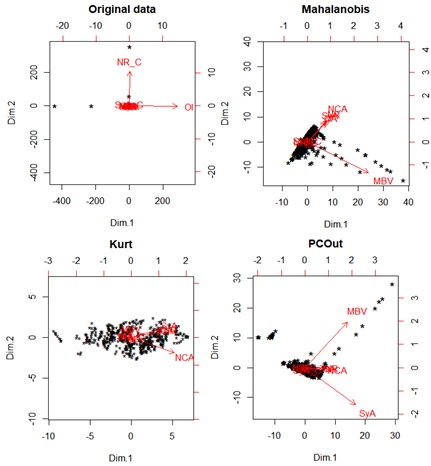 Figure 3
Biplot without outliers by Method
Figure 3
Biplot without outliers by Method
Source: Own elaboration.
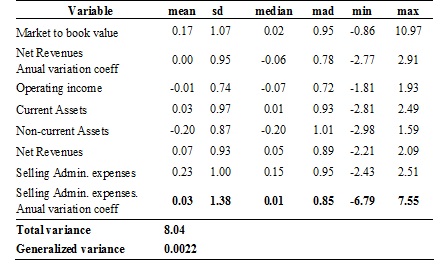
Table 5 shows descriptive measures of the variables considered in non-outliers database, the mean vector difference, the multivariate variability (total and generalized variance) by method. Multivariate variances are significantly lower in all cases because of excluding outliers distorting the estimates.
Table 5
Multivariate descriptive without outliers
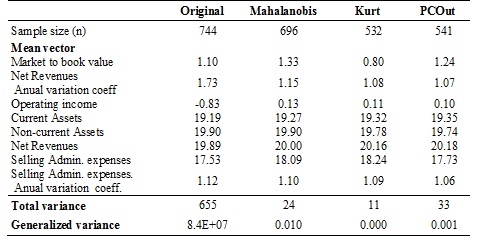
Source: Own elaboration.
A plausible criterion for determining multivariate outliers is to use different methods and consider as those who are simultaneously identified as atypical by them. Particularly, in this application 19.9% of the data were identified as outliers at Kurt and PCOut methods.
The different results and different performance of each method leads us to consider all the outliers detected for these methods. We aggregated the outliers identified by all the methods taking advantage of their performance. I this empirical application, we detected 225 outliers (30.24%). Figure 4 shows in the space of the two first principal components of the sample all the outliers detected for the algorithms.
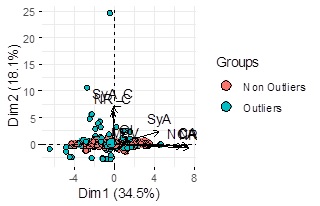 Figure 4
Outliers detected by all algorithms
Figure 4
Outliers detected by all algorithms
Source: Own elaboration.
The biplot without the outliers detected by all the methods (Figure 5) shows a better performance. Besides we pointed with a circle a set of data that we could study especially because they presented a different behaviour.
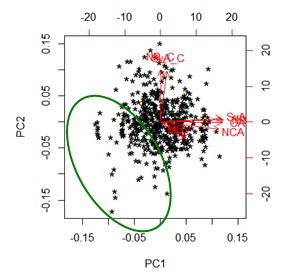 Figure 5
Biplot without all the Outliers detected
Figure 5
Biplot without all the Outliers detected
Source: Own elaboration.
Table 6 and Figure 6 show a descriptive analysis of data without all the Outliers detected. The variables exhibited less skewness and heterogeneity, resulting a data sample more homogeneous.
Table 6
Multivariate descriptive without all the Outliers detected
Source: Own elaboration.
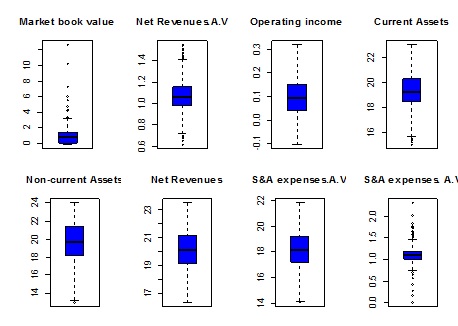 Figure 6
Boxplott without all the Outliers detected
Figure 6
Boxplott without all the Outliers detected
Source: Own elaboration.
Conclusions
Outliers distort the results and mask the real data structure, so to detect them is an important task in the multivariate data analysis.
This work presented two pursuit algorithms to detect outliers, they are an example of the different algorithms available. But is not possible to point one algorithm as the better, it depends of the data sample and the algorithms could show similar performance. Each one method has some disadvantage, so we proposed aggregate the outliers detected by different methods (in this paper Kurt and PCOut methods) and use their different performance to improve the outliers detection. Specially the projection pursuit methods that they only search the useful projections, they are not affecting by non-normality and can be widely applied in diverse data situations.
A multivariate outliers detection is important for thorough data analysis, however, the researchers have to decide to exclude the outliers from further analysis or apply robust procedures to reduce the impact of them.


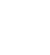
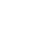



 (1)
(1) (by setting the squared Mahalanobis distance equal to certain quantile of Chi-squared distribution it is possible define ellipsoids having the same Mahalanobis distance from the data centre).
(by setting the squared Mahalanobis distance equal to certain quantile of Chi-squared distribution it is possible define ellipsoids having the same Mahalanobis distance from the data centre). and sample covariance matrix
and sample covariance matrix  ,see (
,see ( (2)
(2) (3)
(3) and
and  the iteration index
the iteration index  (4)
(4) (5)
(5) (6)
(6) is the first component of
is the first component of  which satisfies
which satisfies  (the univariate projection values) and
(the univariate projection values) and  corresponds to the remaining
corresponds to the remaining  .
. , we compute a univariate measure rescaling with the median (
, we compute a univariate measure rescaling with the median ( (7)
(7)
 , and the procedure is applied again to the reduced sample. This is repeated until either no additional observations satisfy
, and the procedure is applied again to the reduced sample. This is repeated until either no additional observations satisfy  or the number or remaining would be less than [
or the number or remaining would be less than [ , the covariance matrix
, the covariance matrix  ; and Mahalanobis distance:
; and Mahalanobis distance:  .
. such that
such that  are considered not be outliers and included in
are considered not be outliers and included in  (8)
(8) (9)
(9) (10)
(10)
 (12)
(12) (13)
(13) (14)
(14)










