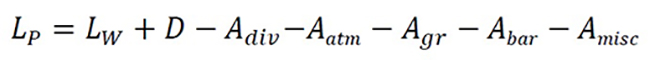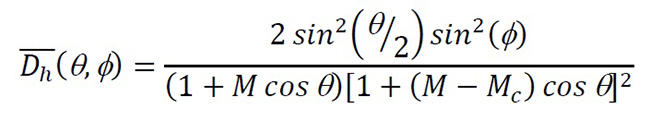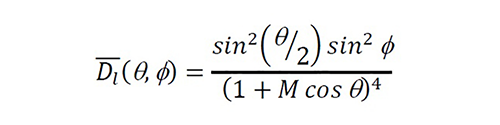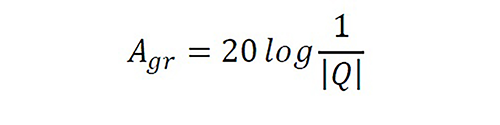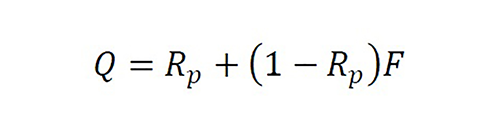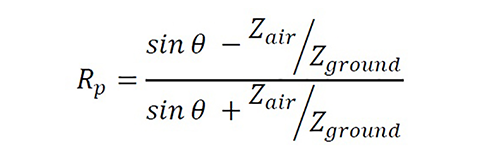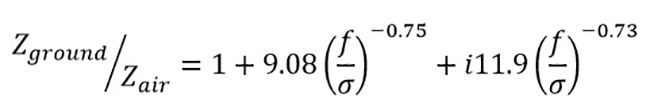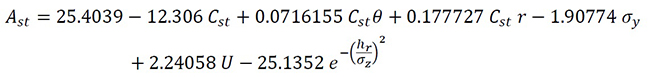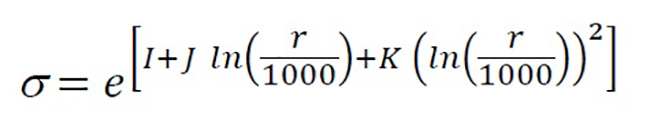Introduction
According to a poll conducted by P.E. Mediterranean Acoustics Research & Development (PEMARD) at the end of 2011, members of the Acoustics Institute (IOA) and the Acoustical Society of America (ASA) were asked about which outdoor sound propagation method or model they use more often. Of the thirty-eight responses, 71 % still prefer the ISO 9613 method. This standard is an empirical method that has many limitations and yields results that are inaccurate and imprecise [1].
According to P. Economou and P. Charalampous, the weakest parts of the implementation of this method are the flexibility of the method and that uneven ground cannot be properly modeled. Calculations are carried out in octave bands, and sound energy calculations remove interference effects, just to mention a few. Bearing in mind its lack of accuracy and its crude model representation, one wonders why it is still the preferred method [1].
As stated by Wondollek, according to the ground attenuation equations of the model from standard ISO 9613 Part 2, soil attenuation should be approximately 0 dB for porous soil above 125 Hz. Accordingly, porous soil would produce a ground attenuation equal to zero, whereas hard soil would result in reinforcement. Another fact that must be taken into account is that the source height has no influence on the ground effect when it is greater than 10 m, and the ground effect is independent of the average size of the area [2].
International standard ISO 9613 Part 2 specifies an engineering method for calculating sound attenuation during outdoor propagation to predict sound pressure levels at certain distances from various sources [3]. In this method the source of noise emission is considered a point source, and sound emission at any receiver is predicted with reasonable accuracy under conditions that are favorable for the propagation of sound [4].
The model can be used for estimating noise levels using a specific receptor for common sources of noise emission in relatively simple environments, such as when the distances separating the source from the receptor are relatively small and when there are no intervening structures that impede the noise propagation. That is, when there is direct propagation. However, the level of uncertainty that still exists in the prediction of noise levels using current analytical and empirical models can be significant. Therefore, a good model for noise propagation that considers the effects of weather conditions is necessary to accurately predict noise levels generated by fixed sources.
The method of ISO 9613 Part 2 predicts sound pressure level during outdoor propagation under weather conditions that are favorable for the propagation of emitted noise [5]. These conditions are summarized as follows:
- The wind blows from the source to the receptor within an angle of ±45º in a direction that connects the center of the dominant sound source with the center of the reception area being considered.
- The speed of the wind is 1-5 m/s (measured from an altitude of between 3 and 11 m from the ground surface).
- Well-developed, moderate thermal inversion conditions that as commonly occur on calm, cloudless nights.
The downwind equivalent continuous sound pressure levels in octave bands at a specific receptor a certain distance from a source may be calculated using the equation 1[5]:
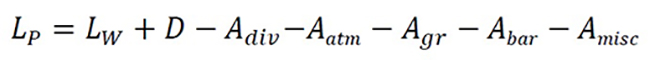 Equation 1
Equation 1
where
Lp
= Sound pressure level in octave bands at a specific receptor, dB(A)
Lw= Level of sound power in octave bands produced by a sound point source, dB(A)
D= Directionality factor, dB(A)
Adiv
= Attenuation due to geometrical divergence, dB(A)
Aatm= Attenuation due to atmospheric absorption, dB(A)
Agr= Attenuation due to the ground effect, dB(A)
Abar= Attenuation due to a barrier, dB(A)
Amisc= Attenuation due to miscellaneous other effects, dB(A)
General methods for calculating Adiv, Agr, and Abar are specified in ISO 9613 Part 2. Information on three contributions to the last term (the attenuation due to propagation through foliage, industrial sites and housing areas) is given in annex A of ISO 9613 Part 2. The continuous downwind sound pressure levels obtained with equation 1 are for each octave band.
Due to the wide range of uses of the noise prediction model and the numerous factors that influence sound pressure levels in open field, no procedure exists for defining a detailed model that would be adequate for each specific application [6].
Atmospheric stability strongly affects the vertical profile of wind and the force of turbulence in the atmosphere [7]. Variations in temperature influence air density and, consequently, in the velocity of sound wave propagation.
Recently, some studies that have begun to consider the influence of atmospheric stability on sound propagation have been reported [7] and [8]. Atmospheric conditions play a dominant role in the sound pressure level caused by a given noise emission source at a particular location and time. Different prediction models have different ways of considering atmospheric conditions. Standard ISO 9613 Part 2 considers propagation conditions to be simultaneously downwind in all directions (i.e., the model favors sound propagation from a source to any receptor to a certain degree) during a moderate thermal inversion. However, it does not consider the absolute worst-case scenarios in the environment, so it is possible that the actual impact exceeds the predicted impact [8].
The effects of weather conditions on the propagation of the sound are not significant over short distances, but for larger distances, weather conditions become more relevant as the respective heights of the source and the receptor increase [5].
Materials and Methods
In this study, an experimental program was designed to test the accuracy of the predictive method proposed by standard ISO 9613. This included measuring sound pressure levels in free field conditions under given weather conditions at various distances from a noise emission source and comparing them against the estimated sound pressure levels by standard ISO 9613 Part 2. The residual values serve as an input to develop and propose an improved model. There were no acoustic barriers.
The readings were performed on the Medellin University grounds, in the sports arena, alternating between the synthetic soccer field and the adjacent parking lot. The readings were obtained when classes were not being conducted to avoid movement throughout the entire sports area and additional noise sources. Different sites were selected for taking the readings, all of which were downwind from the noise emission source.
To simulate noise from various types of industrial activities or from emission sources that are typical of a city with characteristics like those of Medellin, previously recorded tracks on an iPod were played on a Bose speaker placed at a height of 30 cm above the ground.
An experimental design was made to select the sample size. Sixty-three (63) measurements were made at different distances from the speaker to appreciate the gradual decrease in sound pressure levels. The sound pressure levels in the octave bands at each of the measurement points were measured simultaneously with weather variables that allowed the authors to determine the class of the atmospheric stability, including the wind speed, cloud cover, solar incidence angle, ambient temperature and relative humidity. Both values were averaged over a period of 10 min. The sound pressure levels were registered and measured with a Casella CEL 633C class 1 sound level meter with the microphone placed at an altitude of 1.2 m above ground level; this was repeated at various distances (ranging from 2 m to 64 m) downwind from the speaker, as prescribed in standard ISO 1996 [9].
The procedure that was employed to measure the power levels of the sound in an open field from the values of the sound pressure level measured in the near vicinity was stipulated by standard ISO 3744 [10].
The final step consisted of analyzing the effects of the atmospheric stability on the noise propagation originating from a fixed noise source. Adjusting the prediction model to the experimental data led to improvements of the model. This model was then used to predict sound pressure levels at a specific receiver at some distance from the noise source for a wide range of weather conditions. The prediction model chosen for this study was based on the one proposed in standard ISO 9613 because it covers the principal sound pressure attenuation mechanisms, although these may be improved.
A detailed statistical analysis was performed using the data obtained in the field to study the dependence of the residual sound pressure level with the remaining parameters that were observed (the independent variables) during the measurements.
The statistics software Statgraphics Centurion XVI version 16.1.11 (Statpoint Technologies, Inc) was used to analyze the data and obtain the mathematical model. The variables that were inserted into the mathematical model were selected through the statistical software XLSTAT 2009.1.02 (Addinsoft) using principal component analysis. The variables that exhibited a correlation with the residual sound pressure level (either positive or negative and from highest to lowest) were introduced one by one into the mathematical model until an equation was obtained which explained the differences between the measured sound pressure levels and their estimated values.
Using the data obtained from the measurements and comparing them with the estimated levels, a calculation procedure was developed to predict the noise emanating from a noise source. The calculation method includes the parameters that generally affect sound pressure levels. The adjusted model shows the dependence that exists between the attenuation due to the atmospheric stability and the remaining independent variables.
To determine how to simplify the model, the highest p-value was considered for the independent variables. If the p-value was lower than 0.05, it can be noted that a statistically significant relationship exists between the variables in a 95 % confidence level. Therefore, no variable should be removed from the model. The R2 statistic indicates the percentage to which the model explains the variability of the dependent variable. The standard error of the estimation may be used to construct prediction limits for new observations.
This analysis presents an equation for the adjusted model for attenuation due to atmospheric stability. The data were processed to determine the correlations between the residual sound pressure level, wind speed, atmospheric stability, distance, and incidence angle.
For this purpose, a multiple regression was conducted to analyze the correlations between the measured data in which the dependent variable is the residual sound pressure level given by the method established by standard ISO 9613 Part 2, with the following adjustments:
Directionality Factor
The equations for sound directionality proposed by Brooks, Pope, and Marcolini [11], [12] and [13] are used in this study. These equations are the same as those expressed by Hoogzaad [14], wherein the sound directionality depends on not only the position of the receptor with respect to the noise emission source but also the wind speed.
For high frequencies (≥ 1000 Hz), the sound directionality factor is expressed by the equation 2[11], [12] and [13]:
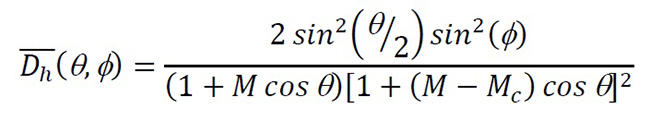 Equation 2
Equation 2
where M is the Mach number from the supporting surface in motion, Mc (Mc = 0.8 M) is the number of convective Mach based on the flow at the trailing edge, and θ and Ø are the angles of directionality, as shown in figure 1.
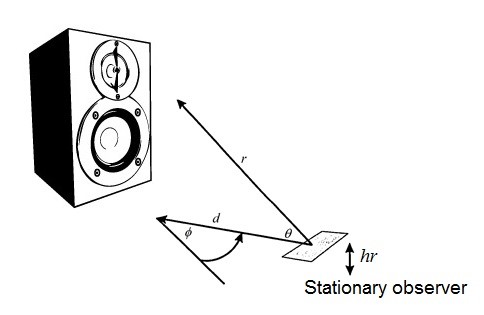 Figura1
Figure 1. Angles used in the directionality factors
Figura1
Figure 1. Angles used in the directionality factors
The sound directionality factor for low frequencies (< 1000 Hz) is expressed by the equation 3 [11] and [15]:
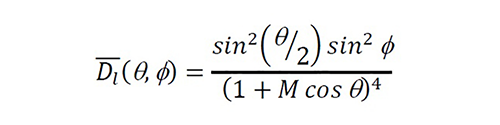 Equation 3
Equation 3
Attenuation due to Ground Effects
The propagation of sound near the ground depends on the impedance level of the surface [16]. Porous surfaces allow sound to penetrate and therefore to be absorbed, submitting it to a phase change through friction and thermal exchanges [4].
Ground attenuation is calculated using the spherical reflection coefficient of the sound wave, as shown in the equation 4[17]:
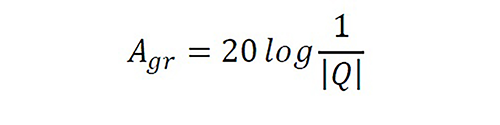 Equation 4
Equation 4
The spherical reflection coefficient is related to the reflection coefficient of the plane wave Rp
by means of the equation 5 [17]:
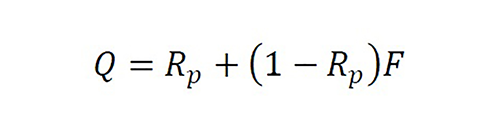 Equation 5
Equation 5
where F is the coefficient of loss at the interaction boundary between the front of the wave and the finite impedance surface, which is a function of the distance, the ground impedance, and the angle of incidence.
When the angle of incidence is greater than 5º, F → 0, which indicates that the orb shape of the front of the wave need not be considered [18]. The plane wave reflection coefficient is determined from the equation 6[17]:
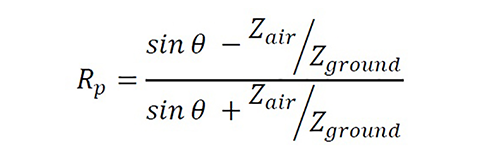 Equation 6
Equation 6
where
θ= Angle of incidence of the sound wave, °
Zair
= Characteristic impedance of air at 20 °C (415 Ns/m3)
Zground
= Complex impedance of the ground, Ns/m3
Various approximations have been formulated to determine ground impedance [17]. The Delany-Bazley model is characterized by its simplicity since it requires only one parameter, i.e., the flow resistivity. It is an empirical model based on a regression analysis of acoustic properties and the resistivity of air flows at the ground surface [19] (equation 7):
 Equation 7
Equation 7
where
f= Frequency, Hz
σ= Resistivity of air flows at the ground surface, g/(s∙cm2)
Typical values for air flow resistivity at the ground surface for different types of surfaces are shown in table 1.
Table 1. Resistivity of airflow at the ground surface for different types of ground surfaces
Source: Lamancusa[20]
Attenuation due to Effects of Atmospheric Stability
The atmospheric stability significantly affects the vertical wind profile and the atmospheric turbulence [7]. Variations in temperature influence the density of air and, consequently, the velocity of propagating sound waves.
The model proposed for attenuation due to effects of atmospheric stability is given by the equation 8:
 Equation 8
Equation 8
where
C
st= Class of atmospheric stability
σ
z
= Vertical propagation coefficient, m
σ
y
= Horizontal propagation coefficient, m
θ= Angle of incidence of the sound wave, °
hr
= Height of the receptor, m
Table 2 presents the classes of atmospheric stability and their relationship to the categories established by Pasquill [21].
Table 2. Atmospheric stability classes
Source: own elaboration
To calculate the horizontal σy and vertical σ
z
propagation coefficients using a mathematical model, the model proposed by McMullen through the equation 9 [21]:
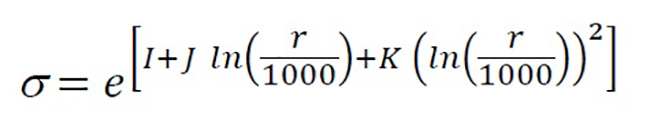 Equation 9
Equation 9
where
σ= Propagation coefficient, m
r= Distance between the source and the receptor, m
I, J, K= Empirical constants for each stability class
By comparing the dispersion of atmospheric contaminants and their relation to atmospheric stability, the horizontal and vertical dispersion coefficients from the Gaussian dispersion model were introduced into the multiple regression, which resulted in a positive correlation between the coefficients and the residual sound pressure level established in ISO 9613 Part 2. From this point forward this article will refer to the dispersion coefficients as propagation coefficients.
The propagation coefficients represent the degree of vertical and horizontal dispersion of the sound pressure levels. High standard deviation values are obtained from an atmosphere that is unstable and turbulent, whereas low values are produced by less turbulent atmospheric conditions. Table 3 shows the value of the constants for McMullen’s equation.
Table 3. Constants for the propagation coefficients according to the atmospheric stability class
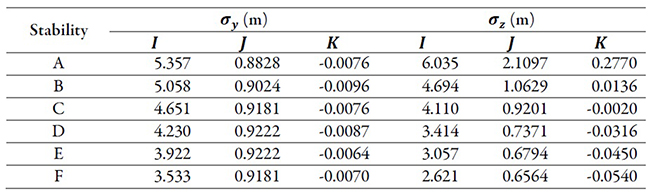
Source: Molina[21]
Results
Table 4 presents the results obtained by the noise propagation models according to the measured data. Tables 5 and 6 present differences between the measured sound pressure levels with A-weighting filters and those estimated by both the proposed propagation model and the model from ISO 9613 both in its original form and with some variations.
Table 4. Comparison of statistics between the propagation model from ISO 9613 and the proposed model
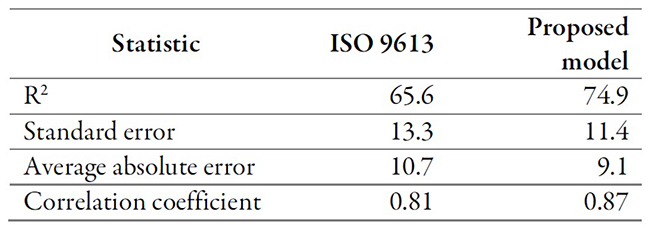
Source: own elaboration
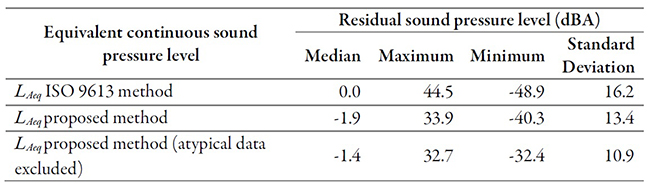
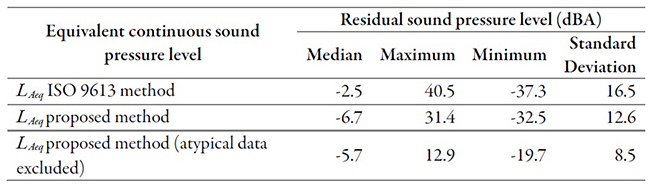
In tables 5 and 6, it can be observed that the proposed propagation model is more accurate than the method from ISO 9613 Part 2 because it exhibits values for both the standard deviation and maximum and minimum residual sound pressure levels which are lower than those obtained using the method from ISO 9613 Part 2. Using the proposed propagation model, the residual sound pressure varies between -40.3 and 33.9 dB(A), with an average of -1.9 dB(A). The residual for the wide band (20 to 20,000 Hz) equivalent continuous sound pressure level varies between -32.5 and 31.4 dB(A), with an average of -6.7 dB(A).
After eliminating the 5 % of data that were considered atypical due to studentized residuals greater than 2, the proposed model exhibits much better fit and a lower absolute average error. The studentized residuals measure the divergence of the observed residual sound pressure levels from the adjusted model using all the data and the standard deviation as a criterion.
Table 5. Differences between the estimated sound pressure levels and those measured for all stabilities, frequencies, and measurement points
Source: own elaboration
Table 6. Differences between the estimated sound pressure levels and those measured in a wide band (20 to 20,000 Hz) for all types of stability and measurement points
Source: ownelaboration
Furthermore, the residual sound pressure level varies between -32.4 and 32.7 dB(A), with an average of -1.4 dB(A). The residual for the wide band (20 to 20,000 Hz) equivalent continuous sound pressure level varies between -19.7 and 12.9 dB(A), with an average of -5.7 dB(A).
Tables 7 and 8 show statistics for the differences between the measured and estimated sound pressure levels for both the proposed propagation model and for ISO 9613 in its original form and with several variations.
Table 7. Statistics for the residual equivalent continuous sound pressure level for all types of stability, frequencies, and measurement points
Source: ownelaboration
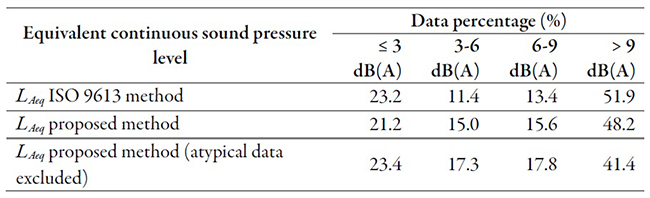
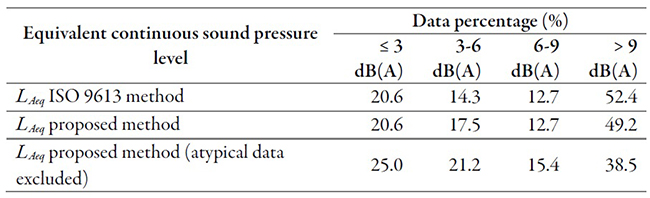
It may be observed in tables 7 and 8 that the proposed propagation model is more accurate than the method from standard ISO 9613 Part 2 because it exhibits a greater percentage of data having a residual less than or equal to 3 dB(A) or in the range between 3 and 6 dB(A).
Table 8. Statistics for the wide band (20 to 20,000 Hz) residual equivalent continuous sound pressure level
Source: ownelaboration
Through an exhaustive exercise involving both measurement and analysis, a semiempirical model is proposed for calculating sound pressure levels at various distances for noise originating from emission sources which best predicts reality or is closer to it than current standards. The proposed model can be used for predicting noise originating from a noise emission source at distances of up to 64 m, i.e., significantly improved compared with those obtained to date using the method established in standard ISO 9613 Part 2.
Moreover, the study provides a semiempirical focus that combines theoretical modeling with empirical data to solve the problem of noise propagation based on observations and measured data. Theoretical modeling seeks to understand the phenomenon of noise propagation by systematically applying the laws that govern it. However, it is impossible to perfectly capture all the real details regarding the behavior of the process using only mathematical equations. Therefore, empirical modeling uses information obtained experimentally to represent some relationships that have not yet been adequately discovered using mathematical functions, particularly when the process is extremely complex.
New focuses were used for several specific parameters in noise propagation with the aim of improving the prediction of sound pressure levels or to bring them closer to the actual situation. The reality is very complex, and therefore, it is difficult to find an analytical solution for the propagation of noise. The proposed model offers a compromise between simplicity and accuracy in the prediction of sound pressure levels associated with a noise emission source.
The residual sound pressure level obtained using the proposed propagation model varies between -32.4 and 32.7 dB(A), with a median of -1.4 dB(A). The wide band (20 to 20,000 Hz) equivalent continuous sound pressure level varies between -19.7 and 12.9 dB(A), with a median of -5.7 dB(A).
Conclusions
Unlike what was published by K. Attenborough [4], the standard method established in ISO 9613 Part 2 does not have reasonable accuracy for calculating sound attenuation during propagation in free field to predict sound pressure levels. As may be clearly observed from the data, the accuracy level of the method described in standard ISO 9613 Part 2 is not high. The maximum allowable difference between the simulated levels and the measured levels was set at 3 dB(A) [22]. For all types of stabilities, frequencies, and measurement points, 23.2 % of the data exhibit a residual that is less than or equal to 3 dB(A). For a wideband equivalent continuous sound pressure level, 20.6 % of the data exhibit a residual that is equal to or less than 3 dB(A). The correlation coefficient between the results generated by the model and the measured data is 0.81.
Other than the obvious deviations between of ISO 9613-2 calculation results and noise measurements, the other striking feature from the comparison is the lack of detail, which prevents an interpretation of the outdoor sound propagation mechanisms which come into play.
The proposed propagation model exhibits a lower standard deviation, lower error (both standard and absolute), and a greater correlation coefficient, than those of the method contained in standard ISO 9613 Part 2.
A statistically significant relationship exists between these variables at the 95 % confidence level. The standard error for the proposed prediction method is 11.4 dB(A), and the absolute average error is 9.1 dB(A). The correlation coefficient of the proposed model is 0.87.
According to the results obtained through the experimental program, the residual sound pressure level given by the proposed model is small compared to those obtained using the method established in standard ISO 9613 Part 2, particularly considering the distances involved. It may be concluded that the proposed acoustic prediction model is quite satisfactory.
As mentioned earlier, the atmospheric stability must be considered for both the measurements and the sound modeling associated with the noise emission sources. The proposed model takes the atmospheric stability into account using both stability classes and horizontal and vertical propagation coefficients.
The proposed model has more parameters than the basic components of the model established in standard ISO 9613 Part 2. Most of the model’s entry parameters are similar to those of the standard, whereas others have been made more complex, resulting in a much more precise model. The basic parameters of the model include the distance, height and sound power level of the noise source; the wind direction and speed; and the air temperature and humidity. Some of the more complex data used in the model includes the ground absorption, the atmospheric stability, and the directionality factor.
Some of these parameters are more influential than others. The main parameter is the atmospheric stability. The second is wind speed. Both the atmospheric stability and the wind speed play important roles in the propagation of sound from noise emission sources.
The physical processes present in the atmosphere cannot be studied separately because they interact with each other. Therefore, all such parameters must be studied simultaneously to avoid an underestimation or overestimation of the sound pressure levels. Indeed, attenuation due to atmospheric stability includes several parameters that have already been considered in other forms of attenuation.
This study demonstrates that the prediction model established in standard ISO 9613 Part 2 exhibits deficiencies in estimating the noise generated by a noise source. The variations in sound pressure levels are largely due to changes in weather conditions.
The proposed model is well-defined and relatively easy to use. It may be considered a “submodule” or a variation of model ISO 9613 Part 2. If the suggested adjustments are applied to the model proposed in standard ISO 9613 Part 2, then the estimated sound pressure levels exhibit a much better fit with measured levels.
It is necessary to continue advancing the in the development of models for predicting the propagation of noise from fixed noise sources in which meteorological and acoustic measurements can be simultaneously covered in an accurate and verifiable manner in order to allow the analytical solution of this problem. In addition, it is necessary to verify the performance of the noise prediction model proposed in other fixed sources of noise emissions in order to have sufficient experimental data.
References
[1] P. Economou and P. Charalampous, “A comparison of ISO 9613-2 and advanced calculation methods using olive tree lab-terrain, an outdoor sound propagation software application: Predictions versus experimental results,” Proc. Inst. Acoustics, vol. 34, no. 1, 2012.Available: http://bit.ly/2SlF1s6
[2] M. Wondollek, “Sound from wind turbines in forest areas,” Uppsala Univ., Uppsala, Sweden, Tech. Rep., 2009.
[3] M. Bérengier et al.,“Outdoor sound propagation: A short review on analytical and numerical approaches,”Acta Acust. United Ac., vol. 89, no. 6,pp. 980–991.[Online]. Available: https://www.ingentaconnect.com/content/dav/aaua/2003/00000089/00000006/art00009?trendmd-shared=0
[4] K. Attenborough, “Developments in modelling and measuring ground impedance,” in 17th Int. Congr. Acoustics, 2002, pp. 236–237.
[5] ISO 9613-2:1996. Acoustics: Attenuation of sound during propagation outdoors. Part 2: General method of calculation,1996.
[6] National Physical Laboratory, Guide to Predictive Modelling for Environmental Noise Assessment. London:National Physical Laboratory, 2007, pp. 1–30.
[7] G. van den Berg, “The sound of high winds: The effect of atmospheric stability on wind turbine sound and microphone noise,” Ph.D. dissertation, Univ. Groningen, Groningen, Netherlands, 2006.
[8] J. Cummings, “The variability factor in wind turbine noise,” in 5th Int. Conf. Wind Turbine Noise, Denver, 2013, pp. 1–17.
[9] ISO 1996-1:2003. Acoustics: Description, measurement and assessment of environmental noise. Part 1: Basic quantities and assessment procedures, 2003.
[10] ISO 3744:2010. Acoustics: Determination of sound power levels and sound energy levels of noise sources using sound pressure. Engineering methods for an essentially free field over a reflecting plane, 2010.
[11] L. Conceição, “Wind turbine noise prediction,” M.S. thesis, Eng. Aeroesp., Ins. Sup. Téc., Univ. Téc. Lisboa, Lisboa, Portugal, 2008.
[12] P. Moriarty and P. Migliore, “Semi-empirical aeroacoustic noise prediction code for wind turbines,” Nat. Ren. Energy Lab.,Dec.2003.[Online].Available: http://citeseerx.ist.psu.edu/viewdoc/download?
[13] W. Zhu, “Modelling of noise from wind turbines,” M.S. thesis, Wind Energy, Tech. Univ. Denmark, Lyngby, Denmark,2004.
[14] S. Hoogzaad, “Measuring and calculating turbine noise immission in the Netherlands,” in IEAWind expert meeting sound propag.mod., Stockholm, 2009, pp. 7–16. Available: http://bit.ly/2LsNRUj
[15] S. Oerlemans et al., “Location and quantification of noise sources on a wind turbine,” J. Sound Vibration, vol. 299, no. 4-5, pp. 869–883, Feb. 2007.doi: 10.1016/j.jsv.2006.07.032
[16] K. Attenborough, “A review of ground impedance models for propagation modelling,” in Forum Acusticum Sevilla, 2002, pp. 1–6.
[17] J. Prospathopoulos and S. Voutsinas, “Application of a ray theory model to the prediction of noise emission from isolated wind turbines and wind parks,” Wind Energy, vol. 10, no. 2,pp. 103–119, Mar. 2007.doi: 10.1002/we.211
[18] P. Fuglsang and H. Aagaard, “Implementation and verification of an aeroacoustic noise prediction model for wind turbines,” Risø Nat. Lab. Mar.1996. [Online]. Available: http://orbit.dtu.dk/fedora/objects/orbit:90419/datastreams/file_e8a71a1b-af6e-4b39-a587-f0c70097d5ac/content
[19] H. Kruse, “In-situ measurement of ground impedances,” Ph.D. dissertation, Fakultät Mathematik Naturwissenschaften Carl Ossietzky, Univ.Oldenburg, Oldenburg, Germany, 2008.
[20] J. S. Lamancusa, Noise Control. Pennsylvania: Pennsylvania State University, 2000.
[21] F. Molina, O. Rengifo, and F. Vélez, “Modelo de dispersión gaussiano de contaminantes atmosféricos,” Rev. AINSA, vol. 13, no. 1, pp 33–47, En. 1993.
[22] C. A. Echeverri et al., “Simulación de ruido de tránsito automotor como herramienta para el rediseño de rutas de transporte público colectivo en el municipio de Medellín,” Rev. Ing. Univ. de Medellín, vol. 10, no. 18, pp. 19–29, Jun. 2011. Available: http://bit.ly/2Yc09Xf
Notes
* Research article
This article is derived from “Evaluation of the method specified in standard ISO 9613-2 for the prediction of sound pressure levels generated by fixed sources” investigation project.
How to cite this article:
C. Echeverri Londoño, andJ. Ortiz Pabón,“Model for the prediction of noise generated by fixed sources,” Ing. Univ.,vol. 23, no. 2, 2019. https://doi.org/10.11144/Javeriana.iyu23-2.mpng
Author notes
a Autor de correspondencia. Correo electrónico cecheverri@udem.edu.co