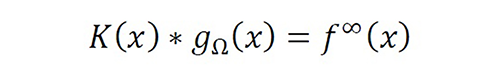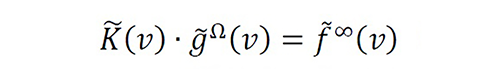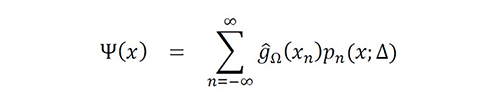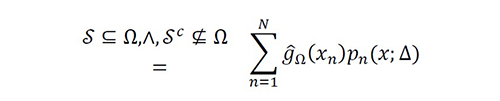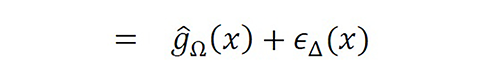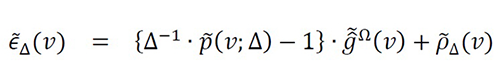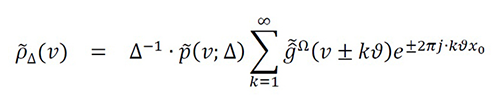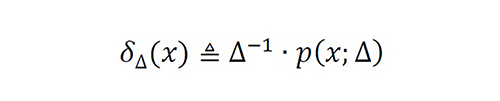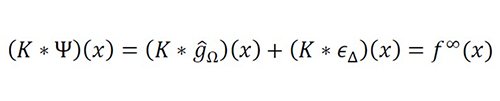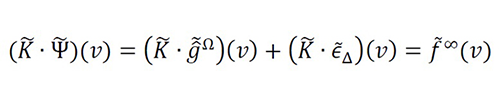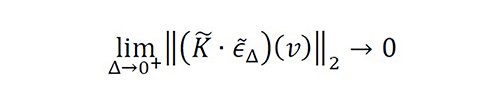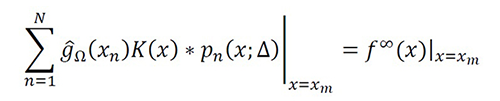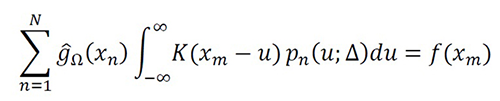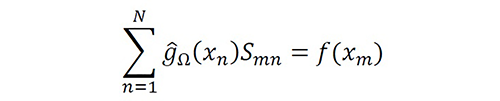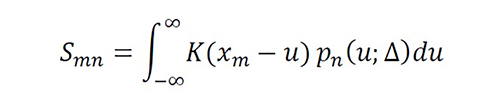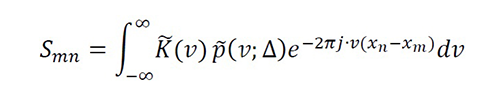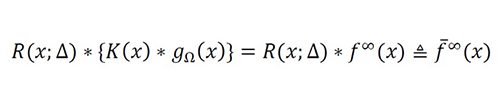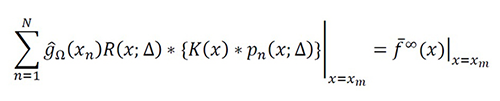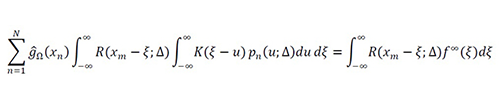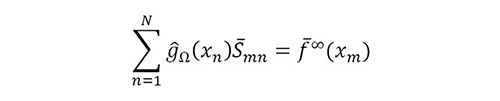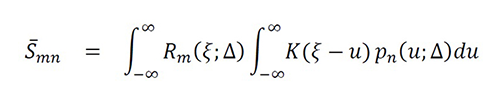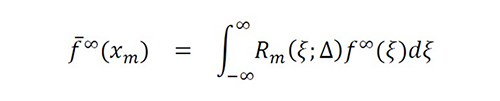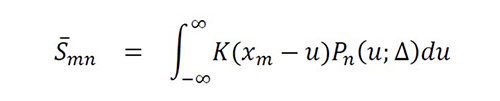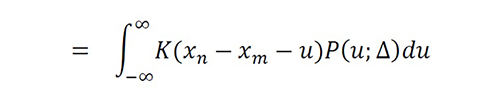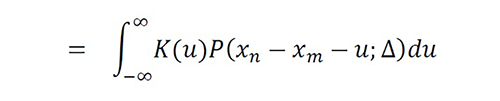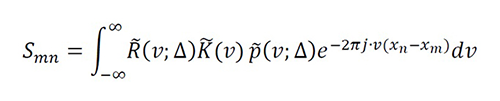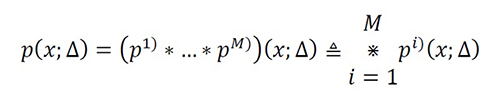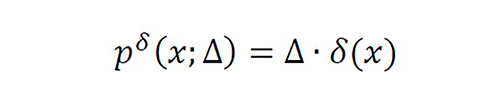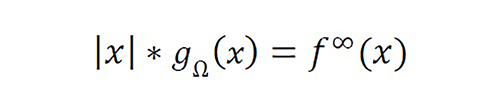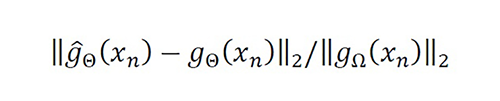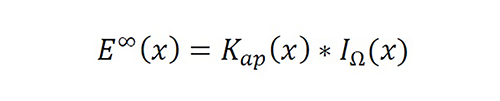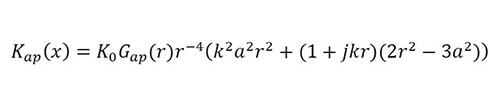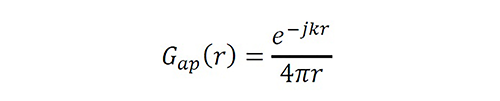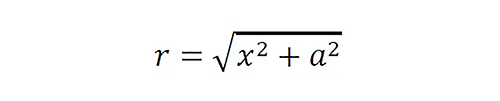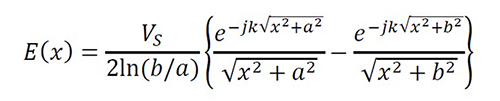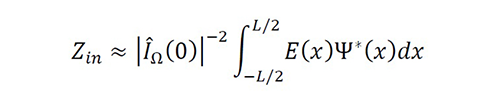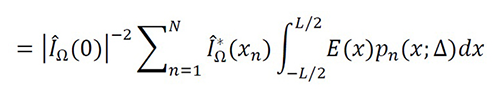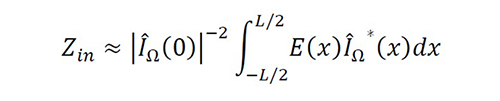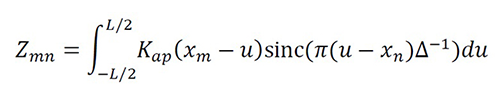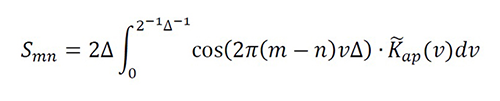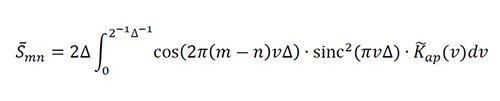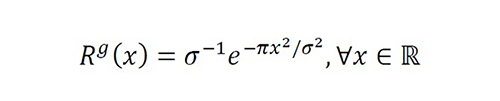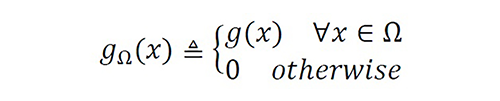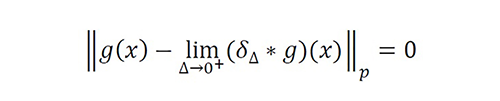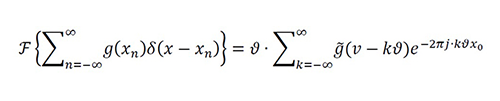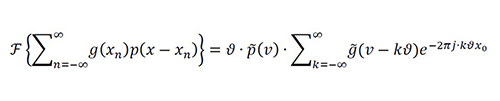Main Nomenclature
g(x) Unknown function over the interval .
f(x) Known function over the interval .
K(x,u) Kernel of the integral equation.
gΩ (x) Truncated function of over the interval x∈R .
f∞ (x) Extended function of over the interval x∈R.
gΩ (xn) Instantaneous value of at sample xn∈R.
g ̂ Ω (xn) Instantaneous approximation of gΩ (xn ).
Ψ(x) Nonideal sampling function over the interval x∈R.
ϑ Sampling rate.
pn (x;Δ) Generalized interpolation function over the interval x∈R .
h ̃(v) Fourier transform of h(x).
g ̃Ω (v)Fourier transform of gΩ (x).
BW2
h Essential bandwidth of ∈L2 .
L1∧2 Means L1∩L2 .
Mathematical definitions and other notations can be found in appendicesA.1 and A.2.
Introduction
Integral equations (IEs) allow the modeling of a large number of complex problems in several areas of engineering and physics such as heat and mass transfer, oscillation theory and electromagnetic fields. An IE is an equation in which an unknown function related to an integral needs to be found under a known excitation . Some examples include one-dimensional IEs with forms ∃g(∙):∫a
b K(x,u)g(u)du=f(x) and ∃g(∙):∫a
xK(x,u)g(u)du=f(x), which are respectively known as the Fredholm and Volterra equations of the first kind, in which is usually known as the kernel.
Several techniques have been developed over the years to solve this kind of problem using exact, asymptotic and numerical approaches. A comprehensive summary of these techniques for different problems can be found in [1]–[3]. In particular, a well-known numerical technique to solve electromagnetic problems using IEs is called the method of moments (MoM) [4], [5]. This approach allows the development of a general framework including different types of modern techniques, known as the method of weighted residuals (MWR). For example, the finite element method (FEM) and the finite difference method (FDM) can be represented using the MWR [6], [7]. In recent times, the MoM has been used to solve multidimensional open boundary problems in electrodynamics, and it is included in many CAD platforms such as HFSS, IE3D, FEKO, and NEC.
In [8], we proposed an original approach to solve integral equations, based on the nonideal instantaneous sampling theory, which involved developing a novel framework for solving linear operators using Fourier analysis. The new approach was based on the fact that a Fredholm equation of the first kind with a difference kernel K(x,u)=K(x-u) can be expressed as an extended convolutional problem with form K(x)*gΩ (x)=f∞ (x) , where where is a truncated function of , is an extended function of , , and is the standard convolution operator. As a result, although the problem must be solved via matrix techniques using the original domain, the convolution properties and Fourier analysis can be used to design an efficient solution. This new property, known as the convolutional equivalence, allows the establishment of design rules that cannot be determined when using the MoM. These results are detailed in this paper through a new framework termed as the method of sampling for one dimension (MoS!-1D).
Most previous works aimed at solving Fredholm equations in the context of electrodynamics were focused mainly on the MoM. The different approaches established benchmarks for computational techniques (e.g., the comparison between MoM, FEM and FD-TD) and experimental techniques (e.g., the wire antenna) and identified particular computational issues (e.g., extremely ill-conditioned matrices), and they have been the cornerstone for generalizations in two and three dimensions. For example, [4] and [9] solved the problem of wire antennas with arbitrary shapes; [10] and [11] used telegraphist’s equations to evaluate transmission lines by using the Green function; [12] proposed the use of semiorthogonal compactly supported spline wavelets to evaluate an infinitely long metallic cylinder illuminated by a TM plane wave; [13] found the unknown current of a linear dipole with MFIE using high-order basis functions; and [14] and [15] solved the scattering for an infinite curved smooth strip considering the TM and TE cases by using the Nystrom method. However, few discussions exist regarding the relationship between the system theory based on the convolution operator and the Fredholm equation in the context of electrodynamics. Notably, [16] defined an effective bandwidth of a scattered field using the bandlimited behavior of the far field. Subsequently, [17] and [18] used this property to define basis functions with better convergence based on the entire domain and quasi-localized bandlimited interpolation functions. Furthermore, [19] used this behavior to simplify the Green function by removing the unexpected spectral components. This approach was supported by the similarity of the problem with a convolutional formulation, which was not very well defined.
The main contributions of this paper are new design paradigms and strategies for solving a Fredholm equation of the first kind, which covers the MoM methodology. For instance, we found that the functions used to determine a linear equation system can be designed as generalized interpolation functions without the assumption of continuity or smoothness, the weighting functions are sampled linear filters with particular specifications, and the new matrix coefficients Smn may contain information concerning the supradomain (x ∈ Ωc). In the same manner, we proved that the generalized interpolation functions can be different from the functions used to approximate the unknown continuous function, and it is possible to reduce the computational cost based on the properties of linear and invariant systems.
The remaining sections of the article are organized as follows: in method of sampling section describes the justification and development of the novel approach using the nonideal instantaneous sampling theory. In analysis and evaluation section, several aspects of the matrix approach are discussed, and two examples are numerically evaluated. In conclusions, we present the conclusions of this research. Finally, appendices A and B detail several definitions, theorems and properties needed to make this paper self-contained.
Method of Sampling
Convolutional Equivalence
Assume a convolutional integral equation (CIE) with the form ∃g(∙):∫ab K(x,u)g(u)du=f(x) with a<b ∀x∈Ω≜[a,b]⊂R, and K(x,u)=K(x-u). . Let K∈L2 and gΩ ∈ L1∧2 with the essential bandwidths being and (see definition 8).
Consider the extended equivalent problem ∃gΩ (∙):∫-∞
∞ K(x,u)g(u)du=f∞ (x)=fΩ
∞ (x)+fΩc
∞ (x) , with fΩ
∞ (x)=fΩ (x) and Ωc=R-Ω [8]. From this formulation, the extended function f∞ (x) has two components: The first (fΩ
∞) is the known function because fΩ (x)={f(x),∀x∈Ω and zero elsewhere ; the second (fΩc
∞) is the extended function f∞ (x) evaluated in the supradomain (x∈Ωc),which is a degree of freedom with mathematical sense allowing the hypothesis gΩ K→ f∞.For a major discussion concerning this equivalence,see [8].
The analysis of this new problem can be performed in the original domain (x-domain) or the Fourier domain (v-domain) by using
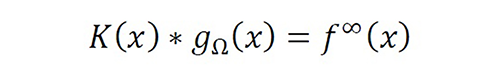 Equation 1
Equation 1
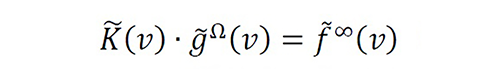 Equation 2
Equation 2
where f∞∈L2 with BW2
f∞ . The critical bandwidth of this new problem is denoted by BW=min{BW2
f∞,BW2
fΩ∞} .
The solution of this problem must be in the domain because the degree of freedom f(Ω
c)∞ (x) is unknown, and even though this function makes mathematical sense, it is not related to the physics of the original problem.
Asymptotic Reduction
Let xn ∈ {...,x-1,x0,x1,…} be sampling points such that S≜{x1,…,x_N}⊆Ω and S^c≜{…,x-1,x0,xN+1,xN+2,…}⊈Ω . Let Ψ(x) be a nonideal sampling function defined by
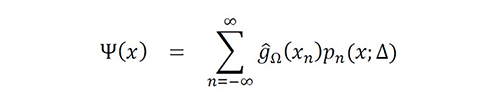 Equation 3
Equation 3
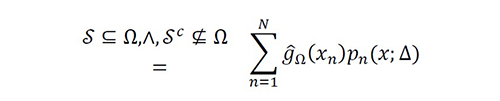 Equation 4
Equation 4
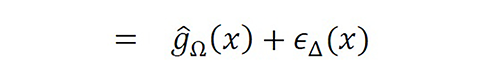 Equation 5
Equation 5
where g ̂Ω (xn ) is an instantaneous approximation of gΩ (xn ), and pn (x;Δ) is a generalized interpolation function [8].
In contrast with other computational methods developed so far, the nonideal sampling function Ψ(x) is not necessarily a satisfactory representation of gΩ(x) in the conventional sense (e.g., variational sense). This fact means that Ψ(x):∆ >0 does not necessarily minimize a continuous error, such as min∀x∈Ωmax|Ψ(x)-gΩ (x)| , min∫Ω|Ψ(x)-gΩ (x)|dx or min∫Ω(Ψ(x)-gΩ (x))2 dx , as can be inferred from figure 1. We use functions such that g ̂Ω(x) and ϵΔ (x) are asymptotically (Δ→0+) separable through the v-domain. As a result, Ψ(x) is not necessarily conformed by a combination of orthogonal or smooth functions with domain Ω (see figure 1).
If we use uniform generalized interpolation functions p_n (x;Δ)=p(x-xn;Δ)=p(x;Δ)*δ(x-xn) with domain Ωpn ⊆R and uniform samples xn=xn-1+Δ=x0+nΔ, the spectral error is (see theorem 11)
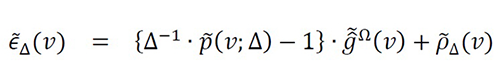 Equation 6
Equation 6
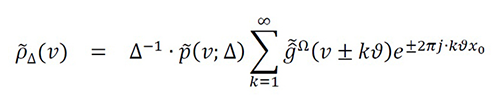 Equation 7
Equation 7
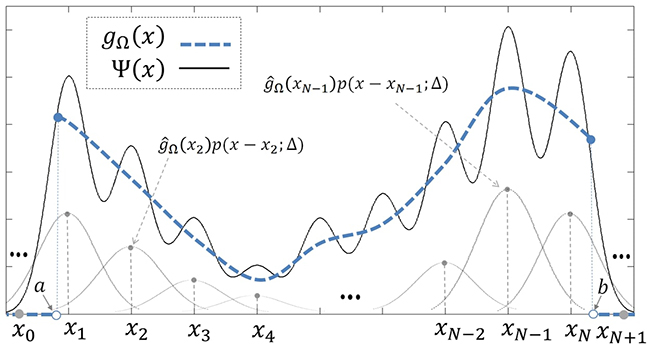 Figure 1. Conceptual example of a generalized interpolation function proposed in this paper
Figure 1. Conceptual example of a generalized interpolation function proposed in this paper
Source: Páez [8]
Therefore, the spectral error function ϵ ̃Δ (v) has three spectral components: The first component is the distortion of {∆-1∙p ̃(v;Δ)-1} in |v|≤BW. The second component is the interference of in ρ ̃∆ (v) in |v|>BW. From (7), this interference may be centered at the harmonics ±kϑ , and it may be located in the intervals |v±kϑ|≤BW . The third component is the aliasing of ρ ̃∆ (v) in |v|≤BW . Consequently, if
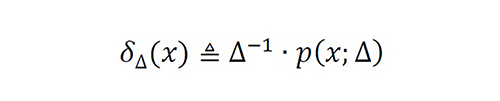 Equation 8
Equation 8
is a nascent Delta-Dirac function, then the distortion and aliasing are asymptotically removed via ϵ ̃Δ (v) for gΩ ∈ L1∧2 using the Nyquist criterion ϑ≜Δ-1>2BW . If the Nyquist criterion is not satisfied, the aliasing cannot be controlled, and therefore, it is not possible for convergence to occur in the problem.
v-domain to be defined as follows:
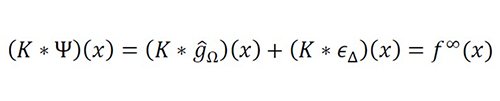 Equation 9
Equation 9
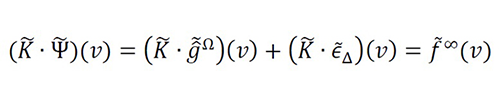 Equation 10
Equation 10
The novel approach is based on the solution of this new problem assuming the asymptotic reduction of the spectral error, summarized by
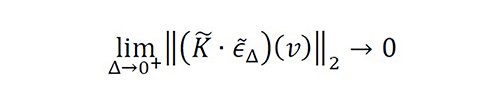 Equation 11
Equation 11
As a result, g ̂Ω (x)→gΩ (x) and g ̂Ω (xn )→gΩ (xn ) almost everywhere. Therefore, the relations among the interpolation function p(x;Δ) , kernel K(x) and sampling rate (ϑ≜Δ-1) to achieve this particular behavior are not arbitrary.
Remark 1.Because we do not know g ̂Ω (x) a priori, our methodology only obtains the instantaneous values g ̂Ω (xn ) [8]. Consequently, a smooth interpolation algorithm, denoted by J{∙} , must be used to find the unknown continuous approximation given by g ̂Ω (x)=I{g ̂Ω (xn )}, under the hypothesis of compliance with the Nyquist criterion.
In contrast with other methodologies, the proposed approach allows the determination of several design strategies and interpretations to solve linear operators using Fourier analysis. For clarity and space reasons, we discuss only two of these strategies below.
Bandwidth Matching Procedure (BM-P)
We propose a general methodology to solve a CIE assuming that the combination of the interpolation functions and the kernel allows the undervaluing of the influence of the spectral error in the problem, for example, by assuming BW2
gΩ ≫BW2
K or ‖(K ̃∙g ̃Ω )(v)‖2≫‖(K ̃∙ϵ ̃Δ )(v)‖2 .We name this technique the bandwidth matching procedure (BM-P).
x=x_m∈S i Without loss of generality, if we take samples at i in (9),
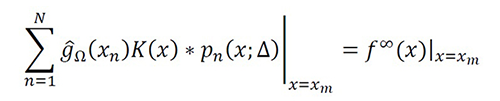 Equation 12
Equation 12
Rewriting (12) in integral form, we obtain
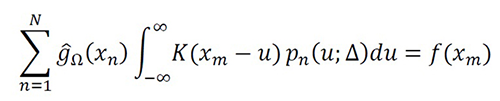 Equation 13
Equation 13
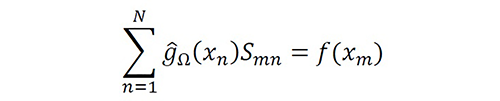 Equation 14
Equation 14
The linear equation system using BM-P is SΨ=f with Ψ=[g ̂Ω (xn )], f=[f(xm)] and S=[Smn ], where g ̂Ω (xn ) is an instantaneous approximation of gΩ (xn ), f(xm) is the instantaneous value printed by the output, and Smn is the instantaneous equivalent system between the samples, defined as
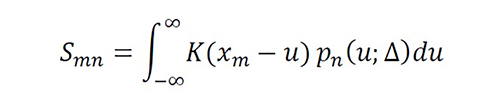 Equation 15
Equation 15
Corollary 2.
If we design pn (∙;Δ) as the basis functions and Ωpn ⊆Ω , the BM-P obtains the same equations as those used by the MoM when using the point matching procedure (PM-P).
If the Fourier transform of the functions are well-defined and holds F{K(x)*p(x;Δ)}=K ̃(v)p ̃(v;Δ) with K ̃∙p ̃∈L1 , another way to evaluate the system coefficients [8] is by using
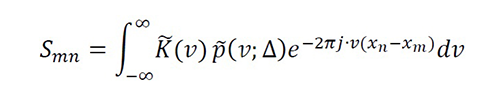 Equation 16
Equation 16
Regularization Technique by Convolution (RT)
We propose another general methodology to solve a CIE assuming some spectral anomaly, for instance BW2
gΩ≪B_2
K or ‖(K ̃∙g ̃Ω )(v)‖2≪‖(K ̃∙ϵ ̃Δ )(v)‖2 . In this case, we propose the regulation of (1) using R(x;Δ) with the convolution operator (literally, filtering the problem) as
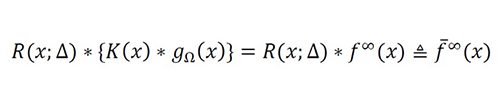 Equation 17
Equation 17
such that the new system can be modeled as a well-defined low-pass problem with a new critical bandwidth (BW) ̅<BW. We name this technique as the regularization technique by convolution (RT).
Therefore, to have asymptotic convergence toward the original problem, we design the filter R(x;Δ) as a nascent Delta-Dirac function with nulls specifically located to reduce the spectral anomalies in the problem. In particular, we design these nulls to remove asymptotically the last component of the spectral error, that is, the harmonic interference.
Without loss of generality, if we take samples x = xm∈ S at in the new equivalent instantaneous problem,
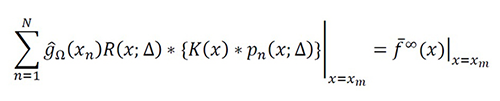 Equation 18
Equation 18
Rewriting (18) in integral form, we obtain
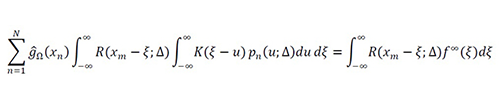 Equation 19
Equation 19
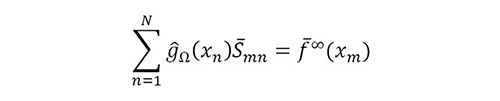 Equation 20
Equation 20
where the function Rm (ξ;Δ) = R(xm-ξ;Δ) is literally the sampled impulse response of a standard linear filter.
The linear equation system using RT is S ̅Ψ = f ̅ with Ψ = [g ̂Ω (xn )], f ̅=[f ̅∞ (xm)], and S ̅=[S ̅mn ], where g ̂Ω(xn ), is an instantaneous approximation of gΩ (xn) considering the filter R(x;Δ), f ̅∞ (xm) , is the instantaneous value printed by the regularized output, and S ̅mn is the new instantaneous equivalent system between the samples given by
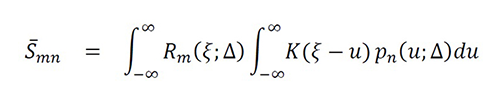 Equation 21
Equation 21
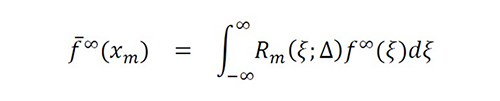 Equation 22
Equation 22
If we design R_m (ξ;Δ) with subdomains (ΩRm⊂Ω) or entire domains (ΩRm =Ω) to avoid unknown information of f∞ (x), the resulting respective techniques are called the subdomain regularization technique (S-RT) and the entire domain regularization technique (E-RT).
Corollary 3. If we design pn (∙;Δ) as the basis functions, Rm (∙;Δ) as the weighting functions related to an interior product, and Ωpn,ΩRm ⊆Ω, the RT obtains the same equations as those used when applying the general approach of the MoM (and in general, those employed when using the MWR).
If it is possible to use the associativity property R*{K*Ψ}={R*K}*Ψ=K*{R*Ψ} (e.g., see Fubini’s theorem and Hölder’s inequality), the formulation can be simplified and computational cost can be reduced by using ∑n
N=1gΩ (x
n) K(x)*Pn (x;∆)= f ̅∞ (x) because Pn
(x;∆)≜(R*pn
)(x;∆) and ΩPn ≜ΩR*Ωpn may have closed forms. The new function P_n (x;∆) is known as an ultrafunction, and the simplified formulation as termed as the ultra-RT. In this case, the system coefficients [8] can be obtained using
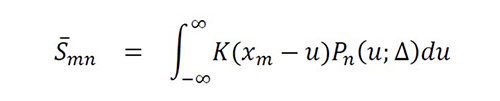 Equation 23
Equation 23
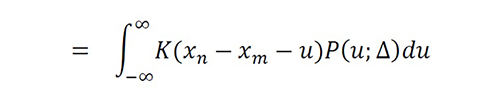 Equation 24
Equation 24
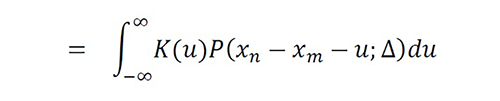 Equation 25
Equation 25
Finally, if the Fourier transforms of the functions are well defined and F{R(x;Δ)*K(x)*p(x;Δ)}=R ̃(v;Δ) K ̃(v)p ̃(v;Δ) holds with R ̃∙K ̃∙p ̃∈L1,
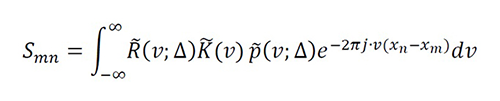 Equation 26
Equation 26
From (10) and (17), if we choose R(x;Δ)=∆-1∙p(x;Δ), the harmonic interference can be reduced by using a quadratic factor. In the same way, if the related functions are designed as in the MoM, this technique can be considered an alternative explanation of the Galerkin method, and it can easily explain under what conditions the solution can be successfully applied [8].
Design Considerations
The asymptotic reduction is obtained and justified using the sample theory in the following manner. The distortion is asymptotically removed by choosing the interpolation function as a nascent Delta-Dirac function because lim┬(Δ→0+)δ ̃Δ (v)→1:∀|v|≤BW. The interference is reduced by designing the interpolation functions (and the filter) with spectral nulls at the harmonic interference, given by |δ ̃Δ (v)|≤δI≪1,∀|v±kϑ|≤BW, k ∈ N. This interference is asymptotically removed by increasing the sampling rate because the kernel has a finite bandwidth. The spectral nulls should be designed to exactly match with this interference to reduce the possibility of occurrence of ambiguities caused by the nonexistence of f(Ωc
∞
(x). Finally, the aliasing is asymptotically removed by increasing the sampling rate because ∀g ̂Ω ∈ L1∧2 has the property lim┬(v→∞)g ̂ ̃Ω (v)→0. As a result, lim┬(Δ→0)g ̂ ̃^Ω (v±kϑ)〗→0:∀|v|≤BW,k∈N and lim┬(Δ→0+)ρ ̃∆ (v)〗→0:∀|v|≤BW. For details and examples of these considerations, see [8].
Analysis and Evaluation
Novel Approach to Solve Convolutional Integral Equations
Because the approach of the MoS! has a different way to obtain convergence, to the best of the author’s knowledge, our proposal is an innovative framework for solving Fredholm equations of the first kind. The MWR solves ∃g(∙):L{g}=f by using g ̂=∑n
N=1αn bn, such that the residual error r=L{ĝ}-f is reduced by means of the interior product ⟨r,Rm ⟩=0 [4]. The novel approach includes the same interpretation because the same equations are determined when Ωpn,ΩRm ⊆Ω, albeit with new paradigms and degrees of freedom. We highlight the following aspects of our methodology.
Before taking the samples xm in (12) and (18), the functions p(x;Δ) and R(x;Δ) can be designed to reduce the error in both domains because ‖ϵ ̃Δ (v)‖2=‖ϵΔ (x)‖2. A more comprehensive approach to design R(x;Δ) (and the problem) using the communication theory may be considered because that function is not necessarily related to a reduction in the residual error in the sense of a geometric projection. For instance, the filter R(∙;Δ) may be designed as a standard receptor system with several roles related to reducing the noise caused by the rounding errors (e. g., pre-emphasis and de-emphasis techniques and matched filter) and transforming a dense matrix in a sparse matrix (e. g., intersymbol interference techniques).
After taking the samples xm in (12) and (18), the obtained matrices SΨ=f and S ̅Ψ=f ̅ are the formulations of a standard discrete-time system (formally a discrete x-domain system), in which it is now evident that all the information between the samples xm and xm+1 is lost because, in general, f∞ (x) and f ̅∞ (x) are not bandlimited functions. As a result, Ψ(x) is not necessarily a good continuous approximation of the unknown function gΩ (x).
Remark 4. The only methodological difference between BM-P and RT is that the original problem is regularized by a filter to obtain a slower problem. As a consequence, the MoM (and, in general, the MWR) is an instantaneous technique, or “point matching procedure”, independent of the weighting functions.
Discussion Concerning Interpolation Functions
A standard interpolation function is defined as a basis function in the context of being used by standard numerical methods such as the MoM. For instance, the well-known rectangular and triangular basis functions are pn
Π (x;Δ)=ΠΔ (x-xn) and pn
Λ (x;Δ)=ΛΔ (x-xn). Our approach allows the analysis of these functions because their Fourier transforms are well defined by p ̃Π (v;Δ)=ϑ-1 sinc(πv/ϑ) and p ̃Λ (v;Δ)=ϑ-1sinc2 (πv/ϑ).
Consequently, to maintain the distortion in 0.95≤|Δ-1∙p ̃(v;Δ)|≤1,∀|v|≤BW, it is required that BW≤0.175ϑ and BW≤0.124ϑ. As a result, the minimum sampling rate with that distortion for pΠ (∙;Δ) is ϑ= 0.175-1 BW≥6∙BW and that for pΛ(∙;Δ) is ϑ= 0.124-1 BW≥9∙BW.
These results prove that if the kernel has a narrow bandwidth such that it reduces the interference of the sampling process, the rectangular function should unexpectedly obtain a better accuracy than the triangular function does because the distortion is lower at the same sample rate.
In contrast, because the reduction in the first harmonic interference is given by |Δ-1∙p ̃(v;Δ)|<δI
±1,∀|v±ϑ|<BW with δI
±1.Π=0.2016 and δI
±1.Λ=0.0192, the triangular function should demonstrate superior performance in the kernels with wide bandwidths (e. g., kernels with some singularity or quasi-singularity) because the main harmonic interference of the sampling process is one decade lower at the same sample rate. From our approach, it is now evident that the rectangular function does not necessarily minimize ‖Ψ(x)-gΩ (x)‖, although the instantaneous value g ̂Ω (xn) may be more accurate.
A generalized interpolation function is defined in a different direction using the asymptotic separability in the domain between the unknown approximation and the error. As a result, Ψ(x) may not be a standard representation of gΩ (x), (see figure 1). Nevertheless, these functions require careful design to avoid the numerical instability caused by the spectral mismatch (e.g., new spectral nulls in the problem). An uncomplicated method to formulate a generalized interpolation function is
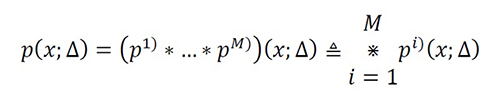 Equation 27
Equation 27
where p̃(v;Δ)=∏M
i=1p ̃i (v;Δ) and Δ-1∙p(x;Δ) represent a nascent Delta-Dirac function with nulls located strictly in the harmonic interference of the sampling process. To demonstrate this methodology, the authors propose pe (x;Δ)=(p1)*p2))(x;Δ) as an example, such that p1) (x;Δ)=ΠΔ (x)-c/2 ΠΔ (x+Δ/2)-c/2 ΠΔ (x-Δ/2) and p2) (x;Δ)= t1∙ΠΔ (x), as shown in figure 2a.
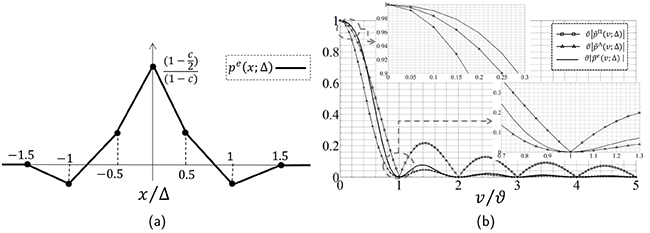 Figure 2. Generalized interpolation function pe(x;Δ)
Figure 2. Generalized interpolation function pe(x;Δ)
(a) Model in the domain
(b) Model in the domain
Source: Páez [8]
The formulation of this unusual combination in the v-domain is p ̃e (v;Δ)=(p ̃1)∙p ̃2) )(v;Δ)=t1 ϑ-2 sinc2 (πv/ϑ){1-c∙cos〖(πv/ϑ)〗}; therefore, to achieve the nascent Delta-Dirac behavior, the constant t1=ϑ/(1-c). Figure 2b shows that if c=1/3, p ̃e (v;Δ) increases the linearity regarding p ̃Π (v;Δ), and the spectral nulls have a similar attenuation to p ̃Λ (v;Δ). As a result, using low-pass kernels, this interpolation function ought to exhibit better performance and low computational cost. The function defined in this example is similar to those defined by the wavelet theory, although it does not necessarily imply a good continuous representation of the original function or a multiresolution signal decomposition.
Remark 5. Because the rectangular and triangular functions are nascent Delta-Dirac functions with nulls at ±kϑ, that basis functions are generalized interpolation functions, as well. The main difference between MoM and MoS! in these cases it is that the instantaneous values g ̂Ω (xn ) may allow a better continuous approximation than Ψ(x) does.
Finally, if |K ̃(v)| is strongly decreasing toward zero at high frequencies, it is possible to define
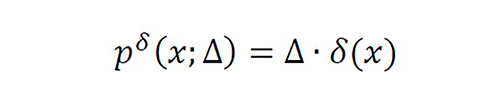 Equation 28
Equation 28
because (46) is proved from (45). As a result, some low-pass kernels may have a convergent closed-form matrix using high sampling rates , which allows the study of an analytic or asymptotic inverse for the problem, using the digital signal processing framework.
Example 1: ANarrow Band Kernel
The problem with is the CIE of the differential equation , where is not an arbitrary function. This function must have some properties [1] such as appropriate boundaries , and it must be a bounded twice-differentiable function with a bounded first derivative. As a theoretical and numerical benchmark, we propose and
Using our approach, the extended convolutional model is
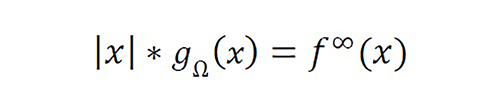 Equation 29
Equation 29
where Ω=[0,1], K(x)=|x|, fΩ
∞ (x)=fΩ (x), and f(Ωc)
∞ (x) is a degree of freedom with mathematical sense. Because d/dx |x|=sgn(x),∀x≠0, K ̃(v)=-1/(2π2 v2 ),∀v≠0.
In this problem, it not possible to use the v-domain to calculate the matrix coefficients because K ̃(v) has a distribution not calculated at v=0. However, the Fourier domain interpretation is reasonably valid because the Fourier transform is well defined using the distribution theory, and the convolution operator is well established in this problem for a finite interval Ω. As a result, by using the spectral interpretation for ∀v≠0, it is valid to assume that this problem is a narrowband kernel for BW≥π-1 2-1/2.
The matrix formulation simplifying Ω=(0,1) for pΠ (x;Δ) is (I+4B)Ψ=4ϑ2 f, where B=[B_mn ]=[|m-n|] and I is the identity matrix; for pΛ (x;Δ) is (I+3B)Ψ=3ϑ2 f, and for pΠ (x;Δ) and RΠ (x;Δ)=Δ-1 ΠΔ (x) is (I+3B)Ψ=3ϑ2
f ̅, where f ̅m=π-1-2π-2 sin(πxm)sinc(1/2 π∆). From the MoM approach, the first two formulations pertain to the PM-P, and the last one pertains to the Galerkin method.
The matrix formulation using the MoS!-1D with pe (x;Δ) is (T+B)Ψ=ϑ2 f, where T is an uniform tridiagonal matrix with coefficients T1,1=12-1 (4-7c)(1-c)-1 and T1,2=24-1 (24-25c) (1-c)-1-1. We emphasize that this solution is different from the MoM approach because the integrals have different domains.
Figure 3 compares the different estimations through the relative residual error
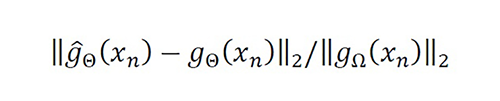 Equation 30
Equation 30
for Θ≜[10,1-10Δ]; in this case, several new paradigms are evident. Because a low-pass kernel is more relevant for the distortion rather than the interference, the function p^Π (∙) finds a better outcome than pΛ (∙) does, and the new proposal pe (∙) has a significantly better performance for Θ, with a different slope (logarithm) of convergence. For instance, the number of unknown variables for an instantaneous relative residual error of 10-7 is N≈50 for pe (∙) using the MoS! and N≈2000 for the classical low order functions using the MoM.
Nevertheless, we note that pΛ (∙) still exhibits better elimination of the first harmonic interference in figure 2b. This little energy is accumulated at the boundaries at xn∈(0,9Δ]∪[1-9Δ,1). As a result, this location is the only one at which pΛ (∙) exhibits better performance in this problem.
Considering special interpolation functions, we found an inverse with linear complexity using p^δ (x;Δ). The solution in this case is Ψ=∆-2 B-1 f, where B-1 is detailed in appendix B. This matrix solution is similar to the matrix used by FDM for g(x)=1/2 d2/dx2 f(x). This solution exhibits the same performance as pΛ (∙), thereby proving conclusively that the interference is not dominant in this problem. The theoretical matrix B-1 allows the solution of the general case (I+βB)Ψ=βϑ2 f by applying the Neuman series by means of Ψ≈{β-1 B-1+⋯+(-1)k+1 β-k B-k}βϑ2 f for N≥3 and ρ+ (β^(-1) B^(-1) )<2β-1<1. As shown in figure 3, this algorithm converges with k=3 in the same way as Gaussian elimination for the rectangular (β=4) and triangular (β=3) cases.
This problem exhibits ill conditioning at high sampling rates (or breakdown segmentation) because this kernel has extremely low spectral information at extremely high frequencies. From figure 3, the breakdown for the classical basis functions can be noted at and that for pe (∙) can be noted at N≳400
In summary, several of the new paradigms were distinguished in this example. First, we demonstrated that Ψ(x) is not necessarily the best way to represent the unknown function because the rectangular function exhibits a better instantaneous performance than the triangular function does. Second, we demonstrated that the Galerkin method does not increase the accuracy because this problem is not anomalous at high frequencies. Consistent with the ultraformulation, the same system matrix is found using the triangular function with PM-P and the rectangular function with the Galerkin method. As a consequence, any difference between both results can only be interpreted by filtering of the source. Third, considering the example of pe (x;Δ), the use of generalized interpolation functions with supradomain information can significantly increase the accuracy. Finally, we demonstrated that the formulation based on pδ (x;Δ) can be used to design asymptotic techniques to solve this narrowband problem.
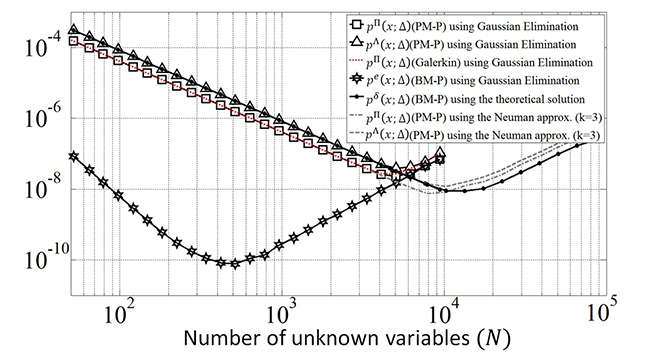 Figure 3. Instantaneous relative residual error using different interpolation functions in example 1
Figure 3. Instantaneous relative residual error using different interpolation functions in example 1
Source: Páez [8]
Example 2: AWideband Kernel
To discuss the novel approach using a standard electromagnetic benchmark, the authors solved the unknown current of a linear dipole with radio 0<a≤10-2 λ and length L≫a using the reduced or approximate Pocklington equation under a particular printed source E(x). Without loss of generality, we use the Richmond simplification [20] to use a standard CIE. The extended convolutional problem is
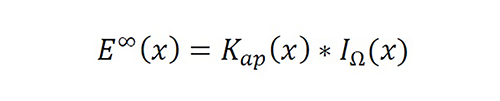 Equation 31
Equation 31
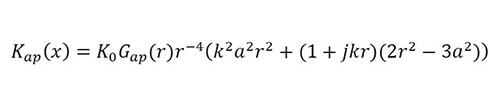 Equation 32
Equation 32
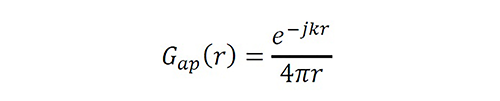 Equation 33
Equation 33
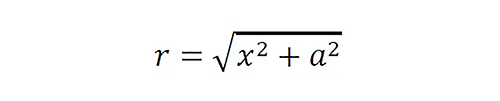 Equation 34
Equation 34
where x∈R, Ω=(-L/2,L/2), K0=j∙(2πfϵ)-1, j=√(-1), c=λf, k=2π/λ, f [Hz] is the frequency, c [m/s] is the speed and λ [m] is the wavelength in a medium with permittivity ϵ [F/m], EΩ
∞ (x)=EΩ (x) is the printed source in Ω, and EΩc
∞ (x) is a degree of freedom with mathematical sense.
This quasi-singular kernel can be understood from the Fourier transform K ̃ap (v)=F{Kap (x)} approximated through the DFT with samples xn=a/150 n. For instance, figure 4c details log10 |K ̃ap (vn )| using a=0.05λ and λ=1 m, in which several behaviors are evident.
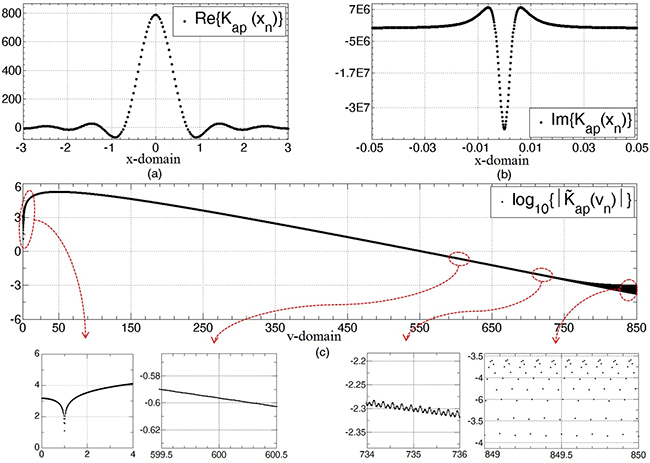 Figure 4. Reduced kernel using and
Figure 4. Reduced kernel using and
(a) Real part of Kap (x)
(b) Imaginary part of Kap (x)
(c) Approximate logarithm transfer function by means of DFT
Source: Páez [8]
As expected, this kernel has a large bandwidth caused by its quasi-singularity. We find a local minimum at v=±1 (and, in general, at v=±λ-1) related to the main spatial harmonic of the unknown current, and a local maximum at v≈±50 (and, in general, at v=±1/4 a-1). Moreover, the transfer function has an exponential decay for |v|≳200, whose value tends rapidly toward zero. Although the bounded oscillations in |v|≳600 have a pseudorandom appearance, they are caused by an infinite x-domain function with a fast decay toward zero at high frequencies, which is approximated by a truncated function.
To compare the MoM and MoS!, we find the input impedance (Zin) of a center-fed dipole using the magnetic frill source simplified by
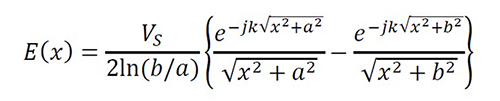 Equation 35
Equation 35
for all x∈Ω, b=2.3a and VS=1. Because the complex power provided by the source is S=1/2 ∫-L/2
L/2 E(x)I* (x)dx, and it can also be defined using S=1/2 |I(0)|2 Zin, we estimate the input impedance with the MoM using IΩ (x)~Ψ(x) as
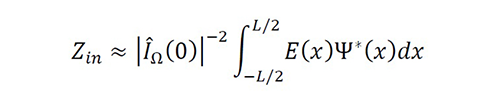 Equation 36
Equation 36
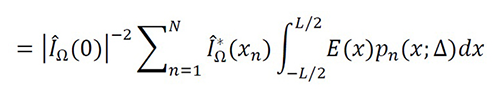 Equation 37
Equation 37
In the MoS!, any continuous operation with the unknown current requires the definition of an interpolator because Ψ(x) loses information between discrete samples. Without loss of generality, we find I ̂Ω (x) through the piecewise cubic Hermite interpolating polynomials [21] using I ̂Ω (xn) and the boundaries I ̂(±L/2)=0. Consequently, we estimate the input impedance with the MoS! by using
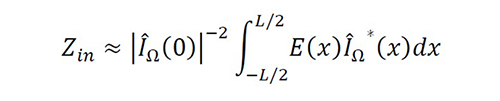 Equation 38
Equation 38
Furthermore, the difference between the MoS! and MoM is particularly accentuated when we use bandlimited interpolation functions. For instance, and only to differentiate between the methods, if p(x;Δ)=sinc(πx∆-1) with xn=-L/2+∆∙n and ∆=L/(N+1), PM-P obtains an impedance matrix (Z) with coefficients
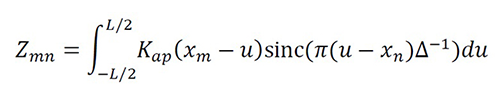 Equation 39
Equation 39
Therefore, O(N2) is required to ensure computational storage and O(N3) is required to solve the linear equation system using Gaussian elimination because the impedance matrix does not have useful properties. In contrast, the system matrix (S) obtained by (15) is a symmetric Toeplitz matrix, which only requires O(N) for computational storage, and several efficient algorithms are available to solve the linear equation system [22]. We compare Zin using PM-P and BM-P with L=0.47λ in table 1a.
Another application of the MoS! is to use the system matrix as a preconditioner for the MoM because S-1 E may lead to a low computational cost and both formulations are closely related at xm,xn∈S. As an example, figure 5 shows the relative residual error in solving ZΨ=E using sinc(∙) and the conjugate gradient squared method (CGS) with and without the preconditioner S. As shown, the solution with the preconditioner S has fast convergence, even for a small number of unknown variables (N).
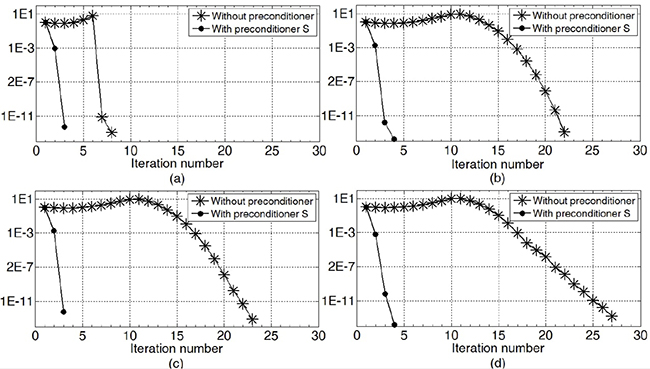 Figure 5. Relative residual error at with CGS
Figure 5. Relative residual error at with CGS
(a) N=11
(b) N=53
(c) N=95
(d) N=137
Source: Páez [8]
Although the unknown current has a well-identified fundamental harmonic at v=±1, a considerable bandwidth (BW> 1/2Δ|N=101= N+1/2L |N=101=108.5) is necessary to obtain an absolute relative error less than 3.5 % in the imaginary part. The analysis of the magnetic frill source shows that its bandwidth is the cause of this situation. If we assume that Zin is mainly obtained from band base information, filtering the source with the normalized filter RΛ (x;Δ)=Δ-1 ΛΔ (x) should increase the convergence rate, as shown in table 1b.
Table 1. Input impedance for a center-fed dipole using the interpolation function with and
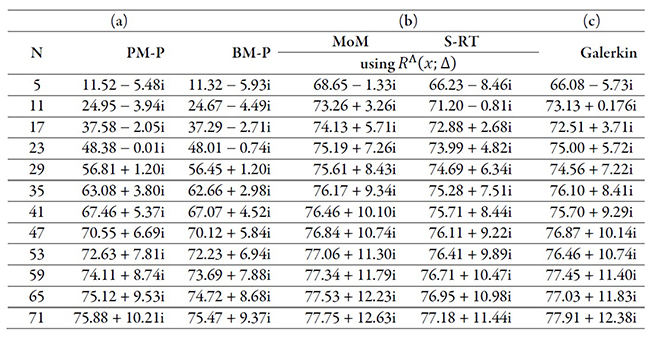
(a) Basic approach with PM-P and BM-P
(b) Subdomain regularization technique with MoM and S-RT
(c) Galerkin method (MoM)
Source: Páez [8]
We compare the results with those obtained using the Galerkin method in table 1c. According to our approach, the Galerkin method obtains an oscillatory convergence rate because filters conformed by truncated sinc functions do not have well located spectral nulls to ensure the efficient elimination of the interference.
The Zin evaluated using the ultraformulation (23)-(25) and using the v-domain (16), (26) exhibit relative residual errors that are less than 1×10-5. In particular, using the symmetric of (32), we simplify (16) and (26) using RΛ (∙) by using
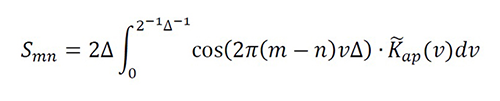 Equation 40
Equation 40
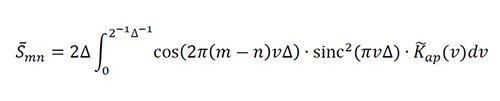 Equation 41
Equation 41
Although (40)-(41) have some disadvantages caused by the Fourier transform estimation and the evaluation of an integrand with an oscillatory behavior, they have other advantages owing to the prior theoretical knowledge of R ̃(∙) and p ̃(∙), the finite interval of integration, the use of the FFT for a fast calculation and windowing to reduce the truncation effect over K ̃ap (v). The system coefficients calculated by v-domain are a relevant option for other more convenient bandlimited interpolation functions, such as the raised cosine functions.
In conclusion, using potentially the most critical bandlimited interpolation function, we demonstrate that the MoS! is a viable alternative with low computational cost because the new matrix has useful properties based on symmetry, and it can be calculated using low cost alternative expressions. Although the MoM has a better convergence rate in this example, the solution of S ̅N+18 is mostly equivalent to Z ̅N. Moreover, we show that the system matrix can be used as a preconditioner for the MoM using a well-known Krylov subspace iterative method with very fast convergence.
Furthermore, the MoS! can simplify the solution using subdomain functions because the ultraformulation is well defined for K∈L2. For such a case, we emphasize that if Ωpn,ΩRm)⊆Ω, both matrices are equal (S=Z). However, the input impedance is different because both methods employ different approaches for the unknown continuous approximation. In this example, this difference is smaller because the input impedance is calculated using an integral operator (a low-pass operator). To discuss the ultraformulation, we first evaluated Zin in tables 2a and b using the rectangular and triangular functions with PM-P (and BM-P in the parenthesis) using (15), and MoM (and S-RT in the parenthesis) with the filter RΛ (∙) using (21). As expected, the rectangular function with BM-P exhibited an oscillatory behavior without convergence because the reduced kernel has low attenuation for its interference (see figure 4c in |v|≤50).
Because (RΛ*pΠ)(x;∆) and (RΛ*pΛ)(x;∆) have closed forms, the ultraformulation has two advantages. The first advantage is the reduction of the computational cost owing to the transformation of the 2D integral to 1D. The second advantage is the reduction of the nontrivial effects of rounding errors. In particular, (24) reduces the jitter produced between the interpolation functions and filters, and (25) reduces the jitter produced by the kernel. For instance, we note that the input impedance in table 2b using p^Π (∙) and R^Λ (∙) must lead to better performance because the kernel and the source have been filtered. Table 2c summarizes the new estimation using (24), in which we remove the lack of convergence without changing the numerical methods. We highlight this nontrivial issue because κ(SN)≤600 for N≤113.
Table 2. Input impedance for a center-fed dipole using classical subdomain functions with and
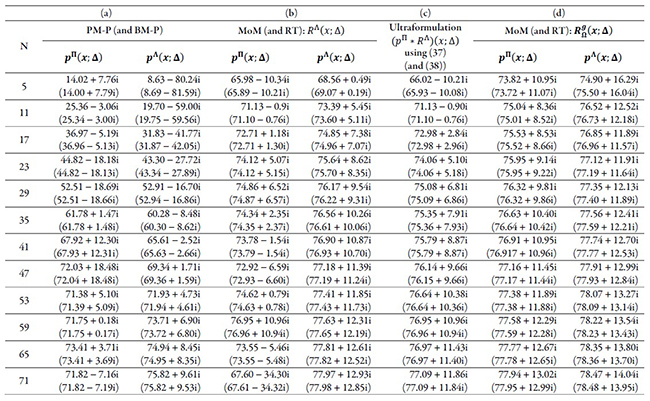
(a) Basic approach with PM-P (and BM-P)
(b) Subdomain regularization technique with MoM (and RT)
(c) Ultraformulation using (24)
(d) Entire domain regularization technique with MoM (and RT)
Source: Páez [8]
Continuing the discussion on regularization, we note that filters with subdomains are inefficient in reducing the source’s bandwidth due to the time-frequency relationship (formally, the relationship between the x and v domains). To enhance the convergence, we propose the sampled filter RΩ
g (xm-x) inspired by the standard Gaussian filter
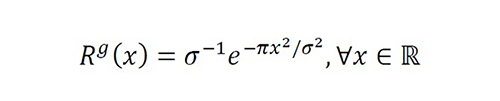 Equation 42
Equation 42
where σ=c∙∆ to obtain a nascent Delta-Dirac function (c≥1).
Table 2d shows the recalculation of Zin using the entire domain filter with c=1.5. As shown, it is possible to improve the convergence significantly, even for low order interpolation functions (e. g., tables 1 and 2 show that the triangular interpolation function with the quasi-Gaussian filter using N=17 has the same approximate performance as that of the triangular filter using N=41, without filter using N=77, and with the entire domain formulations using the sinc function and N>53). Nevertheless, some disadvantages were observed when filters were used in this problem. First, the conditioning number and the fake oscillations [23] and [24] may be increased because the filters reduce the bandwidth artificially. Second, the use of any filter includes the establishment of a particular model for the discontinuities at low sampling rates, which implies that a specific model may be used for the current at the feed point and the edges of the wire. Lastly, monotone convergence using the quasi-Gaussian filter when c≳1.5 does not occur because spectral mismatches exist in this particular problem (e.g., a relevant transience exists for N<17 and c=1.5).
In summary, we solved a classical electromagnetic problem with several new paradigms. It was noted that the limiting factor for fast convergence is the bandwidth of the printed source. Therefore, the regularization filter, and not the interpolation function, is the design challenge for a fast and numerically stable solution. Moreover, it was demonstrated that the instantaneous values obtained from the system matrix allow the solution of the problem, and less notably, Ψ(x) was considered to be an interpolator with an unnecessary high computational cost. According to our approach, the use of Ψ(x) to calculate other performance parameters based on wideband operators (e.g., vector operators) is not desirable because Ψ(x) may possess information that is not valid at high frequencies. In particular, the information obtained using the reduced kernel at high frequencies by employing any method is strictly incorrect because the real part of this kernel is an almost ideal low-pass filter with essential bandwidth BW2
Re{K_ap}≈λ-1. For these reasons, we changed the terminology of “basis functions” to “interpolation functions” because these functions do not necessarily provide basis for the unknown function following the standard algebraic approach.
Conclusions
The authors presented a novel approach to solve integral equations with difference kernels, based on the generalization of a Fredholm equation of the first kind, as an extended convolutional problem. The results demonstrated that the method of moments (and in general, the method of weighted residuals) is a particular case, in which new interpretations, degrees of freedoms and design rules can be found using standard matrix techniques.
The new approach can be used to address major methodological questions for the method of moments; these questions include those pertaining to the design of all the functions related with the computational method (e.g., to the best of the author’s knowledge, a general approach for the design of weighting functions has not been reported so far), the establishment of preconditioners in a systematic manner (e.g., in problems using bandlimited basis functions), the reduction of computational cost based on several new properties (e.g., using ultraformulation and functions with an approach that does not necessarily imply orthogonality, differentiability or smooth continuity), the use of the Fourier transform as a fundamental design tool although the solution must be performed in the original domain (e.g., via matrix coefficients calculated by the Fourier domain), and better understanding the formulation based on the interior product as a particular case of regularization using convolution.
References
A. Polyanin and A. Manzhirov, Handbook of Integral Equations. Boca Raton, FL, USA: CRC Press, 1998.
R. Garg, Analytical and Computational Methods in Electromagnetics. Boston, MA, USA: Artech House Incorporated, 2008.
M. N. O. Sadiku, Numerical Techniques in Electromagnetics with MATLAB, third edition. Boca Raton, FL, USA: CRC Press Inc., 2009.
R. F. Harrington, “Matrix methods for field problems,” Proceed. IEEE, vol. 55, no. 2, pp. 136–149, Feb. 1967.
R. F. Harrington, Field Computation by Moment Methods. New York, NY, USA: Macmillan, 1968.
Z. Chen and S. Luo, “Generalization of the finite-difference-based time-domain methods using the method of moments,” IEEE Trans.Antennas Propag., vol. 54, no. 9, pp. 2515–2524, Sept. 2006.doi: 10.1109/TAP.2006.880733
Z. Chen and M. Ney, “The method of weighted residuals: A general approach to deriving time- and frequency-domain numerical methods,” IEEEAntennas Propag.Mag., vol. 51, no. 1, pp. 51–70, Feb. 2009.doi: 10.1109/MAP.2009.4939019
C. I. Páez, “A new computational approach to solve convolutional integral equations: The method of sampling for one dimension,” Ph.D. dissertation, Univ. Andes, Bogotá, Colombia, 2017.
B. Kolundzija and B. Popovic, “Entire domain galerkin method for analysis of generalised wire antennas and scatterers,” IEE Proc.H Microw.,
Antennas Propaga., vol. 139, no. 1, pp. 17–24, Feb. 1992.doi: 10.1049/ip-h-2.1992.0004
E. Rothwell, “The transmission line as a simple example for introducing integral equations to undergraduates,” IEEE Trans.Edu., vol. 52, no. 4, pp. 459–469, Nov. 2009.doi: 10.1109/TE.2008.930507
G. Antonini and F. Ferranti, “Integral equation-based approach for the analysis of tapered transmission lines,” IETSci., Meas.Technol., vol. 2, no. 5, pp. 295–303, Sept.2008.doi: 10.1049/iet-smt:20070110
J. Goswami, A. Chan and C. Chui, “On solving first-kind integral equations using wavelets on a bounded interval,” IEEE Antennas Propag. Mag., vol. 43, no. 6, pp. 614–622, Jun. 1995.doi: 10.1109/8.387178
A. Peterson and M. Bibby, “High-order numerical solutions of the mfie for the linear dipole,” IEEE Trans.Antennas Propag., vol. 52, no. 10, pp. 2684–2691, Oct. 2004.doi: 10.1109/TAP.2004.834407
J. Tsalamengas, “Exponentially converging nystrom methods in scattering from infinite curved smooth strips: Part 1: Tm-case,” IEEE Trans.Antennas Propag., vol. 58, no. 10, pp. 3265–3274, Oct. 2010.doi: 10.1109/TAP.2010.2055788
J. Tsalamengas, “Exponentially converging nystrom methods in scattering from infinite curved smooth strips: Part 2: Te-case,” IEEE Trans.Antennas Propag., vol. 58, no. 10, pp. 3275–3281, Oct. 2010.doi: 10.1109/TAP.2010.2063412
O. Bucci and G. Franceschetti, “On the spatial bandwidth of scattered fields,” IEEE Trans.Antennas Propag, vol. 35, no. 12, pp. 1445–1455, Dec. 1987.doi: 10.1109/TAP.1987.1144024
G. Herrmann, “Note on interpolational basis functions in the method of moments [em scattering],” IEEE Trans.Antennas Propag., vol. 38, no. 1, pp. 134–137, Jan. 1990.doi: 10.1109/8.43601
F. Teixeira and J. Bergmann, “Moment-method analysis of circularly symmetric reflectors using bandlimited basis functions,” IEE Proc.Microw., Antennas Propaga., vol. 144, no. 3, pp. 179–183, Jun. 1997.doi: 10.1049/ip-map:19971109
G. Herrmann and S. Strain, “Sampling method using prefiltered band-limited green’s functions for the solution of electromagnetic integral equations,” IEEE Trans.Antennas Propag., vol. 41, no. 1, pp. 20–24, Jan. 1993.doi: 10.1109/8.210110
J. H. Richmond, “Digital computer solutions of the rigorous equations for scattering problems,” Proc. IEEE, vol. 53, no. 8, pp. 796–804, Aug. 1965.doi: 10.1109/PROC.1965.4057
F. N. Fritsch and R. E. Carlson, “Monotone piecewise cubic interpolation,” SIAM J.Numer.Anal., vol. 17, no. 2, pp. 238–246, Apr. 1980. [Online]. Available: http://dx.doi.org/10.1137/0717021
R. P. Brent, “Old and new algorithms for toeplitz systems,” Proc. SPIE, vol. 0975, pp. 2–9, 1988. [Online]. Available: http://dx.doi.org/10.1117/12.948485
G. J. Burke, “Accuracy of reduced and extended thin-wire kernels,” in The 25th Int. Rev.Prog. Appl.Comput. Electromagn.ACES 2009. Available: http://bit.ly/2XY95vc
P. Papakanellos, G. Fikioris, and A. Michalopoulou, “On the oscillations appearing in numerical solutions of solvable and nonsolvable integral equations for thin-wire antennas,” IEEE Trans.Antennas Propag., vol. 58, no. 5, pp. 1635–1644, May 2010.doi: 10.1109/TAP.2010.2044319
R. Allen and D. Mills, Signal analysis. Piscataway, NJ, USA: Wiley-IEEE Press, 2004.Available: http://dsp-book.narod.ru/SATFSS1.pdf
R. S. Strichartz, A Guide to Distribution Theory and Fourier Transforms.Boca Raton, FL, USA: CRC Press, 1994.
A. Preliminaries
A.1. Standard Functions and their Characteristics
Let be a complex-valued function. Let be a truncated function with compact support given by
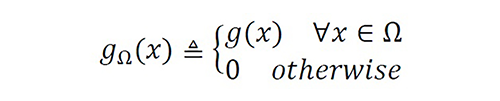 Equation 43
Equation 43
Let be the rectangular function, let be the triangular function, and let .
Let if , and let if [25]. Let and .
Definition 6. Let be a nascent Delta-Dirac function for if
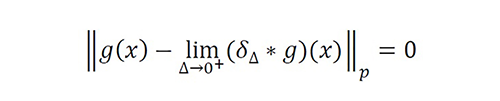 Equation 44
Equation 44
A.2. Continuous Fourier Transform
Let be the Fourier transform. If , exists.
Lemma 7.(Plancherel’s theorem) If , and .
Definition 8. The essential bandwidth of is defined by , where .
A.3. Linear System Theory
Let be a linear and invariant problem given by , where is the input, is the output, is the linear and invariant system, and is the unidimensional invariant convolution operator defined by , in the case that the improper Riemann integral is well defined. Let , in the case that the Fourier transforms , and the improper Riemann integral are well defined.
A.4. Instantaneous Sampling Theory
Let be the KroneckerDelta function. Let be the generalized Delta Diracfunction. Using the distribution theory and the generalized Fourier transform [25] and [26], the following theorems can be considered well defined:
Lemma 9. , , .
Theorem 10. Let and the uniform samples with and . The ideal instantaneous sampling theorem can be defined as
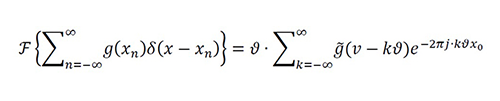 Equation 45
Equation 45
Proof.
Theorem 11. Let and the uniform samples with and . The nonideal instantaneous sampling theorem can be defined as
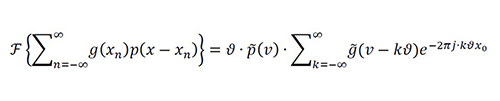 Equation 46
Equation 46
Proof.
B. Properties of Matrix B
Corollary 12. The matrix for has a theoretical inverse given by
 Equation 47
Equation 47
Corollary 13. for .
Notes
* Research article
This article is derived from the doctoral research of the first coauthor at the Universidad de los Andes, Colombia. That study was partially financed by the Plan de Formación Permanente del Profesor Javeriano (PFPP) from Pontificia Universidad Javeriana, Colombia.
How to cite this article:
C.I.Páez Rued a, andR. Bustamante Miller,“Novel computational approach to solve convolutional integral equations: Method of sampling for one dimension,” Ing. Univ.,vol. 23, no. 2,2019. https://doi.org/10.11144/Javeriana.iyu23-2.ncas
Author notes
a Autor de correspondencia. Correo electrónico paez.carlos@javeriana.edu.co