Introduction
Throughout human history, the use of fossil fuels has been the main driver of energy supply. However, the excessive use of these fuels has led to an increase in environmental pollution and a considerable decrease of them [1]. Given this, the scientific community has increased the search of renewable and sustainable sources of energy. Biomass is a renewable energy source that is currently being used as energy through various processes (gasification, combustion, pyrolysis, among others) to obtain higher value-added fuels.
Biomass is found in large quantities, there are various types: municipal waste, agricultural waste, animal waste, energy crops, among others. Biomass can be used for direct burning, thus providing thermal energy in the required locations, however, direct combustion thereof causes environmental impacts due to polluting emissions such as CO2 or nitrous oxides, when the temperature of the products reaches relatively high values, these components are harmful to health and life on the planet. As an alternative to biomass combustion, gasification emerges as a promising technology, in which fuel gases with low calorific value are obtained for use in other applications. The advantage of gasification over combustion is the reduction of polluting emissions, since the process temperature does not reach values as high as those obtained in combustion, given that the amount of oxidizing agent is lower.
Gasification is the thermochemical process by which a carbon substrate is transformed by partial oxidation into a combustible gas containing, among other compounds, H2, CO, CH4, CO2, and N2, as well as various impurities or pollutants. The gas obtained allows its use in various current combustion machines, among which are internal combustion engines, turbines for electricity production, boilers, combustors, among others. It can also be used for the synthesis of higher value-added products [2].
Given the advantages of gasification, several authors have developed the process modeling in order to identify the characteristics of the process, while studying those variables that may affect it.
Several models have been developed in this topic; however, this work makes relevance on the models in chemical equilibrium, which allow predicting the greater composition that the process can reach under given operational conditions.
Jarungthammachote and Dutta [3], developed a chemical equilibrium model for a downdraft fixed bed gasifier, the authors use municipal solid waste as raw material, the model is used to analyze the effect of biomass moisture on the process, and is validated with the results published by various authors, also, the model is analyzed according to the second law of thermodynamics.
A similar work was developed by Melgar et al. [4], in their model the authors establish that the overall reaction of gasification with air includes the products CH4, H2O, N2, CO, CO2, H2, SO2 and O2, the influence of the air-fuel ratio is investigated, as well as the moisture content on the process, assuming sufficient residence time to reach equilibrium and that all the carbon present in the biomass has been gasified, the model is validated with the data published by Jayah [5].
Khadse et al. [6] developed a model for predicting Syngas from the biomass gasification process in an updraft fixed bed reactor by thermochemical equilibrium. Biomass expressed as CHxOy, reacts with water steam and air to obtain a gas whose composition presents CO, CO2, H2 and CH4. The model equations contain four atomic balances (C, O, H and N) and the relationships between the equations are solved using MATLAB. This model compares the gas concentration obtained for four types of biomass from India. A similar model was developed by Melgar et al [4]. Similarly, Mendiburu et al. [7] developed four models in thermochemical equilibrium based on empirical correlations using published experimental data, the authors validated their work with the data published by Jayah et al. [5]. On the other hand, other authors [8], [9], [10], [11], developed equilibrium models through the implementation of commercial software, whose advantage lies in the speed of their calculation, which at the same time allows the implementation of other variables that are not considered in the mathematical models due to their complexity. One of the software frequently used to study the gasification process is Aspen Plus; this software consists of a series of work blocks that allow simulating the stages that occur in the gasification.
The model developed with this work tries to predict with great similarity the gas concentrations of CH4, H2O, N2, CO, CO2, H2, and will be a basis for future work in greater detail. The model is developed under the chemical equilibrium, the biomass used is oil palm kernel with established characteristics. The model determines the amount of air needed for the development of the process. For solving the equations, the EES software was used since the system is a non-linear system.
Materials and methods
Initially, there is a brief description of the stages that occur in the gasification process in a fixed bed downdraft reactor, the considerations used for the calculation of the thermodynamic properties of the necessary components are shown, as well as the equations used; subsequently, the energy balance of the process is shown according to the first law of thermodynamics, followed by the parameters used to estimate the Gibbs energy of the compounds in the gasification process.
The Figure 1 shows the structure used for the development of the equilibrium model, then a description is made of the equations used and the calculations developed.
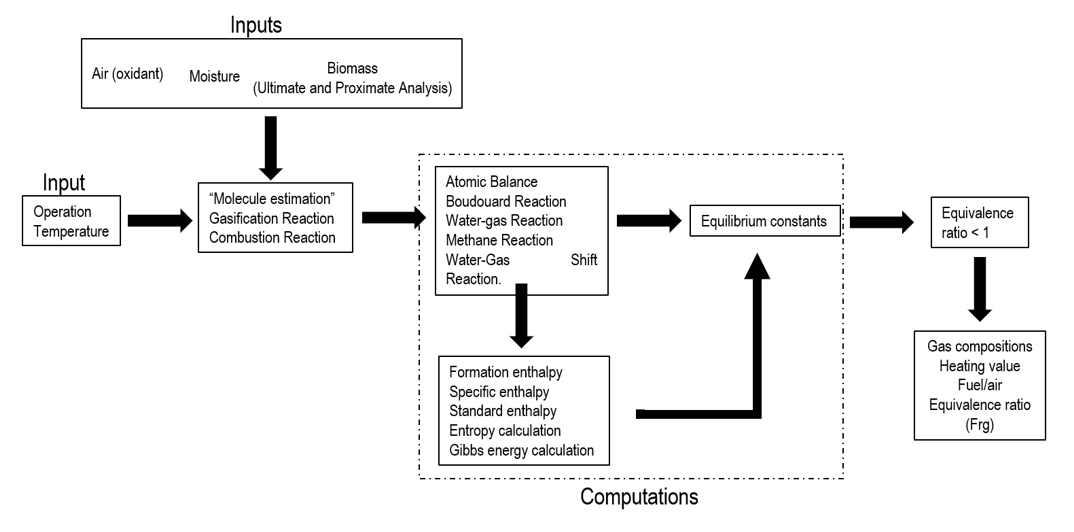 Figure 1.
Structure of the simulation equilibrium model
Figure 1.
Structure of the simulation equilibrium model
Source: Authors own elaboration.
The Figure 2 shows the stages of the gasification process for a downdraft fixed bed reactor.
The reactions that the material to be gasified undergoes when it comes into contact with the oxidizing agent and the energy released determine the gasification zones.
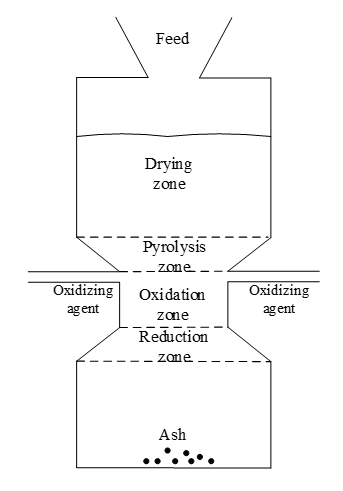 Figure 2.
Zones of the gasification process in a downdraft fixed bed reactor
Figure 2.
Zones of the gasification process in a downdraft fixed bed reactor
Source: Adapted from [12].
The first stage of the process corresponds to the drying stage, whose typical temperature is around 100 to 200 ºC. Conversion takes place due to heat transfer between the hot gases in the oxidation zone [13]. Following the drying stage, the pyrolysis zone is presented, which takes place when the biomass reaches a temperature between 200 and 600 ºC and which is responsible for the thermal decomposition of the material in the absence of air to produce volatile, charcoal and condensable vapors of high and medium molecular weight called tars [14].
The reaction that occurs at the pyrolysis stage can be expressed as shown in equation 1.
After the pyrolysis stage, the oxidation zone is presented, which provides the energy in the form of heat released by oxidizing the biomass, so that the drying, pyrolysis and other endothermic reactions develop during the reduction. In the latter, carbon dioxide and water are reduced to form carbon monoxide and hydrogen; more complex reactions also appear [14].
Parameter development and estimation
The biomass used in the process corresponds to oil palm kernel, the characteristics of it, are presented in Table 1, in this the term HHV refers to the higher heating value of biomass.
Table 1.
Elemental and proximate analysis of the biomass used
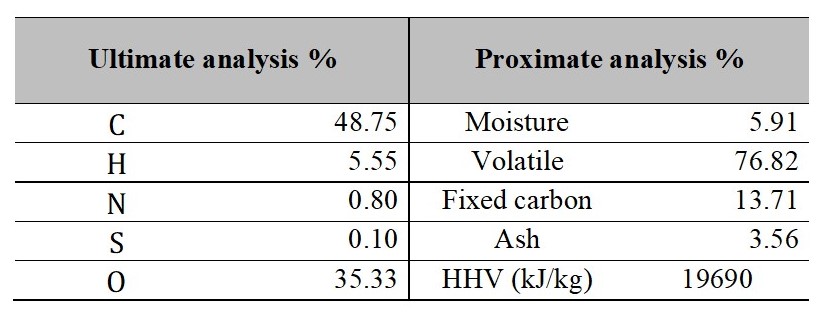
Source: Authors own elaboration.
The analysis begins with the formulation of the general equation of biomass gasification (Equation 2) as reported by [3], the presence of sulfur has been ignored in order to reduce complexity in the calculations, as well as the formation of tar, the molecule CH
x
O
y
N
z is formed from the coefficients x, y, z, which are estimated by equations 3, 4 and 5 respectively.
Where H, N, C, O are the percentages given by the ultimate analysis, M represents the molar mass of each element in
kg/kmol
. According to this, the molecule CH
1.366
O
0.544
N
0.014 is obtained.
From equation 2, w, a, x1, x2, x3, x4 and x5 represent the number of moles of each component
( z 2 + 3 . 7 6 a )
, corresponds to the number of moles of N
2 in the reaction.
The moles of water in the reagents can be estimated using the following equation:
From the proximate analysis the %moisture is obtained, when clearing from the previous equation the following is obtained:
The atomic balance for the reaction of equation 2 corresponds to:
Carbon balance.
Hydrogen balance.
Oxygen balance.
Nitrogen in equation 2 is balanced.
Since it is necessary to solve the system of previous equations, it is necessary to specify three additional equations because there are six unknowns (a, x1, x2, x3, x4 y x5). Two of these equations are provided by the following reactions according to what is stated by [3]-[4].
Boudouard reaction.
Water-gas reaction
Methane Reaction
The reactions (Equations 11 and 12) can be combined to obtain the Water-Gas Shift reaction.
The equilibrium constants have to be calculated for the reactions given by equations 13 and 14 respectively, according to [3]-[4].
Where K
13 and K
14 refer to the equilibrium constants of the reactions shown in equations 15 and 16 respectively, in these equations, 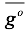 is the Gibbs energy, R is the ideal gas constant, and T is the temperature.
is the Gibbs energy, R is the ideal gas constant, and T is the temperature.
Energy balance according to the first law of thermodynamics
In this model, it is assumed that reagents enter at standard conditions (25ºC and 1.0 atm) and that the products come out at an assumed temperature T (773K) and 1.0 atm, in order to give a solution thereof. Figure 3 shows a general diagram of the energy balance.
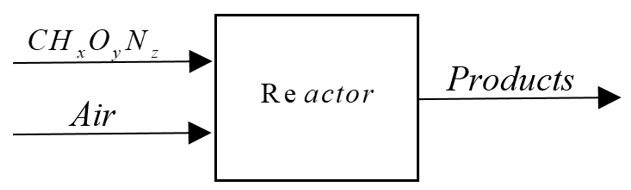 Figure 3.
General diagram of the energy balance for a reacting system
Figure 3.
General diagram of the energy balance for a reacting system
Source: Authors own elaboration.
The energy balance for a stationary flow system based on the first law of thermodynamics for a reacting system is given by:
For the case presented here, the above equation is expressed as:
Where 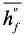 is the enthalpy of formation,
is the enthalpy of formation, 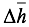 is the change of enthalpy, n
R and n
p represent the moles of the reagents and the products respectively.
is the change of enthalpy, n
R and n
p represent the moles of the reagents and the products respectively.
The enthalpy of formation for the known elements is shown in Table 2. These values correspond to those reported in [15].
Table 2.
Enthalpy of formation for common components

Source: [15].
The enthalpy of formation for the fuel is calculated according to that published by Souza Santos [16]
Where corresponds to the enthalpy of formation of the products under the premise of complete combustion (Equation 20).
From the balance of this equation, the values for a
th = 1.0695, b = 1, d = 0.683, e = 4.02832 are obtained.
For an initial estimate of the enthalpy of formation of the fuel, the value of the 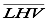 (on molar base) is approximated as the value provided by the laboratory analysis, this corresponds to a value of 438417.54 kJ/kmol.
(on molar base) is approximated as the value provided by the laboratory analysis, this corresponds to a value of 438417.54 kJ/kmol.
In this way, the enthalpy of formation of the fuel corresponds to:
Enthalpy at specific and standard temperature for reagents and products
Under the established by [3], the calculation of enthalpy is carried out by means of equation 22, the coefficients thereof are shown in Table 3, here 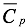 is the specific heat.
is the specific heat.
Table 3.
Coefficients for determining enthalpy by equation 21
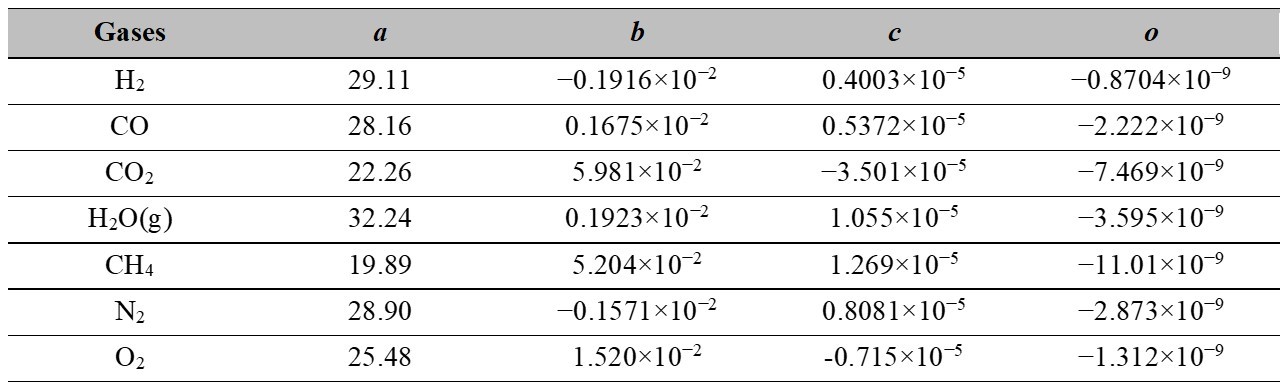
Source: [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15].
The calculated values as well as other data of interest are shown in Table 4.
Table 4.
Values at T and To
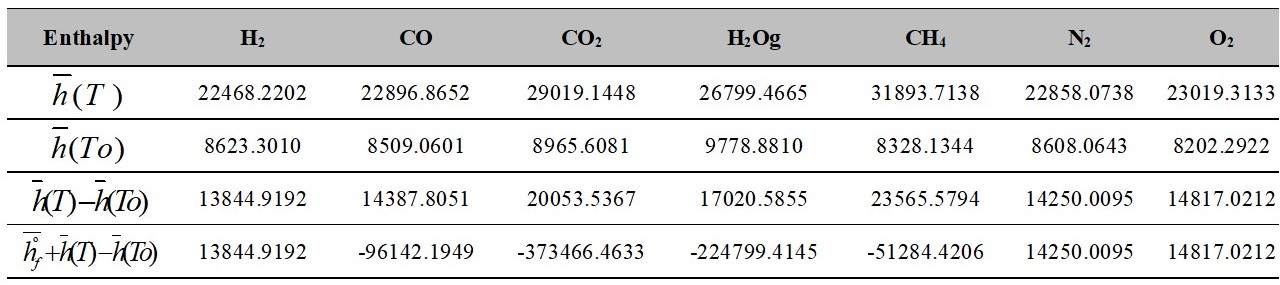
Source: Authors own elaboration.
In this way, when expressing equation 18 with the values of the enthalpies, we have:
Gibbs energy calculation
According to equations 15 and 16, it is necessary to calculate the Gibbs energy (Equation 24) in order to find the equilibrium constants.
In order to do this, it is necessary to calculate the entropy at temperature T of the products and a To of the reagents. The entropy can be calculated by equation 25 according to the established by [15].
Where 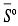 corresponds to standard entropy. Table 5 summarizes the entropy values found.
corresponds to standard entropy. Table 5 summarizes the entropy values found.
Table 5.
Values of S0 and ΔS0 at T and To (T = 773 K)
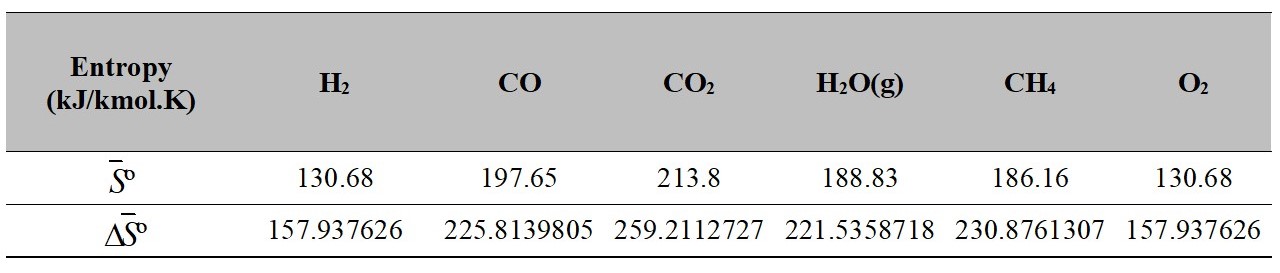
Source: Authors own elaboration.
With these values, we proceed to find the Gibbs energy values (Table 6) for the components of interest, which allow finding the constants K
13 and K
14, thus completing the system of non-linear equations.
Table 6.
Values of g0 (for T = 773 K)

Source: Authors own elaboration.
Results
The mole fractions of the gases obtained through temperature variation and equivalence ratio (ER) are shown, as well as the calculation of the lower heat value (LHV) and its behavior with temperature increase.
Products molar concentration
Figure 4 shows the mole fraction of the gases with the increase in process temperature, while Figure 5 shows the behavior with respect to the equivalence ratio.
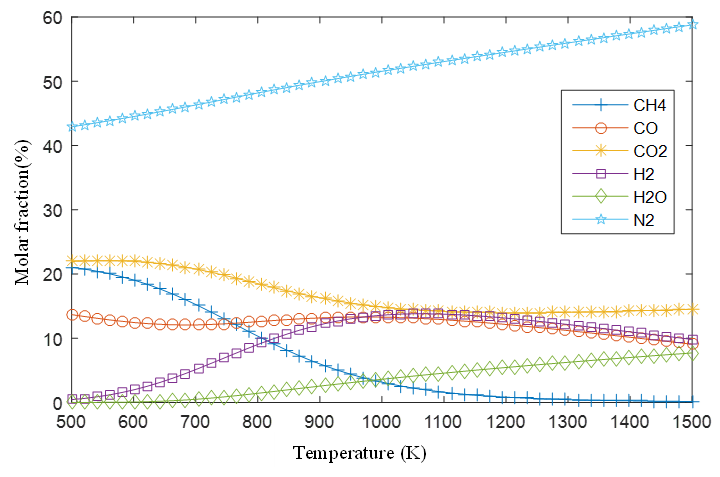 Figure 4.
Products mole fraction with temperature variation
Figure 4.
Products mole fraction with temperature variation
Source: Authors own elaboration.
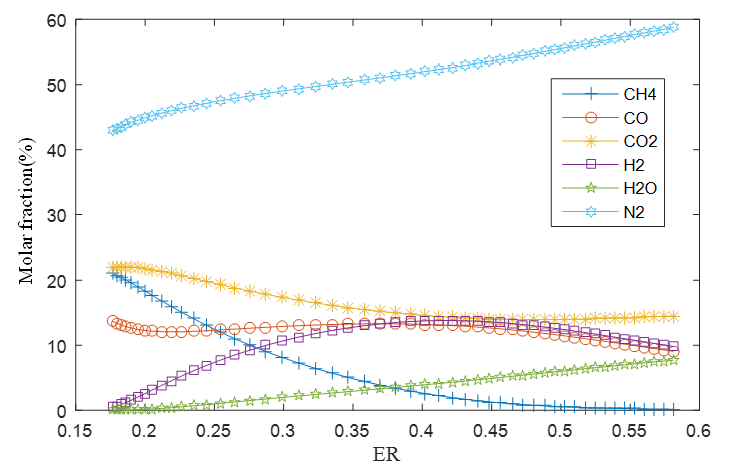 Figure 5.
Product molar ratio with variation of equivalence ratio (ER)
Figure 5.
Product molar ratio with variation of equivalence ratio (ER)
Fuente: Authors own elaboration.
Calculation of the LHV of the product gases
The lower calorific value of the gas is estimated from the gas concentration, using equation 26, taken from [17].
Equation 26 corresponds to the mole fraction of the gases.
Figure 6 shows the values obtained for the LHV of the product gases for temperature values in the range 500 K to 1500 K.
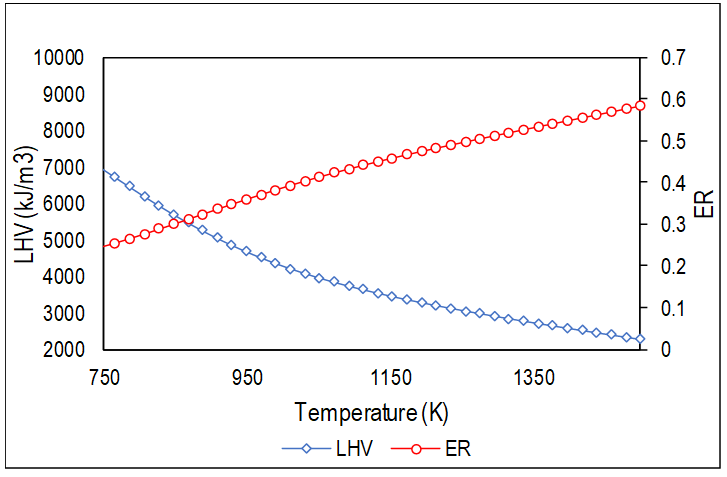 Figure 6.
Behavior of the LHV with temperature variation.
Figure 6.
Behavior of the LHV with temperature variation.
Source: Authors own elaboration.
Figure 6 shows the behavior of the calorific value of the gas obtained when varying the outlet temperature of the products, which indicates that in a real process if the temperature increases, while maintaining the biomass flow constant, the source of the rise in temperature is due to a higher amount of oxidant entering the reactor, which causes the process to get close to a combustion process and, therefore, less combustible gases are generated. Typical values of LHV in a fixed bed reactor that uses air as an oxidizing agent are in the range of 3 to 6 MJ/m3.
Model validation
The model results have been compared with those obtained by Huan et al. [18], Altafini et al. [19], Paviet et al. [9] and by Melgar et al. [4] for the conditions established by these (Table 7). Figures 7, 8, 9, and 10 show the results obtained.
Table 7.
Operation conditions Huan et al. [18]; Altafini et al. [19]; Paviet et al. [9] ;Melgar et al. [4]
![Operation conditions Huan et al. [18]; Altafini et al. [19]; Paviet et al. [9] ;Melgar et al. [4]](47762366005_gt9.png)
Source: Authors own elaboration.
![Model results compared with Altafini et al. [19]](47762366005_gf8.png) Figure 7.
Model results compared with Altafini et al. [19]
Figure 7.
Model results compared with Altafini et al. [19]
Source: Authors own elaboration.
![Model results compared with Huan et al. [18]](47762366005_gf9.png) Figure 8.
Model results compared with Huan et al. [18]
Figure 8.
Model results compared with Huan et al. [18]
Source: Authors own elaboration.
![Model results compared with Melgar et al. [4]](47762366005_gf10.png) Figure 9.
Model results compared with Melgar et al. [4]
Figure 9.
Model results compared with Melgar et al. [4]
Source: Authors own elaboration.
![Model results compared with Melgar et al. [4]](47762366005_gf11.png) Figure 10.
Model results compared with Melgar et al. [4]
Figure 10.
Model results compared with Melgar et al. [4]
Source: Authors own elaboration.
Figures 7, 8, 9, and 10 show the mole fractions of the gas composition obtained by direct comparison with the results reported by Altafini et al. [19], Huang et al. [18], Paviet et al. [9] and Melgar et al. [4]. The composition of the gas is about 21% off from that reported by the authors (except for CH4, which exceeds this percentage); this trend is shown in Figure 7, in which the mole percent of the gases obtained are further off. However, starting from figures 8, 9 and 10, the model fits adequately to the values reported by Huan et al. [18], Paviet et al. [9], and Melgar et al. [4], which shows that the work developed is a good tool for the initial prediction of the gas obtained by fixed bed gasification using air as oxidant.
Conclusions
A model in chemical equilibrium has been developed for the gasification of palm oil kernel by means of the software EES, this type of models allows obtaining the greater composition that could be obtained when the biomass is gasified, in this case the oxidizing agent used is air.
The maximum temperature for the gasification process in a fixed bed reactor is around 800 °C to 1500 ºC, in this work the maximum temperature of the reactor has been varied from 500 to 1500 K in order to observe its influence on the parameters of interest, the temperature has been the input value to the model for solving the system of non-linear equations obtained.
The lower calorific value for fixed bed gasification with oxidizing air ranges from 1.0 to 6.0 MJ/m3; these values are obtained for temperatures from 900 to 1500 K.
The model adequately predicts the compositions of CO, H2, CO2, and N2 with values close to those reported in the literature, while the estimate of CH4 in some cases is overestimated and underestimated, something characteristic in equilibrium models, this is the main limitation of the proposed model, which must be considered and adjusted in future work.
References
[1] M. Bassyouni et al., “Date palm waste gasification in downdraft gasifier and simulation using ASPEN HYSYS,” vol. 88, pp. 693–699, 2014.
[2] G. García, “Estudio experimental de la cogasificación de fangos de EDAR y carbón con aire en lecho fluidizado,” tesis, Universidad de Zaragoza, España, 2013.
[3] S. Jarungthammachote and A. Dutta, “Thermodynamic equilibrium model and second law analysis of a downdraft waste gasifier,” Energy, vol. 32, no. 9, pp. 1660–1669, 2007.
[4] A. Melgar, J.F. Pérez, H. Laget, and A. Horillo, “Thermochemical equilibrium modelling of a gasifying process,” Energ. Convers. Manage., vol. 48, no. 1, pp. 59–67, 2007.
[5] T.H. Jayah, L. Aye, R.J. Fuller, and D.F. Stewart, “Computer simulation of a downdraft wood gasifier for tea drying,” Biomass Bioenergy, vol. 25, no. 4, pp. 459–469, 2003.
[6] A. Khadse, P. Parulekar, P. Aghalayam, and A. Ganesh, “Equilibrium model for biomass gasification.” Proceedings of the 1st National Conference on Advances in Energy Research (AER-2006), December 4-5, 2006-ISBN 9780230630062.
[7] A.Z. Mendiburu, J.A. Carvalho, R. Zanzi, C.R. Coronado, and J.L. Silveira, “Thermochemical equilibrium modeling of a biomass downdraft gasifier: Constrained and unconstrained non-stoichiometric models,” Energy, vol. 71, pp. 624–637, 2014.
[8] A. Gagliano, F. Nocera, M. Bruno, and G. Cardillo, “Development of an Equilibrium-based Model of Gasification of Biomass by Aspen Plus,” Energy Procedia, vol. 111, pp. 1010–1019, 2017.
[9] F. Paviet, F. Chazarenc, and M. Tazerout, “Thermo chemical equilibrium modelling of a biomass gasifying process using ASPEN PLUS,” Int. J. Chem. React. Eng., vol. 7, p. A40, 2009.
[10] N. Ramzan, A. Ashraf, S. Naveed, and A. Malik, “Simulation of hybrid biomass gasification using Aspen plus : A comparative performance analysis for food , municipal solid and poultry waste,” Biomass Bioenergy, vol. 35, no. 9, pp. 3962–3969, 2011.
[11] M. Fernandez-Lopez, J. Pedroche, J.L. Valverde, and L. Sánchez-Silva, “Simulation of the gasification of animal wastes in a dual gasifier using Aspen Plus??,” Energy Convers. Manag., vol. 140, pp. 211–217, 2017.
[12] M. La Villetta, M. Costa, and N. Massarotti, “Modelling approaches to biomass gasification: A review with emphasis on the stoichiometric method,” Renew. Sustain. Energy Rev., vol. 74, no. November 2016, pp. 71–88, 2017.
[13] A.A.P. Susastriawan, H. Saptoadi, and Purnomo, “Small-scale downdraft gasifiers for biomass gasification: A review,” Renew. Sust. Energ. Rev., vol. 76, pp. 989–1003, 2017.
[14] C.A. Estrada Martínez, “Modelado unidimensional y multipartícula del proceso de gasificación de biomasa lignocelulósica en una planta industrial,” tesis doctoral, Universidad de Valladolid, España, 2015 [online]. Available: https://pdfs.semanticscholar.org/7c12/c43242917ae6315d42a26e0f09a6be81c2ec.pdf
[15] Y. A. Cengel and M. E. Boles, Termodinamica-Cengel, 7th. México: McGrow Hill, 2011.
[16] Marcio L. de Souza-Santos, Solid Fuels Combustion and Gasification, 2nd ed. New York: CRC Press, 2010.
[17] P. Kuo, W. Wu, and W. Chen, “Gasification performances of raw and torrefied biomass in a downdraft fixed bed gasifier using thermodynamic analysis,” Fuel, vol. 117, pp. 1231–1241, 2014.
[18] H.J. Huang and S. Ramaswamy, “Modeling biomass gasification using thermodynamic equilibrium approach,” Appl. Biochem. Biotechnol., vol. 154, no. 1–3, pp. 193–204, 2009.
[19] C.R. Altafini, P.R. Wander, and R.M. Barreto, “Prediction of the working parameters of a wood waste gasifier through an equilibrium model,” Energy Convers. Manag., vol. 44, no. 17, pp. 2763–2777, 2003.
Notes
*
Research article
Author notes
a orresponding author. Email: daquinteroc@ufpso.edu.co
Additional information
How to cite this article: D. A. Quintero-Coronel, E. E. Espinel-Blanco, and E. N. Flórez-Solano, “Development of a chemical equilibrium model of the downdraft fixed bed gasification process with known product temperature, using air as an oxidizing agent,” Ing. Univ., vol. 24, 2020. https://doi.org/10.11144/Javeriana.iyu24.dcem







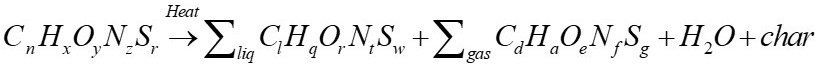 (1)
(1)
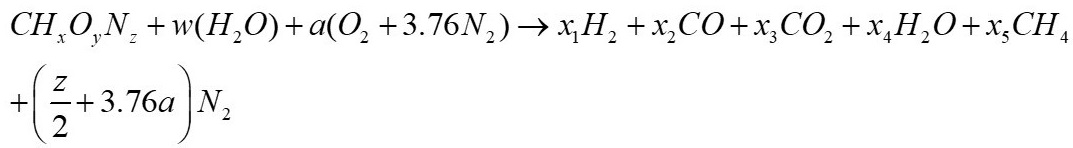 (2)
(2)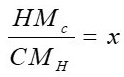 (3)
(3)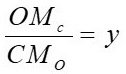 (4)
(4)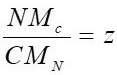 (5)
(5)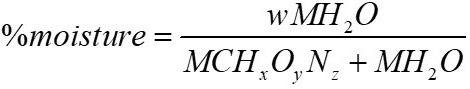 (6)
(6)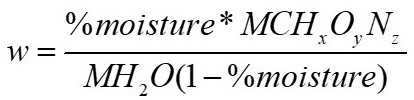 (7)
(7)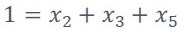 (8)
(8)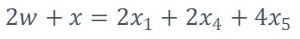 (9)
(9)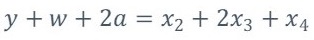 (10)
(10)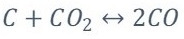 (11)
(11) (12)
(12)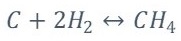 (13)
(13) (14)
(14)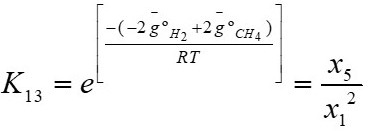 (15)
(15)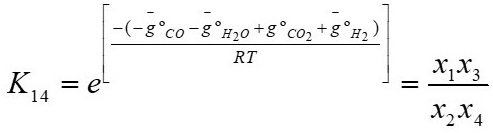 (16)
(16) is the Gibbs energy, R is the ideal gas constant, and T is the temperature.
is the Gibbs energy, R is the ideal gas constant, and T is the temperature.
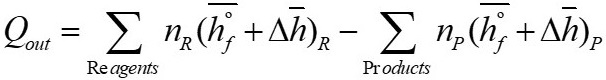 (17)
(17)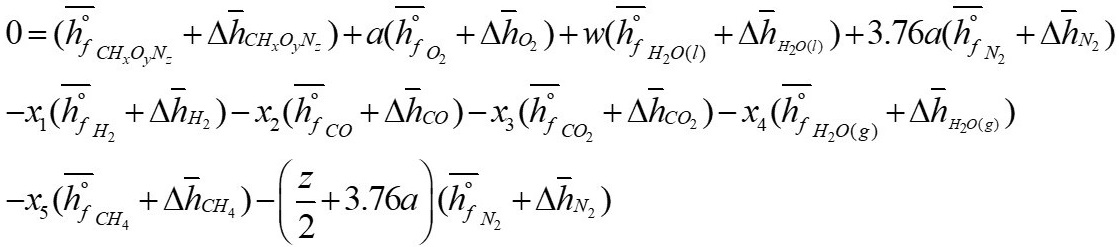 (18)
(18) is the enthalpy of formation,
is the enthalpy of formation,  is the change of enthalpy,
is the change of enthalpy, 
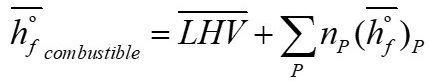 (19)
(19)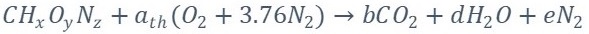 (20)
(20)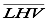 (on molar base) is approximated as the value provided by the laboratory analysis, this corresponds to a value of 438417.54 kJ/kmol.
(on molar base) is approximated as the value provided by the laboratory analysis, this corresponds to a value of 438417.54 kJ/kmol.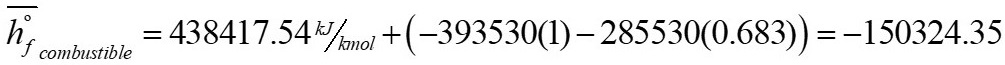 (21)
(21)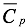 is the specific heat.
is the specific heat.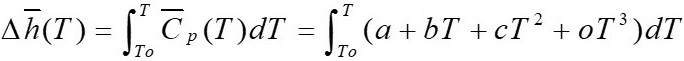 (22)
(22)

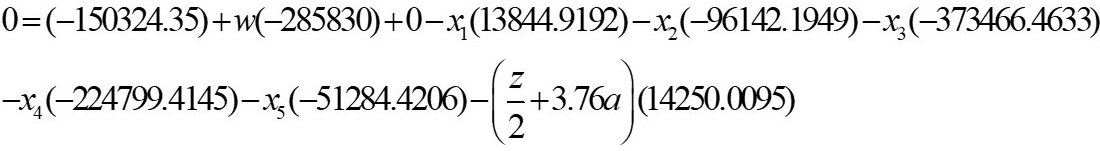 (23)
(23)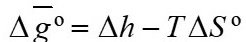 (24)
(24)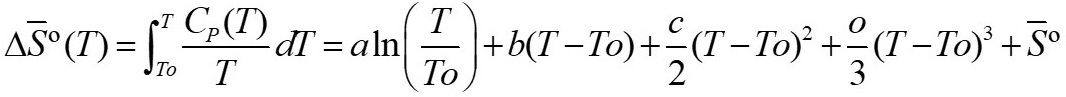 (25)
(25)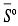 corresponds to standard entropy.
corresponds to standard entropy. 



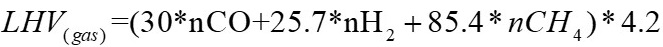 (26)
(26)
![Operation conditions Huan et al. [18]; Altafini et al. [19]; Paviet et al. [9] ;Melgar et al. [4]](47762366005_gt9.png)
![Model results compared with Altafini et al. [19]](47762366005_gf8.png)
![Model results compared with Huan et al. [18]](47762366005_gf9.png)
![Model results compared with Melgar et al. [4]](47762366005_gf10.png)
![Model results compared with Melgar et al. [4]](47762366005_gf11.png)
