Introduction
On an industrial level, the problem of batch assignment is critical. It directly impacts the delay to deliver the finished product, affecting the costs and therefore, the profits. To address this problem, we cover the case of the world’s leading company in the design and manufacturing of curved armored glass for transportation purposes. AGP group was founded 50 years ago and currently has manufacturing operations in Peru, Colombia, and Brazil. It exports specialized armored glass to more than 1000 customers in 50 countries around the world. The AGP factory in Colombia is the second oldest in the group, founded in 1989. It specializes in safety glasses with high levels of ballistic protection for cars.
The manufacturing process of armored glass goes through several phases: cutting of the glass, vitrification, bending, polishing, assembly, and lamination. The problem addressed in this document focuses on the bending phase, which is critical for AGP because of its complexity, required time, constrained capacity, and the number of furnaces available for processing.
Problem Description
The bending phase in AGP consists in passing the glass pieces through furnaces. The effect of temperature gives them the required curved shape. In this phase, batches (groups of pieces with similar characteristics), are put into the furnaces. It is in this process where the complexity of the existing AGP planning problem lies, since pieces must be assigned to batches and batches to furnaces at a specific date (as we will show later, we only assign batches to a date without considering the actual sequence of batches within the furnaces). The objective is to optimize the planning of batches, maximizing the efficiency of the furnace usage and minimizing the tardiness in delivery of orders.
Every day AGP receives orders from its customers; an order contains one or several glass pieces.
The planning process consists of:
-
Assigning the pieces to batches (a batch is a group of pieces that are going to be processed together in a furnace).
-
Assigning each batch created to a furnace and a processing date.
An order is a set of glass pieces that have to be delivered at the same time. Note that although the pieces of a given order have to be delivered together to the customer, they can be processed in different batches.
The figure 1 illustrates an example of the problem of programming AGP’s daily production.
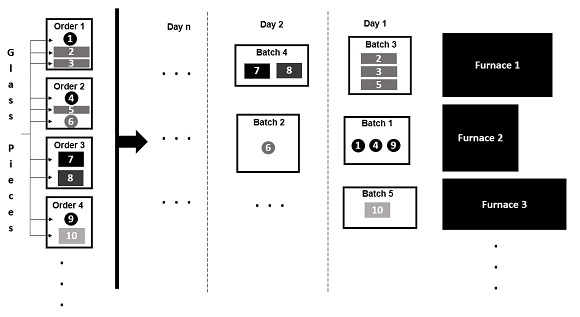 Figure 1.
Graphic representation of the bending process in AGP
Figure 1.
Graphic representation of the bending process in AGP
Source: Own elaboration
Figure 1 illustrates the batch assignment decision process. On the left side, a set of orders are received by AGP, each order consists of some number of pieces. In order to give a better explanation, we assume 10 pieces and 4 orders just as shown in figure 1. To assign pieces to batches, this case shows that pieces 1, 4, and 9 respect the constraints, and therefore are assigned to the same batch. Taking into account the features of the pieces in the batches, each piece is assigned to an appropriate furnace and to a processing day.
It is important to emphasize that in our problem we do not directly address the determination of batch sequences in the furnaces. Instead, we consider that each furnace is available during a certain amount of time per day (capacity expressed in hours). The problem is assumed to be feasible as long as the total processing time of the batches assigned to a furnace is less than its capacity. This assumption is structural as it simplifies the problem from a combination of a scheduling and a batch assignment problem to just a batch assignment problem.
This simplification is justified by the fact that the focus of the company was to address specifically the batch assignment part with all its features. Modeling all the scheduling constraints would be too complex and would have hindered the possibility of taking into account all the particularities that we wanted to address. However, in future works it would be interesting to expand the model to include more accurately the scheduling constraints.
Taking this into account, the general constraints that are considered for the development of the problem are:
-
Each order has a delivery date to the customer.
-
An order is ready when all its pieces have been processed.
-
An order may be finished after the planned delivery date, but it would mean a tardiness that penalizes the objective function.
Specific characteristics of the glass pieces need to be considered (piece width, piece class, and piece ballistic level), as well as compatibility constraints between them for the creation of batches; that means, only pieces with similar processing characteristics could be assigned to the same batch.
On the other hand, the following are the constraints considered for arranging the batches:
-
Pieces of different characteristics in a batch cannot be mixed. In particular, ballistic level and class are associated to each piece. Within a batch the maximum difference in the ballistic level of two pieces is 1 and the classes of the pieces must be the same.
-
If a piece of the batch cannot enter into the furnace because of its characteristics, the batch cannot be assigned to that furnace.
-
The width of a batch is equal to the sum of the widths of all pieces that compose it.
-
A batch can be assigned to a furnace only if its width is less than or equal to, the width of the furnace. This is because the pieces of a batch are simultaneously processed in the furnace.
-
There is no minimum or maximum limit on the number of batches that are created. However, no more batches can be created than the total quantity of pieces.
Regarding the furnaces, each one has specific characteristics, as well as different processing times and daily work capacity.
The optimization criteria identified for AGP are:
-
Minimizing usage hours of the furnaces (these hours are weighed according to an importance criterion defined by the company)
-
Minimizing tardiness delivery of orders
These criteria are strictly hierarchical. The company considers that criteria 1 is more important than criteria 2. As shown later in the document, this priority is translated in the objective function by setting a significative higher weight to criteria 1.
Based on this, we implemented a solution technique divided in two parts. The first one is a heuristic to find an initial solution. Secondly, the initial solution is complemented and improved with a Tabu Search metaheuristic. The detailed explanation of these methods will be further addressed in this document.
Literature Review
Production planning is one of the most important processes within a manufacturing company. The main goal is to determine how much to produce during a specific planning horizon in order to fulfill the demands for different time periods. Therefore, it is important to develop tools or methods that facilitate production planning decisions according to the specific features of the production process of a company.
The problem at hand can be classified as a Batch Processing Machines (BPMs) problem, with parallel non-identical machines and incompatible job families. Brucker, Mikhail and Shafransky [1] studied a two parallel, identical BPMs with unit processing times, unit set-up times, and a common deadline. Authors proved the NP-hard nature of such type of problems. Several studies address tardiness-based scheduling objectives on parallel batch processing machines. For example, Mönch, Balasubramanian and Fowler [2] proposed two different decomposition approaches based on the utilization of a genetic algorithm for minimizing total weighted tardiness on a parallel batch machines problem with incompatible job families and unequal ready times of the jobs. Chiang, Cheng and Fu [3] proposed a memetic algorithm for the identical parallel batch machines with incompatible job families and dynamic job arrival problem. Klemmt et al. [4] proposed a MIP model and a Variable Neighborhood Search (VNS) for minimizing total weighted tardiness on a parallel identical BPMs problem with different machine capacities, incompatible job families and unequal job ready times. Bilyk Mönch and Almeder [5] proposed a VNS and a Greedy Randomized Adaptive Search Procedure (GRASP) to minimize the total weighted tardiness on a parallel identical BPMs problem considering incompatible job families with precedence constraints. Gokhale and Mathirajan [6] developed certain heuristic algorithms for the parallel BPMs problem with unequal release times, incompatible job families, non-identical job sizes, heterogeneous batch processors, and allowance for job splitting with the objective of minimizing total weighted tardiness. Amouie [7] tackled the same problem with a heuristic based on column generation and a Differential Evolution (DE) metaheuristic. Moreover, Hulett, Damodaran and Amouie [8] addressed the non-identical parallel batch processing machines problem to minimize total weighted tardiness using particle swarm optimization. Finally, Lozano and Medaglia [9] proposed a two-phase hybridization of linear optimization methods and heuristics for a relaxed version of the problem at hand.
It is important to outline that, to the best of our knowledge there was no literature available that considers the BPMs problem with the non-identical and incompatible job families features together.
Mathematical Formulation
In this section we model our problem as a Mixed Integer Program. As far as we know and given the specific features of our problem, such an MIP formulation is not mentioned in the literature. Although the model will not be used to solve our problem (as shown later, the size of the problem prevents using an exact approach) an MIP formulation helps to understand in more details the decisions and constraints of the problem. The notation used in the formulation is presented below.
𝑊𝑡𝑎𝑟𝑑𝑖𝑛𝑒𝑠𝑠 and 𝑊𝑓𝑢𝑟𝑛𝑎𝑐𝑒𝑠 are the prioritization established by AGP for each of the parts that make up the objective function.
Objective Function
Subject to
The objective function (1) minimizes the usage hours of the furnaces and tardiness. Constraint set (2) ensures that each piece is assigned to one batch. Constraint set (3) ensures that a batch cannot be assigned to more than one furnace and more than one day. Constraint sets (4) and (5) ensure that if a piece is assigned to a batch l, this batch must be assigned to a furnace k and a day n. If no pieces are assigned to a batch, this batch must not be assigned to either a furnace or a day. Constraint sets (6) and (7) ensures that the day on which the piece is processed is the same assigned day to the batch that it belongs to. M is a constant that is big enough to activate binary variables in the constraints (4), (6), and (7). Constraint set (8) determines the delivery day of order j which is the day when the last piece that belongs to the order is processed. Constraint set (9) determines the tardiness of order j based on its delivery day and due date. Constraint sets (10) and (11) ensure that if pieces i and r are assigned to the same batch Zi,r = 1, otherwise Zi,r= 0. Constraint set (12) ensures that the pieces of a batch must have the same class. Constraint sets (13) and (14) ensure that the maximum ballistic level difference between the pieces of a batch cannot be greater than 1. Constraint set (15) ensures that the batch width must be less or equal to the assigned furnace width. Constraint sets (16) determines the processing time of the batch l:PTl,k,n. Which is the processing time of the piece of the batch that requires the longest time to process. Note that the variable PTl,k,n depends on n index because each furnace has different capacity times per day. If the batch l is assigned to a furnace k and a day n, PTl,k,n > 0. If it is not, PTl,k,n = 0. Constraint set (17) ensures that furnaces capacities are respected. Constraint set (18) determines the furnace use adding up all processing times of all the batches. Finally, the set of constraints from (19) to (26) specify the nature of the decision variables.
This formulation leads to a very large model with more than 450,000 variable and 100 million constraints (considering our case of 591 pieces, 152 orders, 4 furnaces, 160 batches in average, 7 ballistic levels, and 7 days). Even if we had reduced the size of the problem to only consider 100 pieces, 25 orders and batches, a planning horizon of just one day, and only one furnace, we would still end up with 12,000 variable and over 1 million constraints. Hence, exact methods are not an option to resolve the problem and heuristic approaches must be considered instead.
Methods
We developed two methods. The first one was based on dispatch rules, which find a feasible solution and improve current AGP results. The second method was a metaheuristic one that improved the distribution of pieces in the batches and found a better objective function.
Method No.1: Dispatch Algorithm
The first method consists of a fast heuristic based on dispatch rules to provide an initial solution to the Tabu Search algorithm.
The first heuristic is based on three criteria
-
A criterion to sort the pieces before creating the batches (PIA).
-
A criterion to check the possibility of assigning pieces to a batch (AC).
-
A criterion to sort the furnaces in order to assign the batches (FIA).
Figures 2 and 3 show the pseudocode and flow diagram of the heuristic.
First, the pieces are sorted according to a criterion that we called PIA (Piece Information Arrangement which is actually an LPT [longest processing time] dispatching rule). In our implementation we used decreasing processing times for this criterion (as we will describe later, we also tested other criteria such as due date or width but with worse results). Once pieces are sorted according to the PIA criterion, batches are created and assigned to a furnace (the furnace to which the batch is assigned later is determined by the criterion FIA). The first piece is assigned to a newly created batch. The following pieces are added to this batch as long as the AC (Allocation Criterion) is met. AC criterion basically makes sure that pieces within a batch are all compatible and that the batch can be processed in the furnace. When no additional piece can be added to the current batch, a new batch is created, and the same process is carried on again.
The batches are assigned to the furnaces according to the third criterion FIA (Furnace Information Arrangement). It reflects the fact that furnaces have different processing times and different capacities. This criterion sets a priority to the fastest furnaces on average (based on the company estimation) and with the highest capacity.
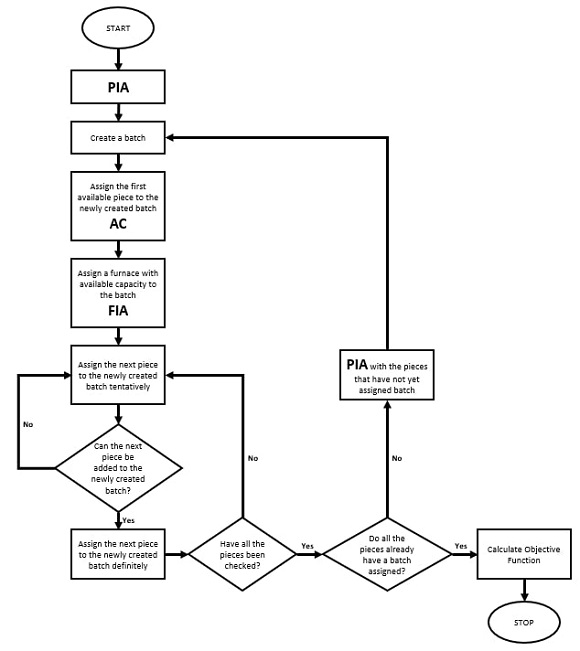 Figure 2.
Flow diagram of the heuristic
Figure 2.
Flow diagram of the heuristic
Source: Own elaboration
 Figure 3.
Pseudocode of the heuristic
Figure 3.
Pseudocode of the heuristic
Source: Own elaboration
Algorithm 1 shows a pseudo-code of the assignment algorithm. Line 2 organizes the pieces according to PIA and the furnaces according to FIA. Line 3 and 4 define two loops. The first one goes through the batches and the other one through the pieces. Lines 5 through 14 verify if batch l was not assigned to a furnace yet. If batch l is not assigned, line 6 verifies if piece i was not assigned to any batch, and if it is not, it is assigned to batch l (line 7). The subroutine is called in line 8. It will be explained below. If batch l was already assigned (line 10) then it is necessary to check if piece i could be assigned, according to all the explained constraints above, to batch l (lines 11 and 12).
The assignment of a batch is described in lines 19 through 29. The input parameter is batch l. Line 20 and 21 define two loops for the number_furnaces and number_days iterations, respectively. The first one goes through the furnaces and the other one through the production planning horizon. Line 22 verifies if batch l could be assigned to furnace k. This depends on the parameter (fik) of the piece that has already been assigned to batch l. Line 23 verifies if furnace k on day n has enough capacity to process the entire batch l. If it is possible, line 24 assigns batch l to furnace k on day n.
For a better understanding, an example is given with numerical parameters based on the one described in figure 1. Table 1 shows the sets that were defined in the mathematical model, tables 2 and 3 show the parameters of the pieces and furnaces, respectively. These data have been modified and do not correspond to the real data of AGP.
Table 1.
Sets Initialization
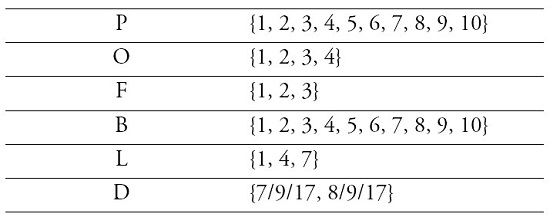
Source: Own elaboration
Table 2.
Piece parameters
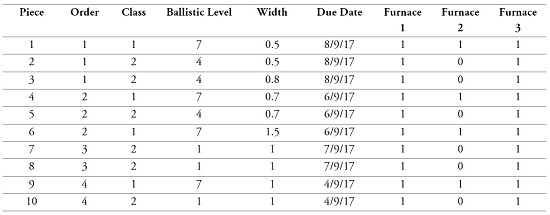
Source: Own elaboration
Table 3.
(a), (b), (c): Furnace parameters
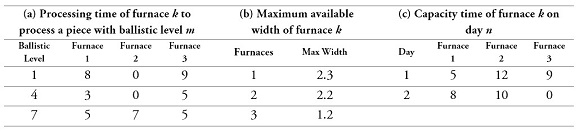
Source: Own elaboration
First (line 2) the algorithm organizes the pieces taking into account PIA criterion. In this case, all the pieces were organized in descending order according to piece processing time (which is also proportional to the ballistic level). The obtained arrangement was {1, 4, 6, 9, 5, 3, 2, 8, 7, 10}. Line 3 organizes the furnaces according to FIA criterion. In this example, all the furnaces were organized by the capacity of each one. The obtained arrangement was {2, 1, 3}.
In the first iteration, the piece that could be assigned to batch 1 was piece 1. As this piece could be processed in any furnace and there was still capacity available in all of them, batch 1 had to be assigned to furnace 2 on day 1, according to FIA. The next iteration showed that piece 4 could be assigned to batch 1 because it fulfilled all constraints (width, ballistic level, and class). On the other hand, the next piece, number 6, could not be assigned to this batch because the sum of all the widths of pieces 1, 4, and 6, was higher than the maximum width in furnace 2. Checking the rest of the pieces, piece 9 was the last one that could be added to batch 1.
In the second iteration of the l index loop the first piece available to be assigned to batch 2 was piece 6. Even though there was enough space to add other pieces, none of the other pieces (number 2, 3, 5, 7, 8, 10) fulfilled the assignment constraints. As this piece 6 could be processed in any furnace and there was still capacity available in the furnaces, batch 2 had to be assigned to the furnace 2 on day 2, because there was not enough capacity on day 1 to process the batch. If furnace 2 had not had sufficient capacity to process, the batch would have been assigned to furnace 1 (furnace 1 is the second-best choice according to the explained organization above). The same logic is applied until all pieces are assigned.
Table 4 shows the results of this example.
Table 4.
Results example
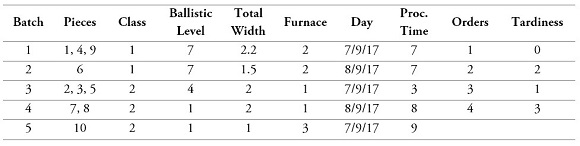
Source: Own elaboration
In this example the objective function is 1706. Tardiness of orders corresponds to 6 and usage hours of the furnaces corresponds to 34. In this case we are assuming the same values of the constants Wfurnaces and Wtardiness explained above.
Method No. 2: Tabu Search
Tabu Search is a metaheuristic that guides a local heuristic search procedure to explore the solution space beyond local optimality [7].
Our method is a mix between a classical Tabu Search and our heuristic algorithm presented above. In each iteration, Tabu decides the order of pieces that is then used as an input to Method 1 (it overrides the order given by the PIA criterion). For each order given by Tabu, Method 1 recreates the new batches, assigns the furnaces, and calculates the new objective function (figure 4).
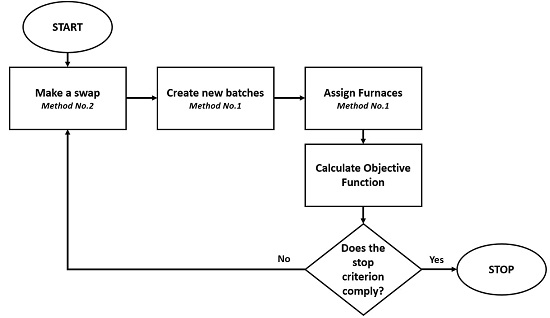 Figure 4.
Hybridization between method no. 1 and method no. 2
Figure 4.
Hybridization between method no. 1 and method no. 2
Source: Own elaboration
The neighborhood explored in each iteration consists in all the swaps that can be done between two pieces as shown in figure 5.
 Figure 5.
Change the arrangement of the piece, method no. 2
Figure 5.
Change the arrangement of the piece, method no. 2
Source: Own elaboration
No aspiration criterion was used in the Tabu. For the stopping criterion we chose the number of iterations without improving the objective function. We performed several tests and beyond 10 iterations the algorithm did not improve any further. We also adjusted the size of the Tabu list to 50 by performing several tests. The computational time depends on the number of pieces we consider, 1 minute for 99 pieces and 7 minutes for 201 pieces.
Numerical Results
To solve the problem, we developed a software that processes the initial data of the problem and finds the programming of the production in a planning horizon of 1 week in AGP.
Before comparing our results to the AGP solution, we ran some instances of our metaheuristic and compared them to the exact mathematical model presented above.
We ran 12 random instances. We had to select small instances for which CPLEX could find an optimal solution in less than an hour. We decided to set this limit as the objective set by the company is to be able to find a good solution in a less than a few minutes.
Table 5.
Mathematical model and Tabu search results
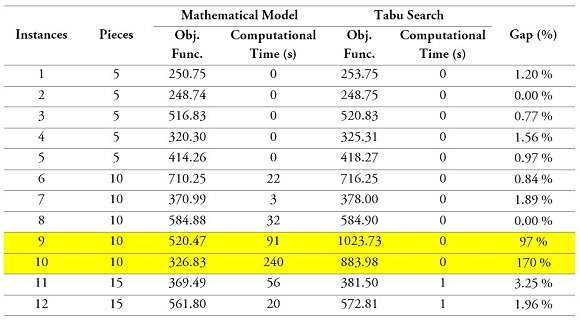
Source: Own elaboration
We can observe in table 5 that in all instances our heuristic runs in less than 1 second. In most cases our gap compared to the optimal solution is less than 5 %. We notice however that in two cases we have solutions that are pretty far from the optimum. Keep in mind that our objective was to find a solution that is good enough to improve the current solution of the company in a very short time. That is why we will focus the rest of the analysis on the company’s case study. However, we leave for further studies the research on the specific characteristics of the instances that make our algorithm unstable.
In the following section we present first the results obtained from the case study. This instance has 152 orders that represent 591 pieces. The number of furnaces considered for this case were 4. Once the application is executed according to the input parameters established for this case, we proceeded to analyze the results obtained from the designed methods. We compared our results with the current results of the plant in the selected week that was used as case study.
Case Study
A significant improvement in the objective function was achieved of 31.65 %, represented mostly by a reduction of 32.03 % in hours of furnace use. This is a valuable result for the company as it means they can fulfill the same demand with less resources. We also reduced by 7.42 % the tardiness delivery of orders.
We also analyzed the performance of the algorithm developed in order to illustrate how the Tabu Search improves the objective function obtained by the first method. In this instance, we considered the same 4 furnaces and the same input parameters, but we changed the number of orders to analyze the behavior of the algorithm as the size of the problem changes. We can see that for small instances the Tabu does not improve the objective function in a significant way. For larger instances, the Tabu search improves the initial solution in a range between 5 and 10 % (figure 6)
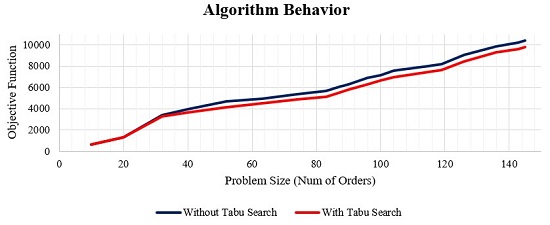 Figure 6.
Behavior of the developed algorithm with and without Tabu Search
Figure 6.
Behavior of the developed algorithm with and without Tabu Search
Source: Own elaboration
Finally, we performed statistical tests to evaluate the sensitivity to the PIA criteria of both of our methods. We considered sorting the pieces according to an ascending and descending order of the processing time (which is determined by the pieces’ ballistic level), width, and delivery dates. Therefore, we can list six different criteria for PIA which could lead to different initial solution values. These statistical tests were build considering samples of ten instances for two scenarios that varied depending on the number of pieces. In the first scenario, each sample is related to an instance with 201 pieces, randomly selected from the 591 pieces available from the information given by AGP. In the second scenario, each sample is related to an instance with 99 pieces, also randomly selected. We then analyzed the difference of the mean objective function obtained with the “descending processing time” rule (which was the one we used in this research as it gave better results) and each one of the 5 remaining ordering criteria. A paired t-test was performed considering a 95 % significance level. The null hypothesis is defined as “the means of the two objective functions are equal.”
In the case with 201 pieces, the results show that the null hypothesis is rejected for both the heuristic and Tabu search. This means that both methods are sensitive to the PIA criteria.
However, in the case of 99 pieces, the null hypothesis is always accepted for the Tabu, while for the Heuristic, it is only accepted in one comparison and rejected for the 4 remaining ones. This suggests that with smaller problems, Tabu is robust enough to reach the same objective function regardless of the value of the initial solution. Table 6 shows the results.
Table 6.
Results example
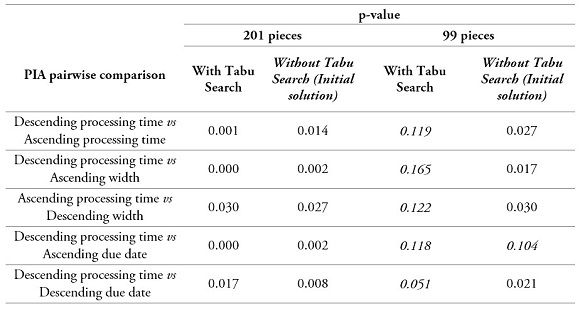
Source: Own elaboration
Conclusions
This paper considered a real-world scheduling problem commonly observed in AGP. As the problem under study was NP-hard, a hybridization of two methods was developed. The algorithm’s results were compared with AGP’s previous solution. We showed that optimization techniques can improve the overall production process reducing the objective function by 30 %. Being able to reduce furnace capacity not only means that more orders can be processed in less time, but it also helps AGP to rethink its established procedures.
This project will serve AGP as a first step to define new criteria for the operation in the bending process. A good process optimization allows companies to offer a higher quality service and customer satisfaction, which is a fundamental factor for organizations.







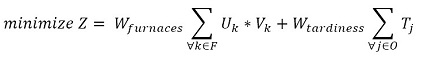 (1)
(1)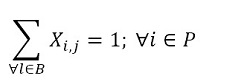 (2)
(2)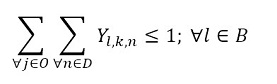 (3)
(3)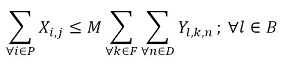 (4)
(4)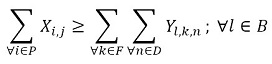 (5)
(5)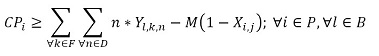 (6)
(6)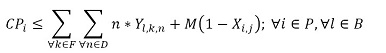 (7)
(7)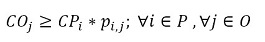 (8)
(8)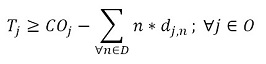 (9)
(9)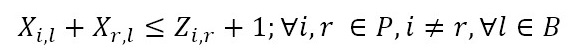 (10)
(10)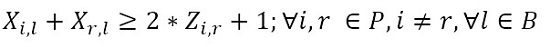 (11)
(11)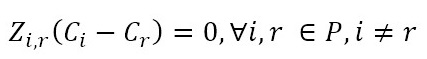 (12)
(12)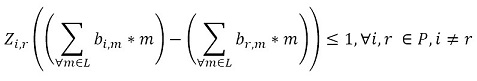 (13)
(13)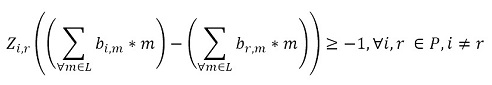 (14)
(14)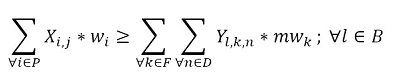 (15)
(15)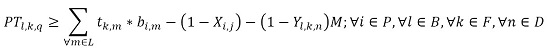 (16)
(16)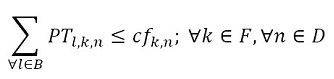 (17)
(17)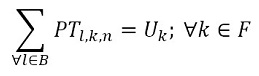 (18)
(18)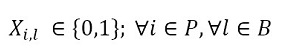 (19)
(19)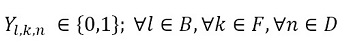 (20)
(20)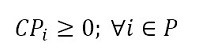 (21)
(21)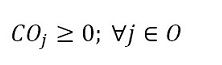 (22)
(22)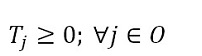 (23)
(23)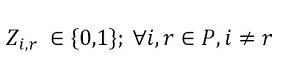 (24)
(24)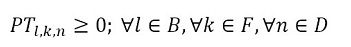 (25)
(25)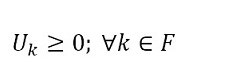 (26)
(26)










