Motion intent detection is a process focused on determining a user’s voluntary command, primarily for the control of external systems. Said detection could be achieved based on bioelectric signals such as the signals captured through electromyography (EMG). EMG analysis can be used in applications such as the diagnosis and analysis of anomalies related to alterations in the way movement is made, which allows for the detection of the presence of pathologies, and also in applications for the control of robots and exoskeletons [1].
In this way, EMG signal processing is a useful tool for the detection of movement intent through the recording of action potentials produced by the activation of skeletal muscles, where the EMG signal is made up of consecutive discharges known as motor unit action potentials (MUAPs) [2], [3]. The EMG signal is the result of the sum of overlapping MUAPs; therefore, it can be broken down into the activity of each of them [4]. A non-invasive technique in which electrodes are placed on the surface of the skin, known as surface electromyography (sEMG), is preferred to record this type of signals [3]. sEMG is a safe technique, given that it does not require the electrode to be inserted into the skin and muscle and it provides information on the electrical activity of the muscle; however, the sEMG signal can record information from multiple muscles, show interferences from other biopotentials (ECG, EOG, etc.), among other drawbacks [1]. sEMG signals have different applications such as ergonomic assessment, neuromuscular diagnosis, commands for the control of prosthetic and assistive devices that have human-machine interaction (HMI), and indication of muscle fatigue [5], [6].
Pattern recognition-based myoelectric control has emerged as a promising alternative in rehabilitation systems. These systems support their classification theory on the extraction of information on the possible movement intent from the acquisition of surface myoelectric signals. The performance efficiency of the pattern recognition and classification algorithms lies in the implementation of three modules, which consist of pre-processing, feature extraction, and pattern classification.
The feature extraction stage is important for classification systems because raw sEMG signals cannot be used directly in applications such as, for example, machine control [7]. Some of these feature extraction techniques include the representation of sEMG signals as frequency through the Discrete Fourier Transform (TDF) or as time-frequency through the Discrete Wavelet Transform (DWT) [8]. The sEMG signal analysis can also be performed in the time domain, using the root mean square (RMS) value, zero crossings (ZC), and the normalized energy of the signal in a specific time interval [9]. The ZC technique that counts the time in which the signal changes sign is among the most widely used and has been used as a feature of pattern recognition algorithms used for assistive device movement control techniques [9], [10]. The autoregressive (AR) prediction model, which describes each sample of the EMG signal as a linear combination of the previous samples, has been used as a tool to improve the performance of the pattern recognition algorithm based on myoelectric control [11]. It is relevant for DWT because it removes unwanted interferences and provides information simultaneously in the time and frequency domains [12], and has been used with good results to classify intramuscular sEMG signals to differentiate normal signals in patients with amyotrophic lateral sclerosis or with myopathies. In this case, the coefficients generated by the DWT are characterized by statistical functions [8].
Despite the different strategies for feature extraction, the issue on which ones to use is a question that remains unanswered. Among the strategies to select the type of features to be used to represent the EMG signal against a classification system, we can find even the most basic steps, which include dismissing characteristics with large amounts of missing data, little variance in their distribution or eliminating those with high correlation values between two characteristics to avoid information redundancy. At the same time, the classification model has to be used to determine which features are the most appropriate for the purpose of the study [13], [14]. However, the selection may change depending on the classification system and the problem to be tackled [15], [16].
After performing feature extraction, signals are represented in a feature vector aiming for a classification stage [17], [18]. To perform this task, different applications use techniques such as linear discriminant analysis (LDA), logistic regression, k-nearest neighbors (k-NN), up to computationally demanding methods such as support vector machines (SVM) and artificial neural networks (ANN) [19]. Among the classification methods explored are ANNs, which are mathematical models inspired by the functional aspects of brain structures [20] and allow for their implementation in hardware and embedded platforms for their simple structure [20].
Research on EMG signal processing techniques–on the detection of movement intent for its different application areas, which include rehabilitation, myoelectric control, and diagnosis–show that some studies aimed at the detection of hand movement focus on pronation, supination, flexion and extension movements [9], [10], [11], [12]. Few works have been implemented on the range of motion of the wrist joint. This approach could be a useful tool that provides information on specific movements as given by the different angles in the range of motion of the wrist when performing the flexion-extension movement. The information on the estimation of the articular range of motion of the wrist from sEMG can be used to implement proportional myoelectric control schemes in applications ranging from assistance to motor rehabilitation [21], [22].
This work presents the results obtained in a comparative study on the use of different groups of features based on the domain they were obtained: time, frequency, and time-frequency. In this way, it was determined which one of them works best to identify the flexion-extension angle using machine learning tools. For said tools, multilayer perceptron artificial neural networks were used, as well as vector support machines, which were all focused on the classification of 5 angular positions at the wrist level, given that they are two of the most widely used techniques for this type of task.
Methodology
The methodology used is based on the analysis of the signals obtained for the study and the classification made to obtain the angular positions of the wrist. Figure 1 shows the block diagram of the methodology. Three important processes are carried out: preprocessing, feature extraction and a final classification stage based on machine learning techniques.
Equipment and Materials
The protocol requires the acquisition of sEMG signals and of the joint range of motion for the flexion-extension movement of the wrist. Signal acquisition is performed using ADInstruments’ 8-channel Powerlab 8/30 biosignal acquisition system and the Labchart acquisition software. In addition, the SG65 electrogoniometer from Biometrics, which provides an analog signal proportional to the joint range of motion, was used to obtain the joint range of motion information. Taking into account that the frequency range of the sEMG signal is between 20 Hz and 500 Hz [23], the sampling frequency of the signals was 2 kHz. The sEMG signals are filtered within the band of interest in Labchart (bandpass filter between 20 Hz and 500 Hz).
Database
The database was built with the sEMG signals taken from a selected group of ten healthy people, aged between 20 and 25 years, who voluntarily participated in the data collection. The acquisition was performed following the SENIAM guidelines [24], with a bipolar placement of the electrodes on the right forearm, on the muscles involved in the flexion-extension movement of the hand (figure 2). Each subject performed two repetitions, completing a total of 20 acquisitions. During each repetition, the subject held an angular position of the wrist joint. Five different positions were performed from maximum flexion (85°) to maximum extension (-70°), covering the entire range of motion of the wrist joint (figure 3). During acquisition, a total of six channels were recorded for each subject, the first corresponding to an electrogoniometer, which produced a voltage output at a specific angle, and the remaining five electrodes corresponding to information from the sEMG.
Preprocessing
The signals acquired with a 500 Hz bandwidth underwent a preprocessing stage before the feature extraction. Filters additional to those implemented in the acquisition equipment were not used to take better advantage of the bandwidth in the search for features in the obtained frequency range.
First, signal normalization was performed to correct variations in signal amplitude for the different tests performed by each patient [25]. The procedure for this standardization was developed based on the scale. Equation (1) shows how normalization was calculated, making the signals range from -1 to 1:
where xN is the normalized version of x, from its minimum xmin and maximum xmax, ensuring that the normalized signal is within the interval [-1,1].
After normalization, segmentation was performed, a vital process for a pattern recognition system in which the sEMG signal is taken and divided into time windows from which the features will be extracted. In this way, the signal must be divided into segments with a length of 200 ms to 300 ms, which allows for movements to be identified and relevant features to be extracted [26], [27]. For this study, this segmentation was performed at 250 ms, with 500 samples per window and with a 50 % overlap.
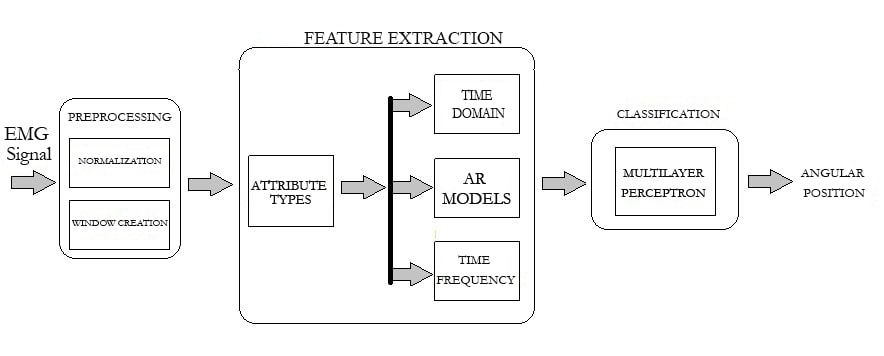 Figure 1.
Block diagram of the methodology used
Figure 1.
Block diagram of the methodology used
Source: Own elaboration
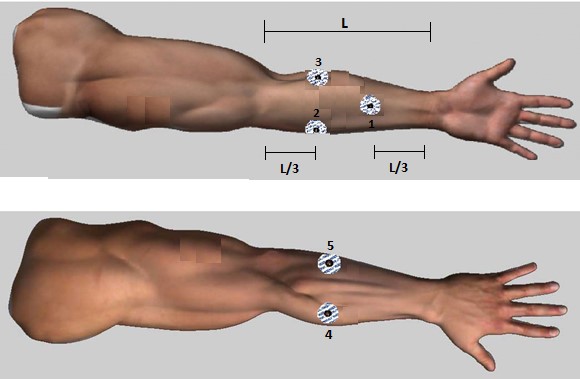 Figure 2.
Electrode placement for the acquisition of EMG signals
Figure 2.
Electrode placement for the acquisition of EMG signals
Source: Own elaboration
Feature Extraction
As mentioned, the purpose of this work is to compare three different groups of features in the process of classifying wrist flexion-extension angles. To accomplish this, features extracted in the time domain are analyzed first, then features obtained through an autoregressive model, and finally, features in the time-frequency domain.
Time Domain Features
Features in the time domain are the most frequently used for myoelectric classification, given that they do not need a transformation because they are based on the amplitude of the signal [28]. This type of features is widely used because they are simple to obtain and have a low computational cost [15], [22], [29]. To this effect, the features used in this work were: i) the root mean square (RMS) value, calculated through expression (2), ii) the mean absolute value (MAV), obtained through (3), iii) the number of zero crossings, which was calculated by means of (4), iv) the integral of the signal through the calculation of (5), and v) the signal power, which is obtained through the use of (6).
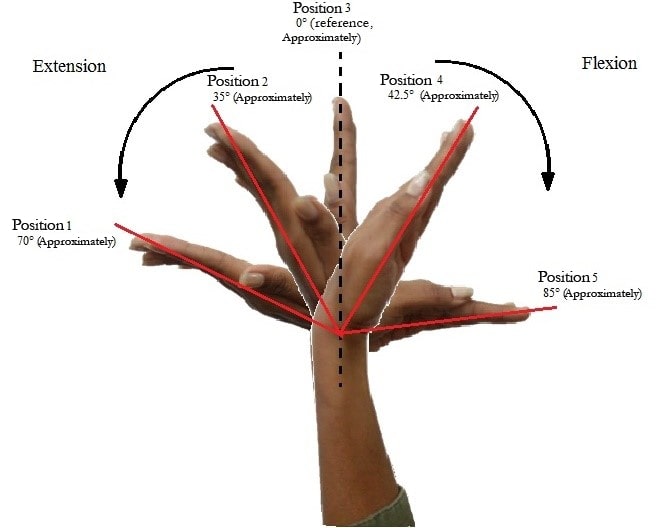 Figure 3.
Angular positions of the wrist joint performed
Figure 3.
Angular positions of the wrist joint performed
Source: Own elaboration
Root mean square:
Multiple studies in literature have mathematically modeled the EMG signal as a random process [30]. The RMS value provides the best probability of estimating the EMG amplitude during muscle contractions under conditions of constant force and fatigue-free contraction [30]. Its value is used to quantify the electrical signal since it is the reflection of the physiological activity in the motor units
where M is the number of samples of signal x and xm
is the value of signal x at time instant m.
Mean absolute value:
It is estimated from the sum of the absolute values and the measurement of the contraction levels of the sEMG signal, representing the contractile force of the muscle [31].
as in expression (2), M is the number of samples of signal x and xm
is the value of signal x at time instant m and the operator |.| represents absolute value.
Zero crossings (ZC):
Zero crossings count the number of times the signal passes through the zero line, that is, how many times has it gone from a negative value to a positive value and vice versa. The threshold is added to reduce the effect of noise [32].
xm is the value of signal x at time instant m.
Integral of the signal (IEMG):
It is the sum of the absolute value of the sEMG signal amplitude. It is normally used to indicate the onset of muscle contraction in clinical applications. It is related to the trigger point of the signal sequence [33]
as in previous expressions, M is the number of samples of signal x and xm is the value of signal x at time instant m.
Signal power:
This value is obtained by adding the power of the interval of the signal under study [30], using the expression:
where M is the number of samples of signal x and xm
is the value of signal x at time instant m.
After extracting this group of features, each signal window is represented by a five-value vector given by the features described above. Since each angular position was measured simultaneously by five electrodes, each one of these positions will then be represented by a vector of 25 features for this particular group.
Features Extracted from the Parameters of an Autoregressive Model
The modeling of a time series can be determined through parameters that represent said signal. Thus, it has been reported in literature that the amplitude of an EMG signal is stochastic in nature and can be represented by an autoregressive (AR) model. AR models are widely used in pattern recognition from sEMG signals [15], [29]. In this type of model, the coefficients are used as a prediction model that describe each sample xi of the sEMG signal as a linear combination of previous samples plus a residual wi [34] and is represented by:
where 𝑎k is the k-th coefficient of the AR model, n is the order of the model, and w is Gaussian residual noise. A sixth order model was used for this work because previous studies have shown that this type of model is best suited for the representation of sEMG signals [34] and [35]. The Levinson-Durbin recursion was used to calculate the coefficients using the autocorrelation sequence according to [36]. Upon completion, a vector of seven values is obtained, which represents the signal window. This process was performed for each electrode used in the acquisition.
Time Frequency Domain Features
In order to use the signal representation in terms of both time and frequency, this type of technique has been used in recent decades since Englehart’s work [37]. One of the most widely used forms is DWT, where the signal is broken down through filters and analyzed in different frequency bands with different resolutions that provide approximation and detail information in the time and frequency domains simultaneously.
The calculation of the discrete wavelet transform is an implementation of the wavelet transform using a discrete set for scales and translations, obeying defined rules, and decomposing a signal x[n] into a set of mutually orthogonal wavelets. The calculation process to obtain the decomposition of a signal x[n] through the DWT is analogous to the use of a filter bank [38] (see figure 4); for this purpose, we can represent this decomposition as:
where uk[u] is each of the decompositions of input signal x[n], h1,1[n] is the scaled and displaced mother wavelet, and L is the number of decomposition levels. In this case, the signals used as bank input were each of the windows previously described in the preprocessing subsection. The structure of the filter bank is comprised by a dyadic tree with two filters, a low-pass one and a high-pass one, and a subsampling by two in each branch, according to the number of filters used. For this case, three levels and a daubechies4 mother wavelet were used, based on the values and parameters recorded in the literature [28], [36], [39]. Likewise, as reported in these works, the mean, standard deviation, and power values were calculated and used as features for each level obtained. There is a vector of 12 features for each electrode used in the acquisition for this group of features.
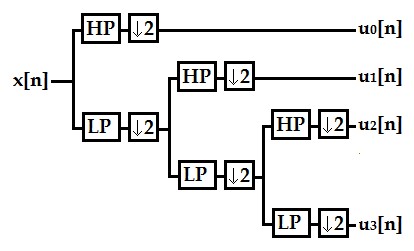 Figure 4.
Filter banks to attain signal decomposition using a three-level DWT. HP: High pass, LP: Low pass
Figure 4.
Filter banks to attain signal decomposition using a three-level DWT. HP: High pass, LP: Low pass
Source: Own elaboration
Classification
This stage of the methodology describes the models used to classify the five classes represented by each of the proposed angles. As such, it is necessary to describe first some details of the data used for model training. Table 1 summarizes the number of features for each group used, showing the size of each entry for every case. Another important factor is the number of instances or patterns, given the process to obtain features. This number is given for each of the windows obtained, for each of the repetitions per person (20 in total); for each one of the angular positions, approximately 80 windows were obtained from which the features were extracted. In other words, there are a total of 1600 instances per position, which is an approximation because each subject did not hold the exact position in terms of milliseconds during the acquisition process.
Table 1.
Total number of parameters for each group of features
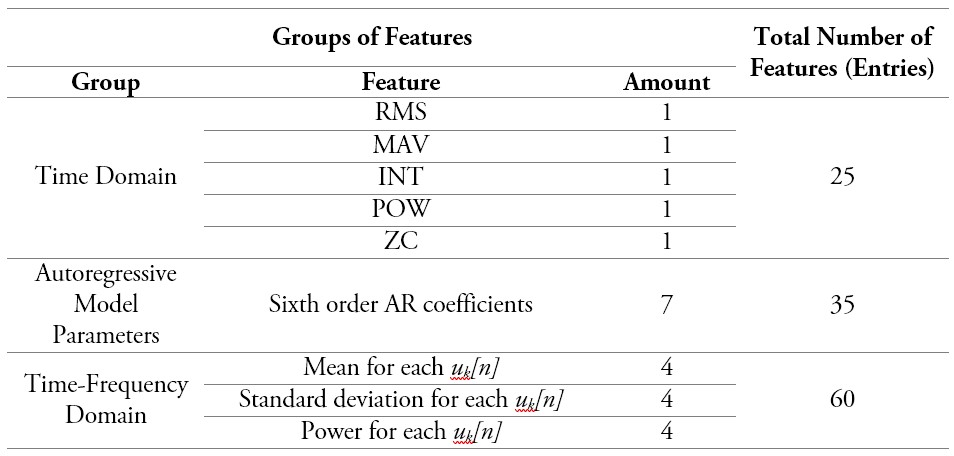
Source: Own elaboration
The cross-validation method was used for model training using four groups (k-folds) for this purpose [40], [41]. In this way, each group was the result of combining the features of five subjects for the five wrist positions, resulting in a total of 6000 instances for training and 2000 instances for model validation. Also, trainings were implemented with each group of features as well as with combinations of the groups to observe the differences, obtaining a total of seven classification scenarios.
The measures used to compare the groups of features and the models used for the classification were based on the classification rate given that there are five classes: 70°, 35°, 0°, -43°, -85 ° (figure 3). All computational experiments were performed in the Matlab© software through its digital signal processing and machine learning toolboxes.
Artificial Neural Networks
There are different artificial neural network models according to their architecture and training mode. For this work, multilayer perceptron (MLP) was chosen to perform the classification task due to its capabilities to establish relationships between input-output vectors in a supervised learning procedure, which in turn is due to its ability to learn complex nonlinear patterns by adjusting its synaptic weights that link artificial neurons with nonlinear activation functions [41].
MLP models have shown good results in the classification of sEMG signals, which is why they have been chosen to perform the task of position differentiation [19], [42]. In this work, a two-layer architecture was chosen: a hidden one and an output one. The number of inputs is established by the group of features to be used in training (table 1); the number of neurons in the hidden layer was found through experimentation, varying from one to ten neurons, and the number of neurons in the output is determined by the five angular positions of the wrist. Figure 5 shows the model used for classification, where all connections between neurons are forward connections. The activation functions of neurons were hyperbolic tangent in the hidden layer and a softmax function in the output layer.
The training algorithm is resilient backpropagation [43], which shows a higher speed due to its modification based on the sign of the gradient. The maximum number of training epochs was set to 800, with a root mean square error as a cost function because its convergence was found through experimentation. Among the training stoppage criteria, the maximum number of epochs, a training error of zero, and premature stoppage were considered, with an observation window of 250 iterations.
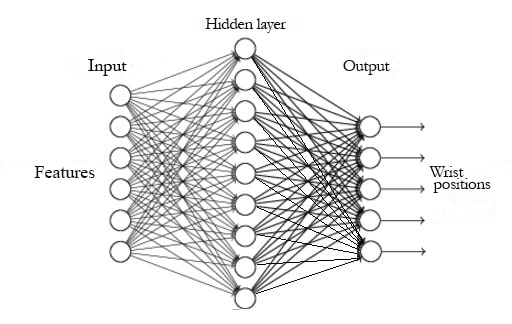 Figure 5.
Neural network model used for classification
Figure 5.
Neural network model used for classification
Source: Own elaboration
Support Vector Machines
This machine learning technique, used for pattern recognition and classification, is a development of statistical learning theory [44]. Vector support machines, as it was mentioned in the introduction, have been used to work in conjunction with sEMG signals. Their main function is in the differentiation stage, mainly in the detection of neuromuscular pathologies [19], [36], [45], [46], [47], [48]. In this case, the parameter adjustment of the SVM models was performed in a similar way as done with neural networks. Four folds as those described above were also used, again performing cross-validation between the different features and five classes. Taking into account that this technique, by nature, has a binary classification [36], it was necessary to establish a multiclass SVM, which would evaluate one class against all the others.
Initially, SVM models were developed for a classification given by a linear function [44], [48], and it is for this reason that it is necessary to perform a non-linear transformation through a kernel function. So, said transformation allows the SVM to perform a linear classification of a data set that originally did not have this characteristic. The kernel function projects data from a low dimension space to a larger dimension space, and it is in said new space that the initial formulation of the model is used with a linear two-class classification [49]. For this work, the following kernel functions were used: radial base function (RBF), polynomial, and quadratic, given that the basic linear function of the SVM yielded poor results. All these non-linear kernels allow for faster training, which facilitates the convergence of the algorithm, and also for the obtainment of a similarity between input vectors and their combinations and the suppression of as many support vector multipliers as possible, thus minimizing the number of support vectors required for classification.
Results
The three groups of characteristics, as well as combinations between them, were used in the classification using the MLP and SVM models. Table 2 summarizes all the results in terms of classification rates for each of the characteristic groups used, as well as for the combinations implemented. In the case of neural network classification, the best result of each of the four validations was used to calculate the mean and standard deviation shown in the table. Also, the maximum number of neurons in the hidden layer (N) is recorded to determine the size of the model. Also reported for the SVM classification, are the average values of the cross-validation of four groups and the type of kernel with which the results were obtained.
Given that, in the case of the MLP models, experiments were performed one hundred times to evaluate the behavior against the initialization of the synaptic weights, figure 6 shows box plots for those one hundred results with the different architectures (two to ten neurons) for the best of the four validations used, using the features in the time domain as input. Likewise, figure 7 shows the best results obtained when the combination of the groups of features given by the AR model and the time-frequency domain is used.
It is possible to see that the best results were obtained by combining the features extracted through the AR models and the time-frequency domain (DWT), where a classification rate of 81.8 % and 58.3 % was obtained for the MLP and SVM models, respectively. The worst group of features was the one obtained through analysis measures in the time domain, with only a 53.1 % and 22.5 %, respectively (table 2).
In the MLP models, experiments with other training parameters such as hyperbolic tangent activation functions in the neurons of the output layer, variation in the number of epochs and other cost functions were implemented, obtaining results with lower classification rates when compared to the values shown in table 2. In the case of SVM models, the parameter initialization problem is not present, since the support vectors are found in the training set, therefore, results will not change. Other models with a different kernel were tested without any improvement in the results obtained.
Table 2.
Results of the classification
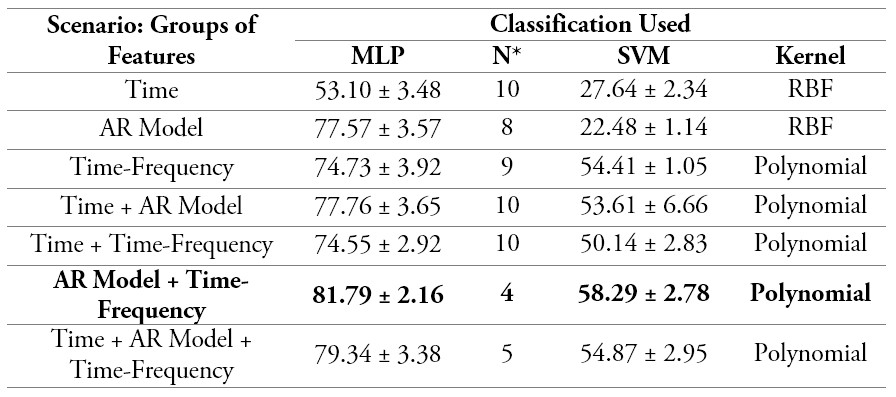
N*Neurons in the hidden layer
Source: Own elaboration
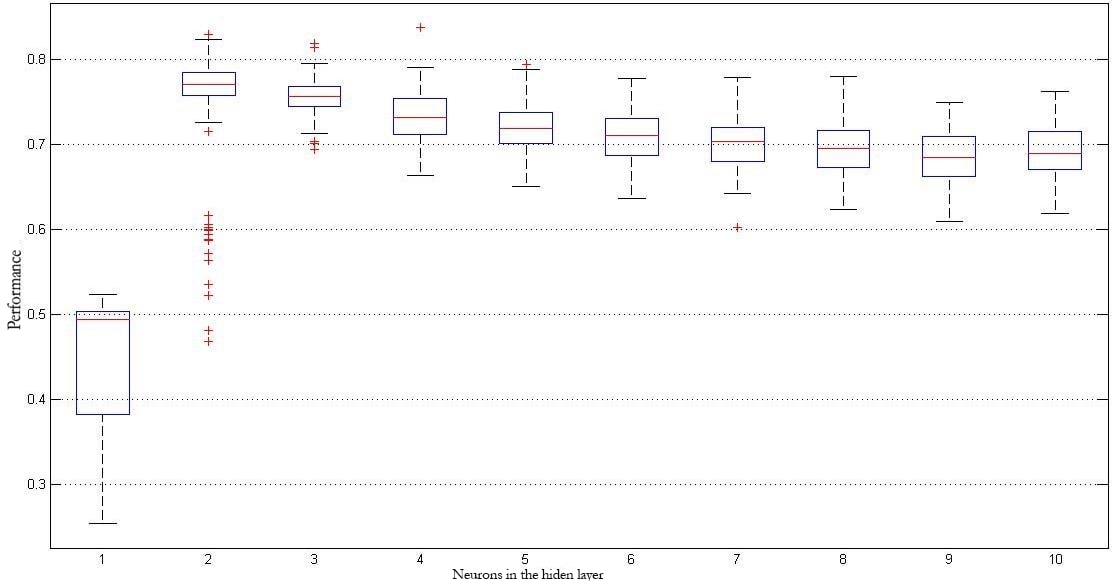 Figure 6.
Best classification results using only time-domain characteristics.
Figure 6.
Best classification results using only time-domain characteristics.
Source: Own elaboration
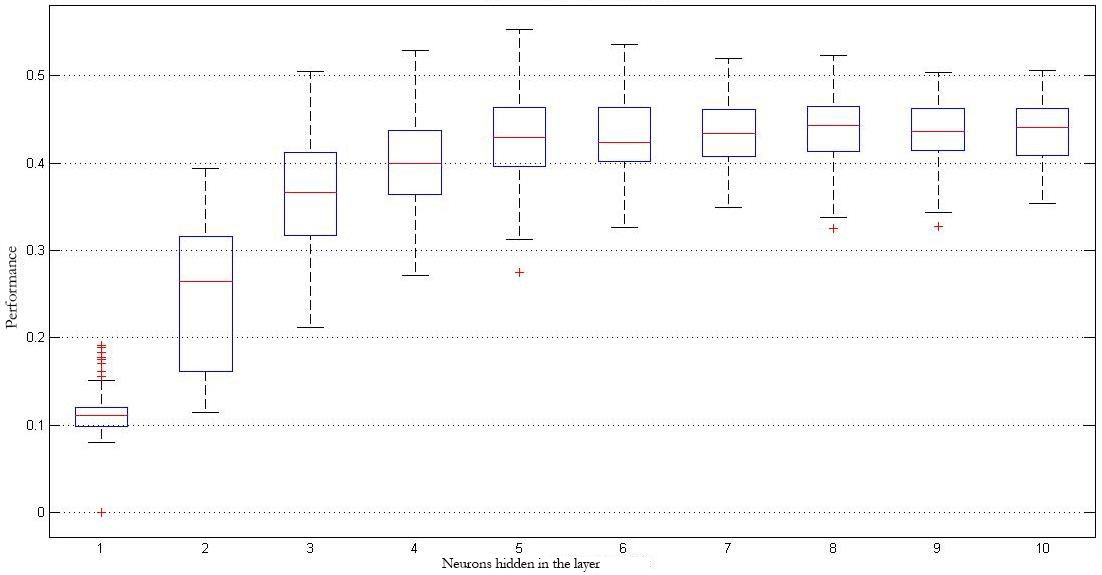 Figure 7.
Best classification results using characteristics extracted from the AR Model + Time-Frequency Domain.
Figure 7.
Best classification results using characteristics extracted from the AR Model + Time-Frequency Domain.
Source: Own elaboration
Discussion
Based on the classification results obtained from the use of the different groups of features, it is inferred that the features based on the coefficients of the AR model are the most appropriate as input for the classifier for this application, with a rate of 77.57 % for the MLP network and 53.6 % for the SVM. These results are closely followed with 74.73 % for the classifier with MLP and improving to 54.4 % for the SVM based on the features obtained with the analysis in the time-frequency domain offered by the DWT. Regarding the general results for the SVM model, previous classification results for the detection of neuromuscular pathologies had a sensitivity of 55.6 % for binary classifiers in [50]; this is a consequence of using this type of classifier in multiclass problems, where the complexity of the classifier function is more demanding given that, for the classes considered in this work, it is not possible to assume distributions that represent said data [51].
Based on the classification results obtained when groups of features are combined, the first place is held by the combination of the groups given by AR models and the Time-Frequency domain. For this case, the classification rates obtained for the classifiers implemented with MLP and SVM were 81.79 % and 58.3 %, respectively. These results are followed for the case when all features were implemented, where the classification rate values were 79.34 % and 54.9 %. So, based on this information it is possible to conclude that the features in the time domain do not contribute much information to the classification implemented. The reason behind this is that there is no significant difference between the use or lack thereof of these characteristics when used simultaneously with other groups.
The results obtained in this article are consistent with the reports of previous studies. The works in [21], [52] used neural networks to determine the joint range of motion of the degrees of freedom of the wrist in a continuous angle prediction. Considering the flexion-extension of the wrist, in [21] results of 72.0 % ± 8.29 % in healthy subjects were reported and in [52] an R2 between 0.81 and 0.94 was reported. A greater number of EMG channels were used in said studies when compared to those used in this study, which is considered as a difference that did not allow for an equitable comparison. However, in the work of Jiang et al. in [21], results were reported in the range between 79 %-88 % in terms of accuracy for the same movement performed in this study. In the case of SVM, works such as that of Naik et al. [51], where they classified finger movements and wrist flexion, achieved classification rates of 87.7 % for seven different movements and specialized models known as Twin SVM, where the kernel was optimized for each problem or class. Shim and Lee in [53] used a three-layer Deep Belief Network (DBN) to differentiate five movements at the wrist level. In this case, the authors reported classification rates of 88.5 % for the DBN compared to 80.5 % when using SVM models with an RBF kernel. Similarly, it has been reported in the literature that creating feature vectors using a combination of features, preferably obtained by wavelet transforms, can prove helpful in a better classification of EMG signals [54].
A more in depth analysis of the results provided by the neural networks makes it possible to mention that the dispersion of the results obtained for the use of features in the Time domain compared to the results of the best combination (AR models plus Time-Frequency) is quite different. It can be seen that for the first case, results dispersion is greater, showing that the obtained classification model has a large fluctuation (figure 6). When features obtained from the AR-based models and Time-Frequency coefficients are combined, the dispersion is lower, showing more consistent models (figure 7). Also, it is possible to observe how as the number of neurons in the hidden layer of the MLP model is increased, results begin to decrease, with a peak when there are between two and three neurons. This shows that the classification model starts to be over trained, adjusting to the training data and offering low results in terms of generalization.
Regarding the limitations of this work, we note the number of participants from whom the signals were obtained, with the cooperation of ten subjects who duplicated the acquisition, for a final size of 20 repetitions. This number is lower when compared to other studies, where more users were enrolled, such as the use of signals from 28 participants in [54], or 27 subjects in [50], thereby considering this point as a strong disadvantage for this present study. Another factor that shows a certain limitation is the use of more elaborate models, given that modifications of the SVM model and deep neural networks have been previously worked on in [48] and [50]. However, the main objective of this work was to compare groups of features in terms of their domain and observe which ones behave better for the classification to determine angles at the wrist level. For this reason, this type of analysis is beyond our main objective, as well as the reduction in size of the features, since the objective was to study them as a group. These considerations can be accounted for in future works, where more modifications can be included.
Conclusions
In this study, classification models were used to analyze groups of features extracted from sEMG signals. The results showed that the use of features extracted from the signal in the time domain were the lowest to classify the angular positions of the wrist in flexion-extension movement. The results of this work establish that the use of features in the time-frequency domain offer a better alternative for future studies in which it is necessary to use the classification of the articular range of the wrist for applications that require accuracy.
In this way, the best classification results were obtained when groups of features from the coefficients of autoregressive models and characteristics in the time-frequency domain were used, attaining an 81.8 % in the classification of the five angular positions of the wrist.
Acknowledgments
The authors would like to thank the School of Medicine and Health Sciences of the Universidad del Rosario, as well as the Universidad Antonio Nariño for financing the development of this work, through the project identified with the code 2019213.
References
[1] R. Merletti and P. A. Parker, Electromyography: Physiology, Engineering, and Non-invasive Applications. Hoboken, NJ: John Wiley & Sons, 2004.
[2] C. Germany, “A low cost signal acquisition board design for myopathy’s EMG database construction,” in 13th Int. Multi-Conf. Syst. Signals Devices (SSD), 2016, pp. 274–279. doi: 10.1109/SSD.2016.7473767
[3] S. Kalwa, “Neuromuscular disease classification based on discrete wavelet transform of dominant motor unit action potential of EMG signal,” in 2015 Int. Conf. Inf. Process. (ICIP), 2015. doi: 10.1109/INFOP.2015.7489474
[4] A. A. Ali, A. Albarahany, and L. Quan, “EMG signals detection technique in voluntary muscle movement,” in 6th Int. Conf. New Trends Inf. Sci. Serv. Sci. Data Min. (ISSDM), Taipei, Taiwan, 2012, pp. 738–742. Available: https://ieeexplore.ieee.org/document/6528730
[5] S. Thongpanja, A. Phinyomark, F. Quaine, Y. Laurillau, C. Limsakul, and P. Phukpattaranont, “Probability density functions of stationary surface EMG signals in noisy environments,” IEEE Trans. Instrum. Meas., 2016, vol. 65, no. 7, pp. 1547–1557. Available: https://ieeexplore.ieee.org/document/7438830
[6] F. Ortes, D. Karabulut, and Y. Z. Arslan, “General perspectives on electromyography signal features and classifiers used for control of human arm prosthetics,” in Adv. Methodol. Technol. Eng. Environ. Sci. Hershey, PA: IGI Global, 2019, pp. 1–17. https://doi.org/10.4018/978-1-5225-7359-3.ch001
[7] C. Garg, “Development of a software module for feature extraction and classification of EMG signals,” in Conf. Commun. Control Intell. Syst. (CCIS), 2015, pp. 250–254.
[8] C. J. G. Duque, L. D. Muñoz, J. G. Mejía, and E. D. Trejos, “Discrete wavelet transform and k-nn classification in EMG signals for diagnosis of neuromuscular disorders,” in Image, Signal Process. Artificial Vision (STSIVA), 2014 XIX Sym., pp. 1–5. Available: https://ieeexplore.ieee.org/document/7010171
[9] M. Jahan, M. Manas, B. B. Sharma, and B. B. Gogoi, “Feature extraction and pattern recognition of EMG-based signal for hand movements,” in Adv. Comput. Commun. (ISACC), 2015 Int. Sym., pp. 49–52. Available: https://ieeexplore.ieee.org/document/7377314
[10] C. Sapsanis, G. Georgoulas, and A. Tzes, “EMG based classification of basic hand movements based on time-frequency features,” in Control Autom. (MED), 2013 21st Mediterranean Conf., pp. 716–722. Available: https://ieeexplore.ieee.org/document/6608802
[11] L. Pan, D. Zhang, X. Sheng, and X. Zhu, “Residuals of autoregressive model providing additional information for feature extraction of pattern recognition-based myoelectric control,” in Eng. Med. Biol. S. (EMBC), 2015 37th Annu. Int. Conf. IEEE, pp. 7270–7273. Available: https://ieeexplore.ieee.org/document/7320070
[12] I. Haider, M. Shahbaz, M. Abdullah, and M. Nazim, “Feature Extraction for Identification of Extension and Flexion Movement of Wrist using EMG Signals,” in Electr. Comput. Eng. (CCECE), 2015 IEEE 28th Can. Conf., pp. 792–795. Available: https://ieeexplore.ieee.org/document/7129375
[13] J. Liu, “Feature dimensionality reduction for myoelectric pattern recognition: A comparison study of feature selection and feature projection methods,” Med. Eng. Phys., vol. 36, no. 12, pp. 1716–1720, 2014. Available: https://doi.org/10.1016/j.medengphy.2014.09.011
[14] G. Purushothaman and R. Vikas, “Identification of a feature selection based pattern recognition scheme for finger movement recognition from multichannel EMG signals,” Australas. Phys. Eng. Sci. Med., vol. 41, no. 2, pp. 549–559, 2018. doi: 10.1007/s13246-018-0646-7
[15] N. Nazmi, M. Abdul Rahman, S.-I. Yamamoto, S. Ahmad, H. Zamzuri, and S. Mazlan, “A review of classification techniques of EMG signals during isotonic and isometric contractions,” Sensors, vol. 16, no. 8, p. 1304, 2016. doi: 10.3390/s16081304
[16] M.-K. Kim, M. Kim, E. Oh, and S.-P. Kim, “A review on the computational methods for emotional state estimation from the human EEG,” Comput. Math. Methods Med., vol. 2013, 2013. doi: 10.1155/2013/573734
[17] R. M. Rangayyan, Biomedical Signal Analysis. New Jersey: John Wiley & Sons, 2015.
[18] P. Onsy, A. Alim, M. Moselhy, and E. F. Mroueh, “EMG Signal Processing and Diagnostic of Muscle Diseases,” in 2012 6th Int. Conf. New Trends Inf. Sci. Serv. Sci. Data Mining (ISSDM), pp. 1–6. Available: https://ieeexplore.ieee.org/document/6462866
[19] M. H. Jali, T. A. Izzuddin, Z. H. Bohari, H. I. Jaafar, and M. N. M. Nasir, “Pattern recognition of EMG signal during load lifting using Artificial Neural Network (ANN),” in Control Syst., Comput. Eng. (ICCSCE), 2015 IEEE Int. Conf., pp. 172–177. Available: https://ieeexplore.ieee.org/abstract/document/7482179
[20] M. Sood, “A novel module based approach for classifying epileptic seizures using EEG signals,” in Ind. Inform. Comput. Syst. (CIICS), 2016 Int. Conf., pp. 3–7. Available: https://ieeexplore.ieee.org/document/7462406
[21] N. Jiang, J. L. G. Vest-Nielsen, S. Muceli, and D. Farina, “EMG-based simultaneous and proportional estimation of wrist/hand kinematics in uni-lateral trans-radial amputees,” J. Neuroeng. Rehabil., vol. 9, no. 1, p. 42, 2012. doi: 10.1186/1743-0003-9-42
[22] X. Zhang, X. Li, O. W. Samuel, Z. Huang, P. Fang, and G. Li, “Improving the robustness of electromyogram-pattern recognition for prosthetic control by a postprocessing strategy,” Front. Neurorobot., vol. 11, p. 51, 2017. DOI: 10.3389/fnbot.2017.00051
[23] R. Merletti and D. Farina, Surface Electromyography: Physiology, Engineering, and Applications. New Jersey: John Wiley & Sons, 2016.
[24] D. Stegeman and H. Hermens, “Standards for surface electromyography: The European project Surface EMG for non-invasive assessment of muscles (SENIAM),” Enschede Roessingh Res. Dev., pp. 108–112, 2007.
[25] L. Logesparan, A. J. Casson, and E. Rodriguez-Villegas, “Assessing the impact of signal normalization: Preliminary results on epileptic seizure detection,” in Eng. Med. Biol. Soc., EMBC, 2011 Ann. Int. Conf. IEEE, pp. 1439–1442. doi: 10.1109/IEMBS.2011.6090356
[26] J. Wang, L. Tang, and J. E. Bronlund, “A pattern recognition system for myoelectric based prosthesis hand control,” in. Ind. Electron. Appl. (ICIEA), 2015 IEEE 10th Conf., pp. 830–834. doi: 10.1109/ICIEA.2015.7334225 ·
[27] A. López-Delis, A. F. Ruiz-Olaya, T. Freire-Bastos, and D. Delisle-Rodríguez, “A comparison of myoelectric pattern recognition methods to control an upper limb active exoskeleton,” in Iberoamer. Congr. Pattern Recogn., 2013, pp. 100–107. Available: https://link.springer.com/content/pdf/10.1007%2F978-3-642-41827-3_13.pdf
[28] S. Negi, Y. Kumar, and V. M. Mishra, “Feature extraction and classification for EMG signals using linear discriminant analysis,” in Adv. Comput. Commun. Autom. (ICACCA) Int. Conf., 2016, pp. 1–6. doi: 10.1109/ICACCAF.2016.7748960
[29] A. López-Delis and A. F. Ruiz Olaya, “Métodos computacionales para el reconocimiento de patrones mioeléctricos en el control de exoesqueletos robóticos: una revisión,” INGE@ UAN-Tenden. Ing., vol. 3, no. 5, 2013. Available: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwiwzrLBlMvqAhXFhOAKHZPXAcwQFjAAegQIBBAB&url=http%3A%2F%2Frevistas.uan.edu.co%2Findex.php%2Fingeuan%2Farticle%2Fdownload%2F262%2F204&usg=AOvVaw3PTVXBDATNfynSdIuzJGcT
[30] M. A. Oskoei and H. Hu, “Myoelectric control systems: A survey,” Biomed. Signal Process. Control, vol. 2, no. 4, pp. 275–294, 2007. Available: https://doi.org/10.1016/j.bspc.2007.07.009
[31] Z. Arief, I. A. Sulistijono, and R. A. Ardiansyah, “Comparison of five time series EMG features extractions using Myo Armband,” in Electron. Symp. (IES), 2015 Int., pp. 11–14. Available: https://ieeexplore.ieee.org/document/7380805
[32] M. Haris, “EMG signal based finger movement recognition for prosthetic hand control,” in Commun. Control Intell. Syst. (CCIS), 2015. Available: https://ieeexplore.ieee.org/document/7437907
[33] B. S. Zheng, M. Murugappan, S. Yaacob, and S. Murugappan, “Human emotional stress analysis through time domain electromyogram features,” in Indu. Electron. (ISIE), IEEE Int. Symp., 2013, pp. 172–177. Available: https://ieeexplore.ieee.org/document/6738989
[34] S. V. Vaseghi, Advanced Digital Signal Processing and Noise Reduction. New Jersey John Wiley & Sons, 2008.
[35] L. Ljung, System Identification: Theory for the User, 2nd ed. Up. Saddle River, NJ: PTR Prentice-Hall, 1999.
[36] A. Subasi, “Medical decision support system for diagnosis of neuromuscular disorders using DWT and fuzzy support vector machines,” Comput. Biol. Med., vol. 42, no. 8, pp. 806–815, 2012. doi: 10.1016/j.compbiomed.2012.06.004
[37] K. Englehart, B. Hudgins, P. A. Parker, and M. Stevenson, “Classification of the myoelectric signal using time-frequency based representations,” Med. Eng. Phys., vol. 21, no. 6, pp. 431–438, 1999. Available: https://doi.org/10.1016/S1350-4533(99)00066-1
[38] G. Strang and T. Nguyen, Wavelets and Filter Banks. Wellesley: Cambridge Press, 1996.
[39] T. Kamali, R. Boostani, and H. Parsaei, “A multi-classifier approach to MUAP classification for diagnosis of neuromuscular disorders,” IEEE Trans. Neural Syst. Rehabil. Eng., vol. 22, no. 1, pp. 191–200, 2014. doi: 10.1109/TNSRE.2013.2291322
[40] R. Kohavi, “A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection,” in Int. Joint Conf. Artificial Intell., 1995, pp. 1137–1143. Available: http://ai.stanford.edu/~ronnyk/accEst.pdf
[41] S. Haykin, Neural Networks and Learning Machines. New Jersey: Prentice Hall, 2009.
[42] A. Akhtar, L. J. Hargrove, and T. Bretl, “Prediction of distal arm joint angles from EMG and shoulder orientation for prosthesis control,” in Eng. Med. Biol. Soc. (EMBC), 2012 Annu. Int. Conf. IEEE, pp. 4160–4163. Available: doi: 10.1109/EMBC.2012.6346883
[43] R. S. Naoum, N. A. Abid, and Z. N. Al-Sultani, “An enhanced resilient backpropagation artificial neural network for intrusion detection system,” Int. J. Comput. Sci. Netw. Secur., vol. 12, no. 3, p. 11, 2012.
[44] S. Abe, Support Vector Machines for Pattern Classification, vol. 2. Berlín: Springer, 2005.
[45] J. Yousefi and A. Hamilton-Wright, “Characterizing EMG data using machine-learning tools,” Comput. Biol. Med., vol. 51, pp. 1–13, 2014. doi: 10.1016/j.compbiomed.2014.04.018
[46] L. R. Quitadamo et al., “Support vector machines to detect physiological patterns for EEG and EMG-based human: Computer interaction; A review,” J. Neural Eng., vol. 14, no. 1, p. 11001, 2017. doi: 10.1088/1741-2552/14/1/011001
[47] A. Alkan and M. Günay, “Identification of EMG signals using discriminant analysis and SVM classifier,” Expert Syst. Appl., vol. 39, no. 1, pp. 44–47, 2012. doi: 10.1016/j.eswa.2011.06.043
[48] P. Konar and P. Chattopadhyay, “Bearing fault detection of induction motor using wavelet and Support Vector Machines (SVMs),” Appl. Soft Comput., vol. 11, no. 6, pp. 4203–4211, 2011. doi: 10.1016/j.asoc.2011.03.014
[49] G. L. Prajapati and A. Patle, “On performing classification using SVM with radial basis and polynomial kernel functions,” in 2010 3rd Int. Conf. Emerging Trends Eng. Technol., 2010, pp. 512–515. Available: https://ieeexplore.ieee.org/document/5698379
[50] P. A. Kaplanis, C. S. Pattichis, D. Zazula, and others, “Multiscale entropy-based approach to automated surface EMG classification of neuromuscular disorders,” Med. Biol. Eng. Comput., vol. 48, no. 8, pp. 773–781, 2010. doi: 10.1007/s11517-010-0629-7
[51] G. R. Naik, D. K. Kumar, and others, “Twin SVM for gesture classification using the surface electromyogram,” IEEE Trans. Inf. Technol. Biomed., vol. 14, no. 2, pp. 301–308, 2009. Available: https://ieeexplore.ieee.org/document/5353702
[52] X. Li, Q. Huang, J. Zhu, W. Sun, and H. She, “A novel proportional and simultaneous control method for prosthetic hand,” J. Mech. Med. Biol., vol. 17, no. 08, p. 1750120, 2017. doi: 10.1142/S0219519417501202
[53] H. Shim, H. An, S. Lee, E. H. Lee, H. Min, and S. Lee, “EMG pattern classification by split and merge deep belief network,” Symmetry, vol. 8, no. 12, p. 148, 2016. doi: 10.3390/sym8120148
[54] A. Phinyomark, P. Phukpattaranont, and C. Limsakul, “Feature reduction and selection for EMG signal classification,” Expert Syst. Appl., vol. 39, no. 8, pp. 7420–7431, 2012. doi: 10.1016/j.eswa.2012.01.102
Author notes
a Corresponding author. E-mail: alvaro.orjuela@urosario.edu.co
Additional information
How to cite this article: M. A. Fajardo-Perdomo, V. Guardo-Gómez, A. D. Orjuela-Cañón, and A. F. Ruiz-Olaya, “Classification of the angular position during wrist flexion-extension based on EMG signals,” Ing. Univ., vol. 25, 2021 [Online]. https://doi.org/10.11144/Javeriana.iued25.capd



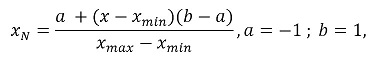 (1)
(1)


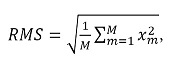 (2)
(2)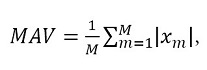 (3)
(3)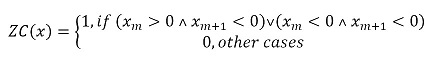 (4)
(4)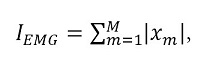 (5)
(5)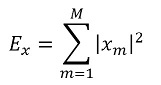 (6)
(6)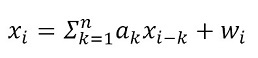 (7)
(7)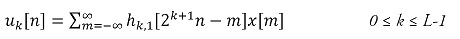 (8)
(8)





