Introduction
Centrifugal pumps are reversible machines that, depending on the direction of rotation of the impeller, can operate as pumps or as turbines. In the latter condition, the pumps are called Pumps working as Turbines or PaTs. PaTs are versatile turbomachines that can have many fields of application, among which the following can be mentioned: electricity generation in aqueduct distribution networks [1] and irrigation systems [2], replacement of pressure regulating valves [3], reverse osmosis processes and replacement of throttling devices in industrial systems [4] and energy storage in microscale [5]. The characterization of a pump with the four-quadrant curve makes it possible to know the behavior of the turbomachine in all its operating modes and to identify those operation zones where hydrodynamic phenomena may occur.
Hydrodynamic phenomena such as Rotating Stall (RS) can affect the turbomachines performance in terms of efficiency reduction, presence of high-pressure pulses and raising vibrations level [6]. Even though the RS inception has not been fully understood [7], [8], the phenomenon shows two characteristics widely mentioned in the scientific literature. First, it appears at off-design conditions, and second, it is a subsynchronous phenomenon [6], [8]–[11].
RS identification has been associated with discontinuities or slope changes in the turbomachines characteristics curves [6], [8]–[13] and has been associated with hysteresis. Flow recirculation in a centrifugal pump impeller [14] was related to hysteresis in its characteristic curve at low flow operation zone. In this case, hysteresis measurement was used to estimate efficiency losses in the studied pump.
On the other hand, the characterization of the RS (understood as its location within the turbomachine, its displacement within it and the determination of its rotation cells number) has been mainly performed with spectral analysis and phase analysis of signals obtained from pressure sensors [6], [9], [10] conveniently placed on the impeller and/or on the volute. Alternative methods considering speed signals acquisition such as LDV [8], [12], or non-intrusive methods with accelerometers [11], have also been used for the identification of the phenomenon. Computational techniques such as CFD are being widely used in the characterization of this phenomenon in turbomachines [10], [15]–[17].
Under laboratory conditions it has been possible to characterize the RS [6], [9], [10] and, sometimes, to see it [9], [11]. However, in many cases, visualization is not possible and the external cues of hydraulic machines, such as noise and vibration, are not enough to clearly identify it. Hence, the use of techniques or methods for their identification and characterization are utmost important. Thus, the main objective of this investigation was the identification and characterization of the RS in a specific low-speed centrifugal pump, considering its four-quadrant characteristic curve. Among the techniques used to characterize the RS, the following can be mentioned: dimensionless characteristic curves, spectral analysis [6], [9]–[11] and phase analysis [6], [10]. These techniques were used to achieve an approximation to the characterization of the phenomenon. Although the phenomenon of interest is RS, the techniques proposed to its characterization may give clues to identify other phenomena at subsynchronous level. Among these phenomena one can mention the vortex rope, fluid-induced rotordynamic forces, surge and auto-oscillation. Each of them needs additional techniques for clear identification, which are beyond the scope of this study. Nevertheless, the present investigation establishes the possibility of the existence of these phenomena in the turbomachine of interest.
Materials and Methods
Test Rig
The test rig is part of the hydraulics laboratory of Eafit University and consists of a closed circuit of pipes connected to a tank and a channel. The energy to move the water within the hydraulic system is supplied by recirculating pumps. The direction in which the flow is addressed inside the loop makes it possible to simulate the conditions of the hydraulic head, either to operate a turbomachine as a pump or as a turbine. A simplified sketch of the test rig is shown in figure 1.
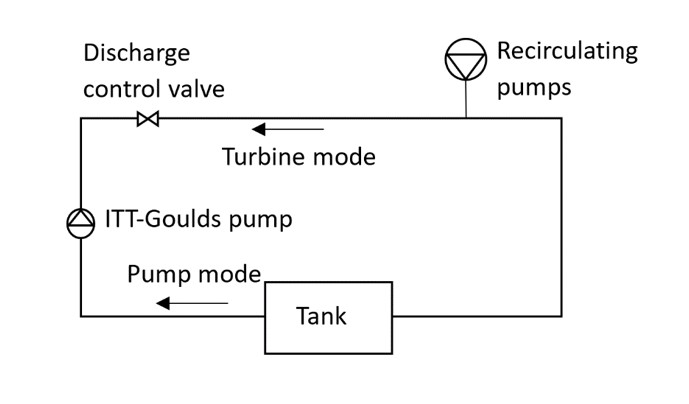 Figure 1.
Test rig sketch
Figure 1.
Test rig sketch
Source: Own elaboration
Pump under study was an ITT-Goulds Pump of 1.5 HP and manufactured in 316 stainless steel. Its main technical specifications are displayed in table 1. The pump was operated in a frequency range from 380 to 1751 rpm in pump mode and from 351 to 1902 rpm in turbine mode. Different rotation speeds were imposed with a frequency driver.
Instrumentation
Instrumentation used to perform the tests was as follows:
-
[1] Wika A-10 piezoresistive pressure transducers in the high- and low-pressure zones.
-
[2] Dytran 2005V piezoelectric pressure transducer in the volute.
-
[3] Futek PMP300 piezoresistive pressure transducer in the volute, placed 30 degrees from the Dytran 2005V piezoelectric pressure transducer.
-
[4] Kistler 8704B50M1 accelerometer installed on the volute.
-
[5] Futek TRS600 FSH01998 torque sensor placed on the pump shaft.
-
[6] General Electric (GE) TransPort PT878 ultrasonic flow meter mounted on the 6-inch pipe in the high-pressure zone.
-
[7] An optical sensor (DT2234C+) was mounted pointing towards the shaft of the machine. A reflective mark on the shaft served as the key phasor.
From now on, the sensors mounted on the volute will be called as follows: The Dytran 2005V as PES (Piezo Electric Sensor), the Futek PMP300 as PRS (Piezo Resistive Sensor) and the Kistler 8704B50M1 as accelerometer. Figure 2 shows the location of the measuring instruments and figure 3 the polar location of PRS and PES.
Table 1.
ITT-Goulds Pump technical specifications
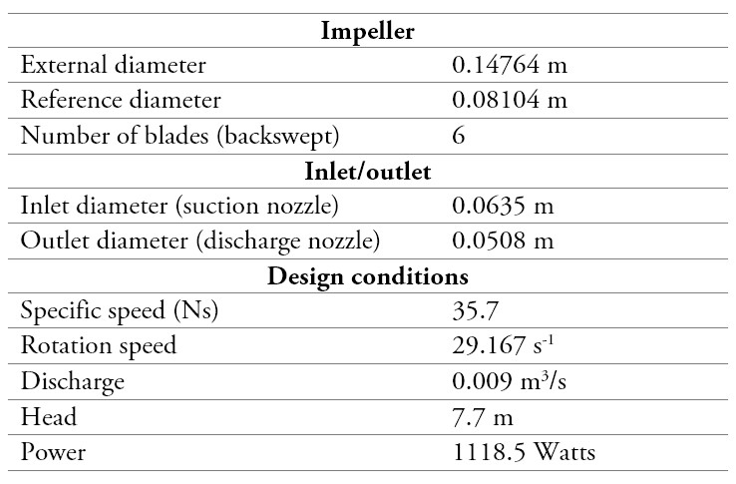
Source: Own elaboration
Data Acquisition Equipment
Electrical signals transmitted by the sensors were received and processed by a National Instruments® CompactRio® 9076 Data Acquisition Equipment (DAE) and a software called Turbologger, developed in a LabView® environment by researchers from EAFIT University. The DAE was configured with four acquisition modules: Two NI-9232, one NI-9215 and one NI-9203. General technical specifications of the modules are shown in [18].
All signals were logged simultaneously and composed of 655360 data for each one of the variables at each operation point (OP). Operation points (OPs) were obtained by varying the impeller rotational speed and the flow rate. Between consecutive OPs the speed varied among 1 and 20 rpm and the flow rate among 0.1 and 0.2 l/s. Sampling rate was 20480 Hz. Acquired signals were used to observe harmonic phenomena within the alias-free band ranging from 0.03 Hz (fundamental Fourier frequency) and 10240 Hz (Nyquist frequency). Current and voltage signals were converted to engineering units of the International System of Units (SI).
 Figure 2.
Location of the instruments used in the measurements
Figure 2.
Location of the instruments used in the measurements
Source: Own elaboration
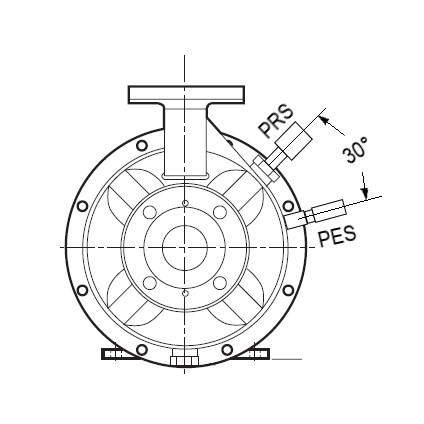 Figure 3.
Polar location of PRS and PES
Figure 3.
Polar location of PRS and PES
Source: Adapted from ITT Goulds Pumps [19]
Characteristic Curves
A convenient way to characterize all operation modes of a centrifugal pump is through the four-quadrant curve proposed by Knapp in 1937, which relates rotation speed and discharge [20]. The four-quadrant curve used in this investigation differs from Knapp’s in the use of dimensionless numbers, velocity and discharge factors, nED and QED respectively, defined as established by IEC-60193 [13]. In addition to this, characteristic curves of velocity (nED) vs. torque (TED) factors, velocity (nED) vs. power (PED) factors and energy (EnD) vs. flow (QnD) coefficients were made. Dimensionless factors and coefficients were also estimated according to the same standard. Factors and coefficients definitions involved in the characteristic curves are presented in equations (1)–(6).
Where, n is rotational velocity (s-1), D is reference diameter (m), Q is discharge (m3/s), E is specific energy (Nm/kg), T is torque (Nm), ρ is density (kg/m3) and P stands for the power (Nm/s).
The characteristic curves were built with 335 points located in all possible modes of operation of the turbomachine under study.
Spectral Analysis
Spectral analysis was performed on the signals from pressure sensors installed in the volute (PES and PRS) and for all OPs considered in the characteristic curves. The pressure signals were converted to their corresponding pressure fluctuation coefficients, 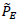 , defined by equation (7), according to IEC-60193 [13].
, defined by equation (7), according to IEC-60193 [13].
Where, p is pressure (N/m2) and is the average pressure (N/m2)
Frequencies were also represented as dimensionless coefficient, fn, defined by equation (8), agreeing with the standard IEC-60193 [13].
Spectral analysis was based on the Fast Fourier Transform of pressure signals. Frequency band from 0 to 2.5 times the rotation speed of the machine was regarded; i.e., 0 ≤ fn ≤ 2.5. The spectral components clearly identified by the two sensors in the volute at the same frequency were taken under consideration. From this information, spectral behavior patterns were determined for each quadrant in the QED-nED characteristic. Procedure details carried out can be found in [21].
Phase Analysis
The wave number, k, is estimated from the phase analysis. k is useful for determining the number of rotating cells and rotation speed in the case of Rotating Stall [10]. However, this estimate might be ambiguous since the frequency of passage of the phenomenon (fpg) perceived by a sensor is either the effect of the passage of one cell rotating at high speed or the effect of several cells rotating at low speeds [22]. This ambiguity can be resolved with the graph of the cross-correlation of the pressure signals, previously filtered, as proposed by Best, LaFlamme and Moffatt [22], and Fortin and Moffat [23]. The proposal of these authors consists of identifying pairs of consecutive peaks with the greatest correlations, which represent the period mark of the hydrodynamic phenomenon. Then, counting the oscillations between these peaks corresponds to k. Nevertheless, the application of the method is not always suitable because the result of cross-correlation of filtered signals does not clearly show the peaks representing the period mark of the phenomenon and counting fluctuations between them becomes a subjective task. In order to overcome this problem, the following relationship was proposed between the phase angle estimated by the Fourier coefficients on the original signals, i.e. unfiltered signals, and the polar angle separating the two sensors on the volute. This is referred as the k-Fourier-coefficients method.
Where,
-
kθ: Wave number estimated by the k-Fourier-coefficients method,
-
Δθ: Phase-shift angle estimated by Fourier-coefficients, and
-
θG: Polar angle separating the sensors on the volute.
Deduction of equation (9) is shown in [21]. It was assumed that cells rotate at a constant speed and if several cells are present, they are equidistant.
To validate the k-Fourier-coefficients method, k was also estimated by filtering the signals and then calculating the cross-correlation of the signals. In this validation the pressure signals were filtered with digital bandpass filters that were chosen in such a way that they did not significantly affect the response of the signals in phase or amplitude. The filters regarded were Elliptic, Butterworth, Chebyshev type 1 and type 2 and Kaiser. The validation can be seen in [21].
For the analysis of rotating cells, k was adjusted according to the following hypotheses: First, the wave number is an integer number of stall cells that occupies the circular domain. Second, the passage frequency perceived by the sensors (fpg
) is equal to the wave number by the frequency of the phenomenon (f), w.r.t. an inertial frame of reference [22]. Third, in order to fulfill the above hypothesis, it is necessary to correct the value of the frequency of the phenomenon (f) to guarantee that:
In terms of frequency coefficients, equation (10) is written as:
Phase analysis was performed for some components identified in the spectral analysis at operating points such as best efficiency, minimum torque, change of slope sign on the QED-nED characteristic and those representing significant variations in pressure fluctuation.
Subsynchronous Phenomena
-
Rotating Stall: It can be defined as a flow disturbance in a turbomachine resulting from backflows that partially or totally block the channels between the rotor blades. The backflows are associated with flow shedding at the solid-fluid interphase due to alterations in the angle of attack of the flow when it enters the channels between the blades. In turbines it is common to find RS at frequencies from 0.5 to 0.7 times the rotation frequency of the rotor [24]. In pumps, RS can be found at frequencies between 0.05 and 0.10 times the rotation frequency of the rotor [8, 28].
-
Surge and auto-oscillation: Surge is a disturbance involving all components of a hydraulic system, which causes pressure and flow rate fluctuations throughout the system. When this type of disturbance is associated with cavitation it is called auto-oscillation [24]. The literature reviewed does not point out the typical frequencies of the surge in hydraulic turbomachines.
-
Vortex rope: This phenomenon is generated in the draft tube of turbines and consists of a swirl with a low-pressure core where cavitation occurs. The vortex core has a helical shape with a precession frequency of 0.25 to 0.35 times the rotation frequency of the rotor [25]. In the case of PaT’s, it can be seen in the low-pressure pipe since it works as a draft tube.
-
Fluid-induced rotordynamic forces: This phenomenon occurs when the rotation axis of the rotor-shaft system is slightly displaced from its mid-position by effects of the fluid. The rotodynamic forces will be a function of the frequency of the rotor, but not of the displacement [26]. It is common that this phenomenon appears at subsynchronous frequency [24].
Results
Characteristic Curves
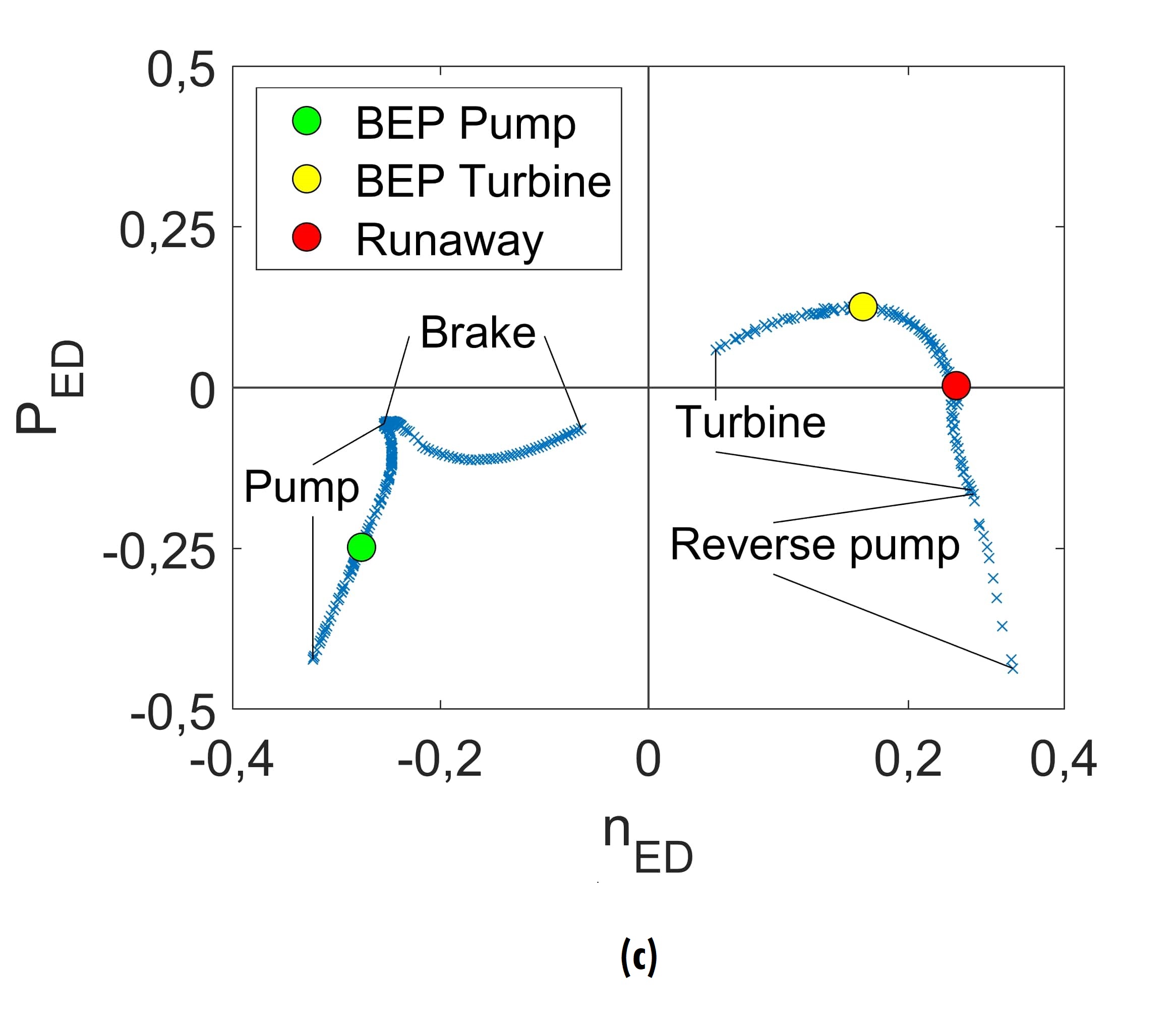
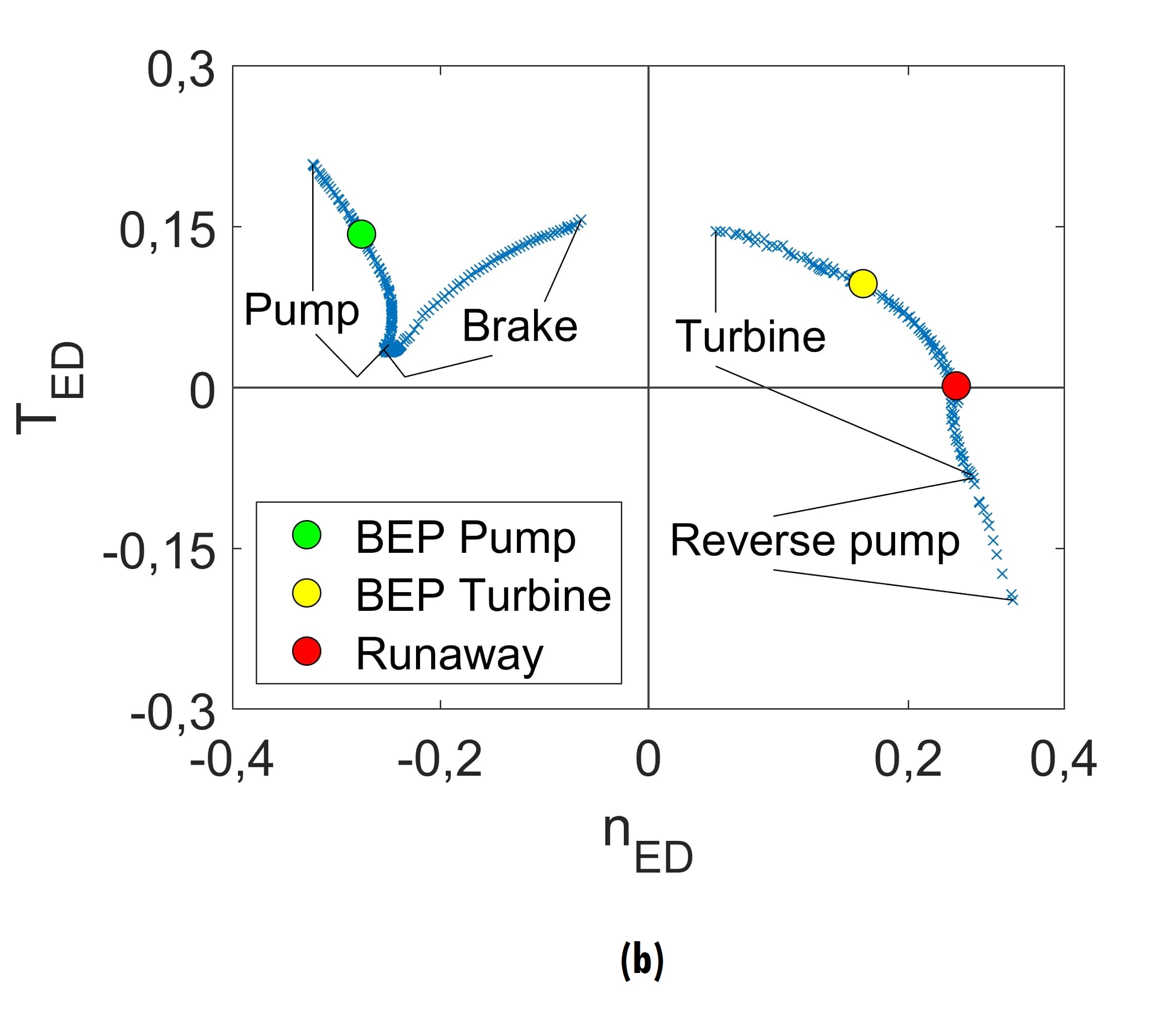
Figure 4 depicts characteristic curves QED-nED (figure 4a), TED-nED (figure 4b) and PED-nED (figure 4c). Table 2 presents the values of speed factor, flow factor, torque factor and power factor for the Best Efficiency Point (BEP) in pump mode, the BEP in turbine mode and the runaway.
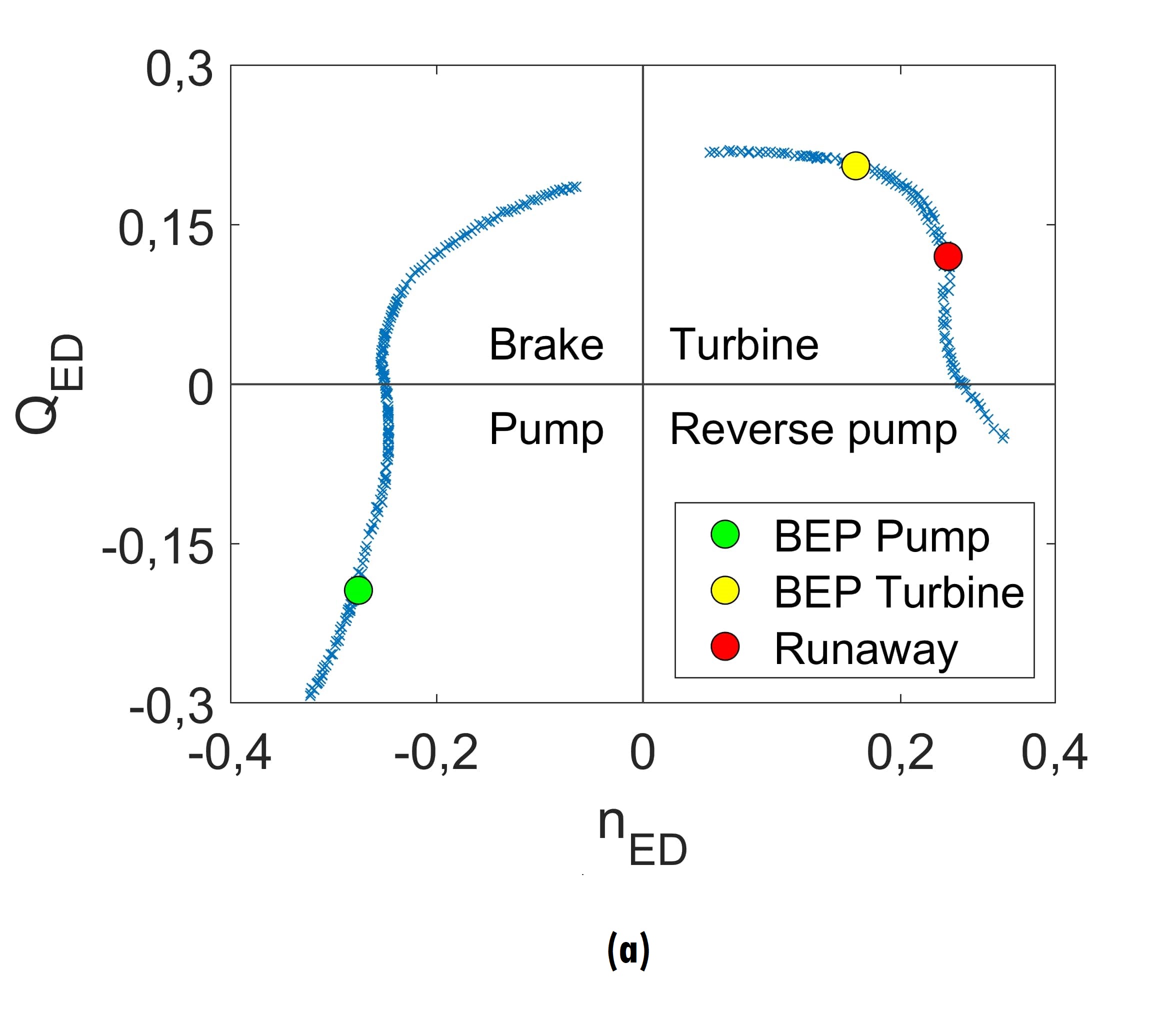 Figure 4.
Characteristic curves of the pump under study
Figure 4.
Characteristic curves of the pump under study
Source: Own elaboration
QED-nED characteristic is properly called the four-quadrant curve, which are pointed out in figure 4a. The first quadrant corresponds to a pump, the second to a brake, the third to a turbine and the fourth to a reverse pump. The runaway point splits the third quadrant into two regions: turbine and brake turbine. [13]. In the case of the TED-nED and PED-nED curves, their quadrants do not correspond directly to the quadrants of the QED-nED characteristic (see figures 4b and 4c).
Table 2.
Speed, flow, torque and power factors of the relevant points of the characteristic curves

Source: Own elaboration
Spectral Analysis
Figure 5 illustrates spectral patterns as a function of frequency and flow coefficients for the PES signals in the band 0 ≤ fn ≤ 2.5. The spectra of the BEP in pump mode, BEP in turbine mode and runaway were highlighted. In quadrants 1, 2 and 3 a 2D representations QED vs fn are added too. Since only matching spectra were taken from the PES and PRS sensors, it is not necessary to display the PRS graph. Spectral components of the PES and PRS signals only differ in amplitude. The amplitude of the spectral components obtained by PRS signals was greater than that of the PES signals in most cases.
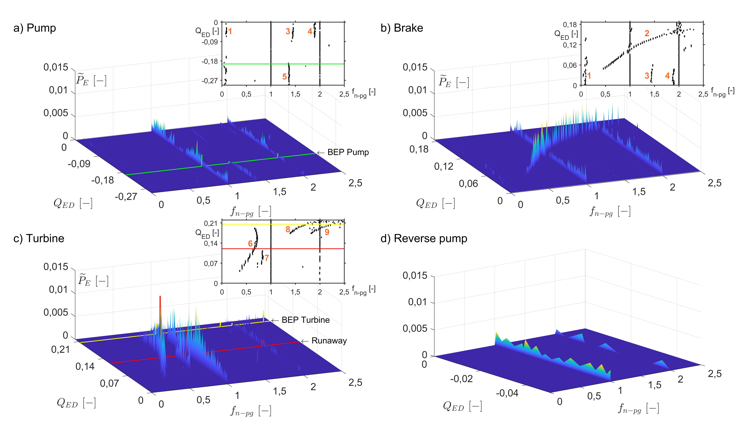 Figure 5.
Spectral patterns in the QED-nED characteristic curve obtained from PES signals
Figure 5.
Spectral patterns in the QED-nED characteristic curve obtained from PES signals
Source: Own elaboration
Spectral components 1X and 2X are present in all operation modes, albeit they are not evenly distributed along the whole range of flow coefficients. Component 1X represents the shaft frequency and 2X emerges from non-sinusoidal excitations at the shaft frequency [24]. Description of the other spectral patterns is shown in table 3.
Table 3.
Description of the spectral patterns
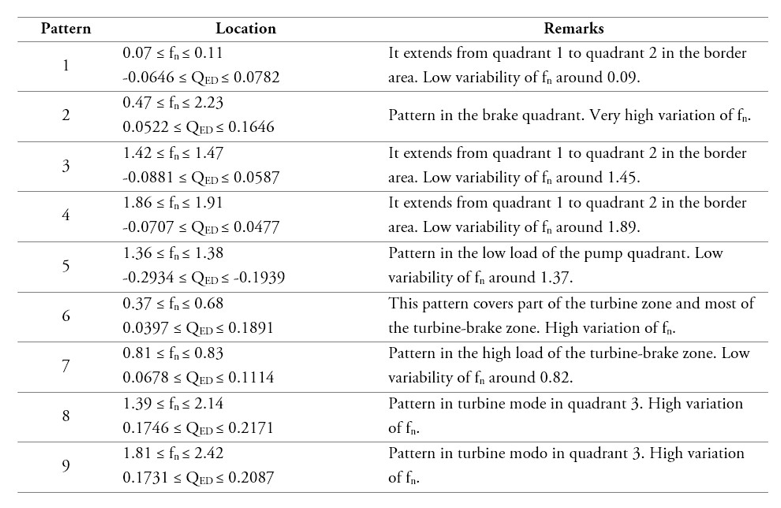
Source: Own elaboration
Phase Analysis
Phase analysis was focused on the calculation of k-number by the k-Fourier-coefficients method (kθ
) on some spectral components identified in spectral analysis. Most of these components are part of the spectral patterns depicted in figure 5.
Twelve OPs were selected from the QED-nED characteristic curve for the phase analysis. The cross-correlation of the PES and PRS signals was computed to identify the most highly correlated spectral components for the selected OPs. Figure 6 shows the cross spectrum of the two signals with the spectral components considered in the phase analysis.
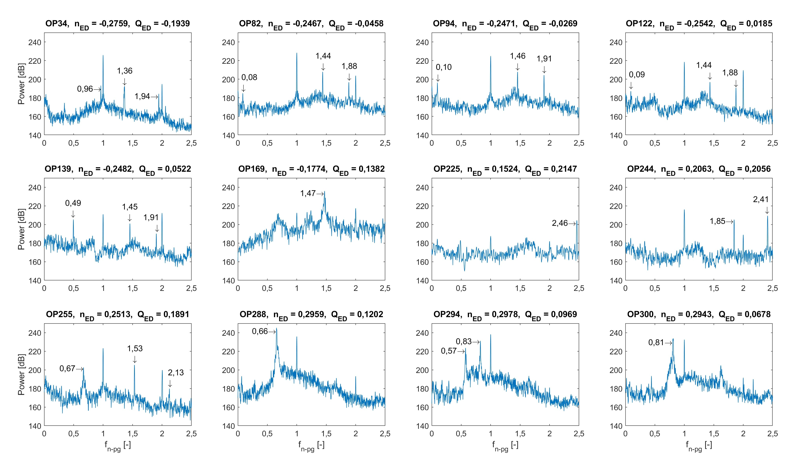 Figure 6.
Cross-spectra of PES and PRS signals
Figure 6.
Cross-spectra of PES and PRS signals
Source: Own elaboration
A chart depicting the spectra of 12 representative OPs on the QED-nED characteristic curve is given in figure 7. It highlights the matching spectral components of PES (black spectra) and PRS (red spectra) and it shows each component of interest with its frequency detected by the sensors (fn-pg), its k-number and the frequency of the hydrodynamic phenomenon (fn). Spectral components fn = 1 and fn = 2 are not shown in the graph. Figures 8a and 8b display the location of the same 12 OP in the TED-nED and PED-nED characteristics, respectively.
The discrepancies between the spectra of the two sensors mounted on the volute (see figure 7) are given by the type of sensor. The PRS is a sensor used mainly for industrial process control and measures total pressure values, while the PES is a highly sensitive sensor used to measure pressure variations with respect to the average (pressure fluctuations). While the PRS can measure phenomena with frequencies up to 250 Hz, the PES can measure dynamic phenomena up to 40 KHz. Although the two sensors are very different, it is important to mention that the frequency range considered in this investigation was from 1 to 79.25 Hz, which is within the span of the two sensors.
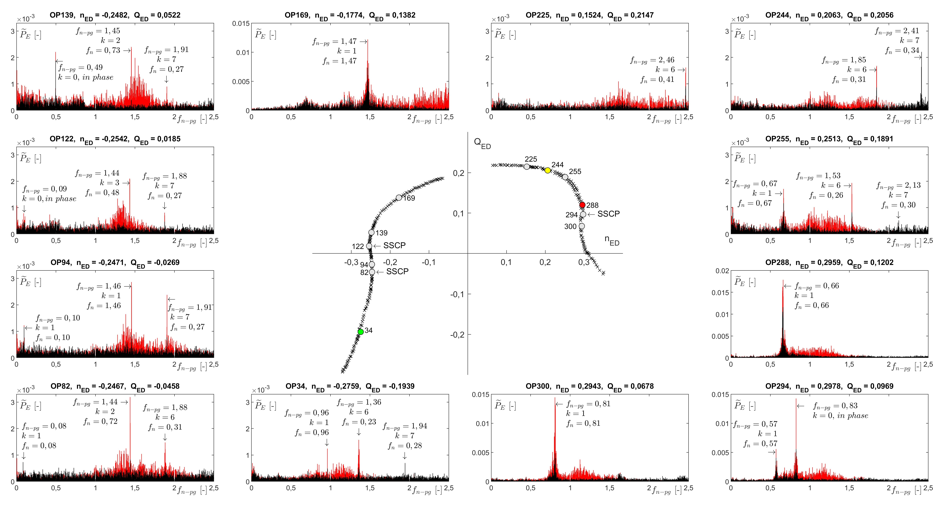 Figure 7.
QED-nED characteristic curve and some representative operating points with their corresponding amplitude spectra
Figure 7.
QED-nED characteristic curve and some representative operating points with their corresponding amplitude spectra
Source: Own elaboration
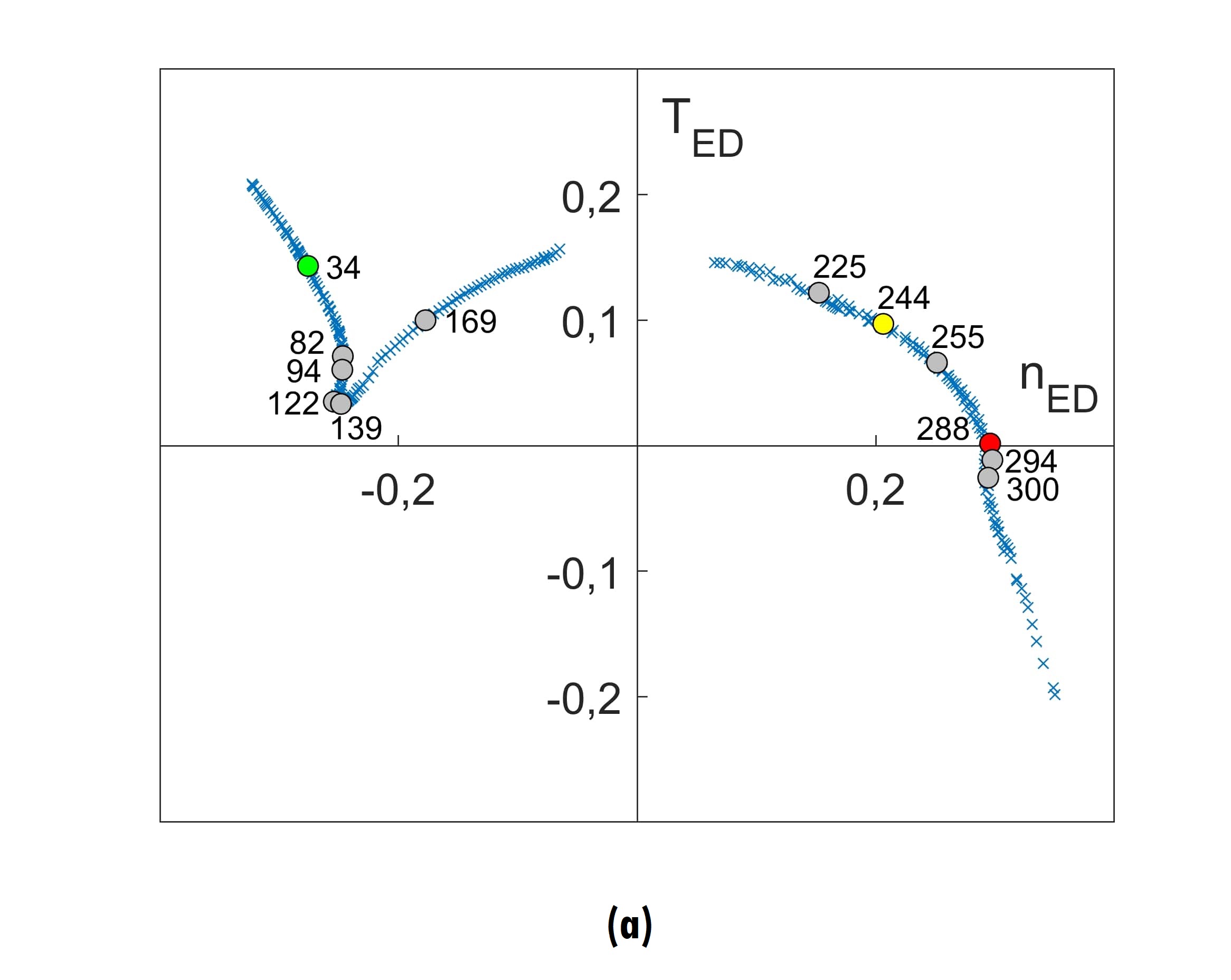 Figure 8.
TED-nED and PED-nED characteristics with 12 operating points highlighted
Figure 8.
TED-nED and PED-nED characteristics with 12 operating points highlighted
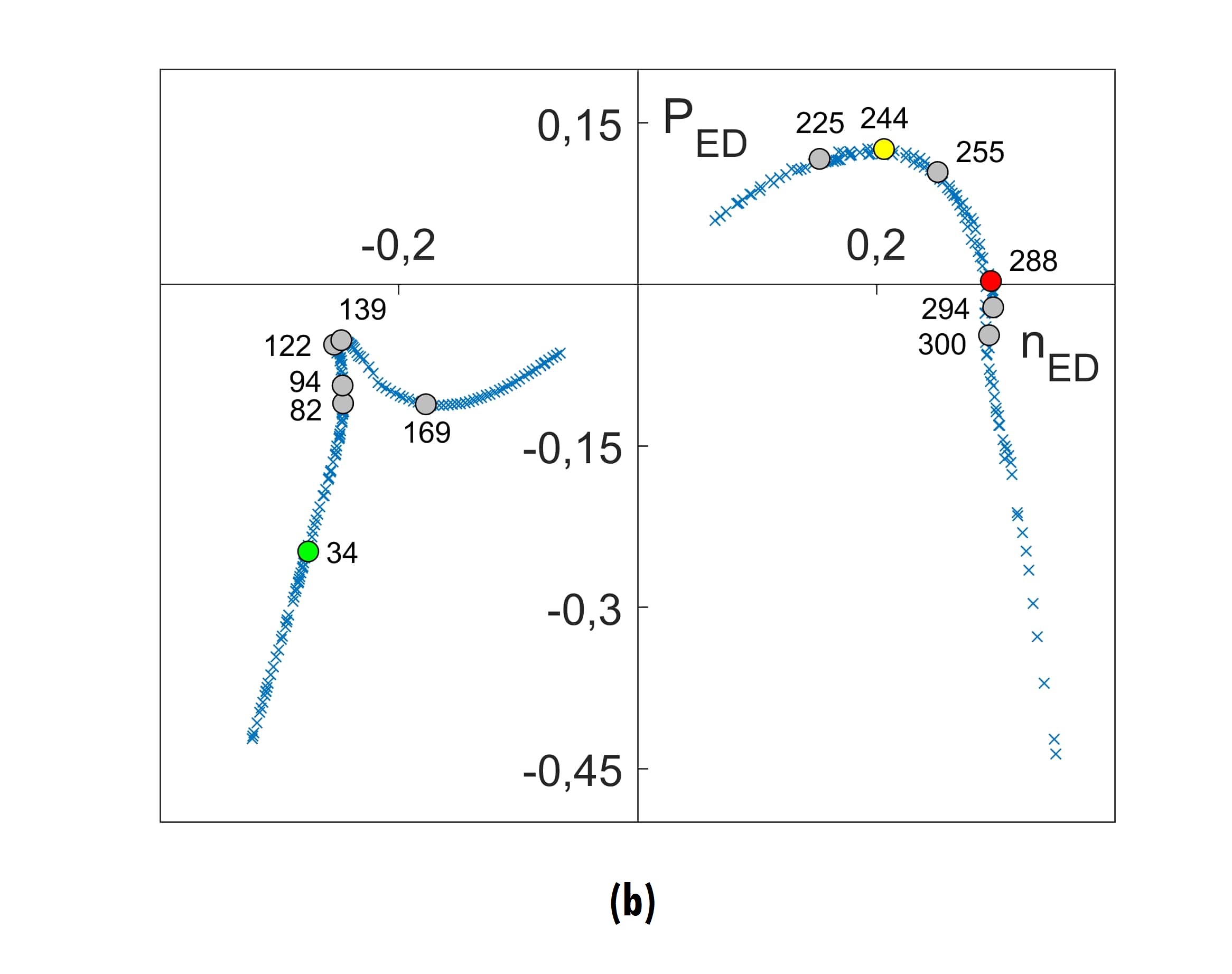
Source: Own elaboration
It is important to notice that in the time domain the relationship between fn and k-number can be seen using correlation of the filtered signals [22], [23]. Figure 9 shows an example of the correlation between the PES and PRS signals for a spectral component fn = 1.85 in OP244 (BEP Turbine) with n = 18.3452 Hz. This graphical representation will be referred from now on BB-Plot (Bolaños-Botero Plot) since the contribution from the authors. The strips represent the period of the phenomenon (T) and the number of peaks or valleys into each strip corresponds well to k. The time differential between consecutive peaks corresponds to the passage period (Tpg), i.e., the period perceived by the sensor. The results shown in equations (12) and (13) can be estimated from figure 9.
Each strip in figure 9 contains 6 peaks or valleys, which means that k = 6. Hence the frequency of the phenomenon can be computed by dividing equation (13) by k, yielding what is presented in equation (14).
As expected, the passage frequency computed from the passage period estimated by the BB-Plot corresponds to the frequency identified in the spectrum of the sensors mounted in the volute (see figures 6 y 7).
The power of this approach lies in the ability to feature the period of the phenomenon that, as can be seen, is not evident in the bare graph of the cross correlation. This is a significant improvement to the graphical method proposed by Best, LaFlamme and Moffatt [22], and Fortin and Moffat [23], which is inappropriate for this case.
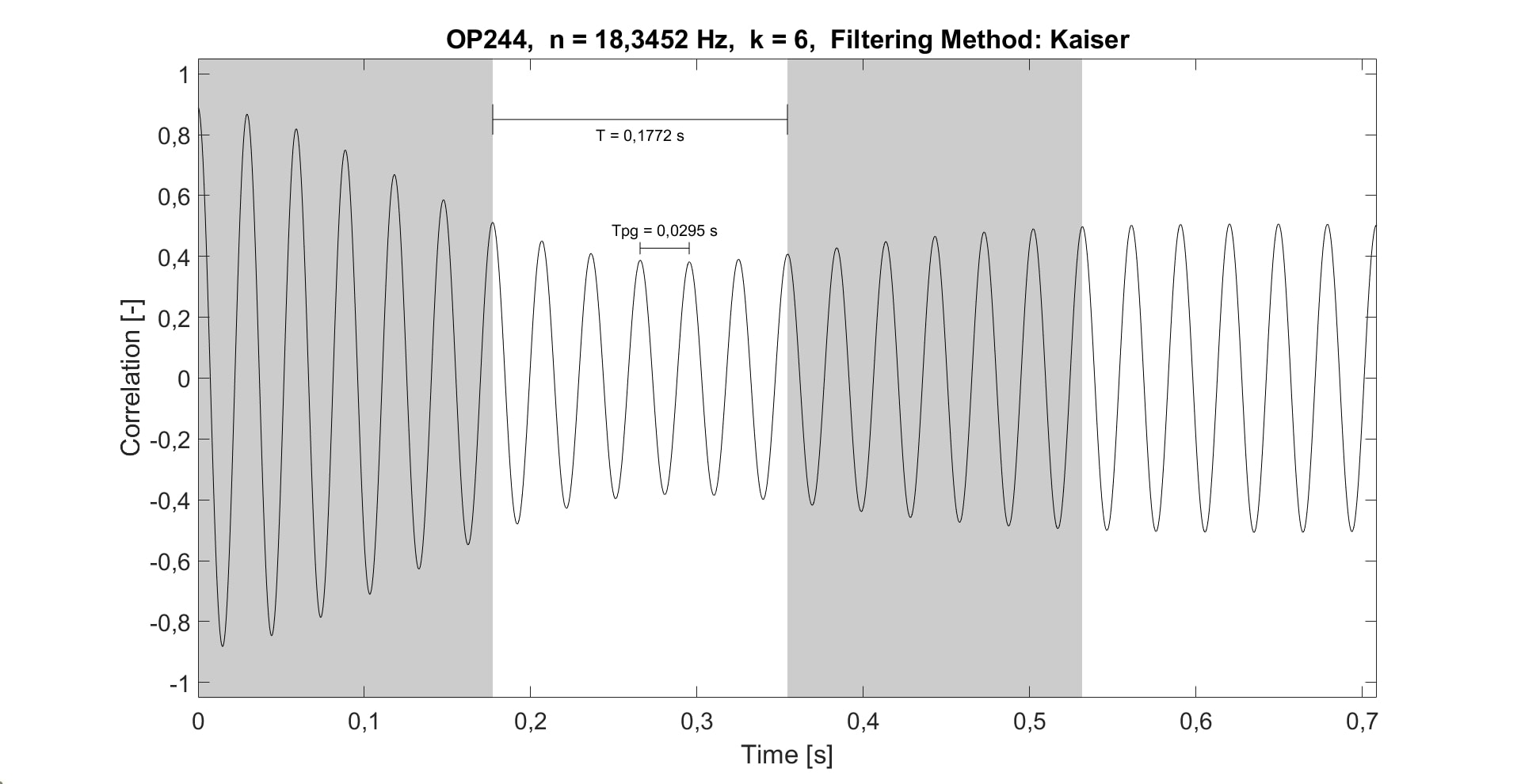 Figure 9.
BB-Plot
Figure 9.
BB-Plot
Source: Own elaboration
Acceleration and Pressure Fluctuation Analysis
Pressure fluctuations and acceleration may be indicative of hydrodynamic phenomena [27]. In order to identify possible areas of operation of the turbomachine under study with the presence of this type of phenomena, the results of the spectral patterns (figure 5), the components of interest (figure 6) and the location of the OPs highlighted in the characteristic curves (figures 7 and 8) were related with the RMS curves of the PES and accelerometer versus QnD. Figure 10 shows the PES and accelerometer RMS curves and the possible operating zones (OZ) with hydrodynamic phenomena.
OZ 1
A periodic phenomenon predominates with fn_pg = 1.37 and k = 6 in an interval of QED between 0.1938 and 0.2934 (pattern 5 of figure 5). The frequency of the phenomenon is about 23 % of the frequency of the rotor. The evidence gathered in the laboratory and the reviewed literature do not suggest the existence of RS in this zone. In quadrant 1 RS would be expected in the zone of high heads and low flows [24], [27]. Being a phenomenon that occurred in all the OPs in the QED range already indicated and discarding the existence of RS for the reason previously exposed, it is presumed that the spectral component is associated with rotodynamic forces induced by the fluid, which can occur at subsynchronous level [24].
OZ 2
This area corresponds to the border between quadrants 1 and 2 (patterns 1, 3 and 4 of figure 5). It starts at the SSCP in quadrant 1 (OP82) and ends at the lowest torque point in quadrant 2 (OP139). This area has spectral components around fn = 0.09, some in phase (see OP122 in figure 7) and some not (see OP82 and OP94 in figure 7). According to [8], [28], the RS occurs in centrifugal pumps at frequencies of 5 to l0 % of machine rotation (0.05 < fn < 0.10), which would be in accordance with the results obtained. On the other hand, according to [27], two conditions can be identified that are indicative of RS. The first is the gradual increase and decrease of the pressure pulses (bell shape) as a function of QnD; and the second, the spectral components related to RS have similar phase-shift angles in the zone. The first condition can be seen in figure 10a. The second condition is satisfied with OP82 and OP94. However, the existence of one component in phase in the OP139 (point of minimum torque in pump mode) also suggests the existence of Surge, if it is considered that authors such as Day [7] point out that Surge and SR are related and in some cases one of the phenomena precedes the other. The OPs with evidence of RS exhibit a wave number (k) equal to one, suggesting that if the phenomenon occurs, it would have one rotating cell.
OZ 3
Strong vibrations are present from OP139 to the last OP in quadrant 2 (see figure 10a) with the particularity that fn-pg changes as QnD increases. The evidence gathered in the laboratory and the literature reviewed does not allow to draw a conclusion about the type of hydrodynamic phenomenon that could explain this behavior, but an eventual RS is ruled out because there is no zone with onset, development and decay of the pressure fluctuations, characteristic of this phenomenon [9], [11], [27]. Figure 10a shows, on the one hand, the RMS of pressure fluctuations with a pronounced growth from OP139 to OP169, and thereafter, a very slight drop to the last operating point of the quadrant 2 (OP203). On the other hand, the RMS of the accelerometer signals shows a permanent increase from OP139 to OP203 (pattern 2 of figure 5).
OZ 4
Figure 10b shows an area of increases and decreases in pressure pulses in the range 0.752 ≤ QnD ≤ 1.409 (between OP225 and OP255), with uniform levels of vibration. This zone is characterized by OPs with sharp spectral components ranging from fn = 1.8 to fn = 2.45, with k between 3 and 7, suggesting subsynchronous rotating phenomena at fn between 0.30 and 0.71. The spectral components frequency and the shape of the zone state the existence of RS, however, the place where it is located is not usual for this phenomenon. According to the literature, RS is expected in the turbine-brake zone [9], [11], [27], [29]. As no other evidence is available, the existence of RS in this area cannot be suggested. Further investigations may elucidate this issue.
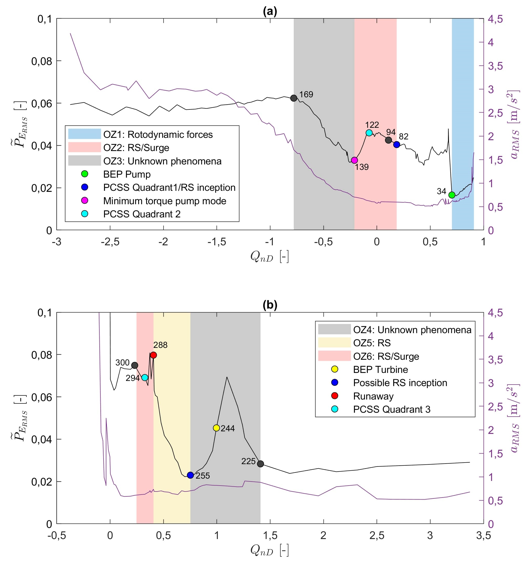 Figure 10.
(a) RMS of the PES and accelerometer signals in the pump and pump-brake operating modes, and (b) RMS of the PES and accelerometer signals in the turbine, turbine-brake and reverse pump operating modes
Figure 10.
(a) RMS of the PES and accelerometer signals in the pump and pump-brake operating modes, and (b) RMS of the PES and accelerometer signals in the turbine, turbine-brake and reverse pump operating modes
Source: Own elaboration
OZ 5
This zone corresponds to the grey strip in figure 10b with spectral components typical of an RS (55 % to 71 % of the impeller rotation speed), with k = 1 and phase-shift angles between 20.5° and 24.1°, which are close to the angle of separation between the pressure sensors placed in the volute. In pump-turbines operating in turbine mode, RS rotation frequencies have been reported in around the 70 % of the impeller rotation in the runaway speed [9], or by the 59 % in the turbine-brake zone near the runaway condition [29], which would be in accordance with the results obtained. For the runaway there is a frequency of 66 % of the impeller frequency and near the runaway (OP294), in the turbine-brake zone, of 57 %.
OZ 6
This zone exhibits spectral components around fn = 0.82, some of them in phase (k = 0) and others not (k = 1). This zone is represented in figure 10b as a yellow strip. The in-phase phenomenon can be described as pressure and flow oscillations involving the entire hydraulic system, thus a surge or auto-oscillatory phenomenon [27] while the non-phase one fits well with a one-cell RS. This symbiosis is not unexpected considering that the two phenomena have been intimately linked in compressors, and until the 50’s of the 20th century no clear differentiation had been made between the two types of perturbations [7].
The spectrum for OP294 corresponds to the PCSS in quadrant 3 (see figure 7) and shows two components that point, on the one hand, the presence of an RS (fn = 0.57 and k = 1), and, on the other hand, the presence of a surge (fn = 0.83 and k = 0). According to Day [7], both types of disturbances can occur at the same point of instability in a compression system. The evidence collected suggests therefore that this might occur as well in hydraulic systems.
Additional Remarks
-
[1] Quadrant four did not display spectral components of interest other than fn = 1 and fn = 2 (see figure 5). However, it is important to notice that the high-pressure pulses and high vibrations are experienced in this quadrant. Figure 10b was deliberately trimmed on the vertical scale to maintain the aspect ratio with figure 10a. However, from QnD = 0, and below, the pressure pulses increase vertiginously. In the case of the RMS of a maximum value of 3.37 was reached, and for the RMS of the acceleration a value of 9.45 m/s2.
-
[2] The Vortex rope was observed in some OP in the lower part of the turbine mode and in the upper part of the turbine brake mode (OP 280 to OP294). However, the spectra of these points did not exhibit typical components for this phenomenon, which according to Escaler et al [25] are between 0.25 and 0.35 times the rotation frequency of the rotor. It is assumed that the location of the pressure sensors did not allow the detection of this phenomenon using the spectra.
Conclusions
Results allow to draw these main conclusions:
-
[1] This research collected evidence to define at least three areas of interest where the occurrence of RS and/or Surge is suggested. First area, between quadrant 1 and 2 (OZ2), with components in the range 0.083 ≤ fn ≤ 0.096 some of them in-phase and others not. Second one, in the lower part of turbine mode (OZ5), prior to runaway, exhibits spectral components out-of-phase in the range 0.51 ≤ fn ≤ 0.71. Third area, in turbine-brake mode (OZ6), with spectral components in the range 0.81 ≤ fn ≤ 0.84. This area is the most controversial because the evidence exposes that in two operating points coexist simultaneously two hydrodynamic phenomena, one in phase and the other not. This type of behavior has been reported in compressors [7] but not in pumps as turbines.
-
[2] The classical method proposed by Best, LaFlamme and Moffatt [22], and Fortin and Moffat [23] to identify visually the k-number is unsuitable in some conditions. This limitation was overcome with the BB-plot which is a variant to the cross-correlation method.
-
[3] A quantitative method to estimate the wave number, referred to as the k-Fourier-coefficients is introduced. It is a feasible alternative to determine the wave number k, with the great advantages of not requiring time domain signal pre-processing; i.e., saving time and computational resources. The wave number allows discriminating a RS and corresponds, at the same time, to the number of stall rotating cells.
-
[4] The spectral pattern observed in quadrant two (pattern 2), where the frequency coefficient increases as the flow coefficient increases, can become a line of investigation since this type of behavior cannot be explained according to the literature reviewed. Moreover, considering that k in many of the spectral components of this pattern are in the order of 6 or 7, these subsynchronous phenomena require their identification and characterization.
-
[5] The results obtained from the study of this pump can be applied to another pump if the laws of geometric, kinematic and dynamic similarity among the two turbomachines are met.
Acknowledgments
The authors would like to thank the Hydraulics Laboratory, the Metrology Laboratory and the GEMI Research Group of Eafit University for all the support given to this research.”
References
[1] M. Rossi, M. Righetti, and M. Renzi, “Pump-as-Turbine for energy recovery applications: The case study of an aqueduct,” Ener. Procedia, vol. 101, pp. 1207–1214, Nov. 2016. Available: https://doi.org/10.1016/j.egypro.2016.11.163
[2] M. Crespo et al., “Potential energy recovery using micro‐hydropower technology in irrigation networks: Real‐world case studies in the south of Spain,” Proceedings, vol. 2, no. 11, Aug. 2018, Art. no. 679. doi: 10.3390/proceedings2110679
[3] M. Patelis, V. Kanakoudisa, and K. Gonelas, “Pressure management and energy recovery capabilities using PATs,” Proc. Eng., vol. 162, pp. 503–510, Nov. 2016. Available: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=&ved=2ahUKEwjmo7CWycntAhXwdN8KHZnKA08QFjAAegQIARAC&url=https%3A%2F%2Fcyberleninka.org%2Farticle%2Fn%2F1466062.pdf&usg=AOvVaw0r9fgCYVqRDpRNKPIJWbxe
[4] B. Orchard and S. Klos, “Pumps as turbines for water industry,” World Pumps, pp. 22–23, Aug. 2009. doi: 10.1016/S0262-1762(09)70283-4
[5] A. Morabito and P. Hendrick, “Pump as turbine applied to micro energy storage and smart water grids: A case study,” App. Energy, vol. 241, pp. 567–579, May. 2019. doi: 10.1016/j.apenergy.2019.03.018
[6] S. Berten, P. Dupont, L. Fabre, M. Kayal, and F. Avellan, “Experimental investigation of flow instabilities and rotating stall in a high-energy centrifugal pump stage,” in Proc. ASME FEDSM2009, Vail, Colorado, USA, 2009, pp. 505–513. Available: https://doi.org/10.1115/FEDSM2009-78562
[7] J. Day, “Stall, surge, and 75 years of research,” J. Turbomach., vol. 138, Jan. 2016, Art. no. 011001. vailable: https://doi.org/10.1115/1.4031473
[8] U. Ullum et al., “Prediction of rotating stall within an impeller of a centrifugal pump based on spectral analysis of pressure and velocity data,” J. Phys. Conf. Ser., vol. 52, pp. 36–45, 2006. doi: 10.1088/1742-6596/52/1/004
[9] V. Hasmatuchi, M. Farhat, S. Roth, F. J. Botero, and F. Avellan, “Experimental evidence of rotating stall in a pump-turbine at off-design conditions in generating mode,” J. Fluids Eng., vol. 133, no. 5, May 2011, Art. no. 051104. doi: 10.1115/1.4004088
[10] O. Braun, “Part load flow in radial centrifugal pumps,” Ph.D. thesis, Lab. de Mach. Hyd., EPFL, Lausanne, Suisse, 2009.
[11] F. Botero, V. Hasmatuchi, S. Roth, and M. Farhat, “Non-intrusive detection of rotating stall in pump-turbines,” Mech. Sys. Sig. Process., vol. 48, no. 1-2, pp. 162–173, Oct. 2014.
[12] D. A. Johnson, N. Pedersen, and C. B. Jacobsen, “Measurements of rotating stall inside a centrifugal pump impeller,” in Proc. ASME FEDSM2005, Houston, Texas, USA, 2005, pp.1281–1288. Available: https://doi.org/10.1115/FEDSM2005-77313
[13] Hydraulic turbines, storage pumps and pump-turbines-Model acceptance tests, CEI/IEC 60193, 1999.
[14] K. Kaupert and T. Staubli, “The unsteady pressure field in a high specific speed centrifugal pump impeller—Part II: Transient hysteresis in the characteristic,” J. Fluids Eng., vol. 121, no. 9, pp. 627–632, Sep. 1999. Available: https://doi.org/10.1115/1.2823515
[15] Y. Fu et al., “Numerical and experimental analysis of flow phenomena in a centrifugal pump operating under low flow rates,” J. Fluids Eng., vol. 137, no. 1, Jan. 2015, Art. no. 011102. Available: https://doi.org/10.1115/1.4027142
[16] Lei, C. et al., “Numerical investigation on the rotating stall characteristics in a three-blade centrifugal impeller,” in Proc. IMECE2016, Phoenix, AZ, USA, 2016, Art. no. 65794.
[17] N. Zhang, M. Yang, B. Gao, Z. Li, and D. Ni, “Unsteady pressure pulsation and rotating stall characteristics in a centrifugal pump with slope volute,” Adv. Mech. Eng., vol. 6, Feb. 2015, Art. no. 710791. Available: https://doi.org/10.1155/2014/710791
[18] NI, “Módulos CompaqRio”. https://www.ni.com/es-co/shop/hardware/compactrio-modules-category.html#
[19] G&L Series SSH-C and SSH-F Installation, Operation and Maintenance Instructions, ITT Goulds Pumps. Available: https://manualsbrain.com/es/manuals/1065761/
[20] R. T. Knapp, “Complete characteristics of centrifugal pumps and their use in the prediction of transient behavior,” ASME Transac., pp. 683–689. Nov. 1937. Available: https://authors.library.caltech.edu/48235/1/Complete%20Characteristics%20of%20Centrifugal%20Pumps%20and%20Their%20Use%20in%20the%20Prediction%20of%20Transient%20Behavior.pdf
[21] H. Bolaños, “Fenómenos hidrodinámicos periódicos en una bomba centrífuga de baja velocidad específica,” M.S. thesis, Esc. Ing., Universidad Eafit, Medellín, Colombia, 2018. Available: https://repository.eafit.edu.co/bitstream/handle/10784/12998/Hern%E1nDar%EDo_Bola%F1osArias_2018.pdf?sequence=2
[22] R. Best, J. G. C. LaFlamme, and W. C. Moffatt, “Flow measurements in rotating stall in a gas turbine engine compressor,” in Proc. ASME Gas Turbine Aeroeng. Congr., Amsterdam, The Netherlands, 1988, Art. no. 88-GT-219.
[23] J. Fortin and W. C. Moffatt, “Inlet flow distortion effects on rotating stall,” in Proc. ASME Gas Turbine Aeroeng. Congr. and Expo., Brussels, Belgium, 1990, Art. no. 90-GT-215. Available: https://bit.ly/2W6bDsR
[24] C. E. Brennen, “Pump vibration,” in Hydrodynamics of Pumps, New York, NY, USA: Cambridge University Press, 2011, pp. 137–171.
[25] X. Escaler, E. Egusquiza, M. Farhat, F. Avellan, and M. Coussirat, “Detection of cavitation in hydraulic turbines,” Mech. Sys. Sig. Process., vol. 20, no. 4, pp. 983–1007, May 2006.
[26] R. S. Miskovish and C. E. Brennen, “Some unsteady fluid forces on pump impellers,” J. Fluids Eng., vol. 114, no. 4, pp. 632–637, Dec. 1992. Available: https://doi.org/10.1115/1.2910078
[27] P. Dörfler et al., “Stability-related unsteady phenomena,” in Flow-induced pulsation and vibration in hydroelectric machinery, London, UK: Springer, 2013, pp. 143–161.
[28] M. Sinha, A. Pinarbasi, and J. Katz, “The flow structure during onset and developed states of rotating stall within a vaned diffuser of a centrifugal pump,” J. Fluids Eng., vol. 123, no. 9, pp. 490–499, Sep. 2001. Available: https://doi.org/10.1115/1.1374213
[29] C. Widmer, T. Staubli, and N. Ledergerber, “Unstable characteristics and rotating stall in turbine brake operation of pump-turbines,” J. Fluids Eng., vol. 133, no. 4, Apr. 2011, Art. no. 041101. Available: https://doi.org/10.1115/1.4003874
Notes
*
Research article
Author notes
a Corresponding author. E-mail: hbolanos@eafit.edu.co
Additional information
How to cite this article: H. D. Bolaños, and F. Botero, “Four-quadrant characterization of hydrodynamic phenomena in a low specific speed centrifugal pump,” Ing. Univ., vol. 25, 2021 [Online]. https://doi.org/10.11144/Javeriana.iued25.fchp







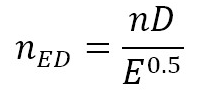 (1)
(1)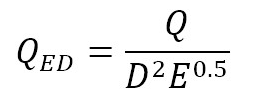 (2)
(2)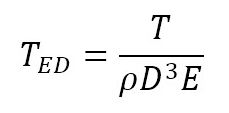 (3)
(3)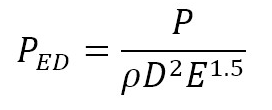 (4)
(4)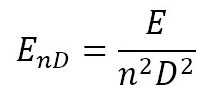 (5)
(5)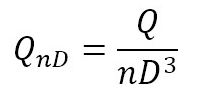 (6)
(6)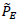 , defined by equation (
, defined by equation (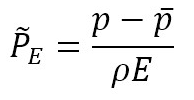 (7)
(7)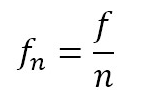 (8)
(8)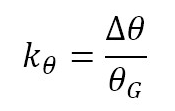 (9)
(9)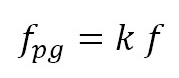 (10)
(10)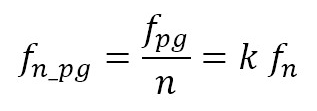 (11)
(11)








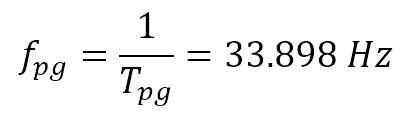 (12)
(12)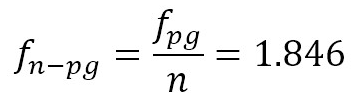 (13)
(13)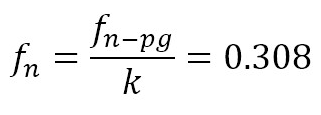 (14)
(14)

