Introduction
According to Human Talent in Health Law [1], a university hospital is defined as a “health service institution that provides university training and is recognized as a hospital of teaching and practices supervised by competent academic authorities providing training and medical care in each level of complexity”. In addition, it states that within the requirements to meet by a university hospital as a training scenario is to have an installed capacity according to the development of health science and training needs of health personnel. In the same way, it must have the space for teaching adequately equipped, that correspond to their training objectives and the number of students [1].
Hospital services are composed by subspecialties where different procedures are carried out. Similarly, a hospital service is split into a set of support processes or activities, for example: scheduled surgery, emergency surgery, outpatient, hospitalization wards, emergency room, etc. The difference between some activities is the physical space in which they occur, so it is possible to group them into families of activities, such as hospitalization.
In the learning process of students, they are assigned to different activities in order to acquire knowledge and develop skills necessary for future practice. Besides days and times when students can be programmed, the assignation depends on the availability of activities and training objectives. Thus, in some activities they can be assigned seven days a week, day and night shifts; while other activities are done on specific days.
However, in developing countries, hospitals where the number of students is not proportional to the number of beds are frequently found, and there is no relation between the number of students and medical teachers to ensure the effectiveness of the program. One of the factors that influences the number of students not matching the installed capacity of health centers is the insufficient amount of practice settings to health education programs demand in the country. This situation affects the training process of students and quality of the service given to patients [2].
Installed capacity for any production or service system refers to necessary infrastructure (physical, human, technological resources, real state, machinery and equipment) to produce certain goods and services. This capacity is directly proportional to the expected amount of production or service [3]. In the hospital environment, installed capacity includes: teaching medical personnel, hospital beds, medical offices, operating rooms, laboratories, and any instrument or equipment used for patient care. Hospital capacity planning is a challenging problem [4]. A Considerable amount of research has been conducted on related problems, such as: different models to assess resource capacity in hospitals, models for bed capacity ([5]–[7]), emergency rooms [8], and human resources [9]. However, it is uncommon to have methods to help the calculation of the number of students in the different service areas at a hospital.
This paper aims to propose a method to assess installed capacity of training scenarios at a university hospital, to determine the number of students who can rotate in the institution, so that the quality of training processes and in-patient care is assured. The next section presents a related literature review. Then, the methodology is introduced and the formulation of the mathematical program is explained. Then the case of General Surgery service at Hospital Universitario Clínica San Rafael is presented, and the proposed methodology is applied. Finally, conclusions are given at the end.
Literature Review
In a hospital environment, different types of personnel exist. The terms “personnel”, “employees”, and “staff” are used synonymously, even though there is a distinction for “nurses”, “physicians”, “residents” and “health care students”, among others. Physicians and nurses are considered already educated with an appropriate amount of years as practitioners. Residents have finished their theoretical education, but are still in practical training, and “Health care students” are still in theoretical education and practical training.
The scheduling problems in the field of health are a vast part of the literature. According to [10] there are three main groups of problems: Staffing, Rostering and Re-planning.
-
Staffing: These problems involve decisions that determine the size of a workforce and clinical rotations of medical residents. “How many people should I employ?”.
-
Rostering: These problems aim to place resources in different shifts subject to different constraints. “When does which employee have to work?”.
-
Re-planning: These problems consist of reorganizing the use of resources in the case of unforeseen events. “Who can substitute for the employee who is unexpectedly absent?”.
The problem studied in this paper can be seen as a combination of Staffing and Rostering. The typical staffing (nurse or medical staff) planning process consist of two major tasks: Forecasting demand on a facility or unit of service and budgeting or allocating personnel over the planning period. The process of allocating personnel is the translation of the forecast of the patients’ demand into a full-time equivalent nurse or medical personnel that is required for each shift in each ward to meet the demand [11]–[13]. It is usual to use techniques from operational research to find a solution to this problem. Most research papers are commonly framed as optimization problems, for example calculating the optimal number of staff to employ such that costs are minimized and assuming that unmet demand is satisfied by using float or external staff [14]–[17].
The resident scheduling problem is a specific case of the multiperiod staff assignment problem where individuals are assigned to a variety of tasks over multiple periods in order to complete their training. Consequently, those programs are often not only time-related but also task-related. Task-related means that residents should perform a given number of different interventions in their program. Typically, a resident will follow a rotation across different clinical departments, where the number of performed interventions per period may be estimated. As in many staffing and training situations, numerous limitations and requirements may be placed on those assignments [18]–[20]. Models developed in the literature determines the number and type of surgical procedures a resident performs each month by assigning surgeries to residents subject to various constraints such as the limited availability of surgeries and the residents’ availability to perform surgical procedures [21], [22].
While the foregoing literature review has revealed many related problems and models dealing with similar scheduling contexts, no analysis exists that adequately deals with the specific nature of the problem. None of these fully addresses the particular staffing and scheduling problem at hand. In the next section, the problem is described in more precise terms, and a method based on a mathematical programming model for it is proposed.
Problem Description and a Solution Method
The problem is to determine the number of students who can rotate in the institution to ensure the quality of training processes and in-patient care. The students must accomplish different activities in order to acquire knowledge and develop skills necessary for future practice. There is limited availability of activities and resources, like devices, machines, equipment or physical space that can be used by a medical teacher or student for patient care. There are different types of activities and they can be assigned to seven days a week, in both day and night shifts; while other activities are done on specific days. The difficulty of determining the number of students per service is that each activity can have a different number of students, and that students should rotate to every service within a specific amount of hours. Because of this, it is difficult to obtain the operation’s highest potential.
In order to find the number of students that the institution can accept, to rotate simultaneously, a three-step procedure is proposed and explained below:
Step 1: Calculation of the Number of Students Allowed per Activity
To calculate the number of students allowed per activity, the methodological proposal by the Ministry of Health and Social Protection [23] is used. This considers the number of practice units (QPU), the number of students allowed per practice unit (SAU), the practice unit usage (PUU) and the practice unit time (PUT), as seen in equation (1). The SAU refers to any device, machine, equipment or physical space that can be used by a medical teacher or student for patient care; for example, hospital beds, laboratories, medical offices, operating rooms, radiology units, and others. Likewise, the relationship that exists between the number of students and practice units is defined as the number of students allowed per practice unit; for instance, five or six students per bed, or two students per operating room. On the other hand, the PPU measures the unit demand as the occupancy time percentage. Finally, the PUT is the rotation length of time, for example, monthly or 6-hour shift.
Step 2. Model: Assignment of Students to Activities at a Hospital Service
A mathematical model is proposed to find the number of students. The model takes into account capacity of activities, schedules and shifts of students, the minimum hours that they must rotate in each activity and other constraints from the teaching-service agreements with Higher Education Institutions.
Then the proposed mathematical model is presented. It is an integer linear programming model that, given a number of students that can rotate simultaneously in service, (set E, in the model), determines whether is feasible their usage in the activities over a time horizon.
Sets:
 : Service activities, indexed in a.
: Service activities, indexed in a.
 : Days, indexed in d.
: Days, indexed in d.
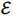 : Students, indexed in e.
: Students, indexed in e.
 : Families of activities, indexed in f.
: Families of activities, indexed in f.
 : Shifts, indexed in s.
: Shifts, indexed in s.
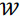 : Weeks, indexed in w.
: Weeks, indexed in w.
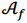 : Activities from the same family f, indexed in a.
: Activities from the same family f, indexed in a.
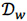 : Days from the same week w, indexed in d.
: Days from the same week w, indexed in d.
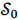 : Night shifts, indexed in s.
: Night shifts, indexed in s.
Parameters:
F: The night shifts maximum frequency.
H: The maximum number of weekly hours.
Hsd: The hours in shift s, on day d.
Las: Students allowed in activity a, in shift s.
Mf: The minimum number of hours in a family of activities f.
Pasd: 1 if the activity a, in shift s, can be programmed on day d.
Variables:
xasd : The number of students in activity a, in shift s, on day d.
yeasd : 1 if the student e rotates in activity a, in shift s, on day d.
Linear Programming Model Description
The objective function (2) maximizes the number of students. The family of constraints (3) counts the number of students per day, activity and shift. Constraints (4) establish that the number of students in each activity cannot exceed the limit of students allowed, which was found in the previous step. Constraints (5) ensure that students can only be assigned to one activity and shift per day. Constraints (6) verify that students are assigned to activities and shifts when they are available. On the other hand, Constraints (7) ensure the lower-bound of hours that students must rotate per family of activities. Similarly, Constraint (8) ensure the upper-bound of weekly hours that students can be in practical training. Constraints (9), (10) and (11) state that students are assigned in night shifts between 1 and 2 times per week, the frequency cannot exceed a certain number of days. Constraints (12) ensures that students must rotate through all activities. Finally, the decision variables are defined in (13) and (14).
Linear programming model:
Subject to:
Step 3. Computation of the Maximum Number of Students per Service
The model proposed in step 2 assumes that the number of students who can be part of training practices in service is known. The model determines whether it is feasible that number of students to satisfy given restrictions. In this step, it is established the maximum number of students who can meet all the constraints. For this purpose, an iterative process in which increases in each iteration the student set size (set ε, in the model) is performed until the model is no longer feasible. The size of the last feasible model is the maximum number of students allowed or the service capacity.
Case of Study
For the purpose of this paper, and in order to illustrate the methodology used to address the problem, the installed capacity for practical training in General Surgery service at Hospital Universitario Clínica San Rafael (HUCSR) is calculated. Only undergraduate students from medicine program will be considered.
HUCSR is a university hospital. In its 90 years of experience, it has established itself as one of the most important health centers in Bogota, Colombia. The clinic has a Research and Education Department that aims to contribute to scientific and technological development in the health field. By producing knowledge and innovation, the Department aims to improve health conditions in Colombia [24]. Thus, in addition to health services, the institution offers academic training to the community, through agreements with Higher Education Institutions, which provides its facilities for conducting training practices in levels of undergraduate, internship, and postgraduate students.
HUCSR, in the process of accreditation as a university hospital, must determine the number of students per program, level of training and health services, so that the best performance in the teaching process and health care is ensured. According to the Manual of Accreditation in Health, Ambulatory and Hospital, the institution must state “the number of people in practical training per user, taking into account respect for patients’ rights, privacy, dignity and security” [25].
Nowadays, HUCSR has several agreements with Higher Education Institutions in more than 20 programs, in training levels of undergraduate, internship and postgraduate students, in which hundreds of students rotate monthly. 47 % of students who rotate are undergraduate (VII to X semester of Medicine) or belong to other training programs, like speech therapy, physiotherapy, psychology, nursing, instrumentalist, and others. 20 % are internship students enrolled in Medicine last year, and the remaining percentage corresponds to postgraduate students (residents), who are performing a specialty.
General Surgery service includes procedures of general, neck and chest surgery. Similarly, the service is divided into Shift, Operating Rooms, Ward Rounds, Emergency Room and Outpatient activities. In Shift, emergency surgeries are performed while scheduled surgeries are performed in Operating Rooms. In Wards and Emergency Room, hospitalized patients are checked, diagnosed and evaluated, thus, the service can be separated into five activities, which are grouped into three families of activities, as shown in figure 1. Besides, in Shift students are assigned seven days a week, daytime (7:00 a. m.-5:00 p. m.) and nighttime (7:00 p. m.-7:00 a. m.); other activities are assigned Monday to Friday daytime only. However, Wednesday and Friday students attend only until noon, because of university activities.
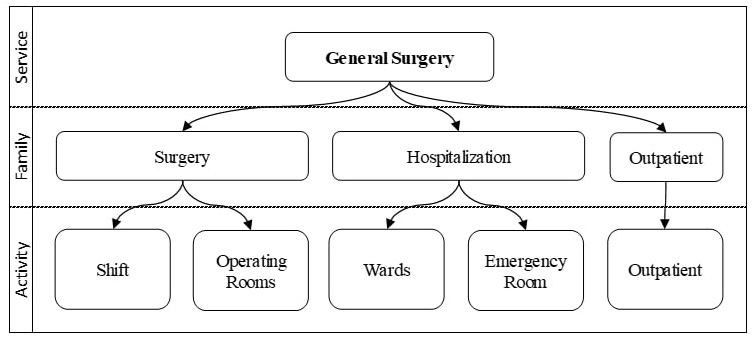 Figure 1
Representation of General Surgery service
Figure 1
Representation of General Surgery service
Source: Own elaboration
Implementation
In order to find the capacity offered by the hospital at the General Surgery service, the previously showed methodology was used.
Step 1: The permissible limits of students per activities are calculated. This information was collected through interviews with experts in the service. Table 1 shows, for each activity, the practice unit used, the number of practice units (QPU) and the number of students allowed per practice unit (SAU). Thus, in all activities, two undergraduate students are allowed. Wards are the only exception given there is capacity for ten students.
Table 1
Number of students allowed per activity
Source: Own elaboration
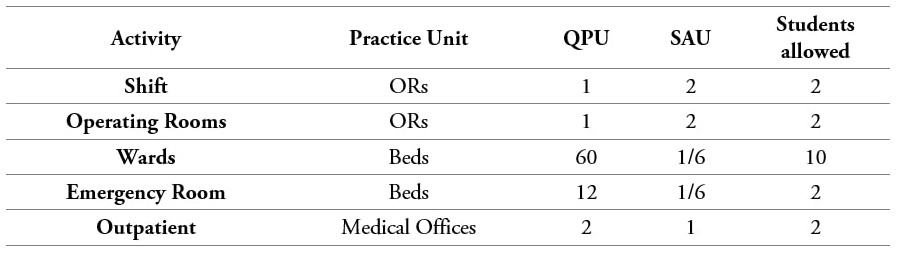
Step 2: The integer linear programming model is executed over a four-week planning horizon (28 days), with five activities, three families of activities and two shifts. To define the minimum hours per family of activities, the practical training plans of teaching-service agreements are used. Similarly, it is stated that the maximum frequency of night shifts is five days. Finally, the maximum weekly hours are established by law. Table 2 presents the parameters used in the linear programming model. The model was solved using free software GLPK, on an Intel® Pentium ® Dual Core, 64 bits, 2.20 GHz speed processors, Windows operating system. The run time per iteration is less than 5 seconds.
Table 2
Model parameters
Source: Own elaboration
Findings
When the number of students is iterated to find the maximum feasible value (step 3), the results stated that the service capacity is eight students. Currently, the hospital mostly rotates six students in the service at a time. Table 3 shows the results from the model (letter D corresponds to day shift and letter N to night shift).
Table 3
Model results
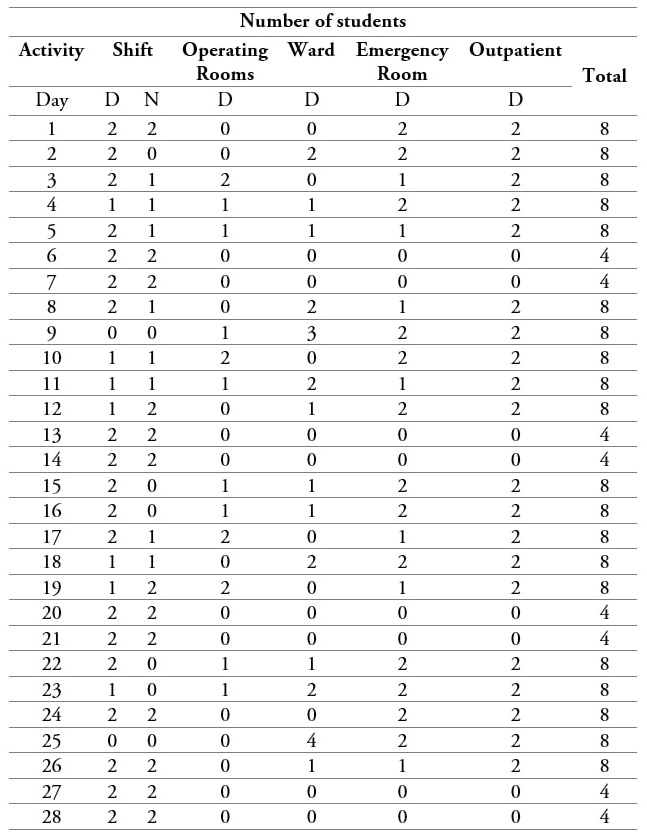
Source: Own elaboration
Sensitivity Analysis
It is important for the hospital to know the effects of critical parameters on capacity found; for this purpose, a sensitivity analysis was performed. First, the minimum hours in Outpatient activity is identified as the critical constraint, so it was decided to change this parameter from zero to 40 hours per month. As a result, service capacity gradually increases up to 13 undergraduate students with a minimum of 20 monthly hours; if the parameter continues to decrease, no change in capacity is observed, as shown in figure 2.
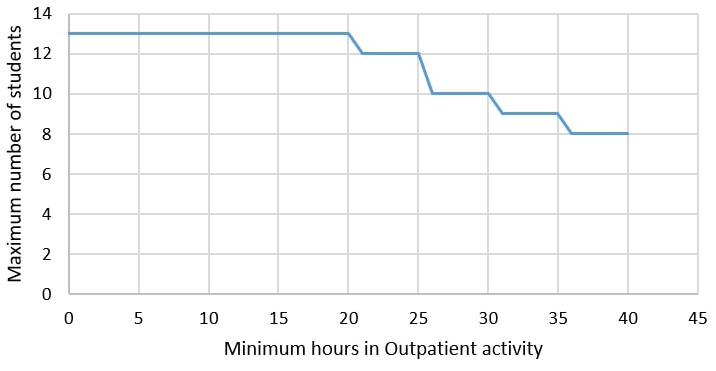 Figure 2
Sensitivity of the number of students
Figure 2
Sensitivity of the number of students
Source: Own elaboration
Similarly, it evaluates changes in the expected number of surgeries per month, while it increases the maximum number of students in the service. This calculation considers that in accordance to institutional norms, in operating rooms nine people maximum are allowed. According to the head of the service, 20 % of surgeries are high-risk procedures, so undergraduate students cannot enter. If surgery is not high risk, equally probable space is available in the operating room for one or two students. Also, based on information provided by Quality and Information Systems area of HUCSR, on average 3.3 surgeries are scheduled and 6.75 emergency surgeries are performed, including general, neck and chest surgery.
Given the initial solution in the model (8 students), they would attend on average to 30.3 surgeries per month. If service capacity increases because of the reduction in the minimum of hours in Outpatient activity, expected surgeries per student decreases to 23.6 for 13 students instance, as shown in figure 3.
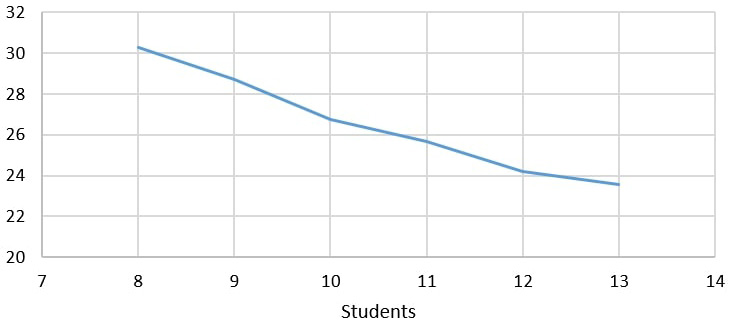 Figure 3
Expected number of surgeries
Figure 3
Expected number of surgeries
Source: Own elaboration
Conclusions
In the field of university hospitals, installed capacity for practical training is an issue of great importance. It influences the training processes, which aims to enable students to approach the practice of Medicine through contact with patients, physical exams and diagnostic tests. Furthermore, the number of students in rotations has an impact on the quality of care, safety and dignity of patients.
In this way, this paper proposes a methodology to determine the number of students per service. For this, on top of the support activities’ capacity, the dynamics of rotation of students and compliance with the restrictions established in agreements with Higher Education Institutions are considered. The methodology was tested with the General Surgery service at Hospital Universitario Clínica San Rafael, aiming for the extension to other services of the institution, as well as other university hospitals.
In the case of the hospital, the hospital did not have a method to calculate the capacity or the number of students that could accept, the proposed method suggested eight students, causing a two students increase in the training capacity (33 %). Other intangibles of the methodology are being able to count on a more agile methodology, reducing the time of planning and the real possibility of extending to other services.
The proposed method finds the ideal number of students to be accepted in practical training in a specific service at the hospital. It also allows, through sensitivity analysis, identifying costs or sacrifices, measured as expected values of access to practice units, which would be incurred if the hospital decides to increase that number.
References
[1] Government of Colombia, “Ley de talento humano en salud. Ley 1164,” Diario Oficial, no. 46.771, 2007. Available: https://www.redjurista.com/Documents/ley_1164_de_2007_congreso_de_la_republica.aspx#/
[2] E. Álvarez and R. Salazar, “Hospitales universitarios y su implicación en la educación médica,” Rev. Med., vol. 35, no. 3, pp. 243–263, 2013. Available: https://revistamedicina.net/ojsanm/index.php/Medicina/article/view/102-7
[3] C. Mejía, “El concepto de la capacidad instalada,” 2013. [Online]. Available: http://www.planning.com.co/bd/valor_agregado/Julio2013.pdf
[4] A. Rais and A. Viana, “Operations research in healthcare: A survey,” Int. Trans. Oper. Res., vol. 18, no. 1, pp. 1–31, 2011. Available: https://doi.org/10.1111/j.1475-3995.2010.00767.x
[5] S. A. Angelo, E. F. Arruda, R. Goldwasser, M. S. C. Lobo, and A. Salles, “Demand forecast and optimal planning of intensive care unit (ICU) capacity,” Pesqui. Oper., vol. 37, no. 2, pp. 229–245, 2017. Available: https://doi.org/10.1590/0101-7438.2017.037.02.0229
[6] P. R. Harper and A. K. Shahani, “Modelling for the planning and management of bed capacities in hospitals,” J. Oper. Res. Soc., pp. 11–18, 2002. Available: https://doi.org/10.1057/palgrave.jors.2601278
[7] A. Kokangul, “A combination of deterministic and stochastic approaches to optimize bed capacity in a hospital unit,” Comput. Methods Programs Biomed., vol. 90, no. 1, pp. 56–65, 2008. doi: 10.1016/j.cmpb.2008.01.001
[8] F. F. Baesler, H. E. Jahnsen, and M. DaCosta, “Emergency departments I: The use of simulation and design of experiments for estimating maximum capacity in an emergency room,” in Proc. 35th Conf, Winter Simul. Driving Innovat., 2003, pp. 1903–1906.
[9] C. A. Amaya, N. Velasco, and S. Aguirre, “Planning and scheduling an emergency room workforce using linear programming,” Int. J. Math. Game Theory, Algebr., vol. 23, no. 4, p. 373, 2014.
[10] M. Erhard, J. Schoenfelder, A. Fügener, and J. O. Brunner, “State of the art in physician scheduling,” Eur. J. Oper. Res., vol. 265, no. 1, pp. 1–18, Feb. 2018. doi: 10.1016/j.ejor.2017.06.037
[11] V. L. Smith‐Daniels, S. B. Schweikhart, and D. E. Smith‐Daniels, “Capacity management in health care services: Review and future research directions,” Decis. Sci., vol. 19, no. 4, pp. 889–919, 1988.
[12] E. S. Buffa, M. J. Cosgrove, and B. J. Luce, “An integrated work shift scheduling system,” Decis. Sci., vol. 7, no. 4, pp. 620–630, 1976.
[13] C. E. Saville, P. Griffiths, J. E. Ball, and T. Monks, “How many nurses do we need? A review and discussion of operational research techniques applied to nurse staffing,” Int. J. Nurs. Stud., 2019. doi: 10.1016/j.ijnurstu.2019.04.015.
[14] K. L. Maass et al., “Incorporating nurse absenteeism into staffing with demand uncertainty,” Health Care Manag. Sci., vol. 20, no. 1, pp. 141–155, Mar. 2017. doi: 10.1007/s10729-015-9345-z
[15] M. Bam, Z. Zhang, B. Denton, M. P. Van Oyen, and M. Duck, “Planning models for skills-sensitive surgical nurse staffing,” 2017. Available: https://ssrn.com/abstract=2959005 or http://dx.doi.org/10.2139/ssrn.2959005
[16] A. Gunawan and H. C. Lau, “Master physician scheduling problem,” J. Oper. Res. Soc., vol. 64, no. 3, pp. 410–425, 2013. Available: https://doi.org/10.1057/jors.2012.48
[17] R. Bruni and P. Detti, “A flexible discrete optimization approach to the physician scheduling problem,” Oper. Res. Health Care, vol. 3, no. 4, pp. 191–199, 2014. Available: http://www.dis.uniroma1.it/~bruni/files/bruni14orhc.pdf
[18] H. D. Sherali, M. H. Ramahi, and Q. J. Saifee, “Hospital resident scheduling problem,” Prod. Plan. Control, vol. 13, no. 2, pp. 220–233, 2002.
[19] L. S. Franz and J. L. Miller, “Scheduling medical residents to rotations: Solving the large-scale multiperiod staff assignment problem,” Oper. Res., vol. 41, no. 2, pp. 269–279, 1993. Available http://dx.doi.org/10.1287/opre.41.2.269
[20] S. Topaloglu, “A multi-objective programming model for scheduling emergency medicine residents,” Comput. Ind. Eng., vol. 51, no. 3, pp. 375–388, 2006.
[21] S. Kraul, A. Fügener, J. O. Brunner, and M. Blobner, “A robust framework for task-related resident scheduling,” Eur. J. Oper. Res., vol. 276, no. 2, pp. 656–675, 2019. Available: https://opus.bibliothek.uni-augsburg.de/opus4/52399
[22] C.-H. Brech, A. Ernst, and R. Kolisch, “Scheduling medical residents’ training at university hospitals,” Eur. J. Oper. Res., vol. 274, no. 1, pp. 253–266, 2019. doi: 10.1016/j.ejor.2018.04.003
[23] MinSalud, Aproximaciones al Modelo de Relación Docencia Servicio: Modelo de Evaluación de las Prácticas Formativas. [Online]. Available: https://docplayer.es/25096383-Aproximaciones-al-modelo-de-relacion-docencia-servicio-modelo-de-evaluacion-de-las-practicas-formativas.html
[24] HUCSR, “Portafolio de servicios,” 2014. [Online]. Available: http://www.clinicasanrafael.co/hucsr/index.php?option=com_flippingbook&view=book&id=15&page=1&Itemid=260. Accessed on: June 01, 2017.
[25] MinSalud, Manual de acreditación en salud, ambulatorio y hospitalario, Colombia. Bogotá: Ministerio de la Protección Social, 2011. Available: https://www.minsalud.gov.co/sites/rid/Lists/BibliotecaDigital/RIDE/DE/CA/manual-acreditacion-salud-ambulatorio-hospitalario-2011.pdf
Notes
*
Research article
Author notes
a Corresponding author. E-mail: ca.amaya@uniandes.edu.co
Additional information
How to cite this article: Ciro Alberto Amaya-Guio, Lina Patricia Navas-Castaño, and Cesar Humberto Torres-Gonzalez, “Finding installed capacity for practical training in a service at a university hospital,” Ing. Univ., vol. 25, 2021 [Online]. https://doi.org/10.11144/Javeriana.iued25.ficp


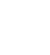

 (1)
(1)

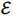


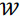
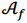
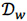
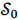
 (2)
(2) (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7)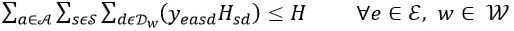 (8)
(8) (9)
(9) (10)
(10) (11)
(11) (12)
(12) (13)
(13) (14)
(14)





