We acknowledge the funding support from Colciencias grant code 120474557650 and the 2019 grant from Faculty of Engineering at Universidad de los Andes, Bogotá, Colombia.
[1] K. Salonitis and P. Ball, “Energy efficient manufacturing from machine tools to manufacturing systems,” Procedia CIRP, vol. 7, pp. 634-639, 2013. https://doi.org/10.1016/j.procir.2013.06.045
[2] W. Li, A. Zein, S. Kara and C. Herrmann, “An investigation into fixed energy consumption of machine tools,” Globalized Solutions for Sustainability in Manufacturing: Proceedings of the 18th CIRP International Conference on Life Cycle Engineering, pp. 268-273, Springer, Berlin, Heidelberg, 2011.
[3] J. R. Duflou, K. Kellens and W. Dewulf, “Unit process impact assessment for discrete part manufacturing: a state of the art,” Journal of Manufacturing Science and Technology, vol. 4, pp. 129-135, 2011. https://doi.org/10.1016/j.cirpj.2011.01.008
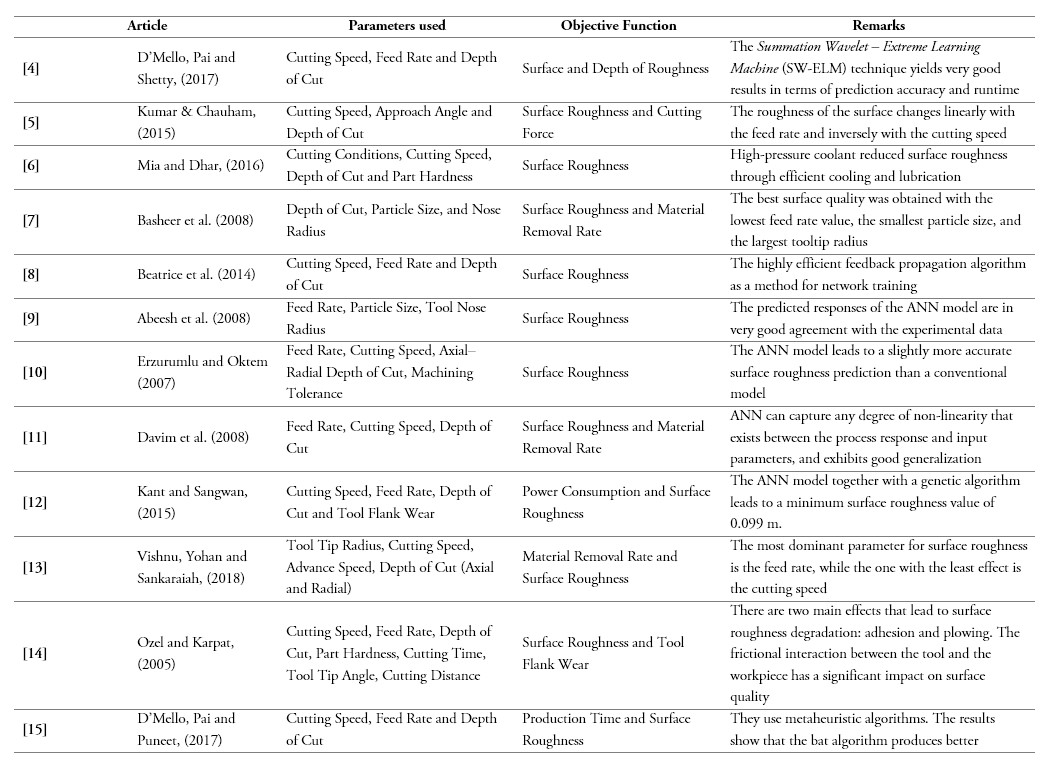
[4] G. D’Mello, P. Srinivasa Pai, and R. P. Shetty, “Surface roughness modeling in high speed turning of Ti-6Al-4V - Artificial Neural Network approach,” Materials Today: Proceedings, vol. 4, no. 8, pp. 7654-7664, 2017. https://doi.org/10.1016/j.matpr.2017.07.099
[5] R. Kumar and S. Chauhan, “Study on surface roughness measurement for turning of Al 7075/10/SiCp and Al 7075 hybrid composites by using response surface methodology (RSM) and artificial neural networking (ANN),” Measurement, vol. 65, pp. 166-180, 2015. https://doi.org/10.1016/j.measurement.2015.01.003
[6] M. Mia and N. R. Dhar, “Prediction of surface roughness in hard turning under high pressure coolant using Artificial Neural Network,” Measurement, vol. 92, pp. 464-474, 2016. https://doi.org/10.1016/j.measurement.2016.06.048
[7] A. C. Basheer, U. A. Dabade, S. S. Joshi, V. V. Bhanuprasad, and V. M. Gadre, “Modeling of surface roughness in precision machining of metal matrix composites using ANN,” Journal of Materials Processing Technology, vol. 197, no. 1-3, pp. 439-444, 2008. https://doi.org/10.1016/j.jmatprotec.2007.04.121
[8] B. Anuja Beatrice, E. Kirubakaran, P. Ranjit Jeba Thangaiah, and K. Leo Dev Wins, “Surface roughness prediction using artificial neural network in hard turning of AISI H13 steel with minimal cutting fluid application,” Procedia Engineering, vol. 97, pp. 205-211, 2014. https://doi.org/10.1016/j.proeng.2014.12.243
[9] B. C. Abeesh, U. A. Dabade, S. S. Joshi, V. V. Bhanuprasad and V. M. Gadre, “Modeling of surface roughness in precision machining of metal matrix composites using ANN,” Journal of Materials Processing Technology, vol. 197, no. 1-3, pp. 439-444, 2008.
[10] T. Erzurumlu and H. Oktem, “Comparison of response surface model with neural network in determining the surface quality of moulded parts,” Materials and Design, vol. 28, pp. 459-465, 2007.
[11] J. P. Davim, V. N. Gaitonde and S. R. Karmik, “Investigations into the effect of cutting conditions on surface roughness in turning of free machining steel by ANN models,” Journal of Material Processing, vol. 205, pp. 16-23, 2008.
[12] G. Kant and K. S. Sangwan, “Predictive modelling and optimization of machining parameters to minimize surface roughness using artificial neural network coupled with genetic algorithm,” Procedia CIRP, vol. 31, pp. 453-458, 2015.
[13] M. V. Vardhan, G. Sankaraiah, and M. Yohan, “Prediction of surface roughness & material removal rate for machining of P20 steel in CNC milling using artificial neural networks,” Materials Today: Proceedings, vol. 5, no. 9, pp. 18376-18382, 2018. https://doi.org/10.1016/j.matpr.2018.06.177
[14] T. Özel and Y. Karpat, “Predictive modeling of surface roughness and tool wear in hard turning using regression and neural networks,” International Journal of Machine Tools and Manufacture, vol. 45, no. 4-5, pp. 467-479, 2005. https://doi.org/10.1016/j.ijmachtools.2004.09.007
[15] G. D’Mello, P. S. Pai, and N. P. Puneet, “Optimization studies in high speed turning of Ti-6Al-4V,” Applied Soft Computing, vol. 51, pp. 105-115, 2017. https://doi.org/10.1016/j.asoc.2016.12.003
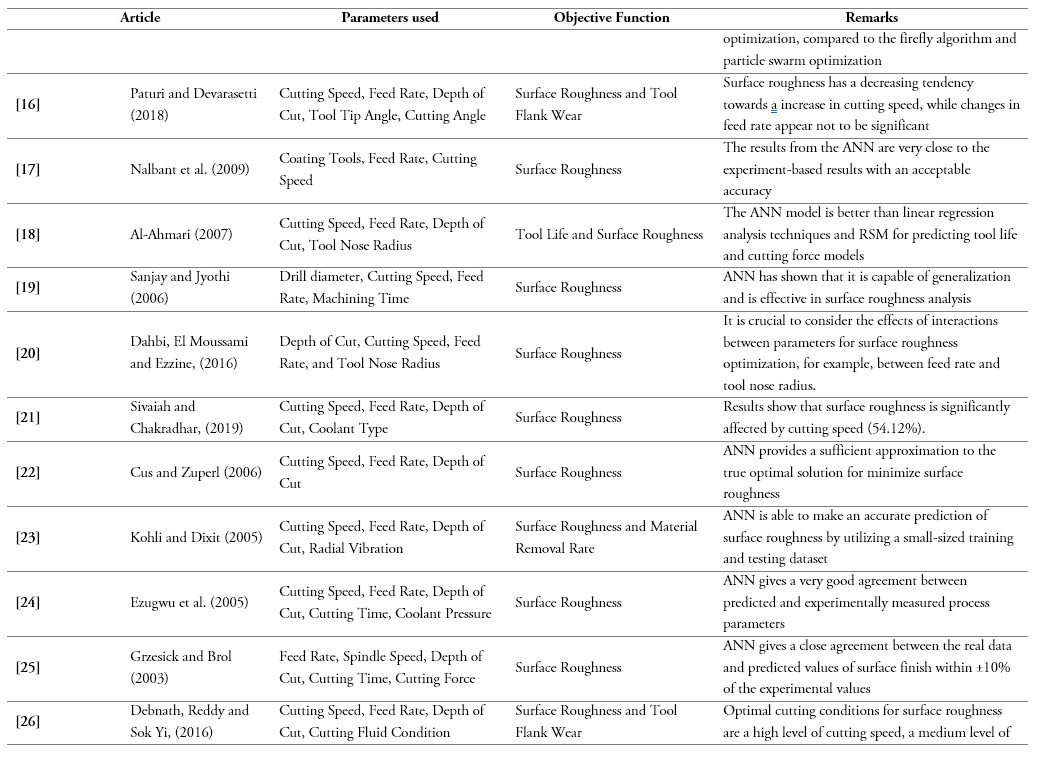
[16] P. Sivaiah and D. Chakradhar, “Modeling and optimization of sustainable manufacturing process in machining of 17-4 PH stainless steel,” Measurement, vol. 134, pp. 142-152, 2019. https://doi.org/10.1016/j.measurement.2018.10.067
[17] M. Nalbant, H. Gokkaya, I. Toktas and G. Sur, “The experimental investigation of the effects of uncoated, PVD and CVD-coated cemented carbide inserts and cutting parameters on surface roughness in CNC turning and its prediction using artificial neural networks,” Robotics and Computer-Integrated Manufacturing, vol. 25, pp. 211-223, 2009.
[18] A. M. A. Al-Ahmari, “Predictive machinability models for a selected hard material in turning operations,” Journal of Materials Processing Technology, vol. 190, pp. 305-311, 2007.
[19] C. Sanjay and C. Jyothi “A study of surface roughness in drilling using mathematical analysis and neural networks,” International Journal of Advanced Manufacturing Technology, vol. 29, pp. 846-852, 2006.
[20] S. Dahbi, H. El Moussami, L. Ezzine, D. Samya, and E. L. M. Haj, “Optimization of turning parameters for surface roughness,” Xème Conférence Internationale: Conception et Production Intégrées, Tanger, Morocco, 2015. https://hal.archives-ouvertes.fr/hal-01260818/
[21] S. Dahbi, H. El Moussami, and L. Ezzine, “Optimization of turning parameters for surface roughness,” International Journal of Modern Engineering Research, vol. 134, pp. 142-152, 2019.
[22] F. Cus and U. Zuperl, “Approach to optimization of cutting conditions by using artificial neural networks,” Journal of Materials Processing Technology, vol. 173, pp. 281-290, 2006.
[23] A. Kohli and U. S. Dixit, “A neural-network-based methodology for the prediction of surface roughness in a turning process,” International Journal of Advanced Manufacturing Technology, vol. 25, pp. 118-129, 2005.
[24] E. O. Ezugwu, D. A. Fadare, J. Bonneya, R. B. D Silva, and W. F. Sales, “Modelling the correlation between cutting and process parameters in high-speed machining of Inconel 718 alloy using an artificial neural network,” International Journal of Machine Tools and Manufacture, vol. 45, pp. 1375-1385, 2005.
[25] W. Grzesick, and S. Brol, “Hybrid approach to surface roughness evaluation in multistage machining processes,” Journal of Material Processing Technology, vol. 134, pp. 265-272, 2003.
[26] S. Debnath, M. M. Reddy, and Q. S. Yi, “Influence of cutting fluid conditions and cutting parameters on surface roughness and tool wear in turning process using Taguchi method,” Measurement, vol. 78, pp. 111-119, 2016.
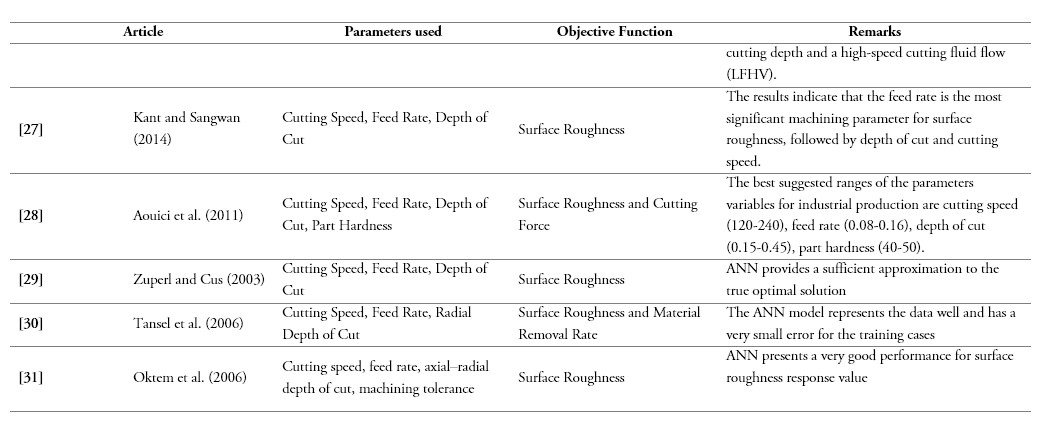
[27] G. Kant and K. S. Sangwan, “Prediction and optimization of machining parameters for minimizing power consumption and surface roughness in machining,” Journal of Cleaner Production, vol. 83, pp. 151-164, 2014.
[28] H. Aouici, M. A. Yallese, K. Chaoui, T. Mabrouki, and J. F. Rigal, “Analysis of surface roughness and cutting force components in hard turning with CBN tool: Prediction model and cutting conditions optimization,” Measurement, vol. 45, no. 3, pp. 344-353, 2012. https://doi.org/10.1016/j.measurement.2011.11.011
[29] U. Zuperl and F. Cus, “Optimization of cutting conditions during cutting by using neural networks,” Robotics and Computer-Integrated Manufacturing, vol. 19, pp. 189-199, 2003.
[30] I. N. Tansel, B. Ozcelik, W. Y. Bao, P. Chen, D. Rincon, and S. Y. Yang, “Selection of optimal cutting conditions by using GONNS,” International Journal of Machine Tools and Manufacture, vol. 46, pp. 26-35, 2006.
[31] H. Oktem, T. Erzurumlu, and F. Erzincanli, “Prediction of minimum surface roughness in end milling mold parts using neutral network and genetic algorithm,” Journal of Material and Design, vol. 27, pp. 735-744, 2006.
[32] G. Kant and K. S. Sangwan, “Prediction and optimization of machining parameters for minimizing power consumption and surface roughness in machining,” Journal of Cleaner Production, vol. 83, pp. 151-164, 2014.
[33] I. Asiltürk and M. Çunkaş, “Modeling and prediction of surface roughness in turning operations using artificial neural network and multiple regression method,” Expert Systems with Applications, vol. 38, no. 5, pp. 5826-5832, 2011.
[34] M. V. Vardhan, G. Sankaraiah, and M. Yohan, “Prediction of surface roughness & material removal rate for machining of P20 steel in CNC milling using artificial neural networks,” Materials Today: Proceedings, vol. 5, no. 9, pp. 18376-18382, 2018.
[35] U. Maheshwera Reddy Paturi, H. Devarasetti, and S. Kumar Reddy Narala, “Application of Regression and Artificial Neural Network Analysis in Modelling of Surface Roughness in Hard Turning of AISI 52100 Steel,” Materials Today: Proceedings, vol. 5, no. 2, pp. 4766-4777, 2018.
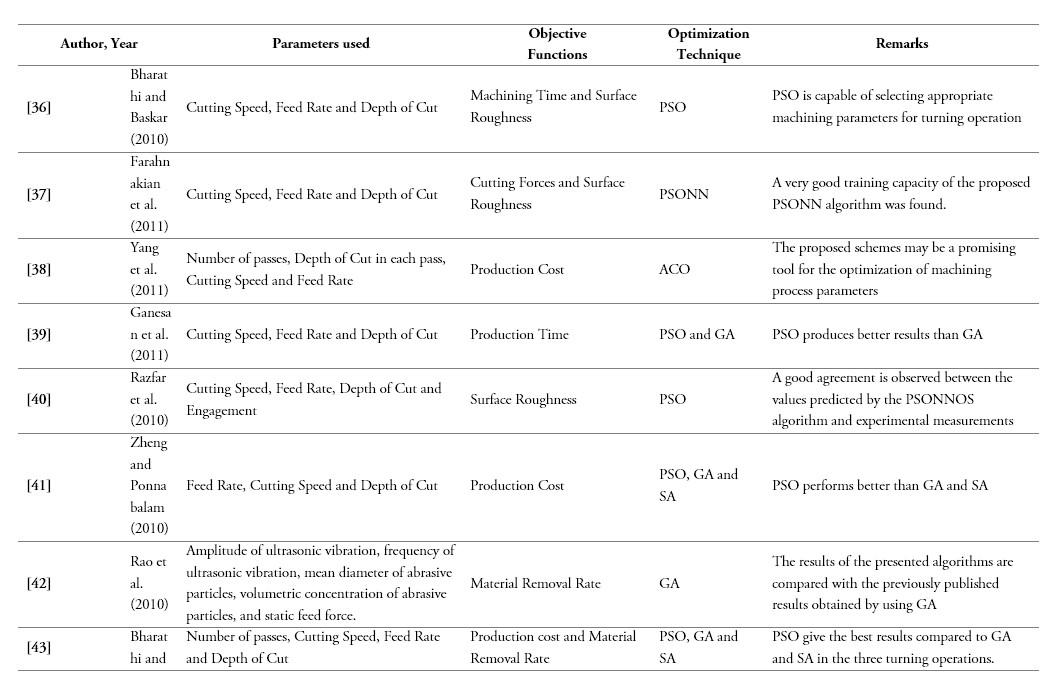
[36] R. S. Bharathi and N. Baskar, “Optimization techniques for machining operations: A retrospective research based on various mathematical models,” International Journal of Advanced Manufacturing Technology, vol. 48, 1075-1090, 2010.
[37] M. Farahnakian, M. R. Razfar, M. Moghri and M. Asadnia, “The selection of milling parameters by the PSO-based neural network modeling method,” International Journal of Advanced Manufacturing Technology, vol. 57, pp. 1-12, 2011.
[38] W. Yang, Y. Guo and W. Liao, “Optimization of multi-pass face milling using a fuzzy particle swarm optimization algorithm,” International Journal of Advanced Manufacturing Technology, vol. 54, pp. 45-57, 2011.
[39] H. Ganesan, G. Mohankumar, K. Ganesan and K. Ramesh Kumar, “Optimization of machining parameters in turning process using genetic algorithm and particle swarm optimization with experimental verfification,” International Journal of Engineering Science and Technology (IJEST), vol. 3, pp. 1091-1102, 2011.
[40] M. R. Razfar, M. Asadnia, M. Haghshenas and M. Farahnakian, “Optimum surface roughness prediction in face milling X20Cr13 using particle swarm optimization algorithm,” Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, vol. 224, no. 11, pp. 1645-1653, 2010. https://doi.org/10.1243/09544054JEM1809
[41] L. Y. Zheng and S. G. Ponnambalam, “Optimization of multipass turning operations using particle swarm optimization”. Paper presented at the ISMA'10 - 7th International Symposium on Mechatronics and its Applications, pp. 1-6, 2010.
[42] R. V. Rao and P. J. Pawar, “Grinding process parameter optimization using non-traditional optimization algorithms,” Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, vol. 224, pp. 887-898, 2010.
[43] R. S. Bharathi and N. Baskar, “Optimization techniques for machining operations: A retrospective research based on various mathematical models,” International Journal of Advanced Manufacturing Technology, vol. 48, pp. 1075-1090, 2010.
[44] J. Xi and G. Liao, “Cutting parameter optimization based on particle swarm optimization,” Paper presented at the 2009 2nd International Conference on Intelligent Computing Technology and Automation, ICICTA, vol. 1, pp. 255-258, 2009.
[45] I. Escamilla, P. Perez, L. Torres, P. Zambrano and B. Gonzalez, “Optimization using neural network modeling and swarm intelligence in the machining of titanium (ti 6al 4v) alloy,” Paper presented at the 8th Mexican International Conference on Artificial Intelligence. Proceedings of the Special Session, MICAI, pp. 33-38, 2009.
[46] J. Ciurana, G. Arias and T. Ozel, “Neural network modeling and particle swarm optimization (PSO) of process parameters in pulsed laser micromachining of hardened AISI H13 steel,” Materials and Manufacturing Processes, vol. 24, pp. 358-368, 2009.
[47] C. Prakasvudhisarn, S. Kunnapapdeelert and P. Yenradee, “Optimal cutting condition determination for desired surface roughness in end milling,” International Journal of Advanced Manufacturing Technology, vol. 41, pp. 440-451, 2009.
[48] J. Srinivas, R. Giri and S. Yang, “Optimization of multi-pass turning using particle swarm intelligence,” International Journal of Advanced Manufacturing Technology, vol. 40, pp. 56-66, 2009.
[49] J. G. Li, Y. X. Yao, D. Gao, C. Q. Liu and Z. J. Yuan, “Cutting parameters optimization by using particle swarm optimization (PSO),” Applied Mechanics and Materials, vols. 10-12, pp. 879-883, 2008.
[50] O. Duran, R. Rodriguez and L. A. Consalter, “PSO for selecting cutting tools geometry,” Lecture Notes in Computer Science, vol. 5271, pp. 265-272, 2008.
[51] Z. Chen and Y. Li, “An improved particle swarm algorithm and its application in grinding process optimization,” Proceedings of the 27th Chinese Control Conference, pp. 2-5, 2008.
[52] H. Zhao, J. G. Li, Y. X. Yao and C. Q. Liu, “Cutting parameters optimization for constant cutting force in milling,” Applied Mechanics and Materials, vol. 483, pp. 10-12, 2008.
[53] H. Liu and W. Huang, “Computer numerical control machining parameter optimization based on particle swarm optimization,” J. of Tongji University, vol. 36, pp. 803-806, 2008.
[54] U. Zuperl, F. Cus and V. Gecevska, “Optimization of the characteristic parameters in milling using the PSO evolution technique,” Journal of Mechanical Engineering, vol. 6, pp. 354-368, 2007.
[55] H. Huang, A. Li and X. Lin, “Application of PSO-based Wavelet Neural Network in Tool Wear Monitoring,” Proceedings of the IEEE International Conference on Automation and Logistics, pp. 2813-2817, 2007.
[56] J. Kennedy and R. C. Eberhart, “Discrete binary version of the particle swarm algorithm,” IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, vol. 5, pp. 4104–4108, 1997. https://doi.org/10.1109/ICSMC.1997.637339
[57] J. G. Li, Y. X. Yao, D. Gao, C. Q. Liu, and Z. J. Yuan, “Cutting parameters optimization by using particle swarm optimization (PSO),” Applied Mechanics and Materials, vols. 10-12, pp. 879-883, 2008. https://doi.org/10.4028/www.scientific.net/AMM.10-12.879
[58] N. Yusup, A. M. Zain, and S. Z. M. Hashim, “Overview of PSO for optimizing process parameters of machining,” Procedia Engineering, vol. 29, pp. 914-923, 2012. https://doi.org/10.1016/j.proeng.2012.01.064
[59] Y. Karpat and T. Özel, “Multi-objective optimization for turning processes using neural network modeling and dynamic-neighborhood particle swarm optimization,” The International Journal of Advanced Manufacturing, vol. 35, no. 3-4, pp. 234-247, 2007.
[60] M. Mia and N. R. Dhar, “Prediction of surface roughness in hard turning under high pressure coolant using Artificial Neural Network,” Measurement, vol. 92, pp. 464–474, 2016. https://doi.org/10.1016/j.measurement.2016.06.048
[61] Ş. Karabulut, “Optimization of surface roughness and cutting force during AA7039/Al2O3 metal matrix composites milling using neural networks and Taguchi method,” Measurement, vol. 66, pp. 139-149, 2015. https://doi.org/10.1016/j.measurement.2015.01.027










 (1)
(1)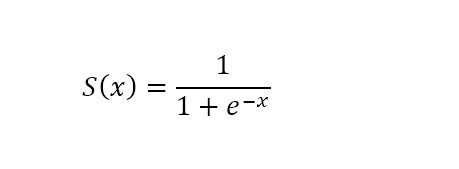 (2)
(2) (3)
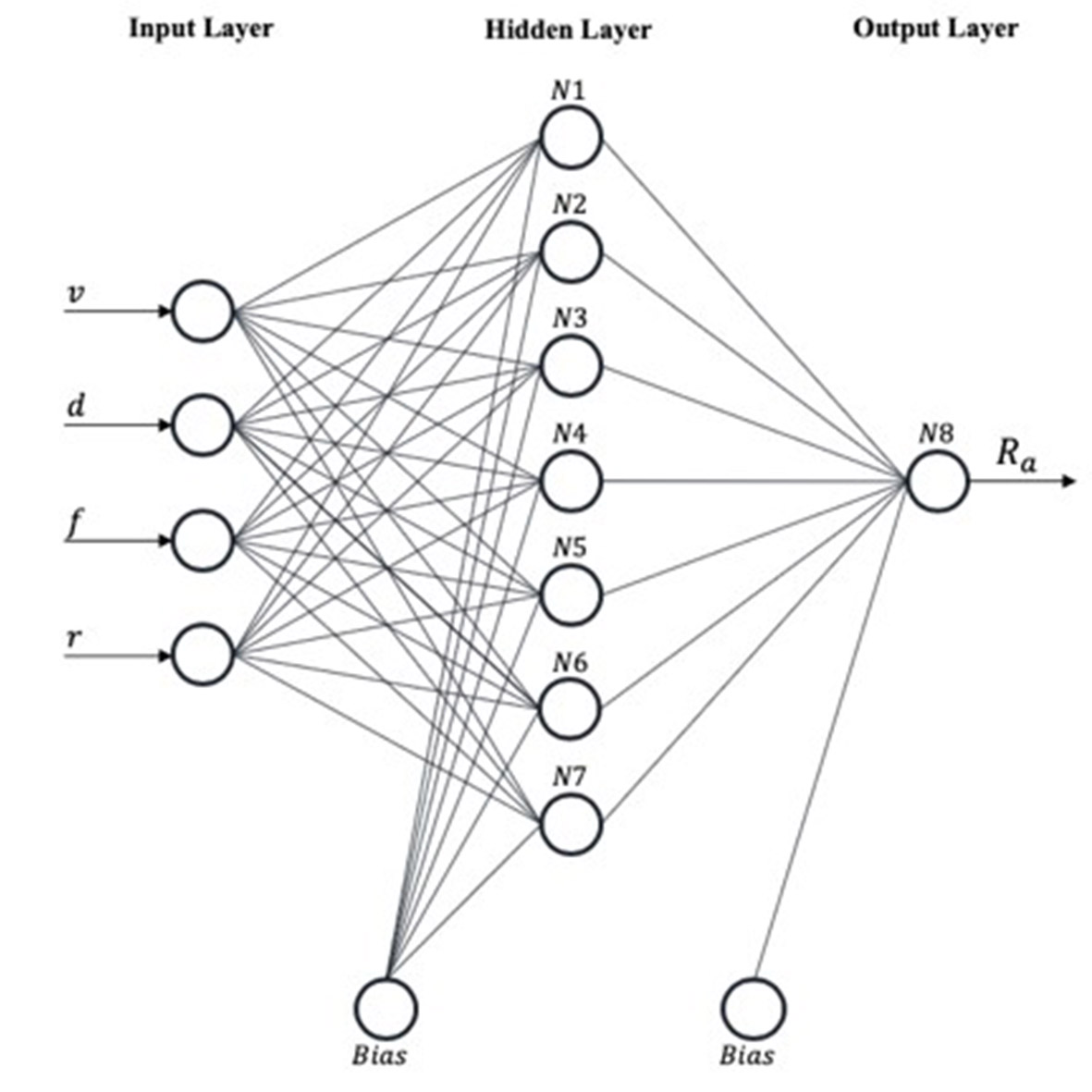
(3)
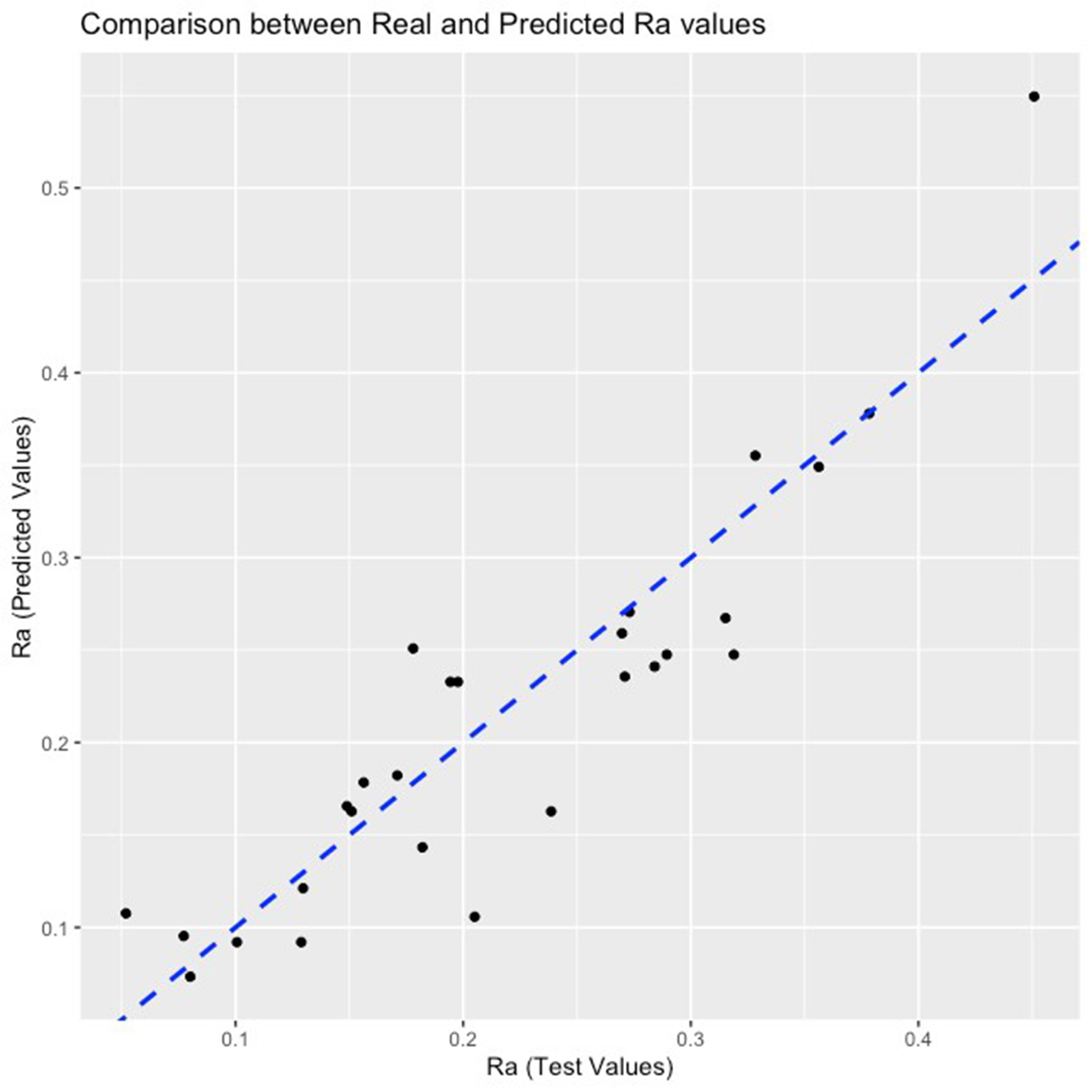
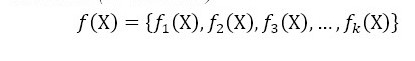 (4)
(4)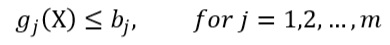 (5)
(5) (6)
(6) (7)
(7) (8)
(8)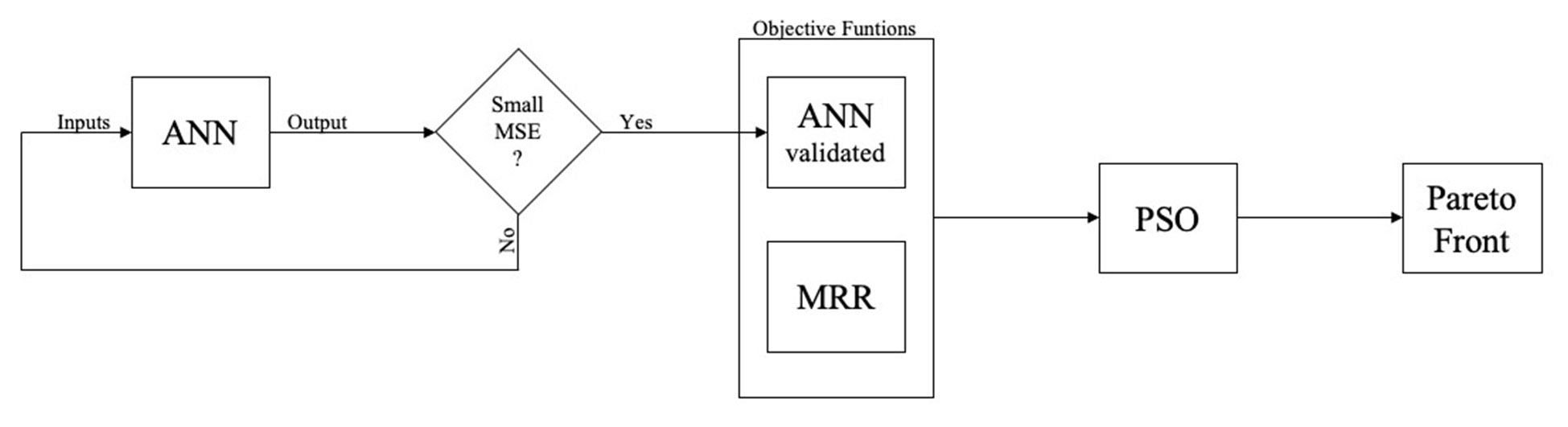
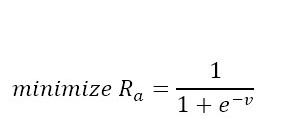 (9)
(9)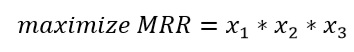 (10)
(10) (11)
(11) (12)
(12) (13)
(13)  (14)
(14)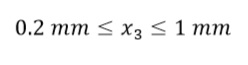 (15)
(15) (16)
(16)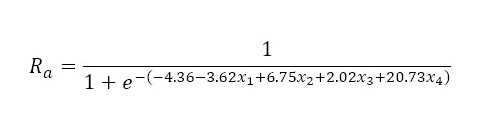 (17)
(17)