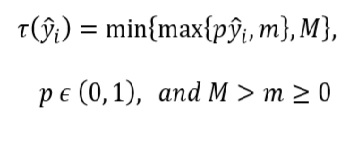Introduction
Social protection in health represents a crucial factor for the progress of any country. It contributes not only to the well-rounded development of citizens at an early age but also to guaranteeing the growth of their economy so that workers enjoy good health, are free of diseases, and do not have physical limitations or a low life expectancy, which could increase labor productivity indexes. Around the world, life expectancy has been improving at a rate of more than 3 years per decade since 1950, except for the 1990s [1]. On the other hand, the demand for surgical services has grown due to two related factors: (i) health care as a universal right, and (ii) the aging of the population [2]. For example, in the European Union, 5647 surgeries per year per 100 thousand inhabitants were reported in 2000; in 2005, the number rose to 5819; and, in 2009, to 6522 [3]. In Colombia, the life expectancy is 77.11 years for women and 70.2 for men [4], and the average waiting time for a surgery after being approved by a doctor is 17.2 days (contributory regimen) [5]. This is not an encouraging panorama; it reveals a growing unmet demand for surgical services approaching in the short or medium term. As a result, health centers should optimize their use of the available resources to meet those needs [2]. The planning and programming of surgical interventions has been a diverse field of knowledge analyzed by multiple researches, because surgery rooms are entities that demand complex logistical interaction and, the Operating Rooms (ORs) represent the highest costs account and source of income in most hospitals [2],[6]. Consequently, the design and implementation of better planning and programming systems is an important tool today, not only to reduce costs but also to improve the access to health services [7].
Several inputs are required to provide solutions for OR scheduling, Operating Room Time (ORT) is one of them [8]. Some authors support the use of uncertainty to estimate surgery duration in this kind of solutions [9]. The duration of a surgery in the OR is highly variable, even in surgeries of the same type. When this variability is positive, it is one of the main causes of surgery rescheduling due to surgical procedures occupy the OR longer than expected [10]. When the variability is negative, it means a low OR utilization rate, i.e., the OR is used less time than expected [11]. Nevertheless, we know ORT is not perfectly predictable; an operation may last longer than expected for various medical reasons [12]. The ORT is conditioned by a set of variables that make OR planning particularly complex. An important step to establish a master surgery program is to classify surgical procedures to reduce the variability and try to homogenize the types of interventions in order to have a more efficient programming and minimize cancellations [13]. Jang et al. (2016) [14] conducted a survey to analyze the current state of OR management and surgical programming in general hospitals in Korea. They concluded that the methods to predict the expected surgical time were decided arbitrarily by surgeons, the experience of the anesthesiologist or based on historical averages. Our case study is conducted at The Hospital San Vicente Fundación (HSVF) in Medellín, Colombia. The HSVF with 662 beds is one of the largest university hospitals in the country. HSVF has 16 ORs and performs more than 20,000 surgical procedures per year, by dealing with different types of surgeries, emergencies, and elective procedures, including transplants. The management of ORs is centralized in a single department to generate greater efficiency in the service. Scheduling of surgeries is done manually by people with clinical knowledge and no training in this type of problem. The accurate allocation of ORT is one of its greatest challenges, currently established by a subjective estimation of surgeons. The HSVF has a cancellation rate of 6% of scheduled surgeries, which in turn affects the generation of idle time. This is a visible problem in the case of the HSVF, which today reports only 67.5% ORs’ occupation.
The main objective of this work is to create a suitable model that can be used to predict ORTs in an intelligence programming system in the HSVF. According to the review of works, this problem has been approached from different perspectives and tools with the use of various data configurations. Normally, the data in this type of studies have complications in their structure, the ORT registered in the information systems correspond to each surgery, and each surgery includes the development of one or more surgical procedures. This makes it impossible to assign a respective ORT for each procedure. Currently, the authors take two paths: (i) eliminating surgeries that contemplate the performance of more than one surgical procedure, e.g. [8], [15], or (ii) assigning ORT only to the main surgical procedure of the surgery, e.g. [16]. Conversely, we use every programed procedure as binary variable to generate surgery distinctions and use interactions among them. In our case about 40% of the records have more than one surgical procedure. In addition, we show the advantage of implementing Latent Class Analysis (LCA) in the construction of a Machine Learning (ML) model by improving the accuracy of predictions and decreasing the bias of error distribution. We hypothesize that a clustering strategy of procedures and others surgery characteristics would increase accuracy and model adjustment. Additionally, these cluster variables could be utilized to get a more parsimonious model with a smaller data dimension. Considering the good performance of ML models in estimating ORT [17], we evaluate three tree-based models and tested different data-set configurations of predictors to find a more parsimonious model. The tree models are the Classification and Regression Trees model (CART), and two ensemble models: Conditional Random Forest (CFOREST) and Gradient Boosting Machine (GBM).
This paper is organized in different sections. In section 2, we review studies with a similar scope in advanced techniques for data analysis published in the last decade. In section 3, we describe the database used for research and statistical treatments. In the same section, we detail the assembly, clustering, and evaluation methods adopted in this work. In section 4, we present the results and analysis of these. Finally, conclusions and future works are discussed in section 5.
Literature review
The prediction of the ORT has been a challenge that many researchers have analyzed from different perspectives. Based on regression models and hypothesis testing, Kays et al. [18] used bias and mean absolute deviation to evaluate the performance of the methods of estimation of ORTs. They concluded that, although it is possible to improve the estimates of surgery duration, the inherent variability in these estimates remains high; therefore, it is necessary to be careful when they are used to optimize OR programming. Stepaniak et al. (2010) [19] analyzed the duration times of surgeries using an ANOVA model. They concluded that, when the factors of the surgeon are incorporated, the accuracy of the prediction of the duration of surgery is improved by more than 15 percent compared to current planning procedures. Shahabikargar et al. (2017) [8] used predictive models that include linear regression (LR), multivariate adaptive regression splines (MARS) and random forest (RF) to predict the time of the procedure of elective surgeries. They found that the random forest model outperformed other models and produced an improvement of 28% compared to the current method employed at the hospital. Eijkemans et al. (2010) [16] analyzed the data of the total time of the ORs with a mixed linear model. They showed that, by using a prediction model instead of the surgeon's prediction based on historical averages, the shortest expected duration would be reduced by 12%, and the longest expected duration, by 25%. In addition, Wu (2017) [20] compared the performance of a surgeon's prediction with a method potentially more accurate than using historical averages. They utilized Kruskal-Wallis variance analysis and Steel-Dwass pairwise comparisons to calculate the duration of primary total knee arthroplasty (TKA) procedures. They concluded that none of the historical estimates were significantly different from each other, demonstrating a lack of improvement in presence of additional cases, and that even a small number of cases can reduce estimation biases compared to the exclusive use of surgeons' estimates.
Likewise, other researchers tried to improve estimates using new strategies or combinations of existing ones. The literature includes the work of Lorenzi et al. (2017) [21], who used hierarchical predictive clustering (PHC) to group procedures based on current procedural terminology (CPT) codes. They showed that PHC improves specific patient outcomes compared to the clusters currently used according to clinical criteria. Spangenberg et al. (2017) [22] used big data architecture for integrated processing of real-time and historical data about common surgical events to create prediction models. They showed that the model is competitive in terms of the accuracy of the prediction. ShahabiKargar et al. (2017) [8] extend their previous work to the use of assembly algorithms based on decision trees (M5, LSBoost and Bagging Tree), showing that the LSBoost and Bagging Tree models have a better performance in relation to the random forest with a reduction in the MAPE (Mean Absolute Percentage Error) from 38% to 31%. Recently, Tuwatananurak et al. (2019) [23] developed a proprietary machine learning engine which evaluates various models such as gradient-boosted, decision trees and random forests. Although the authors did not indicate the best model structure, they point out the outperform of the machine learning approach respect to average historical means for case duration used by the hospital. Bartek et al. (2019) [24] showed again the highest predictive capability of machine learning model respect to subjective surgeon estimates. Excluding surgeons with less than 100 historical procedures and taking only the primary surgery procedure, they generated a series of XGBoost (Extreme Gradient Boosting) specific models at the surgeon and specialty level. They found that modeling at surgeon-specific level rather than specialty-specific increases the accuracy of the prediction.
Materials and methods
Data set
In this study, we used data from the HSVF with a focus on elective surgeries to model the current operation of ORs. We considered the surgeries performed in 2017 with the aim of avoiding operational and technological changes introduced previously. The initial data set is composed of 2851 cases of priority and non-urgent surgeries. From this set, we eliminated 34 inconsistent cases, with negative times, zero times, or with a surgery time greater than the operating room time. Additionally, we concentrated on the main specialties with at least 100 cases, resulting in a final data set with 2220 cases. In the first column of table 1, we present the predictors we used in the study: patient characteristics, operation characteristics and medical team characteristics. The second column contains the description of each predictor. Finally, third column presents a statistical summary, including the average, maximum and minimum values for the numerical variables and the percentage for the binary variables.
From table 1, we can observe (in Patient characteristics) that most patients were men (67.4%), and the average time elapsed from the approval to the surgery was 24.18 days. Regarding Operation characteristics, the most common medical specialties of the surgeries were orthopedics and traumatology (44.10%). General anesthesia was the most used (72.61%) and OR3 (14.55%) was the OR with the highest number of surgeries scheduled. Surgeries are scheduled primarily between Tuesday and Friday, with a similar number of surgeries between the morning and afternoon hours. Finally, Medical team characteristics shows the number of previous operations performed by the surgeon (50.9) compared to the number of previous operations performed by the anesthesiologist (11.9).
To explore the potential influence of different variables on ORT, figure 1 shows the bivariate plots of the relationships between predictors and ORTs. We can observe that the distribution of ORTs in most plots is asymmetric to the right, where 81% of the surgeries last less than 200 minutes (3.33 hours) and the longest procedures take 820 minutes (13.66 hours), which is similar to the lognormal distribution reported in another work [15]. Turning now to Patient characteristics, no important differences in time with respect to sex are observed, and there is a weak tendency of ORT to growth as age increases. Operation characteristics presents surgeries with different time distributions, some with less bias; for example, orthopedics and traumatology, along with pediatrics, exhibit the highest average times. We can also observe that surgery duration increases as the number of types of anesthesia and procedures grows. In turn, surgery duration in different ORs can be longer or shorter; for example, rooms 3, 5, 8, 9 and 14 exhibit the longest times. The experience of the surgeon is measured as the number of previous operations performed and, as it increases, surgery duration decreases. A similar behavior can be seen about anesthesiologists, with no significant impact.
Table 1
Statistical summary of the predictors
Source: Own elaboration
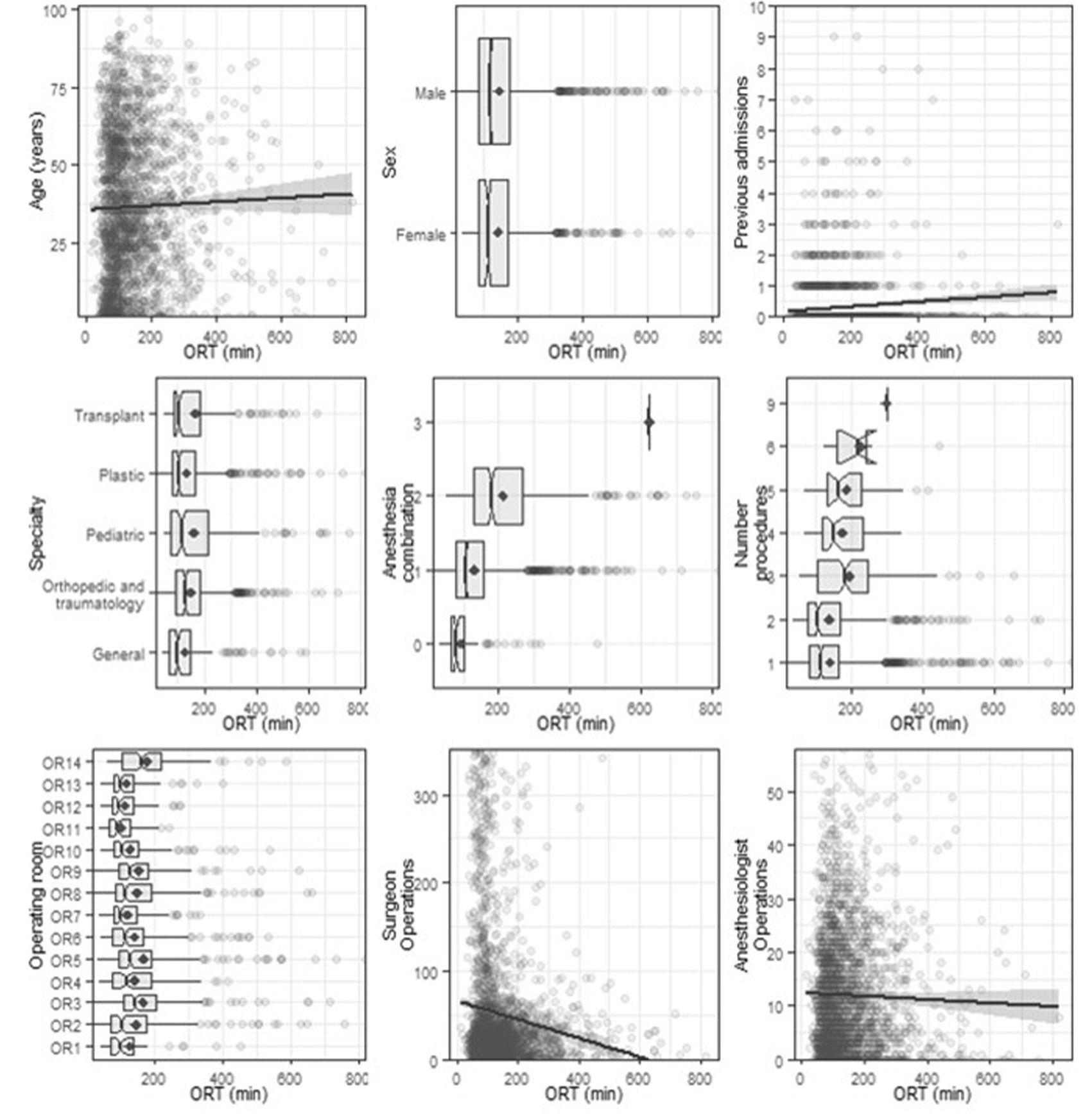 Figure 1
Bivariate plots of relationships between individual predictors and ORT in minutes
Figure 1
Bivariate plots of relationships between individual predictors and ORT in minutes
Source: Own elaboration
LCA to cluster surgical procedures
We used the list of procedures that were defined for a surgery to find subgroups and obtain additional information about the type of surgery being performed. For this purpose, we used Latent Class Analysis (LCA), a clustering-based method that allows the identification of latent structures underling a set of manifest variables [25]. Let 𝐿 be this latent variable with 𝑐 = 1,...,𝐶 latent classes (subgroups) and 𝑌𝑗 one of the 𝑀 manifest variables. Then 𝑃(𝑌𝑗 = 𝑦𝑗|𝐿 = 𝑐) is the conditional probability of observing the response 𝑦𝑗 in the variable 𝑌𝑗 given membership in class 𝑐. These conditional probabilities are used to interpret classes based on the profile of each manifest variable. 𝑃(𝐿 =
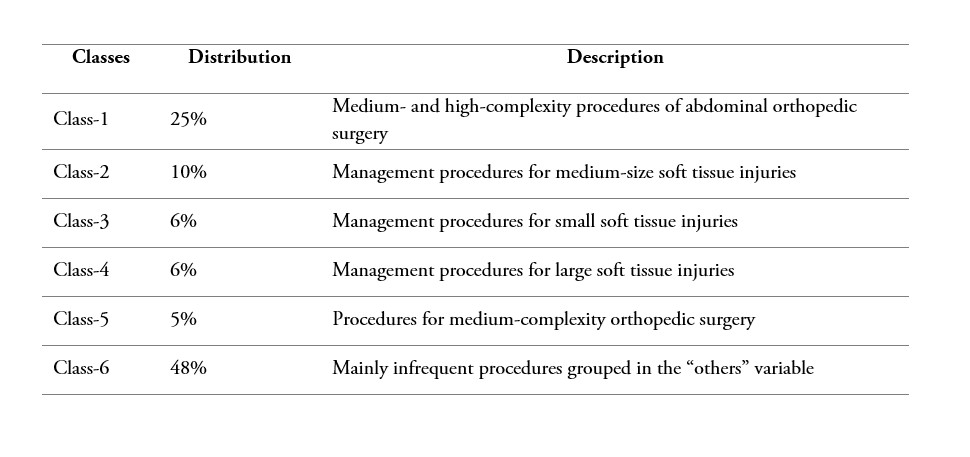
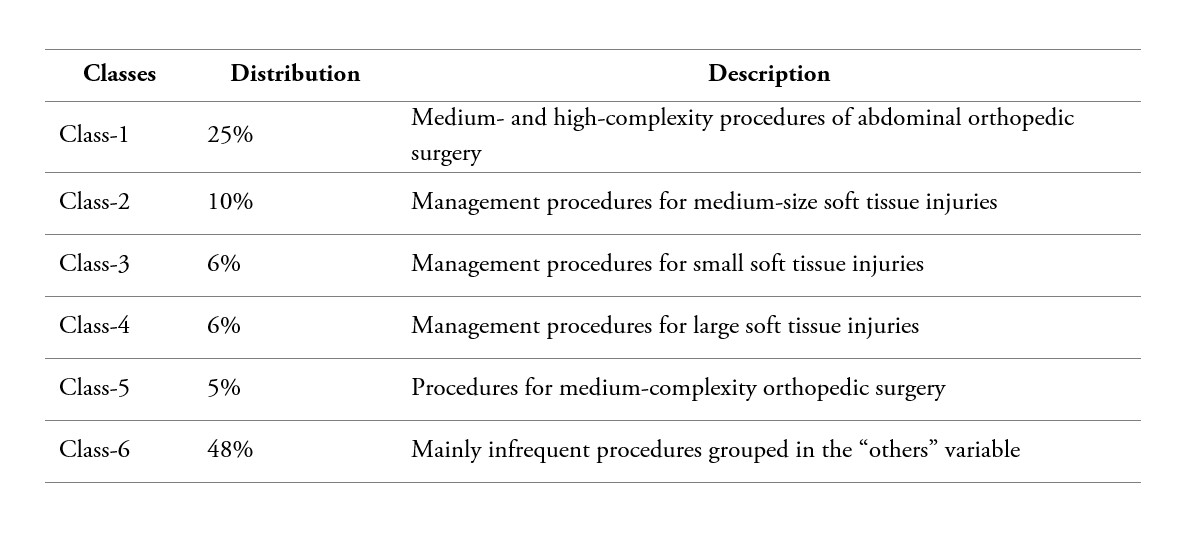
For this application, we have 150 indicator variables; they correspond to each one of planned procedures that can be performed in a surgery. However, with the aim of reducing sparseness, we selected the procedures with a frequency of at least 40 observations; thus, obtaining a filter set of 20 indicator variables. The other less frequent procedures were combined into one indicator called “others”, for a final set of 21 indicator variables. The latent class model was fitted using the R add-on package poLCA [28], and the optimal number of classes was selected based on Bayesian Information Criterion (BIC). As a result, a model with 6 classes, the one with the lowest BIC, was obtained. Additionally, considering the effect on goodness-of–fit tests of sparse contingency tables [27]-[29], we used a bootstrap analysis to estimate the goodness-of-fit test. We obtained a p-value=0.663 for a chi-square test, which indicates a good fit of the model. The estimated distribution of surgery subgroups of similar procedures is described in table 2.
Table 2
Latent Class distribution of surgical procedures
Source: Own elaboration
Creating the clustering variable
Since our main goal is to obtain good predictions of ORT, we tested the implementation of a clustering strategy to establish if it would improve prediction accuracy by finding subgroups of similar operations [30]. To define this new variable, we used patient characteristics (age, sex, previous admissions, and elapsed time since approval), operation characteristics (specialty, anesthesiology indicators, number of procedures, and OR), and medical team characteristics (surgeon and anesthesiologist experience).
Because we have numerical and nominal variables in the data set, it is necessary to use an appropriated method to measure the dissimilarity between any pair of operations considering mixed variable types. Gower coefficient is a dissimilarity measurement that can be used in such cases of mixed type variables and, as indicated in equation Error! Reference source not found.), it is based on a mean weight of dissimilarities between each pair of variables, where 𝑤𝑘 is the weight or contribution of variable 𝑘;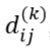 , a value between [0.1] measuring the dissimilarity between subjects (𝑖,𝑗) on variable 𝑘; and 𝑝, the number of variables in the data set [31]-[34].
, a value between [0.1] measuring the dissimilarity between subjects (𝑖,𝑗) on variable 𝑘; and 𝑝, the number of variables in the data set [31]-[34].
The calculation of 𝑑𝑖𝑗(𝑘) will depend on the type of variable, as follows [34]:
-
For nominal and binary variables, 𝑑𝑖𝑗(𝑘) takes a value 0 if the rows (𝑖,𝑗) are equal on variable 𝑘, and 1 in the contrary case.
-
When the variable 𝑘 is continuous, it takes the absolute difference of both values over the full range of the variable 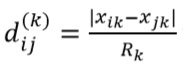 where 𝑅𝑘 = max(𝑥𝑘) − min (𝑥𝐾), is the full range of variable 𝑘.
where 𝑅𝑘 = max(𝑥𝑘) − min (𝑥𝐾), is the full range of variable 𝑘.
-
For ordinal variables, a codification 1:𝑀 of the levels of the variable is carried out, where 𝑀 is the number of levels. The standardization for continuous is subsequently applied.
Applying the previous process and assigning the same weights to the surgery variables, we obtain dissimilarity measurements 𝑑(𝑖,𝑗) between [0.1], where values near 0 mean more similarity, and near 1, more difference. After a dissimilarity measurement was obtained for each pair of rows, we applied two different clustering methods, one partitional and one hierarchical. For partition, we have the k-medoid, which is a centroid-based method where the center of each cluster corresponds to one observation of the cluster and the method is generalized to arbitrary dissimilarities, contrary to k-means, which requires quantitative variables [32]. In the hierarchical method, we used agglomerative hierarchical clustering with an average link metric that generates a bottom-up grouping strategy, where initially each object forms its own cluster and they are sequentially grouped with each other until all the objects belong to a single large cluster [32], [33]. These methods are applied using the PAM (Partitioning Around Medoids) and AGNES (Agglomerate Nesting) algorithms available in the clustering package in R [34].
To evaluate surgery clustering performance and select the best cluster, we used the silhouette coefficient which evaluates the quality of the clusters by verifying their compactness and connectivity [35]. The Silhouette criteria 𝑠(𝑖) is a measurement between 1 and -1 that evaluates the internal consistency of the clusters by comparing the current group assignment of subject (𝑖) with the next best group assignment; values near 1 mean a good current assignment [36]. See equation (3):
where 𝑎(𝑖) is the average distance between subject (𝑖) and the other members of the current group and 𝑏(𝑖) is the shortest average distance to the other groups where it does not belong to, i.e., 𝑏(𝑖) would be the next best group membership. Thus, to obtain a 𝑠(𝑖) near 1, is necessary that 𝑎(𝑖) << 𝑏(𝑖), it means that the distance to the members of the current group is less than the distance to the members of the next best group [36].
The clustering analysis can be seen in figure 2, where different number of clusters are assessed. The graphs show that, in general, the hierarchical method provides better results than PAM clustering. It can be observed that the best Silhouette value for the hierarchical method is achieved when we have 37 clusters. The PAM method presents more unstable Silhouette values, and it tends to generate a similar number of observations per cluster, contrary to the hierarchical method, where there is a higher variance in the number of observations per cluster, discarding outliers and including clusters with 1 and 4 observations.
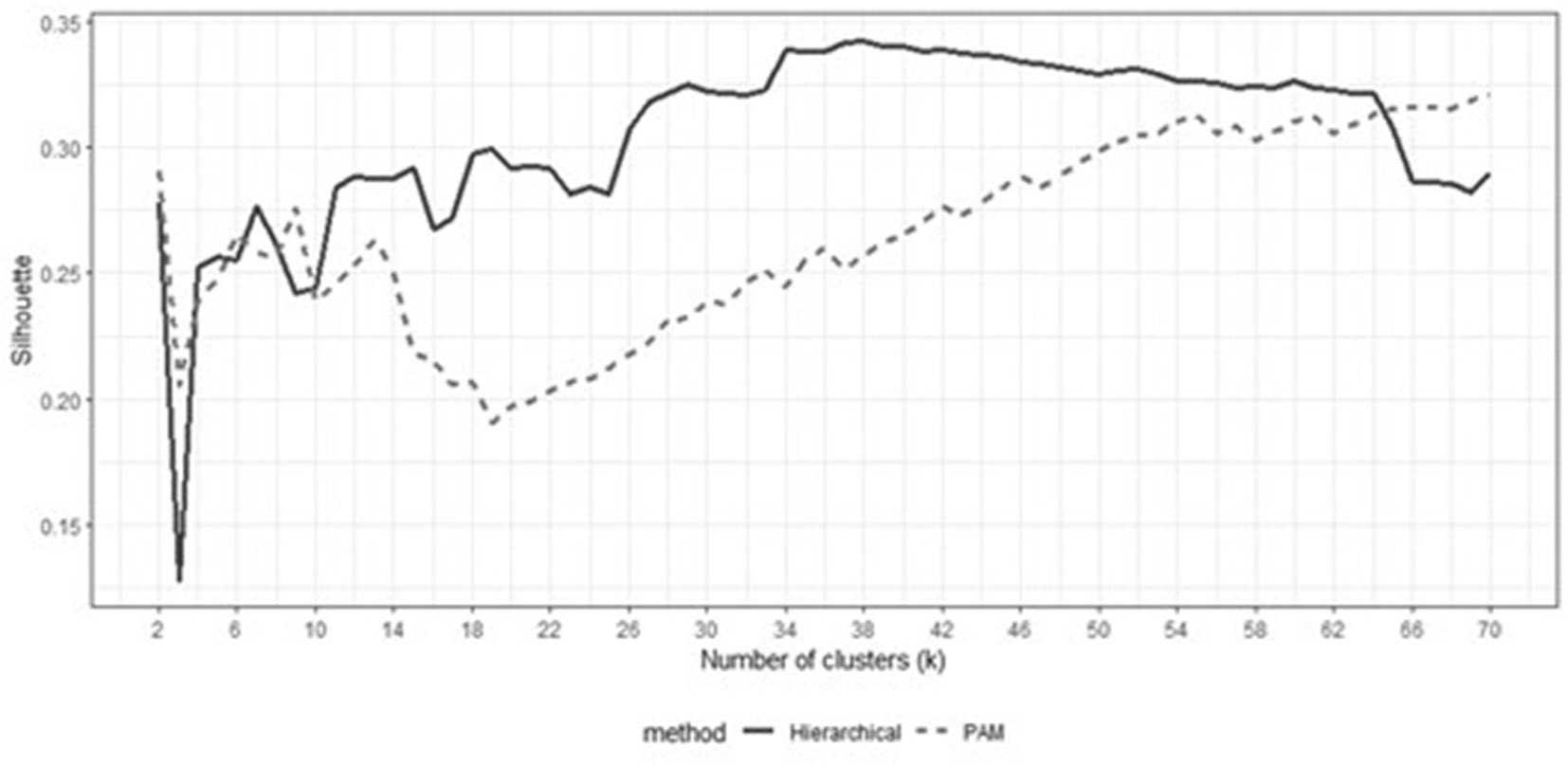 Figure 2
Behavior of the Silhouette coefficient for different numbers of clusters for hierarchical and PAM clustering methods
Figure 2
Behavior of the Silhouette coefficient for different numbers of clusters for hierarchical and PAM clustering methods
Source: Own elaboration
Predictions models
For the prediction of the ORT, we used tree-based methods, which offer the advantage of being able to handle nonlinear relationships; moreover, they identify complex interactions among predict variables and do not require prior data transformation. The first model is CART (Classification and Regression Trees), used as the base model to evaluate the improvement of the other models and implemented in the R add-on package rpart [37]. The other models applied in this work are the ensemble methods Random Forest and Gradient Boosting Machine (GBM), which use trees as base learners. For Random Forest, we used Conditional Random Forest (CFOREST) which, contrary to the algorithm proposed by Breiman (2001) [38], uses conditional inference trees as base learners that perform unbiased recursive partitioning and statistical testing for evaluating the significance of a split decision [39]-[41]. That model is implemented in the CFOREST function that CTREE uses to fit a conditional tree in each bootstrap sample; both functions are in the R add-on package [40]. CFOREST can also be used to evaluate variable importance in prediction accuracy, and it is different from Random Forest, which is biased to select variables with more categories as the most important. CFOREST is more reliable to identify the most relevant variables when it is used together with sampling without replacement [41]. For the third model, we used a boosting approach, where weak learners are added successively so that the new learner focuses on the subjects that were difficult to predict for the previous learners to finally get a stronger combined model. Likewise, Friedman (2001) [42] presented the Gradient Boosting Machine (GBM), a general framework for boosting models where decision trees, as base learners, are added iteratively so that each additional tree reduces a lost function; in this regression case, the squared error. The GBM model here was fitted using R's add-on package gbm [43]. By the other hand, to have a more symmetric response distribution, we decided to build the prediction models with the logarithm of the total ORT [15], then the final prediction is obtained by applying an exponential transformation on the estimation of each model.
Model evaluation
To evaluate the performance of the prediction models, and considering the small data set at hand, we first divided the data between the training set and the test set with a proportion of 90%-10% respectively. In the training set, we used a ten-fold cross-validation to tune and train the model. The test set was used only to estimate the final accuracy measurement. The accuracy measurements employed in this work to compare the models are Root Mean Square Error (RMSE), Mean Absolute Error (MAE) and Operational Accuracy metric developed by Master et al. [44]. Additionally, we also investigated if the models tend to systematically overestimate or underestimate ORTs. RMSE (equation 5) and MAE (equation 6) measure the error distance between the real value 𝑦𝑖 and the predicted value 𝑦 ̂𝑖 without considering if the error direction is positive or negative, and especially RMSE penalizes large errors. Particularly, we used the RMSE to train the models in this work. Although these metrics are statistically meaningful, we used the Operational Accuracy metric (equation 6 ) that gives us a measure of accuracy that can be operationally meaningful to hospital providers [45]. A prediction is "correct" if the absolute value of the error is less than a percentage tolerance of the prediction of 𝑌 ̂, defined as 𝜏(𝑌 ̂) [44]. But this percentage must be within the limits [𝑚,𝑀], which represent the allowed deviation boundaries for short and long OR times, respectively. For our case and in agreement with an expert of the hospital we set 𝑝 = 30%,𝑚 = 15 𝑚𝑖𝑛𝑢𝑡𝑒𝑠,𝑀 = 60 𝑚𝑖𝑛𝑢𝑡𝑒𝑠. This means that for operations that may take a long time (e.g. 6 hours), an error of up to 60 minutes is permissible. If it deviates more than this time, it is considered incorrect.
Where:
On the other hand, table 3 shows the four different data sets defined in this study to test the accuracy improvement of the variables created through the clustering methods described previously.
Table 3
Data sets considered for prediction modeling

Source: Own elaboration
A parameter tuning of the models was carried out with R's add-on package caret [46], thus obtaining the optimal accuracy parameter configuration for each model. Using the Basic data set, for the CART model, we calculated a complexity parameter = 0.0099; for CFOREST, a number of trees = 300 and the number of candidate variables at each node = 100%; and in the GBM model, number of trees = 200, maximum depth of each tree = 5, minimum number of observations in terminal nodes = 5, and learning rate or shrinkage = 0.1. For the Full data set, we estimated a different configuration for each model: CART, complexity parameter = 0.0024; CFOREST, number of trees=500 and the number of candidate variables at each node = 100%; and GBM, number of trees = 300, maximum depth = 5, minimum number of observations = 5, and learning rate = 0.1.
Results
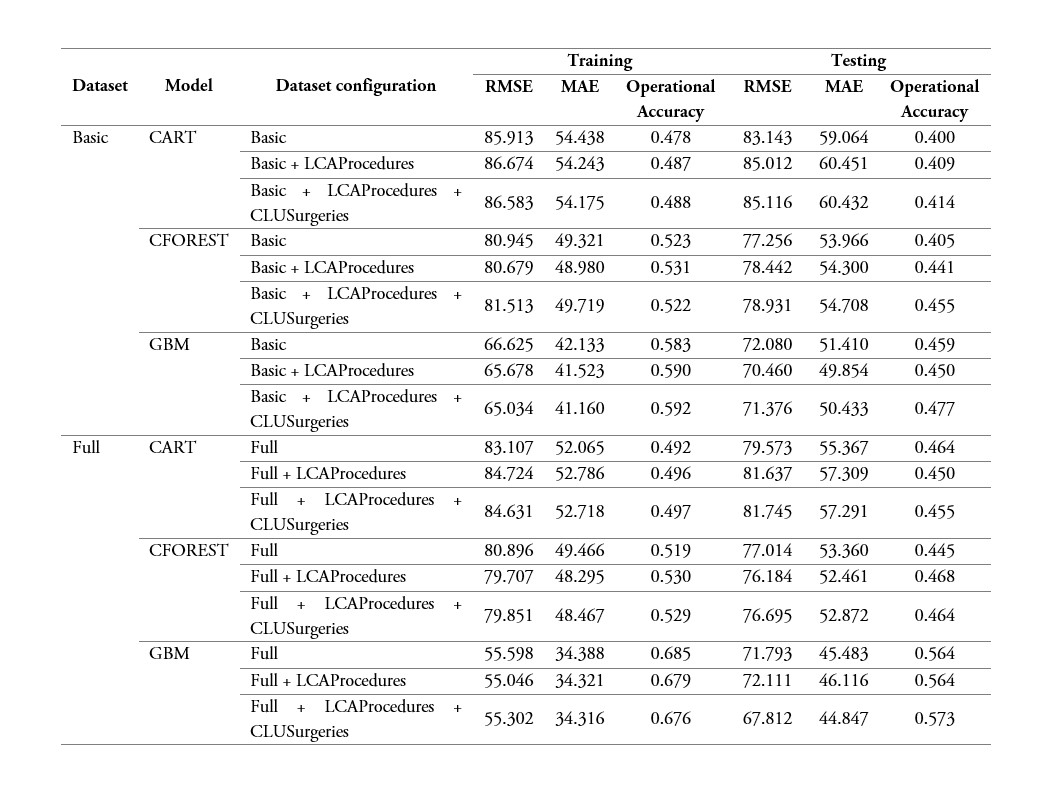
The resulting prediction models for training and testing sets are presented in table 4. As expected, we observed a reduction in the accuracy of the test set with respect to the training set. While for the best model in the training set, we obtained MAE=34.31 minutes and an operational accuracy of 68.5%, in the test set, the metrics were reduced to 44.84 minutes and 57.3% respectively. Considering only the test results, we can see that by adding the variables LCAProcedures + CLUSurgeries there is an average increase in the operational accuracy of about 4%. This change is greater in the basic data set. However, when observing the RMSE and MAE metrics, an average decrease of -0.06% and -0.49% respectively is observed. This behavior, on the other hand, when including the new variables, is not uniform in all models: the Full GBM model presents a 6% improvement in the RMSE; the Full CFOREST model worsens by -3% in the same indicator; the Basic CFOREST model shows a 12% improvement in its operational accuracy. In general, the GBM model shows an improvement by including the variables.
Regarding the models, we can see that GBM produced the lowest RMSE and MAE values and the highest operational accuracy. In the Full scenario, GBM shows more than 10% improvement in operational accuracy over the other models. In the Basic scenario, CFOREST and GBM show a similar performance; however, GBM is superior. CART presents the worst results under all the scenarios described in this study because the assembly feature the other models have given them an advantage to improve their accuracy. In the second part of table 4, we have the accuracy measurements for the three models using the Full data set, which comprises initially 166 predictors, including the 150 indicator variables related to all the procedures. Overall, we observed an average improvement of 13.58% in operational accuracy and 6% in MAE, when moving from the basic to the full data set.
Table 4
Accuracy results for the models CART, CFOREST and GBM with the Basic and Full data sets and the new artificial variables
Source: Own elaboration
Taking the prediction models with the data set that produces the lowest accuracy measurement, we also investigated their tendency to overestimate or underestimate the ORT. figure 3 shows the distribution of the raw errors 𝑦𝑖 − 𝑦 ̂𝑖 for the selected models together with the estimated error mean and skewness of the distribution. The GBM model with the Full + LCAProcedures + CLUSurgeries data set presents the most symmetric distribution of errors, while the CFOREST models tend to produce more skewed distributions to the right, which means a lower capacity to predict high ORTs. The accurate prediction of high ORTs is a challenge for all the models since, as it can be seen, all the distributions show heavier tails on the right. This indicates that all the models tend to underestimate the actual ORTs of atypical procedures that can take up to 13.67 hours. This possible difficulty was considered since the beginning of this work; however, we decided not to discard these extreme times since they are part of the operating reality of ORs. In general, the Full scenario with the GBM model generates the most symmetrical error distributions. All these results indicate that the most appropriate model for the prediction of ORTs is GBM with the complete set of predictors (Full) and the new variables obtained through the LCA of the indicator variables of surgical procedures and the cluster of surgeries.
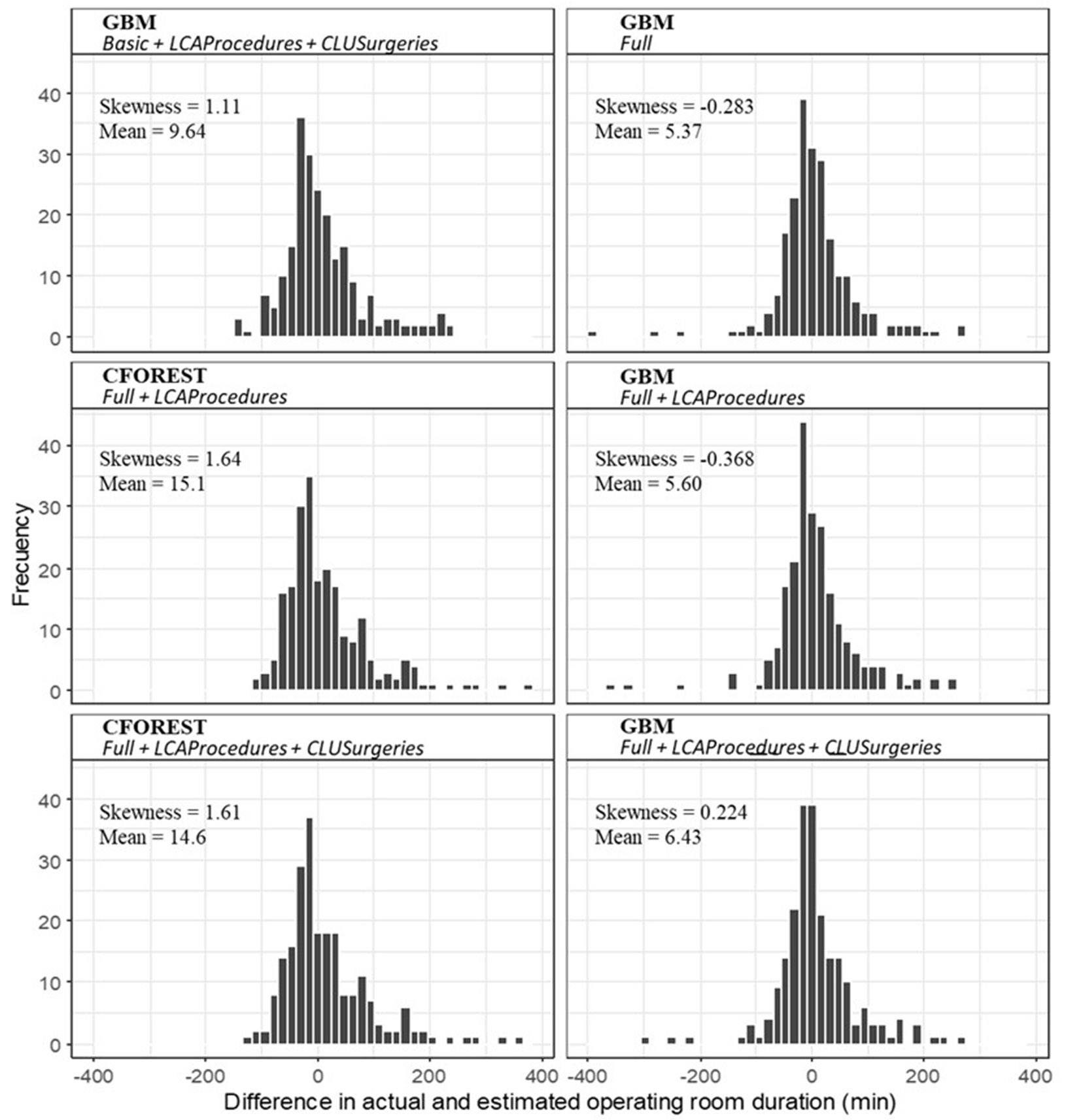 Figure 3
Error distribution of the operating room time predictions of the best models
Figure 3
Error distribution of the operating room time predictions of the best models
Source: Own elaboration
CFOREST and GBM also define the importance or contribution of each variable for ORT prediction. table 5 shows the first 15 variables that contribute most to the prediction of each model. The CFOREST model with Full + LCAProcedures + CLUSurgeries provided competitive results under the scenario with basic predictors, and the GBM model with Full + LCAProcedures + CLUSurgeries produced the best results. The CFOREST model, as previously mentioned, under sampling without replacement and using conditional trees, generates an unbiased evaluation of variable importance. The method in this case consists in computing the measurement Mean Decreased Accuracy, which is obtained by permuting each variable and collecting the reduction in the prediction error on the out-of-bag (OOB) portion of data that was not used for fitting a tree and then average over all trees [40], [41]. In the GBM model, this describes the Relative Influence of each variable on the reduction of the lost function which, in this case, is measured as the reduction in the squared error obtained from every time the variable was selected for splitting and then average over all trees [42], [43]. For both models, the measure of importance was scaled to the sum of 100. Although the rank of importance varies from model to model, we can see that the variables: Surgeon, Number of procedures, Operation Room, LCAProcedures, CLUSurgeries and some specific procedures. The surgeon's experience, measured as the number of previous operations performed, is also an important factor, although it is not in the top positions, both models rank it among the first 15. Additionally, anesthesia combination and anesthesia with assisted sedation are identified by the CFOREST model. The fact that the variables LCAProcedures, CLUSurgeries are in the first positions could mean that the structure and subgroups that are found by means of latent classes analysis and the hierarchical method, are not directly detected by the prediction models.
Table 5
Variable importance ranking form most to least significant for CFOREST and GBM models with Basic and Full datasets of predictors, respectively
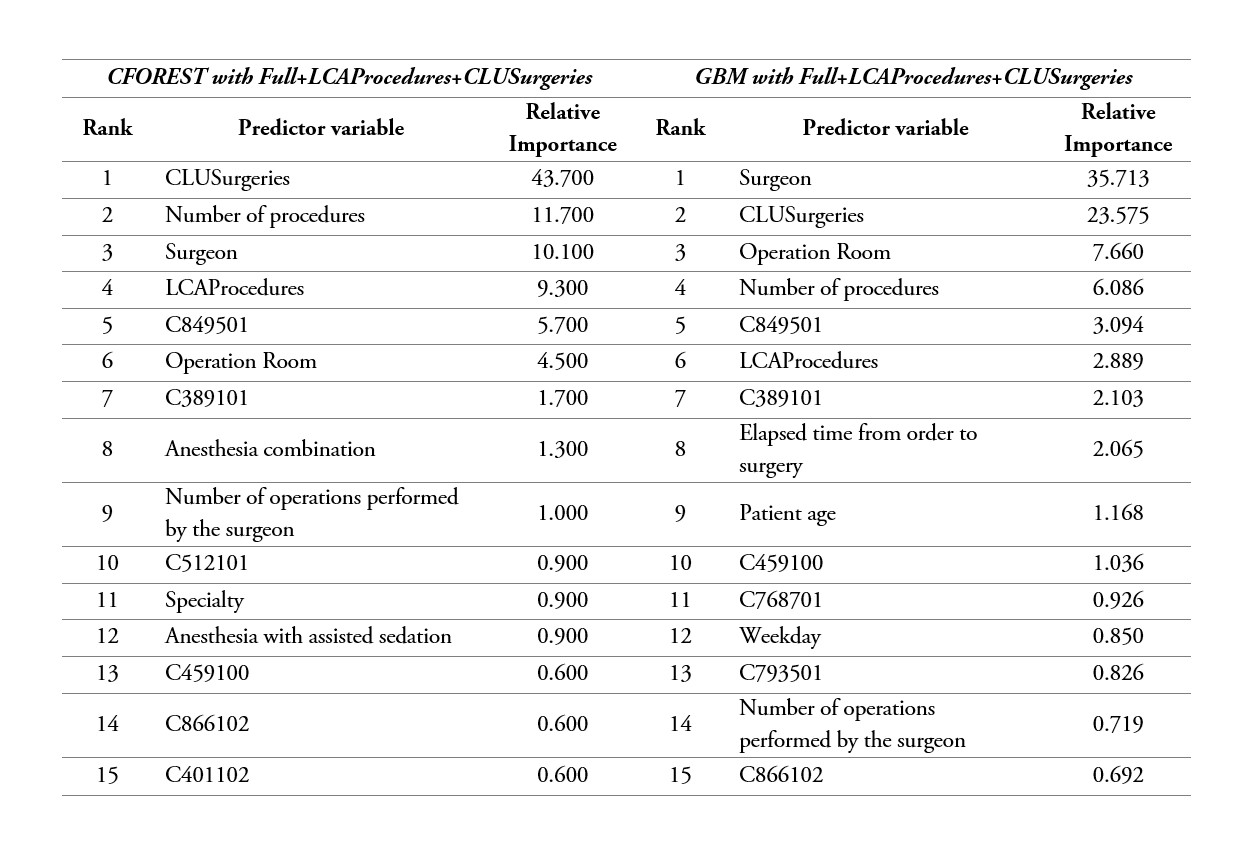
Source: Own elaboration
Conclusions
In this study, we investigated different configurations of models and variables to obtain an appropriate model to predict ORTs. The best model was obtained with GBM using the full data set that includes the multiple procedures as binary variables, plus the addition of the new variables obtained through the LCA and hierarchical clustering methods. This indicates that the proposed strategy, using the procedures as binary variables and including the cluster variables, could improve the performance of the prediction models in this type of problems, although it would be necessary to evaluate the methodology in multiple instances of data to have a clearer view of its effectiveness. The accuracy results with this model in the test set were: RMSE of 67.81 minutes, MAE of 44.85 minutes and an operational accuracy of 57.3%. Which means that the model provides ORT with an average deviation of 44.85 minutes from the real time of the OR. This value is influenced by the longer surgeries that generate greater difficulty in predicting, an effect that is magnified by the RMSE by squaring the deviations of the errors. As shown in figure 4, 52.7% of the cases have a maximum estimation error of ±30 minutes, and only 21.4% of the cases would have deviations or delays above 1 hour. Although this model is the one that generates the least bias (figure 3), we observe the difficulty all models have to predict high and atypical ORTs, which is an issue in different works in this field [13], [26]. Therefore, in that case, we will probably underestimate ORTs and cause delays in the next scheduled procedure. Fortunately, this situation is not frequent because only around 5.68% of the ORTs exceed 316 minutes (5.25 hours).
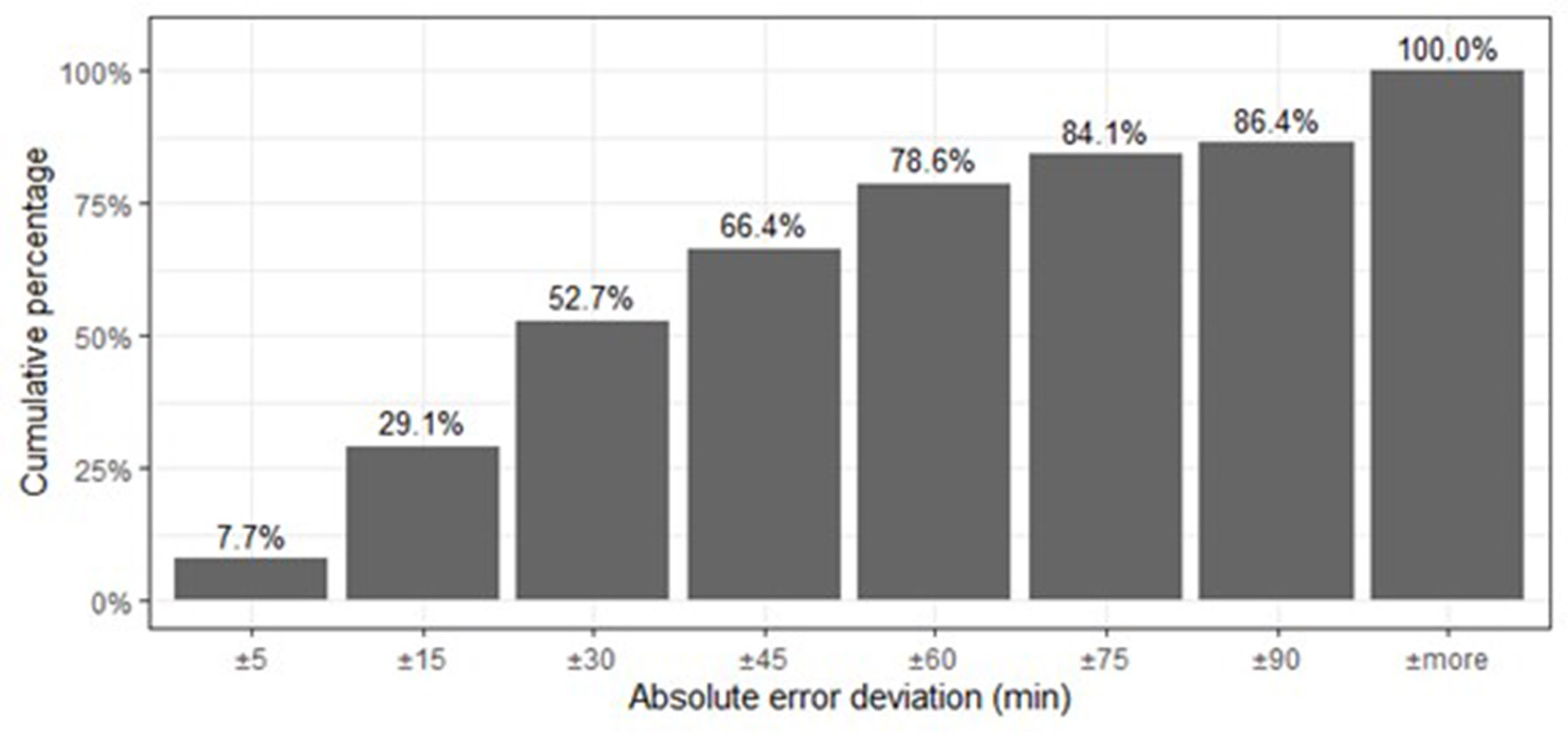 Figure 4
Accumulated percentage of cases on the test set whose estimation error is within the minute interval indicated on the x-axis. Estimated percentage for the model GBM with
Figure 4
Accumulated percentage of cases on the test set whose estimation error is within the minute interval indicated on the x-axis. Estimated percentage for the model GBM with
Full+LCAProcedures+CLUSurgeries
Source: Own elaboration
The Gradient Boosting Model (GBM) generates the best accuracy results in both scenarios with the Basic and Full data sets. Nonetheless, with the Basic variant, no significant difference was observed compared to the Conditional Random Forest (CFOREST) when the artificial variables were added. We evaluated a new modeling strategy based on the identification of latent subgroups of procedures that can be programmed in a surgery. For that purpose, we used Latent Class Analysis identifying six different groups of procedures. This LCA variable was evaluated in several prediction models, obtaining good results under all the scenarios. We can therefore conclude that including such variable improves prediction accuracy. As can be seen from table 5, the variable is among the most important factors in this study. Similarly, the variable created based on the clustering strategy with the use of basic predictors, showed an improvement in accuracy. This step was taken to obtain a compact and connected group of subjects that share surgical characteristics. Here, we found that the hierarchical method generates better cluster properties than its k-medoid counterpart, which was more unstable. For the Gower coefficient, we used the same weight for all the variables, meaning that all of them have the same importance in the clustering process. Nevertheless, a new strategy can be tested to assign different weights to each variable according to their impact on the variance reduction of the response variable.
Evaluating the importance of the variables in the final model, we found that the surgeon, the number of procedures, the operating room, LCAProcedures, CLUSurgeries and some specific procedures, are the most important variables in the prediction task. The specific room where the surgery was programmed is included because each room presents different conditions; some require more preparation and equipment conditioning, which implies more room time. This final model can be used for surgeries with multiple procedures; its purpose is to be integrated into an intelligence programming system where the prediction model will be automatically fed by the hospital's information systems and executed in the background with the scheduling optimization program. The latter will continually invoke the model, because one of the objectives of scheduling optimization is to define optimal ORTs in terms of efficiency and subject to surgery restrictions. Moreover, one of the most important variables in the prediction model is the OR. This interaction between the prediction model and the optimization algorithm could also be carried out by running the prediction model with every OR, storing the prediction time, and retrieving it when the scheduling optimization requires it. On the other hand, considering that the modeling process was restricted to the most frequent specialties and the objective is to have a predictive tool for all cases. As future work, we will explore the implementation of Bayesian models that include the knowledge of specialists in ORT prediction for cases with little or no history. Some works in this sense have been developed [47], although there is still room for improvement in this regard.
References
[1] World Health Organization, “World Health Statistics,” pp. 1-79, 2016, [Online]. Available: http://www.who.int/gho/publications/world_health_statistics/EN_WHS08_Full.pdf.
[2] P. A. Velásquez-Restrepo, A. K. Rodríguez-Quintero, & J. S. Jaén-Posada, “Aproximación metodológica a la planificación y a la programación de las salas de cirugía: una revisión de la literatura,” Revista Gerencia y Políticas de Salud, vol. 12, no. 24, pp. 249-266, 2013. https://doi.org/10.11144/Javeriana.rgsp12-24.ampp
[3] WHO Regional Office for Europe, “European Health Information Gateway, Inpatient surgical procedures per year per 100 000,” 2018. Accessed on: Nov. 02, 2018. Available: https://gateway.euro.who.int/en/hfa-explorer/).
[4] DANE, “En el día mundial de la población el DANE le cuenta,” 2018. Accessed on: Nov. 09, 2018. [Online]. Available: https://www.dane.gov.co/files/comunicados/Dia_mundial_poblacion.pdf.
[5] K. Guzmán Finol & Banco de la República de Colombia, “Radiografía de la oferta de servicios de salud en Colombia,” 202, 2014. [Online]. Available: http://www.banrep.gov.co/docum/Lectura_finanzas/pdf/dtser_202.pdf.
[6] N. Bahou, C. Fenwick, G. Anderson, R. van der Meer, & T. Vassalos, “Modeling the critical care pathway for cardiothoracic surgery,” Health Care Management Science, vol. 21, no. 2, pp. 192-203, 2018. https://doi.org/10.1007/s10729-017-9401-y.
[7] S. A. Erdogan & B. T. Denton, “Surgery Planning & Scheduling: A Literature Review,” In Wiley Encyclopedia of operations research and management science, J. J. Cochran, Ed. New York: John Wiley & Sons, 2010. Available: https://www.researchgate.net/profile/Brian-Denton-2/publication/241142977_Surgery_Planning_and_Scheduling_A_Literature_Review/links/55ede81d08aef559dc438308/Surgery-Planning-and-Scheduling-A-Literature-Review.pdf
[8] Z. Shahabikargar, S. Khanna, A. Sattar, & J. Lind, “Improved prediction of procedure duration for elective surgery,” Studies in Health Technology and Informatics, vol. 239, pp. 133-138, 2017. https://doi.org/10.3233/978-1-61499-783-2-133
[9] G. Sagnol et al., “Robust allocation of operating rooms: A cutting plane approach to handle lognormal case durations,” European Journal of Operational Research, vol. 271, no. 2, pp. 420-435, 2018. https://doi.org/10.1016/j.ejor.2018.05.022.
[10] D. Duma & R. Aringhieri, “An online optimization approach for the Real Time Management of operating rooms,” Operations Research for Health Care, vol. 7, pp. 40-51, 2015. https://doi.org/10.1016/j.orhc.2015.08.006.
[11] T. Knoeff, E. W. Hans, & J. L. Hurink, “Operating room scheduling an evaluation of alternative scheduling approaches to improve OR efficiency and minimize peak demands for ward beds at SKB Winterswijk,” M.S. thesis, Dept. Operational Methods for Production and Logistics, Twente Univ., Enschede, Netherlands, 2010. Available: https://essay.utwente.nl/60822/1/MSc_Thijs_Knoeff.pdf.
[12] J.-S. Tancrez, B. Roland, J.-P. Cordier, & F. Riane, “Assessing the impact of stochasticity for operating theater sizing,” Decision Support Systems, vol. 55, no. 2, pp. 616-628, May 2013. https://doi.org/10.1016/J.DSS.2012.10.021
[13] J. M. van Oostrum, T. Parlevliet, A. P. M. Wagelmans, & G. Kazemier, “A method for clustering surgical cases to allow master surgical scheduling,” INFOR, vol. 49, no. 4, p. 37, 2008. https://doi.org/10.3138/infor.49.4.254.
[14] J. Jang, H. H. Lim, G. Bae, S. U. Choi, & C. H. Lim, “Operation room management in Korea: Results of a survey,” Korean Journal of Anesthesiology, vol. 69, no. 5, pp. 487-491, 2016. https://doi.org/10.4097/kjae.2016.69.5.487.
[15] D. P. Strum, A. R. Sampson, J. H. May, & L. G. Vargas, “Surgeon and Type of Anesthesia Predict Variability in Surgical Procedure Times,” Anesthesiology, vol. 92, no. 5, pp. 145-1466, 2000.
[16] M. J. C. Eijkemans, M. van Houdenhoven, N. Tien, E. Boersma, E. W. Steyerberg, & G. Kazemier, “Predicting the Unpredictable. A New Prediction Model for Operating Room Times Using Individual Characteristics andt he Surgeon’s Estimate,” American Society of Anesthesiologists, vol. 112, no. 1, pp. 41-49, 2010. https://doi.org/10.1016/j.jacc.2015.12.063.
[17] V. Bellini, M. Guzzon, B. Bigliardi, M. Mordonini, S. Filippelli, & E. Bignami, “Artificial Intelligence: A New Tool in Operating Room Management. Role of Machine Learning Models in Operating Room Optimization,” Journal of Medical Systems, vol. 44, no. 1, pp. 1-10, 2020. https://doi.org/10.1007/s10916-019-1512-1
[18] E. Kayis et al., “Improving prediction of surgery duration using operational & temporal factors,” AMIA Annual Symposium Proceedings, vol. 2012, pp. 456-62, 2012. https://pubmed.ncbi.nlm.nih.gov/23304316/
[19] P. S. Stepaniak, C. Heij, & G. de Vries, “Modeling and prediction of surgical procedure times,” Statistica Neerlandica, vol. 64, no. 1, pp. 1-18, February 2010. https://doi.org/10.1111/j.1467-9574.2009.00440.x
[20] A. Wu, D. E. Rinewalt, R. W. Lekowski, & R. D. Urman, “Use of Historical Surgical Times to Predict Duration of Primary Aortic Valve Replacement,” Journal of Cardiothoracic and Vascular Anesthesia, vol. 31, no. 3, pp. 810-815, 2017. https://doi.org/10.1053/j.jvca.2016.11.023
[21] E. C. Lorenzi, S. L. Brown, & K. Heller, “Predictive Hierarchical Clustering: Learning clusters of CPT codes for improving surgical outcomes,” Machine Learning for Healthcare, vol. 68, 2017 [Online]. Available: http://mucmd.org/CameraReadySubmissions/52%5CCameraReadySubmission%5CMLHC_2017_FINAL_cameraready.pdf.
[22] N. Spangenberg, M. Wilke, & B. Franczyk, “A Big Data architecture for intra-surgical remaining time predictions,” Procedia Computer Science, vol. 113, pp. 310-317, 2017. https://doi.org/10.1016/j.procs.2017.08.332
[23] J. P. Tuwatananurak et al., “Machine Learning Can Improve Estimation of Surgical Case Duration: A Pilot Study,” Journal of Medical Systems, vol. 43, no. 3, pp. 1-7, March 2019. https://doi.org/10.1007/s10916-019-1160-5.
[24] M. A. Bartek et al., “Improving Operating Room Efficiency: Machine Learning Approach to Predict Case-Time Duration,” Journal of the American College of Surgeons, vol. 229, no. 4, pp. 346-354, 2019. https://doi.org/10.1016/j.jamcollsurg.2019.05.029
[25] J. K. Vermunt & J. Magidson, “Latent class cluster analysis,” in Applied latent class analysis, Cambridge, MA: Cambridge University Press, Ed. 2002, pp. 89-106.
[26] J. K. Vermunt & J. Magidson, “Latent class analysis,” in The Sage Encyclopedia of Social Sciences Research Methods, M. Lewis-Beck, A. Bryman and T. F. Liao, Eds. Thousand Oakes: Sage, 2004, pp. 549-553.
[27] I. C. Wurpts & C. Geiser, “Is adding more indicators to a latent class analysis beneficial or detrimental? Results of a Monte-Carlo study,” Frontiers in Psychology, vol. 5, p. 920, 2014. https://doi.org/10.3389/fpsyg.2014.00920
[28] D. A. Linzer & J. B. Lewis, “poLCA: An R Package for Polytomous Variable Latent Class Analysis,” Journal of Statistical Software, vol. 42, no. 10, pp. 1-29, 2011. https://doi.org/10.1037/a0037069
[29] M. von Davier, “Bootstrapping Goodness-of-Fit Statistics for Sparse Categorical Data,” Methods of Psychological Research Online, vol. 2, no. 2, pp. 29-48, 1997. https://psycnet.apa.org/record/2002-14070-002
[30] S. Trivedi, Z. A. Pardos, & N. T. Heffernan, “The Utility of Clustering in Prediction Tasks,” arXiv, no. September, pp. 1-11, 2015.
[31] M. Maechler, P. Rousseeuw, A. Struyf, M. Hubert, & K. Hornik, “Cluster Analysis Basics and Extensions,” pp. 29-31, 2017.
[32] T. Hastie, R. Tibshirani, & J. Friedman, The Elements of Statistical Second Edition Learning: Data Mining, Inference, and Prediction, Second Ed. Berlin: Springer Science+Business Media, 2009.
[33] J. Han, M. Kamber, & J. Pei, Data mining: concepts and tecniques, Third Ed. Amsterdam, Netherlands: Elsevier Inc., 2012.
[34] M. Maechler, P. Rousseeuw, A. Struyf, M. Hubert, & K. Hornik, “Cluster Analysis Basics and Extensions. R package version 2.0.7-1”, 2018 [Online]. Available: https://cran.r-project.org/web/packages/cluster/cluster.pdf
[35] J. Handl, J. Knowles, & D. B. Kell, “Computational cluster validation in post-genomic data analysis,” Reverse Complement, vol. 21, no. 15, pp. 3201-3212, 2005. https://doi.org/10.1093/bioinformatics/bti517
[36] P. J. Rousseeuw, “Silhouettes: A graphical aid to the interpretation and validation of cluster analysis,” Journal of Computational and Applied Mathematics, vol. 20, pp. 5-65, November 1987, https://doi.org/10.1016/0377-0427(87)90125-7
[37] T. Therneau, B. Atkinson, & B. Ripley, “rpart: Recursive Partitioning and Regression Trees. R package version 4.1-11.” 2017,[Online]. Available: https://cran.r-project.org/package=rpart.
[38] L. Breiman, “Random Forests,” 2001. Accessed: Dec. 02, 2018 [Online]. Available: https://link.springer.com/content/pdf/10.1023%2FA%3A1010933404324.pdf.
[39] T. Hothorn, P. Buehlmann, S. Dudoit, A. Molinaro, & M. Van Der Laan, “Survival Ensembles,” Biostatistics, vol. 7, no. 3, pp. 355-373, 2006.
[40] T. Hothorn, K. Hornik, & A. Zeileis, “Unbiased recursive partitioning: A conditional inference framework,” Journal of Computational and Graphical Statistics, vol 15, no. 3, pp. 651-674, 2006. https://doi.org/10.1198/106186006X133933
[41] C. Strobl, A. L. Boulesteix, A. Zeileis, & T. Hothorn, “Bias in random forest variable importance measures: Illustrations, sources and a solution,” BMC Bioinformatics, vol. 8, no. 25, 2007. https://doi.org/10.1186/1471-2105-8-25.
[42] J. H. Friedman, “Greedy Function Approximation : A Gradient Boosting Machine,” Institute of Mathematical Statistics, vol. 29, no. 5, pp. 1189-1232, 2001, https://doi.org/10.1214/009053606000000795
[43] B. Greenwell, B. Boehmke, J. Cunningham, & G. Developers, “GBM: Generalized Boosted Regression Models. R package version 2.1.4.” 2018 [Online]. Available: https://cran.r-project.org/package=gbm.
[44] N. Master, Z. Zhou, D. Miller, D. Scheinker, N. Bambos, & P. Glynn, “Improving predictions of pediatric surgical durations with supervised learning,” Journal Name, International Journal of Data Science and Analytics, vol. 4, no. 1, pp. 35-52, August 2017, https://doi.org/10.1007/s41060-017-0055-0.
[45] M. Fairley, D. Scheinker, & M. L. Brandeau, “Improving the efficiency of the operating room environment with an optimization and machine learning model,” Health Care Management Science, vol. 22, no. 4, pp. 756-767, December 2019, https://doi.org/10.1007/s10729-018-9457-3.
[46] M. Kuhn et al., “caret: Classification and Regression Training. R package version 6.0-80.” 2018 [Online]. Available: https://cran.r-project.org/package=caret
[47] F. Dexter & J. Ledolter, “Bayesian Prediction Bounds and Comparisons of Operating Room Times Even for Procedures with Few or No Historic Data,” Anesthesiology, vol. 103, no. 6, pp. 1259–1167, 2005,https://doi.org/10.1097/00000542-200512000-00023.
Notes
*
Research paper
Author notes
a Corresponding author. E-mail: eduardganan@itm.edu.co
Additional information
How to cite this article: E. Gañan-Cardenas, J. I. Pemberthy-R, J. C. Rivera, and M. C. Mendoza-Arango, “Operating Room Time Prediction: An Application of Latent Class Analysis and Machine Learning”, Ing. Univ., vol. 26, 2022 [Online]. https://doi.org/10.11144/Javeriana.iued26.ortp







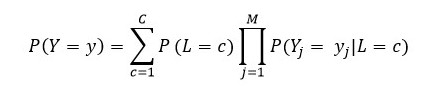 (1)
(1)
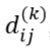 , a value between [0.1] measuring the dissimilarity between subjects (𝑖,𝑗) on variable 𝑘; and 𝑝, the number of variables in the data set [
, a value between [0.1] measuring the dissimilarity between subjects (𝑖,𝑗) on variable 𝑘; and 𝑝, the number of variables in the data set [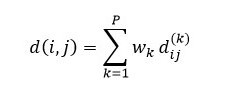 (2)
(2)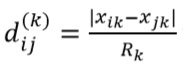 where 𝑅𝑘 = max(𝑥𝑘) − min (𝑥𝐾), is the full range of variable 𝑘.
where 𝑅𝑘 = max(𝑥𝑘) − min (𝑥𝐾), is the full range of variable 𝑘. 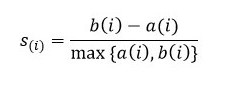 (3)
(3)
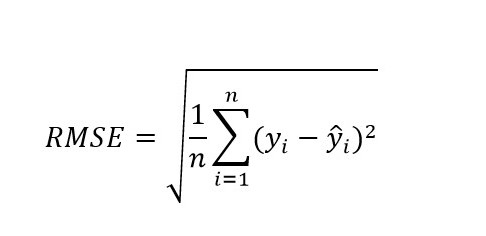 (4)
(4)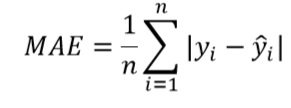 (5)
(5)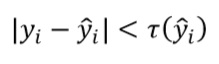 (6)
(6)