Introduction
Currently, the measurement of contaminants in hydrological resources, especially rivers, is done through the usage of highly specialized, bulky and very expensive equipment that allows the corresponding governmental protection agencies to verify the quality of the water, and determine whether it is polluted. In Colombia, the Institute of Hydrology, Meteorology and Environmental Studies (IDEAM) is in charge of this monitoring and the corresponding actions to preserve our hydrological resources, which are being depleted year after year.
The IDEAM has proposed and utilizes the Water Contamination Index (WCI) to map the status of the different rivers in the country. Different variables are acquired and weighted to calculate this index: dissolved oxygen, total suspended solids, chemical oxygen demand, electrical conductivity (also known as water conductivity) and pH. However, these monitoring campaigns demand an impressive logistical effort to bring all the required equipment and personnel to remote areas, making them very expensive. Therefore, the IDEAM is only capable of executing these campaigns two to three times a year [1]. With that in mind, it is necessary the design of a low-cost sensor that enables a massive monitoring of the rivers.
To that end, we considered the usage of an inter-digital capacitance (IDC), which has been previously tested to detect water contaminants [2], [3], [4]. An IDC sensor generates an electric field between its electrodes that interacts with the material under test (MUT) and, depending on the composition of the MUT (more specifically, its permittivity), the capacitance of the sensor varies [5]. The behavior of the sensor is similar to what happens when the dielectric material of a capacitor is modified. Some related work has shown that it is possible to identify the existence of dissolved solids in the water by using this type of sensor [6], [7]; however, these methods use complex laboratory equipment in order to acquire the value of the sensor, which cannot be included in a portable and scalable solution. Considering this, a computationally cheap mechanism to measure this type of sensor should be designed and implemented. Such a mechanism should consider the restrictions of a low-cost embedded platform: low computational resources, small memory and low power consumption.
Considering this scenario, an acceptable trade-off would be the continuous monitoring of just a few variables, with very low- cost (and low-accuracy) sensors. Such a system would allow IDEAM to have a wide view of the situation, not necessarily very accurate but good enough to prioritize these costly campaigns only to regions where suspicious behaviors seem to be occurring. With this in mind, we proposed and implemented a IoT-based solution to monitor rivers by using a portable device that integrates the IDC sensor that allows us to differentiate between clean and polluted water. Although we have implemented the complete IoT-based system, this paper focuses on the design and implementation of the IDC sensor, as well as the methods to measure its capacitance on a low-cost embedded platform.
The rest of the paper is organized into the following sections: Section II presents related work about IDC sensors and embedded measuring mechanisms; Section III describes the architecture and corresponding modules of the proposed solution; Section IV explains in detail the design and implementation of the IDC sensor; Section V presents the implementation of two embedded methods to measure capacitors; Section VI evaluates the performance of the solution; and Section VII presents our conclusions and future work.
Related work
RF and microwave techniques have been applied for dielectric properties measurement of materials. Properties such as conductivity, permeability and permittivity of lossy materials can be measured with different techniques. A comprehensive historical review of techniques and good practice guidelines are presented in [8]. For liquids, authors in [9] reviewed and classified the different techniques into reflectometry, transmission, resonance, time-domain and capacitance-cell methods. The IDC technique is a capacitance-cell method for liquid dielectric characterization at low frequencies, typically below 10 MHz, in which is very important to establish the static permittivity of liquids used to compute their complex permittivity at any given frequency in the RF and microwave range. An overview of the IDC technique is presented in [10].
More recently, non-invasive and non-destructive measurements have been proposed with IDC sensors for different applications, where dielectric characterizations have been carried out in order to measure other material properties, such as, power cable insulation damage detection [11], meat moisture content [12] and blood glucose monitoring [13]. Looking into the literature for similar approaches, the authors in [14] and [15] have already reported the use of IDC sensors for water pollutant measurements; nevertheless, the measurement method uses a specialized laboratory equipment to perform impedance spectroscopy, therefore it does not allow measurements to be made in the observation site.
In terms of the measuring mechanism, there are related techniques that have been implemented in microcontrollers to measure capacitors. Some include external circuitry, e.g., an external voltage comparator, to measure the charging time of a capacitor [16], but in despite of its simplicity, the utilization of external components increases the power consumption of the final solution. The work in [17] proposes the measurement of several charging cycles in the capacitor to obtain a capacitance value that is independent of the voltage applied, and only a function of the measured times, and the resistor value attached to the charging circuit. Although the measure of the capacitance obtained 1pF of confidence, the authors report a dynamic range of 33 pF up to 4.7 nF. The authors in [18] developed a mechanism that also requires external calibration components (impedance estimation) in order to achieve an acceptable accuracy. Similar work has proposed more accurate mechanisms that require the integration of external expensive operational amplifiers [19]. In other cases, the capacitance value is acquired by the usage of nonlinear equations, which increases the internal complexity of the system [20].
Our work proposes the design and implementation of a low-cost IDC sensor that enables in-site characterization of water samples by integrating such a sensor into a portable system. At the same time, we propose the design, implementation and comparison of two embedded acquisition techniques with the goal of having a low number of external devices (to reduce the cost and power consumption of the system), no calibration process, low computational complexity and acceptable accuracy. Our first approach considers a time-based mechanism that utilizes the microcontroller’s fast internal ADC, while our second frequency-based mechanism increases the accuracy of the measurements by implementing an embedded FFT.
Proposed solution
Figure 1 presents the general architecture of the proposed solution, which is composed of three main stages. The first stage comprises the design and characterization of the sensor, aiming for the capacitance to become large enough to allow an appropriate reading using a microcontroller. The second stage consists in the design of the routines for the microcontroller that will capture and read the values given by the sensor. Two methods were implemented and compared to determine which one was more appropriate for the IDC sensor and the limitations of an embedded platform. The last stage is oriented to develop an interaction interface between the user and the microcontroller system. This interaction can be achieved using both, a mobile device and an online server-based interface.
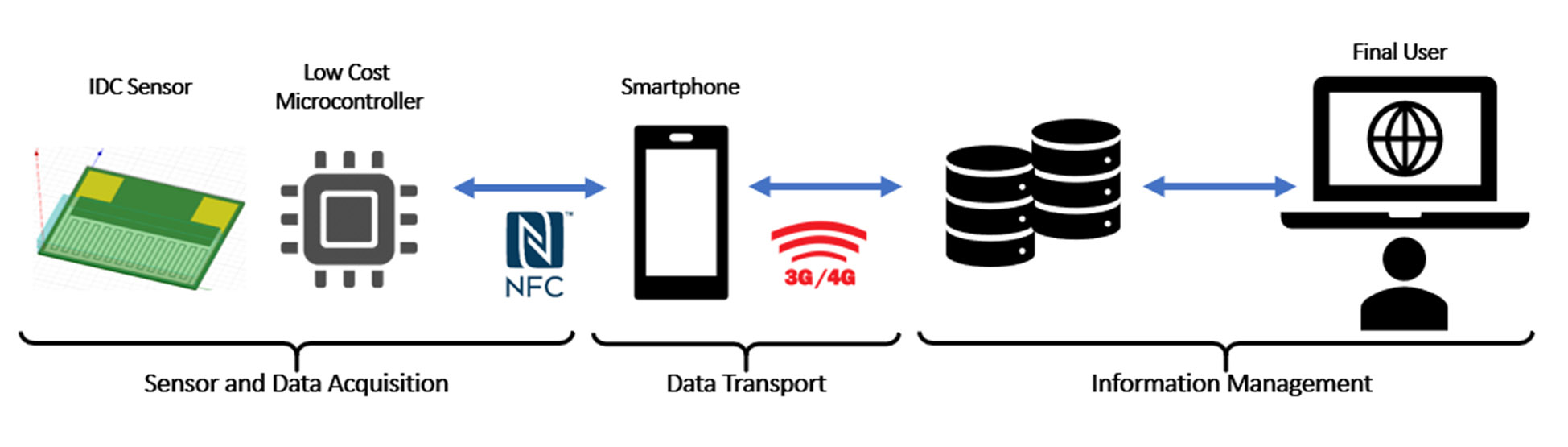 Figure 1
General architecture of the complete system
Figure 1
General architecture of the complete system
Source: Own elaboration
Sensor and Data Acquisition
The process of acquiring the data from the sensor comprises two main tasks: First, the water quality sensor design, its measurement range and the topology of the IDC. Second, the development of an effective mechanism to determine the value of the sensor through a low-cost microcontroller.
-
Water Quality Sensor: An IDC was selected to determine the presence of contaminant material in the water due to its simple fabrication process and low cost. Additionally, some reports have discussed its use in water quality measurement applications [2]. One of the most important criteria when designing an IDC for this application, is related to its capacitance value that must be large enough to facilitate the implementation of the measurement method, since the IDC will be integrated to an embedded system.
The IDC was designed using the conformal mapping technique, as discussed in [3]. Subsequently, the designed IDC was simulated using ANSYS to estimate the possible variation values when used to measure the water conductivity. An in-depth presentation of the sensor will be made in Section IV.
-
Measurement Method: The selected measurement method must incur in low power consumption since it must be implemented in a resource-limited microcontroller. In fact, the selection of the microcontroller is based on the selected measurement method. Since one of the considered methods involved determining the capacitance value using a frequency analysis and an oscillator circuit, it is desirable to select a microcontroller that includes a floating-point unit (FPU) to accelerate the calculations of a possible embedded Fast Fourier Transform (FFT). Another restrictive parameter is the operating frequency of the analog-to-digital converter (ADC) due to the nature of the physic variable that is aimed to acquire, i.e., capacitance. Finally, an STM32F407VGT6 microcontroller (ARM Cortex-M4 processor with an FPU) was selected, which is widely used as it is incorporated in the STM32f4-Discovery development board. Section V presents the details of the design and implementation of the measurement method.
Data storage is supported by an EEPROM memory (STM M24LR16E 16-Kbit, organized in 512 blocks of 32-bits). Every measurement acquired from the IDC sensor is stored in two blocks: one block holds the four most significant bytes of the value, and the second one holds the least significant bytes, corresponding to the decimal part. The microcontroller stores the capacitance value read from the sensor, while a mobile application is in charge of determining the correspondent water conductivity, that in turn, is subsequently stored in an on-line server. An NFC antenna is used to provide connectivity between the embedded system and the mobile application.
Data Transport Layer
In order to easily scale the solution and reduce the costs of providing a dedicated communication module, the data transport layer is based on the communication capabilities of a typical smart-phone and an Android application. The mobile application is in charge of: i) reading the EEPROM memory through an NFC connection (available in most of today’s smart-phones); ii) transforming the read capacitance value to a water quality level; iii) visualizing the acquired values; and, iv) centralizing the information to an online server 1.
Information Management
Two variables are sent to the Ubidots server, i.e., the capacitance reading taken by the microcontroller and the water conductivity calculated from the obtained capacitance. Both variables are stored considering the time of arrival, which in turn, allows the visualization of a data log. The server can be accessed by the final user who can revise, visualize and download the data of interest. Furthermore, the administrator can reset the entire data base and program the generation of alert messages when a specific threshold is surpassed.
Based on both obtained values (the capacitance and the water conductivity), the system will classify every datum in one of 4 possible states, which represent the concentration of salt dissolved in the water. The first range corresponds to water that is completely clean, while the subsequent ranges represent low, medium and high salt concentrations, respectively, which are also coded into an integer number between 1 to 4 to ease the visualization process. The result of the classification is sent to the Ubidots server as a third variable, that at the end, is the characteristic that the final user will use to have an idea of the level of pollution of the water samples.
Inter-digital capacitance (IDC) sensor design
Part of our preliminary work was focused on identifying clear relationships between the capacitance of the sensor and a parameter of the water sample. After testing how the permittivity of the water changed with variations of dissolved oxygen, pH and conductivity; we found that the latter has the best behavior. As shown in figure 2, as the conductivity of the water increases, the capacitance also increases, almost following a linear form. In this test, incremental amounts of salt (steps of 10gr) were added to a 2-liter recipient with water, modeling different samples of contaminated water with dissolved solids. With this result, it seems possible to characterize a sample of contaminated water by measuring its permittivity with an IDC sensor.
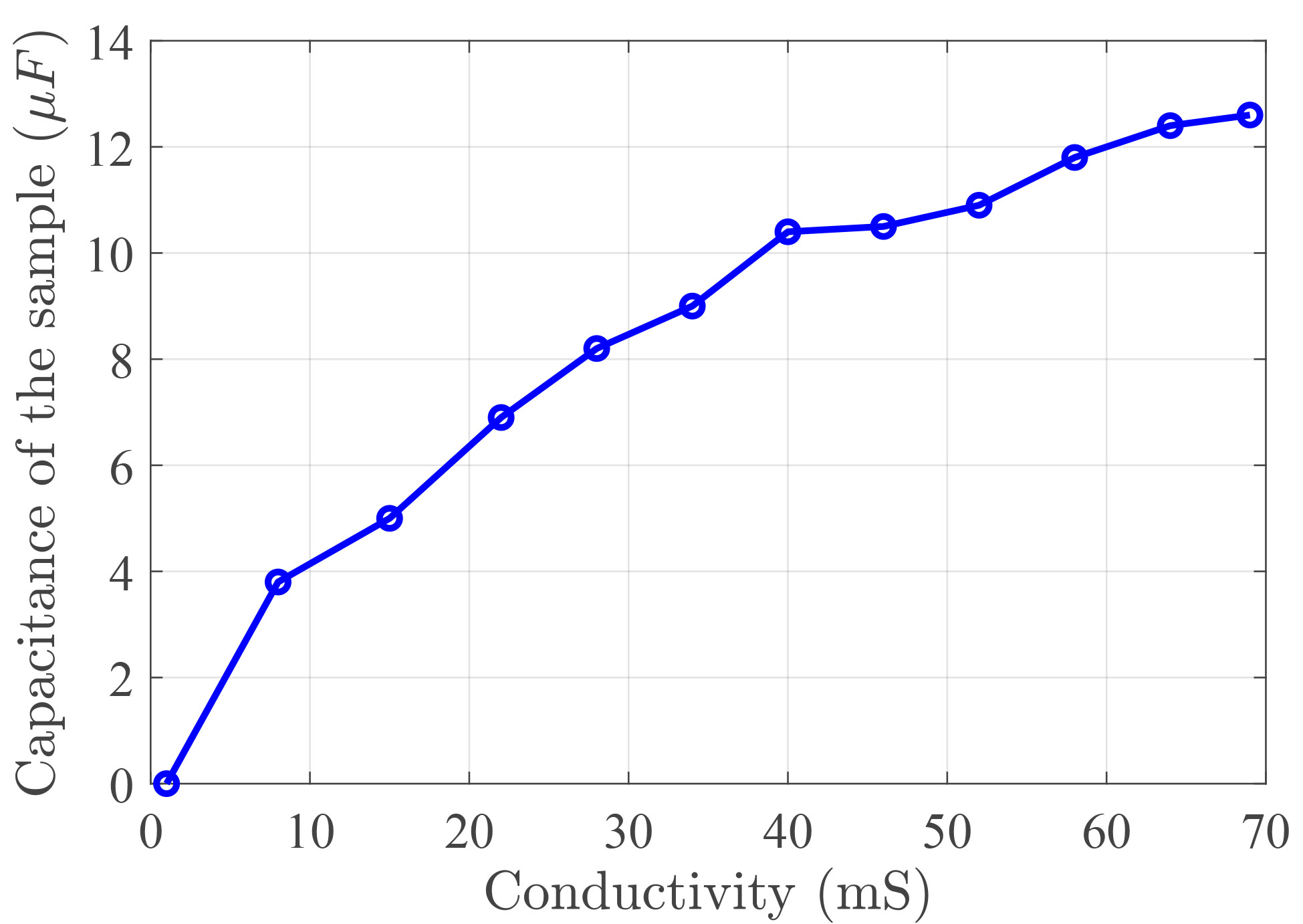 Figure 2
Relationship between the conductivity and the capacitance of contaminated water
Figure 2
Relationship between the conductivity and the capacitance of contaminated water
Source: Own elaboration
IDC Head Sensor Design Model
In order to determine the dimensions of the sensor, an analysis of an IDC is carried out by using the conformal mapping technique [6]. According to this technique, the capacitance value can be analyzed by modeling a capacitor in a set of layers, in which, each layer represents an element that interacts with the electric field generated by the conductor. It is defined that the value of an IDC has a base capacitance determined by the size of the fingers, one due to the material on which the conductor is located and another due to the insulating layer located on the sensor. In [6] it is assumed a non-homogeneous conformal coplanar transmission line structure where the total line capacity between the signal strip and the adjacent ground plane is the sum of the line capacity C1 and C2, having C1 as the line capacity of an homogeneous coplanar transmission line with air and C. as the capacitance of a non-homogeneous coplanar transmission line with a dielectric substrate layer with a relative constant εs − 1 given that air region is already included in the calculation of C1. figure 3(a) shows a cross-section view of the sensor model where a, b are the finger’s width and d corresponds to the distance between them.
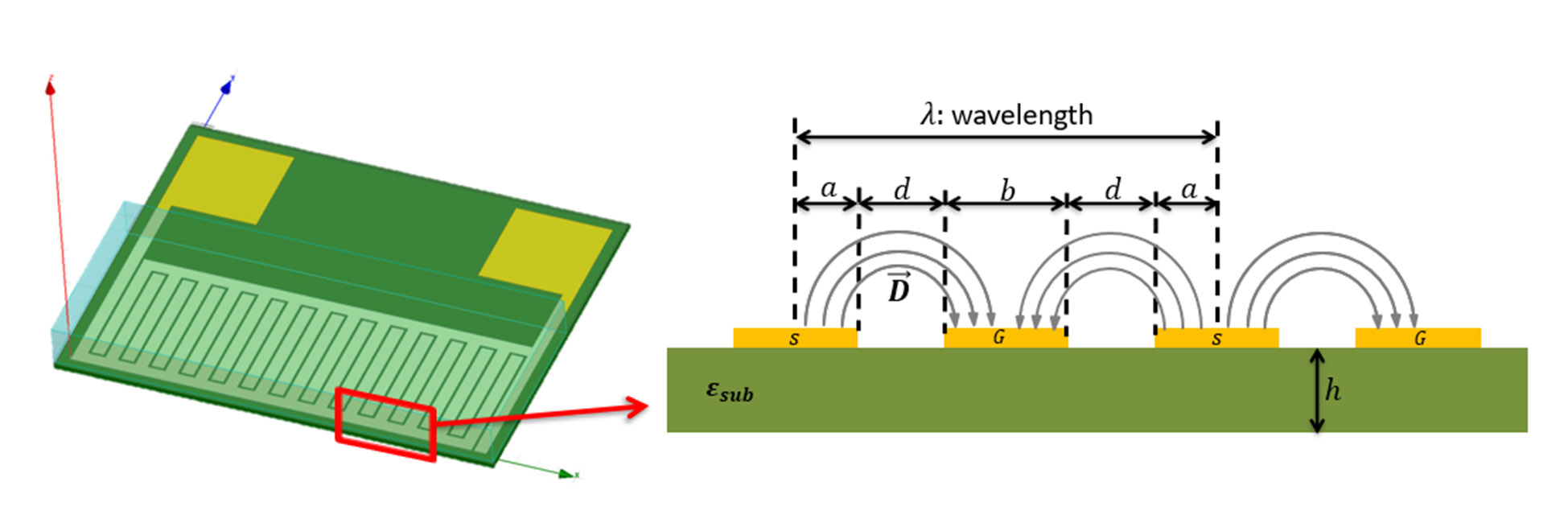 Figure 3
a) Simulation model and cross-section view of a coplanar strip line. b) Electric field intensity
Figure 3
a) Simulation model and cross-section view of a coplanar strip line. b) Electric field intensity

Source: Own elaboration
In the designed model, the computation of the base capacitance C1 in the absence of the dielectric substrate involves two conformal mapping transformations in order to obtain an equivalent two parallel plates model from where it is possible to compute the plate separation K(k1) and the plate width K(k1’). By applying equation 1 it is possible to compute the capacitance value C1.
where K(k1) is the complete elliptical integral of the first kind with module k1, K(k’1)= K’(k1) being the derivative of the elliptical integral function, ε
0
is the free space permittivity constant and K(k’1)/ K(k1) is the ratio of a complete elliptical integral of the first kind which can be evaluated by the Hilberg’s approximation, given the expressions of k1 and k’1
by the equations in 2 and 3, respectively.
Equations 1 and 2 show the direct relationship between the finger’s size and separation, air permittivity and the capacitance value. Similarly, capacitance C2 is calculated by applying a conformal mapping transformation as before expressed by the equation 4:
where
Therefore, the total coplanar transmission line capacity between the signal strip and the adjacent ground plane is given by equation 7:
where n is the number of IDC finger pairs and l is the overlapping finger length. To measure the dielectric properties of aqueous materials with high conductivity, it is necessary to insulate the electrodes in order to avoid any electrical or electro-chemical interference. Thus, the capacitance effect of the additional layer must be taken into account by C3 when evaluating the total capacitance value of the IDC sensor. C3 is evaluated again by means of the conformal mapping technique as before but considering the thickness of the insulator layer hins
and its relative electric permittivity as ε
ins – 1.
IDC Head Sensor Design and Simulation
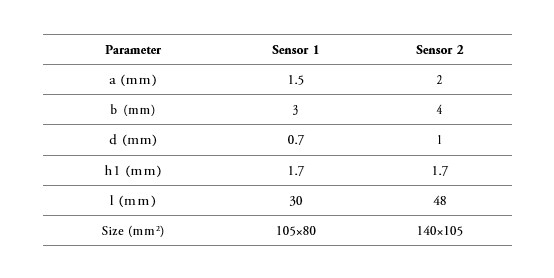
The initial requirements were strictly related with the sensor dimensions. For this reason, the initial fingers separation was set to less than 1 mm, the strip’s width to 3 mm and the finger’s length to 30 mm. A low-cost glass-reinforced epoxy laminate material (FR4) was selected as the substrate with a relative dielectric permittivity of εs = 4.4 and thickness h1
= 1.7 mm. Other parameters were defined according to similar works found in literature such as the number of IDC finger pairs that was initially set as 14.5. Additionally, a dielectric paint was set as the insulator layer with thickness h2 = 1 mm and a relative dielectric permittivity ofεins= 6. The overall set of initial parameters for the IDC head sensor were:α = 1.5 mm, b = 3 mm, d = 0.7 mm, h1 = 1.7 mm,
h2
= 1 mm, l = 30 mm, n = 14.5, εs = 4.4, εins= 6, obtaining an initial total capacitance of Ctotal = 58.15 pF.
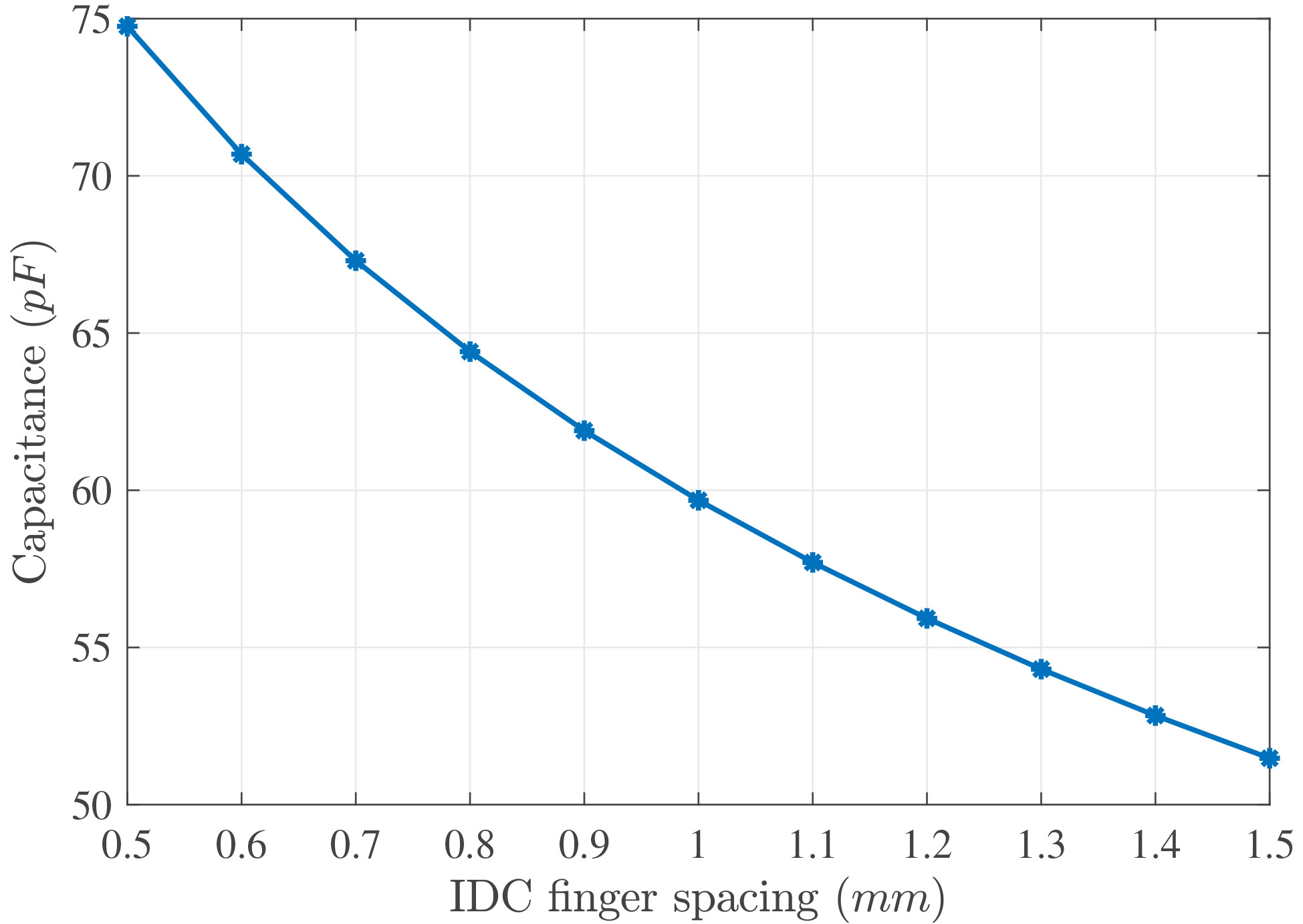
With the initial set of sensor parameters, an analysis of the dependence of the capacitance value regarding to the fingers width and separation was carried out. figure 4(a) shows the effect of different IDC finger widths on the total capacitance. It is possible to observe a strong dependence of the capacitance value as the fingers width varies from 2 mm to 8 mm, resulting in 16% of increase of the total capacitance value. In addition, the capacitance variation over different IDC finger spacing is shown in figure 4(b), for which the finger width is set to 3 mm and other parameters are set as before.
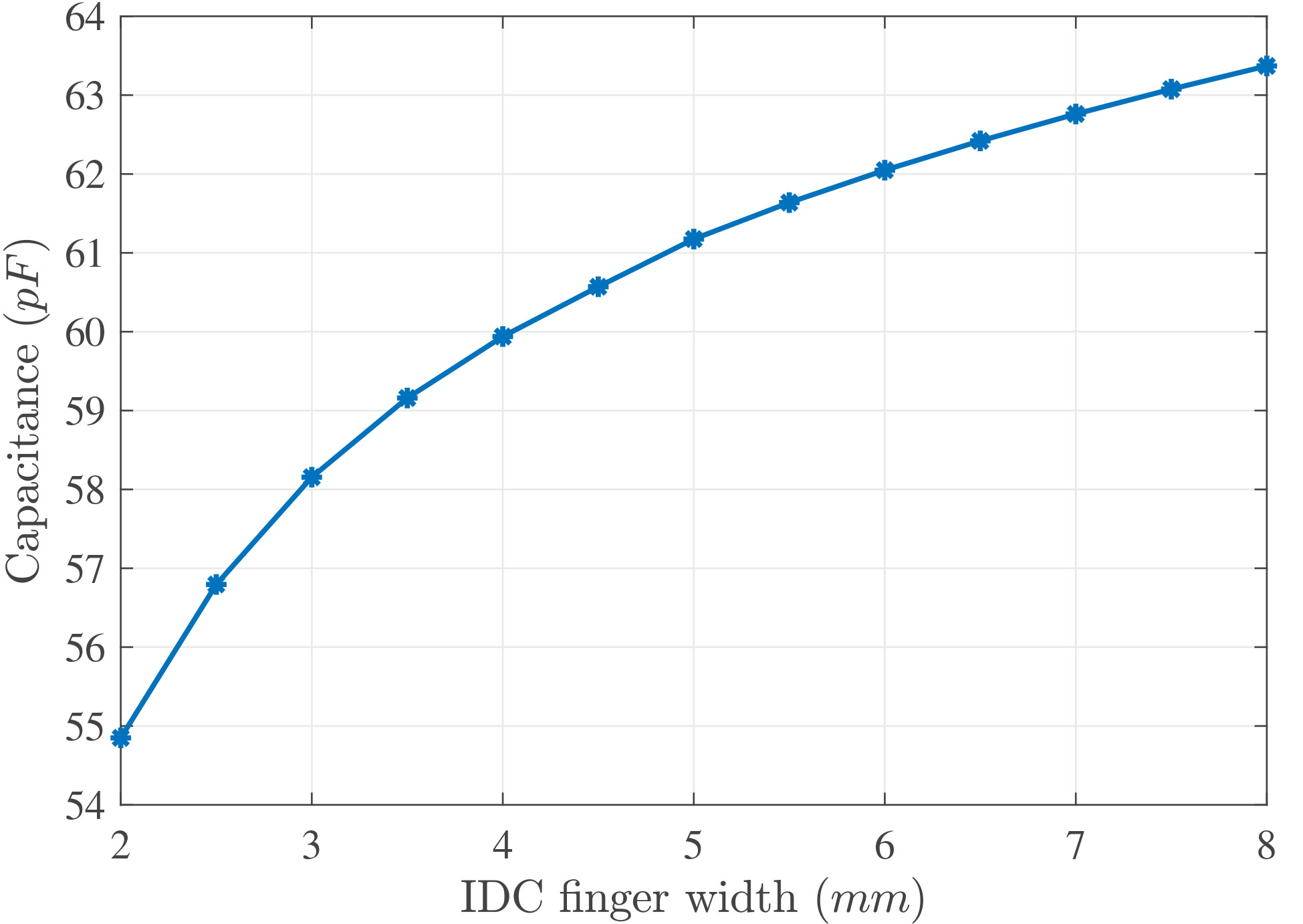 Figure 4
Capacitance over different IDC finger a) widths, b) spacings
Figure 4
Capacitance over different IDC finger a) widths, b) spacings
Source: Own elaboration
The relationship between the total IDC capacitance, the sensor wavelength λ and the insulation layer thickness h2 is a very important factor to design the final head sensing device. As shown in figure 5, the total IDC capacitance value reaches a saturation over h2/λ > 0.5 for different finger widths which, in other words, means that the IDC device is not sensitive when the MUT is half wavelength of distance over the head sensor. Therefore, with the initial dimensions aforementioned, the insulation layer thickness must be less than 3.7 mm in order for the sensor to characterize the MUT.
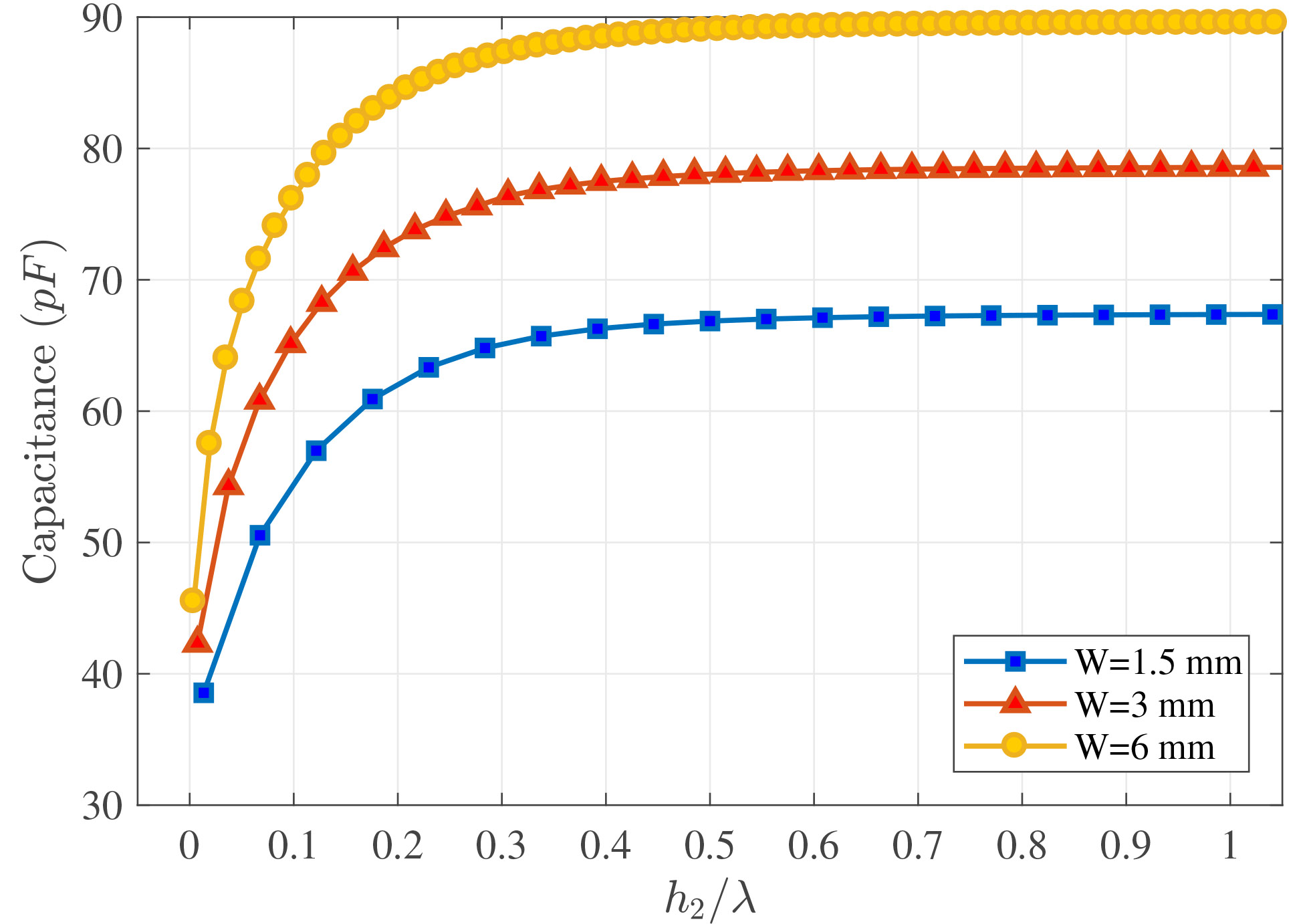 Figure 5
Total capacitance as a function of the normalized insulation layer thickness h2/λ, with λ = 2a + 2d + b
Figure 5
Total capacitance as a function of the normalized insulation layer thickness h2/λ, with λ = 2a + 2d + b
Source: Own elaboration
The simulation model of the final design employing ANSYS Maxwell is shown in figure 3(a) and the electric flux density field in air over the finger’s path is shown in 3(b). The total simulated capacitance is Ctotal = 62.81 pF, obtaining an error of 8%. figure 6 shows the calculated, simulated and measured total capacitance of the IDC with an impedance analyzer, from 20Hz until 100kHz, indicating a relative error between 20% and 30%, which is acceptable for this application.
In order to test variations for different capacitance values, two IDC head sensor models were implemented. The insulation layers (3 to 6 layers of paint) are very difficult to model in ANSYS and might be the reason for the error presented between the simulations and the characterization of the fabricated heads. table 1 shows the final parameters of the fabricated head sensors.
Proposed measurement methods
Considering the hardware limitations of this portable solution (low power consumption and computational capabilities), an appropriate measurement method must be selected and implemented. Two approaches to measure the capacitance of the sensor are proposed and evaluated. The first method consists in the measurement of the charging time of a capacitor in a simple resistor-capacitor (RC) circuit. The charging curve is tracked in time by a microcontroller and, consequently, it estimates the capacitance of the sensor based on how long it took to reach 50% of its maximum voltage. The second method attempts to measure the frequency of an external oscillator circuit which includes the IDC as part of its resonance impedance. It is possible to estimate the capacitance from the oscillating frequency, using a frequency domain approach that involves the estimation of a Fast Fourier Transform (FFT).
Charging Time Method
The voltage of a capacitor in an RC circuit is described by the solution of a first order differential equation. In particular, when the forcing signal is a constant voltage, the capacitor’s charging behavior corresponds to an exponential signal against time, and with a time constant τ = Resistance • Capacitance = R • C. To obtain the charging time, the microcontroller sets a GPIO as ‘1’ (5V), which is possible since the current load to the pin is very low, while at the same time the ADC starts to capture the voltage across the capacitor.
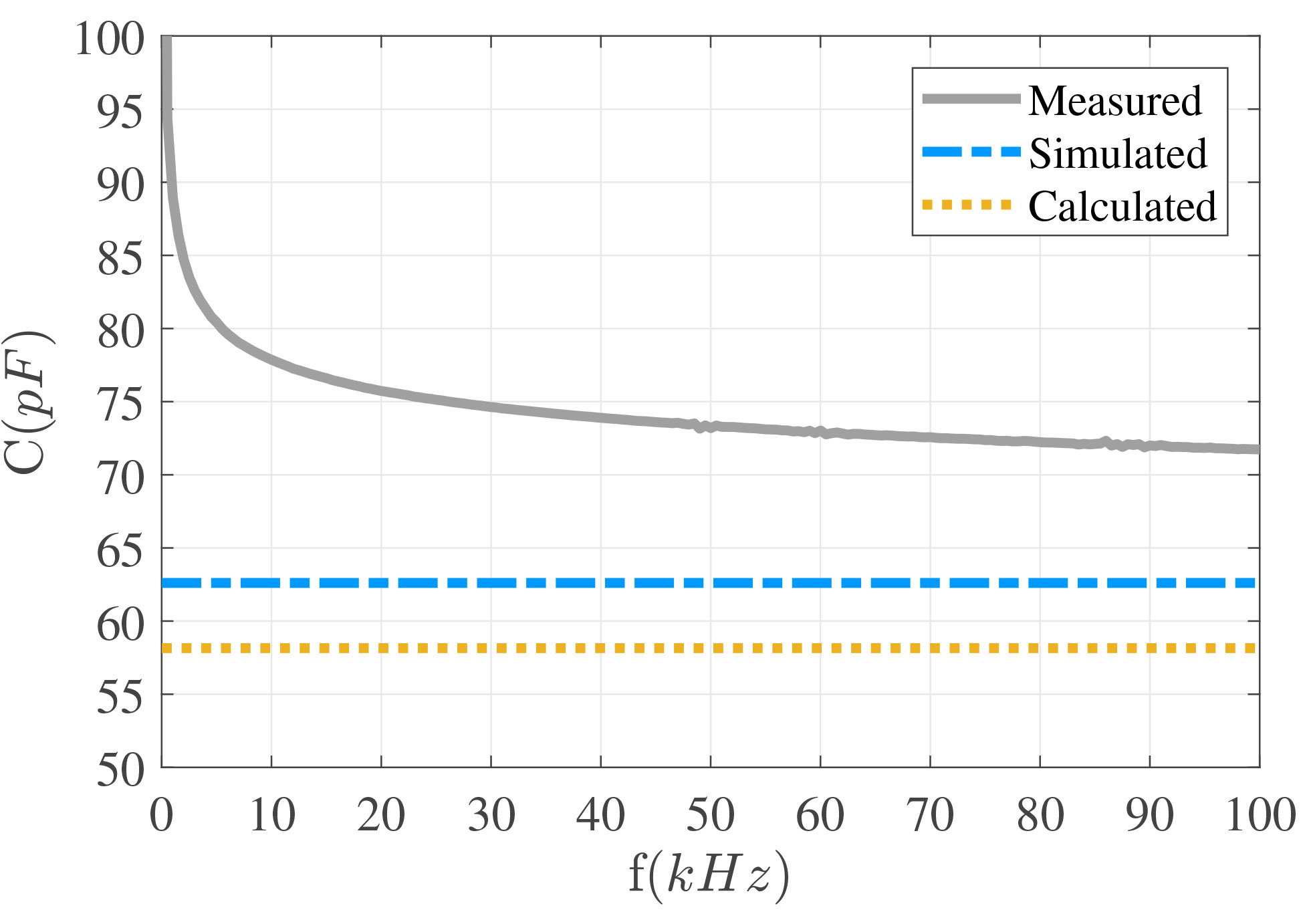 Figure 6
Figure 6
Measured, simulated and computed Capacitance
Source: Own elaboration
Table 1
Dimensions of the fabricated IDC head senso
Source: Own elaboration
The charging time method avoids the calibration by external means, while at the same time allows a fast calculation of the capacitance value. The possible capacitance range will depend on the ADC sampling rate and resolution (number of bits), while in general, this charging process is very fast and cheap, in terms of computational requirements.
The first design parameter is the ADC sampling rate, set at 564 kHz, meaning that the smallest capacitance value that the system can process should present a charging curve slow enough to allow the microcontroller to obtain enough samples to characterize it. The charging time of the capacitor will depend on the time constant of the circuit, which in turn is determined by the resistance times the capacitance. For this specific case, 50% of the maximum source voltage (Vin = 5V ) was selected as the reference voltage. Therefore, in equation 8 is possible to obtain the time that the capacitor takes to reach Vin/2 V, and subsequently the ratio between the capacitance and the charging time (for our experiments, R = 100kΩ).
Frequency Analysis Method
The second method used to estimate the capacitance value is based on a frequency analysis of an oscillator circuit. The oscillator circuit is built using a LM555 chip, in astable configuration, as shown in figure 7. For this particular application, the duty cycle is not important, thus the resistors R1
and R2 are set to have the same value (both selected to be 15KΩ), which in turn simplifies the design of the circuit.
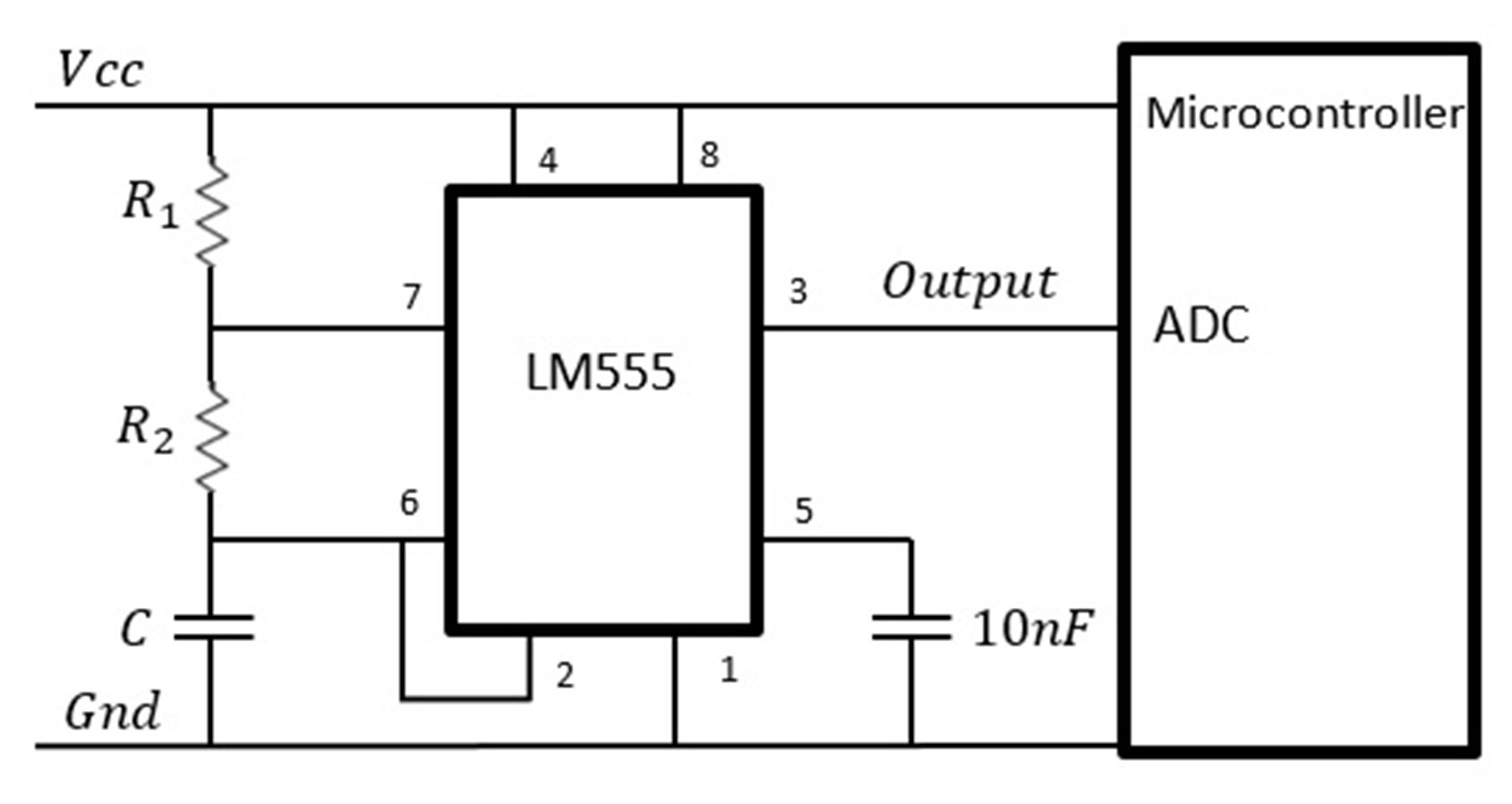 Figure 7
Astable oscillator circuit used. C is the IDC sensor
Figure 7
Astable oscillator circuit used. C is the IDC sensor
Source: Own elaboration
The oscillator circuit is connected to an ADC input of the microcontroller, which in turn reads the analog value of the oscillating signal. Subsequently, the microcontroller implements the FFT algorithm to find the frequency components of the input signal, and therefore, the fundamental oscillating frequency. The microcontroller reads and stores 1024 samples that are used to calculate the oscillating frequency and, therefore, capacitance value using equation 9.
In order to reach the Nyquist Theorem and taking into consideration the ADC’s sampling frequency (152kHz), the capacitance to be measured (IDC sensor) should be higher than 1nF. Considering the high complexity of the implementation of the FFT algorithm in a microcontroller, this method implies a higher computational load (and therefore power consumption) when compared to the charging time method.
Results and analysis
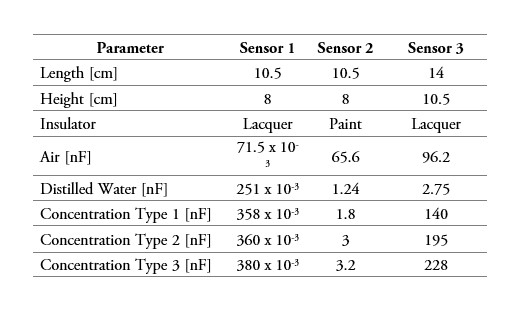
In total, 4 sensors were characterized. They shared the same size by pairs, only varying the insulation layer. For the test, a water container was designed aiming to limit the volume of the MUT. The characterization of the sensor involved the preparation of water samples with different salt concentrations, which in turn, will vary the sensor capacitance. According to results observed in table 2, it is possible to determine that, although the first sensor presents less sensitivity to the capacitance variation, it also shows better stability and the smallest equivalent impedance of all studied sensors.
Table 2
Capacitance value, using large sensors and varying insulating layer
Source: Own elaboration
Measurement Methods
When comparing both methods, we used an impedance analyzer to have an independent reference measurement. In the case of the time-based method, several samples are taken along the charging time interval, and later, the sample number is validated and multiplied by the time used to capture the voltage sample. A simple average is computed between the current sample and the previous one, aiming to mitigate external noise factors present in the ADC that might alter the charging curve. For the frequency-based approach, after computing the FFT of the signal generated by the oscillator, the microcontroller simply identifies the strongest component in the array, which corresponds to the oscillating frequency of the external circuit. Taking into account the LM555 design equations, it is a simple calculation to infer the capacitance value.
The experiments were divided in two sets: one for capacitors ranging 1-100nF and another for capacitors in the range of 100-700nF. figure 8(a) presents the relationship between our two methods (X-axis) and the impedance analyzer (Y-axis) for capacitor in the range of 1-100nF. The further the curve deviates from a unite slope line (slope m = 1), the higher the error of the obtained capacitance value. The error of the inferred values (when compared to the impedance analyzer) for both embedded methods in the microcontroller is also reported. From them, we can conclude that the time-based method (CT) is in general less precise when compared to the frequency-based method (FFT). This error is particularly higher for lower capacitance values, for which the CT technique has an error ten-times higher than that of the FFT technique. Figure 8(b) presents the second set of experiments for capacitors in the range of 100-700nF. As observed, the higher the capacitance range, the smaller the standard deviation tends to be, making them comparable. Nonetheless, the precision incurred by the time-based method was observed to be lower than the frequency-based error in general.
Another aspect to analyze in order to offer a comprehensive comparison between the two methods, is the execution time that the microcontroller incurs in the inference process. The execution time for the time-based technique is approximately 44µs, while the frequency-based approach requires 6.2ms. As observed, the capacitance charging time method is two orders of magnitude faster than the frequency domain approach. A longer and more computing intensive data processing algorithm, such as an embedded FFT, derives in a higher consume of energy, which is not a desirable trait in a portable device. On the other hand, the use of memory is smaller in the frequency domain method. To compute the FFT, a vector of 1024 positions is required to comply to the Nyquist criterion. At the same time, the time domain approach requires a vector of 3000 positions for the larger capacitors, in order to store enough voltage samples to compute the capacitance.
Additionally, it is worth mentioning that the charging curve method generates higher noise in measuring processes performed by the microcontroller ADC. This is the reason why the obtained value varies in a large range. Values reported are the result of an average of 20 experiments for each configuration. On contrary, the frequency domain method presents higher precision specially for small capacitances. The frequency domain method is also less sensitive to noise, and although it requires more computational resources, it seems more appropriate as measurement method in this application.
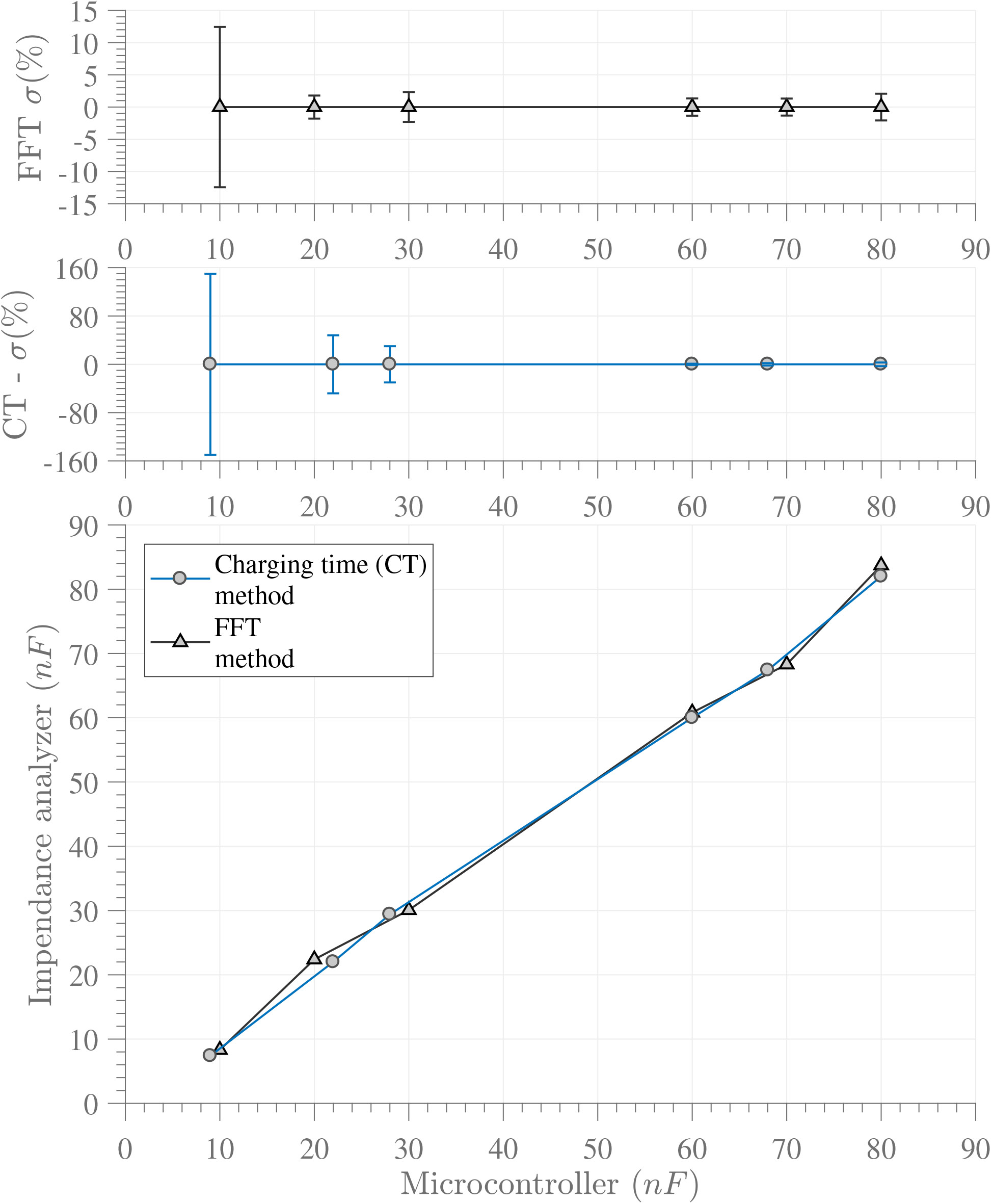 Figure 8
Measured capacitance value with the embedded techniques (charging time method-CT and frequency method-FFT) and an impedance analyzer. a) 1 − 100nF , b) 100 − 700nF
Figure 8
Measured capacitance value with the embedded techniques (charging time method-CT and frequency method-FFT) and an impedance analyzer. a) 1 − 100nF , b) 100 − 700nF
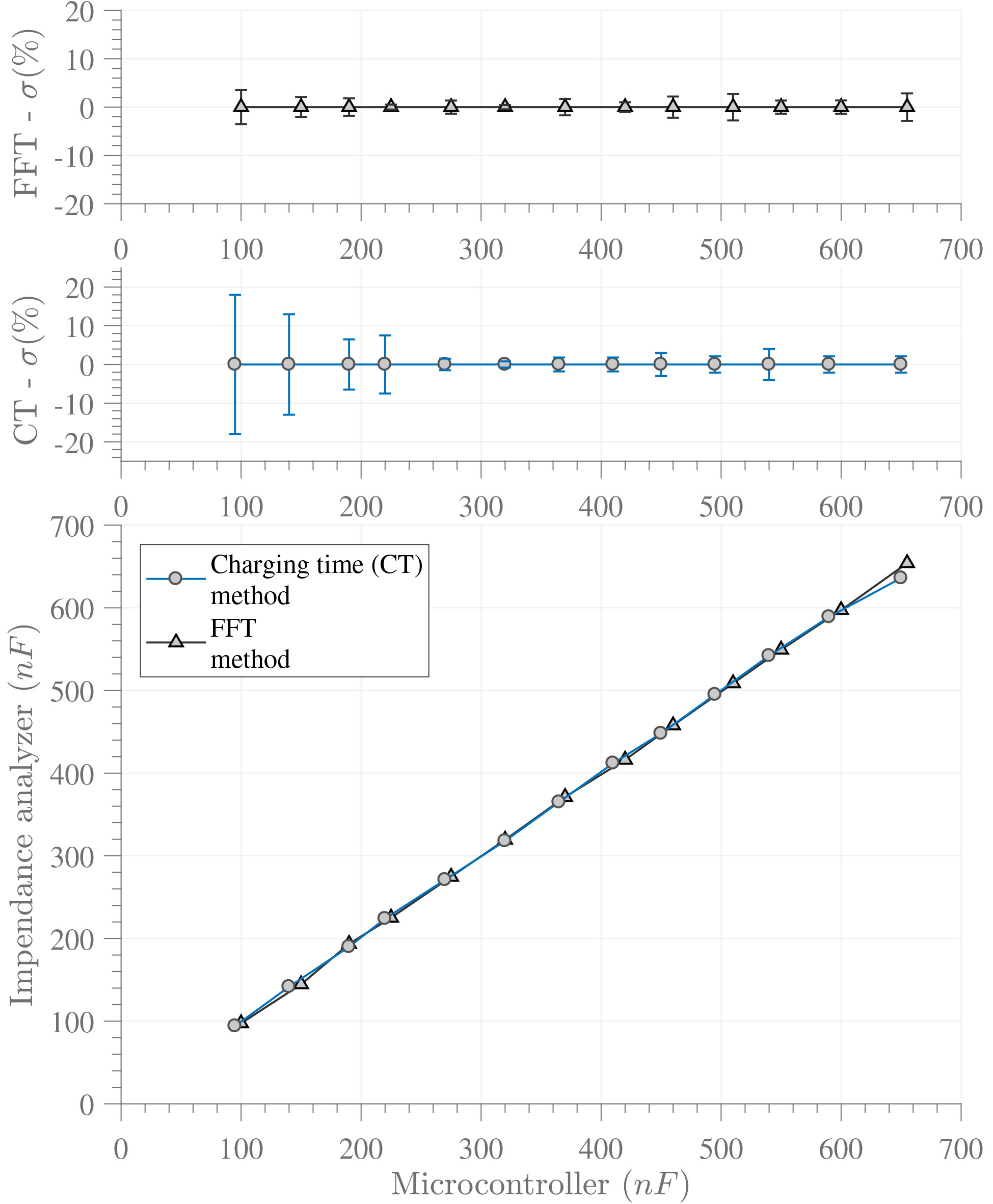
Source: Own elaboration
System Integration
The frequency domain approach was selected for the inference of the capacitance of the IDC sensor, and from the four analyzed sensors, the smaller one was selected and paint was used as the insulating coating layer, since it also presents higher stability, which in turn is a key trait when evaluating the associated capacitance of the sensor. The first stage of the system integration consisted in the sensor characterization to determine the measurement range of the system. For this, a verification of the oscillator frequency is required to guarantee a stable rate when it is connected to the IDC. Three types of water samples were used, corresponding to low, medium and high salt concentrations. table 3 presents the value of concentration of salt in [g/L] for the three different samples. It is possible to observe a small variation range on the variation of the capacitance from less than 1 nF to values higher than 1.62 nF. This small variation is the reason for the selection of the frequency domain method, which presents better resolution for small capacitance values. The results show that with this system, it is possible to differentiate between different pollution levels in the water.
Table 3
Capacitance value and detection accuracy, using large sensors and different concentrations
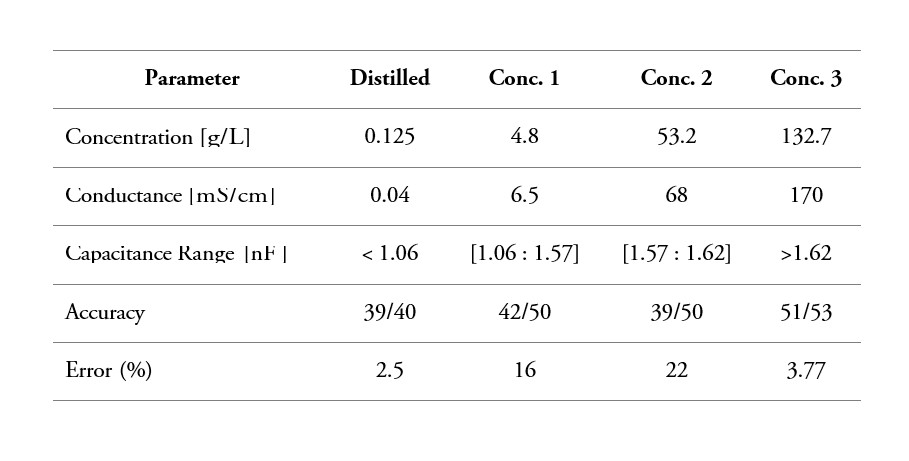
Source: Own elaboration
During the characterization, we observed a strong dependence on temperature. Several experiments showed that as the temperature changes, also does the capacitance. The following is the temperature setup for our experiments: room 18ºC ± 0.5, sensor 21.3ºC ± 0.3 and MUT of 19.1ºC ± 0.2. It is important to guarantee stable conditions during the experiments, and in addition, the sensor must be previously cleansed and completely submerged in the sample during the measurements. Each measure takes around 30-120 seconds. Another factor to be considered is the volume of water. For the experiments, the water volume was set to 240 ml, procuring that the surface of the sensor ended up completely covered by the fluid.
Table 3 also presents the error in the concentration of salt detected by the system. As observed, the system is capable of an adequate detection for distilled water and high concentration of salt, obtaining an error of 2.5% and 3.77% respectively. On the other hand, the percentage of error observed in low and medium concentration oscillates between 16% and 22%, being the medium concentration the more susceptible to be misclassified. The reason for this variation is attributed to the external factors such as the temperature that affects greatly the capacitance value, thus the computed conductivity of the water. A possible way to improve this would be for the system to acquire several samples and use the median of the values. The result of the water concentration classification, the obtained capacitance and the computed conductance, are then sent and stored in the Ubidots server for visualization purposes, where it is possible to observe a log of the sent information.
Conclusions and future work
We have proposed and implemented a low-cost monitoring system that integrates an IDC sensor with an embedded measuring technique enabling the in-site characterization of water samples without the need of expensive laboratory equipment. During the fabrication of the IDC heads, the insulation layer and the size were key factors. While the insulation layer reduces the sensor’s sensitivity, it also generates more stable readings. For the fabricated sensors, up to 6 layers of paint were used as insulation, however, these layers of paint are difficult to model in ANSYS and might be the reason for the error between the simulations and the characterization of the fabricated heads. While larger sensors generate a larger equivalent capacitance of the MUT, which is easier to measure, it also adds a larger and unknown equivalent resistance that affects the embedded measuring technique.
In terms of the embedded measuring techniques, the time-based approach is a very cheap technique (only one external resistor) to measure the capacitance values. On the other hand, although the FFT approach requires more computational resources and a simple external circuit, it provides more accurate measurements in a wider range of capacitances (1-700nF). Our tests show that the proposed system, a combination of an IDC and an embedded measuring technique, is capable of distinguishing between clean water and 3 levels of concentration of a contaminant. The results also validate the proposed monitoring paradigm of having a massive number of low-cost sensors to have a wide, but not highly accurate, view of the status of the hydrological resources of a region. With this information, the corresponding protection agency can plan the more accurate and expensive monitoring campaigns only for the areas with a suspicious behavior.
As part of our ongoing and future work, we are expanding the cloud-based platform to receive readings from multiple sensors, while also integrating a visualization platform to properly present the status of the region of interest. Since IDC sensors are highly dependent on external factors, such as the temperature, we will include a set of temperature sensors to be able to correct the acquired values.
References
[1] IDEAM, Hoja metodológica del indicador Índice de calidad del agua, Bogotá: Colombia: IDEAM, 2011.
[2] D. A. Sanz, E. A. Unigarro, J. F. Osma, & F. Segura-Quijano, “Low cost wireless passive microsensors for the detection of hazardous compounds in water systems for control and monitoring,” Sensors and Actuators, B: Chemical, vol. 178, pp. 26-33, 2013. https://doi.org/10.1016/j.snb.2012.12.027
[3] C. Veyres & V. Fouad Hanna, “Extension of the application of conformal mapping techniques to coplanar lines with finite dimensions,” International Journal of Electronics, vol. 48, no. 1, pp. 47-56, 1980.
[4] A. V. Mamishev, K. Sundara-Rajan, F. Yang, Y. Du, & M. Zahn, “Interdigital sensors and transducers,” in Proceedings of the IEEE, vol. 92, no. 5, 2004, pp. 808-844.
[5] J. W. Kim, P. Pasupathy, S. Zhang, & D. Neikirk, “Measurement of liquid complex dielectric constants using non-contact sensors,” IEEE Sensors, pp. 2017-2020, 2009. https://doi.org/10.1109/ICSENS.2009.5398291.
[6] J. W. Kim, Development of Interdigitated Capacitor Sensors for Direct and Wireless Measurements of the Dielectric Properties of Liquids, Ph.D. dissertation, The University of Texas at Austin, United States, 2008.
[7] N. Angkawisittpan & T. Manasri, “Determination of Sugar Content in Sugar Solutions using Interdigital Capacitor Sensor,” Measurement Science Review, vol. 12, no. 1, pp. 8-13, 2012. https://doi.org/10.2478/v10048-012-0002-0
[8] U. Kaatze, “Measuring the dielectric properties of materials. Ninety-year development from low-frequency techniques to broadband spectroscopy and high-frequency imaging,” Measurement Science and Technology, vol. 24, no. 1, pp. 1-31, 2013. https://doi.org/10.1088/0957-0233/24/1/012005
[9] A. P. Gregory & R. N. Clarke, “A Review of RF and Microwave Techniques for Dielectric Measurements on Polar Liquids,” IEEE Transactions on Dielectrics and Electrical Insulation, vol. 13, no. 4, pp. 727-743, 2006.
[10] S. Zhang, Interdigitated Capacitor Sensor for Complex Dielectric Constant Sensing by, Ph.D. dissertation, The University of Texas at Austin, United States, 2010.
[11] L. Yonghong & H. Yunzhi, “Application of Interdigital Capacitive Sensors for Detecting Power Cable Insulation Damage,” in IEEE International Conference on Mechatronics and Automation (ICMA), vol. 1, 2015, pp. 1795-1799.
[12] J. Wang et al., “Rapid Determination of Meat Moisture Content Using Radio-Frequency Dielectric Measurement,” IEEE Access, vol. 6, pp. 51384-51391, 2018. https://doi.org/10.1109/ACCESS.2018.2864308
[13] W. Hafiy et al., “Inter-Digital sensor for non-invasive blood glucose monitoring,” in 2018 IEEE International Conference on Innovative Research and Development (ICIRD), no. May, 2018, pp. 1-6.
[14] X. Wang et al., “Mechanism and Experiment of Planar Electrode Sensors in Water Pollutant Measurement,” IEEE Transactions on Instrumentation and Measurement, vol. 64, no. 2, pp. 516-523, 2015. https://doi.org/10.1109/TIM.2014.2340641
[15] A. Azmi, A. A. Azman, K. K. Kaman, S. Ibrahim, S. C. Mukhopadhyay, & S. W. Nawawi, “Performance of Coating Materials on Planar Electromagnetic Sensing Array to Detect Water Contamination,” IEEE Sensors Journal, vol. 17, no. 16, pp. 5244-5251, 2017. https://doi.org/10.1109/JSEN.2017.2720701
[16] O. Martens, S. Pille, & M. Reidla, “Capacitance Measurement with MSP430 Microcontrollers,” in 2014 6th European Embedded Design in Education and Research Conference (EDERC), 2014, pp. 260-263.
[17] O. Casas, “Calibration-less direct capacitor-to- microcontroller interface,” Electronics Letters, vol. 52, no. 4, pp. 289-291, 2016. https://doi.org/10.1049/el.2015.3706
[18] L. Bengtsson, “Direct analog-to-microcontroller interfacing,” Sensors and Actuators, A: Physical, vol. 179, pp. 105-113, 2012. https://doi.org/10.1016/j.sna.2012.02.048
[19] S. Malik, K. Kishore, T. Islam, Z. H. Zargar, & S. Akbar, “A time domain bridge-based impedance measurement technique for wide-range lossy capacitive sensors,” Sensors and Actuators A: Physical, vol. 234, pp. 248-262, 2015. https://doi.org/10.1016/j.sna.2015.09.007
[20] E. Serrano-Finetti, O. Lopez-Lapeña, & O. Casas, “Calibration-less direct capacitor-to-microcontroller interface,” Electronics Letters, vol. 52, no. 4, pp. 289-291, 2016. https://doi.org/10.1049/el.2015.3706
Notes
*
Research paper
1
Ubidots. See https://www.ubidots.com.
Author notes
a Corresponding author. E-mail: diego-mendez@javeriana.edu.co
Additional information
How to cite this article:: D. Mendez, M. Pérez, A. Farfan, and E. Gerlein, “IDC Sensor for low-cost water quality monitoring applications,” Ing. Univ., vol. 26, 2022 [Online]. https://doi.org/10.11144/Javeriana.iued26.islc


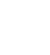
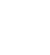
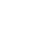
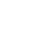







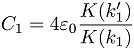 (1)
(1)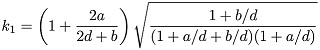 (2)
(2)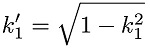 (3)
(3) (4)
(4) (5)
(5) (6)
(6)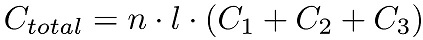 (7)
(7)




 (8)
(8)
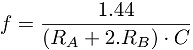 (9)
(9)



