Introduction
The blood supply chain is aimed at providing blood products for hospitals. The most important blood products are red blood cells, platelets, plasma, and cryoprecipitate. These products are mainly used in medical treatments. Each product has different shelf life being platelets the most critical with only five days after production. Given this, decisions on inventory for blood products are highly critical. On the one hand, if blood is collected in large quantities, it can get expired. On the other hand, if blood is collected in small quantities, the risk of stockouts is increased. Reviews on the different models applied to the blood supply chain can be found in [1], [2], and [3].
Different inventory policies have been proposed in order to deal with perishable products. However, this continues to be an active research field. Different methodologies have been proposed in the blood supply chain to improve indicators such as the number of expired units, number of stockouts, and cost. However, most of them are focused on using simulation to define good inventory policies.
Inventory policies for blood platelets are also usually studied for single hospitals without considering the relationship with the blood center and other hospitals. This can increase the number of expired units and stockouts since decisions are not made considering the whole system.
Different approaches have been used to study the platelet inventory problem. However, given the complexity of the problem, one of the most used methodologies is simulation. One of the main concerns in simulation is experimentation to obtain optimal parameters. Hence, is necessary to combine optimization techniques to find good solutions to complex problems. The integration between simulation and optimization can be carried out in different ways [4]. One of the methods to combine simulation and optimization is called "simulation-based optimization." This method has been employed to generate optimal solutions for problems in different areas such as construction [5], production planning [6], and healthcare [7].
This paper proposes a simulation-based optimization algorithm that uses a Vendor-Managed inventory approach to solve the blood platelets distribution and production problem. The proposed model aims to make optimal (or near-optimal) decisions on inventory policies for blood centers and hospitals under a Vendor-Managed inventory approach. The model is tested, and the results show that the proposed methodology can improve the total operational cost of the system and the number of expired units for both hospitals and blood centers while service levels are kept. The proposed model considers several echelons of the blood supply chain, including production, inventory, and distribution.
This paper proceeds as follows: Firstly, the literature review of the main concepts used in this paper is presented. Then, the problem and the type of decisions to be studied are described. After this, we present the algorithms used and the integrated methodology proposed. In addition, the results applying of the proposed model and methodology to a case study are explained, and finally, the main conclusions and extensions of this work are mentioned.
Literature Review
Inventory of platelets
The majority of the literature on the blood supply chain concerns the inventory stage. However, most of it is focused on Red Blood Cells. Recently inventory research has focused on platelet concentrates. This section shows how the platelets inventory problem has been addressed previously.
Different features such as breaks and several types of demand have been considered. [8] develop a Markovian model to represent decisions on production and inventories of platelets. The model includes multiple periods as well as weekend breaks. Ordering, shortages, and production are integrated into a general cost function to be optimized. This article considers two types of demand and different issuing policies to meet them as well as order-up-to policies. Furthermore, [9] and [10] present articles based on the same model. The first paper includes Christmas, New Year, and Easter breaks. The second paper uses the model to introduce changes and study different scenarios. The scenarios studied by the authors consider differentiation of blood types and changes in shelf life, as well as the crossmatch (the process of checking that the recipient’s blood is compatible with the donated blood) ratio and issuing policies (the process of deciding which blood units will be issued).
Several methodologies, including simplified methods, analytical models, and combined methods have been proposed to study inventory decisions for blood platelets. [11] present a simplified methodology for ordering platelets based on service levels. The authors also discuss the convenience of using cost as an objective for platelet inventory policies. Furthermore, [12] present an analytical model to define optimal inventory policies for platelets. The model extends analytical policies to three periods and includes different replenishment modes, such as standard and optional. Finally,[13] and [14] propose a combination of methodologies. The first paper uses the newsvendor problem, linear programming, and approximation dynamic programming to address the platelets inventory problem. The second paper uses a hybrid simulation optimization model to study inventory decisions for platelets considering age and stochastic demand.
Finally, other authors have modelled the problem as a Markov Decision Process. [15] consider a discrete-time inventory system for a perishable product where demand exists for products of different ages. The authors propose a simple inventory replenishment and allocation heuristic to minimize the expected total cost over an infinite time horizon. The problem is modeled as a Markov Decision Process (MDP), derives the costs of our heuristic policy, and computationally compares this policy to extant “near-optimal” policies in the literature. Recently, [16]illustrated how MDP or Stochastic Dynamic Programming (SDP) could be used for blood management at blood banks. The state space is too large to solve most practical problems using SDP. Nevertheless, an SDP approach is still argued and shown to be most helpful in combination with simulation. An optimal policy is derived by SDP. Results show how outdating, or product waste of blood platelets can be reduced from over 15% to 1% or even less while maintaining shortage at a very low level.
This paper contributes in different ways to the platelets inventory field. Firstly, we considered the vendor management problem; simultaneously; we analyzed the whole system. We considered blood center inventory policies and hospital policies in a centralized decision-making system. In addition, we also consider production decisions, in other words, how many platelets should be produced to serve demand. None of these aspects have been considered previously at the same time for the platelets inventory problem.
Simulation-Based Optimization applied to Vendor-Managed Inventory Problems
Simulation-based optimization has shown to be an effective methodology for addressing general inventory problems. Multiple applications can be found in [17]. However, for the Vendor-Managed Inventory Problem, the number of applications found is lower.
Metaheuristics are one of the most used methodologies to solve the VMI problem. [18] presents a simulation optimization model to study the vendor management inventory problem. The paper aims to analyze the relations between GA parameters and optimal solutions. This article compares several combinations of GA parameters, the effects on optimal solutions, and the time to reach optimal solutions. Furthermore, [19] developed a hybrid algorithm based on genetic algorithm (GA) and particle swarm optimization (PSO) to maximize inventory turnover along with the constraint of lack or shortage of goods in the production lines. The model also considers minimum and maximum inventory constraints in the warehouse of the producer. Finally, [20] developed a simulation-optimization approach to study a problem related to replenishing inventories at retailers in distribution networks operated under the paradigm of Vendor-Managed Inventory (VMI). The authors argue that many factors such as random variables and many costs make the problem complex. The authors point out that these factors are usually simplified in the literature. Furthermore, the proposed heuristic based on simulated annealing combined with discrete event simulation can include these factors presenting a better performance than other heuristics.
Exact methods have also been used for the VMI Problem. [21] develop a decomposition algorithm to study a Vendor-Managed inventory problem for blood products. This article is based on a case study from China, and it is aimed at optimizing the blood product scheduling scheme by constructing a Vendor-Managed inventory routing problem (VMIRP). The proposed model also balances the supply and demand such that the relevant operational cost is minimized. In addition, [22] designed a dynamic VMI system. In this system, the entire supply chain performance is optimized. This includes production planning, distribution strategy, and inventory management. The VMI system is modeled as a mixed-integer linear program (MILP) using discrete-time representation. The authors explore different solution methodologies. Finally, a rolling horizon approach that simultaneously combines the aggregate and the detailed models is designed to solve the problem.
This paper contains several aspects different from the reviewed papers in terms of methodology. Firstly, we applied the simulation optimization methodology to propose a VMI methodology for the most critical blood product, platelets. Secondly, we also include production decisions as well as the typical dispatching decisions in the VMI problem.
Problem Definition
Context
In general terms, the supply chain management of human blood products is highly complex. Blood products, especially platelets, have short lifespans (about five days). Hence, production and distribution scheduling is a costly and time-consuming operation for blood banks. These institutions have two major concerns. In any given period, if demand is overestimated, most of the production scheduled will go to waste, increasing operational costs without any additional contribution to end-users of the product. On the other hand, if demand is underestimated, there will be a shortage of platelets across all related hospitals, potentially endangering the lives of a significant number of patients.
Although both problems pose a significant challenge to the supply chain, it is by far more critical to be able to respond to existing demand. The problem becomes even more complex when multiple hospitals or medical centers with different demand distributions depend on the same donor center supplies. Because of this, the whole problem can be summarized into two critical decisions that blood centers must take. The first one is about how many platelets to produce, given the current size of the donor pool and demand estimates. The second one is how much and where to send the existing inventory to minimize the previously mentioned variables (expired platelets and stock-outs). Neither of these decisions are trivial. Human blood is transformed and separated into its basic constituents (platelets among these) using a process called blood fractionation, usually performed by centrifuging the blood. This process is carried out using specially designed blood bags, which can be single, double, triple, or quadruple. Only the last two (the most expensive ones) can be used to extract platelets, so the donor center must know how many of these bags to use in the total donor pool. Similar problems have been explored in the literature using non-collaborative strategies. In this paper, we propose to model the system as a particular case of a Vendor-Managed Inventory System, where a centralized blood bank schedules production and shipping to several hospitals needing platelets.
Vendor-Managed Inventory
In traditional non-collaborative systems, suppliers limit their functions to deliver customer orders to the best of their capacity. In contrast, in Vendor-Managed inventory environments, suppliers have a much more relevant role in the operation of the supply chain. They are responsible for defining how much product needs to be sent to each customer. This planning is performed using relevant information like inventories and sales. As a result, these systems often come with a tight information system coupling between clients and vendors, so the information is always readily available. In this paper, we propose using a VMI methodology to reduce the general levels of stock-outs and expired products in the blood supply chain, more specifically, the platelets supply chain.
Why Simulation-Based Optimization
With the VMI model introduced and assuming that in the proposed system, the blood bank has instant access to inventory and past sales information from every hospital, a way to define optimal or near-optimal supply management policies is needed. Considering that demand and supply are stochastic and seasonal in the blood supply chain and platelets are highly perishable, estimating optimal inventory policies is not a trivial task. Because of this, robust methodologies such as simulation-based optimization are required to improve the system’s performance in terms of the considered factors (which will be discussed later).
Methodology
The methodology proposed in this paper is based upon two major techniques used in Operations Research: simulation and optimization. According to [4], These two techniques can be integrated into several ways. In this paper, we used an integration methodology called "Simulation-Based Optimization," where a complete simulation run is carried out during each iteration of the optimization process [4].
In the described problem, simulation is used to evaluate the performance of a given solution provided by a genetic algorithm procedure. On the other hand, the genetic algorithm obtains optimal or near-optimal solutions.
It is important to clarify that the definition of optimality in a simulation environment is different from the one in a deterministic optimization environment. In a simulation, we can find optimal solutions according to the samples generated and the different runs of the simulation model. This way we can provide conclusions on the optimality considering confidence intervals. However, this is different from an optimal solution for a deterministic problem where we are sure that there is no better solution.
The genetic algorithm’s fitness function is the average result of the simulation model metrics. Hence, for each individual of the genetic algorithm, a simulation model run is carried out. The final result of the integrated simulation-based optimization model is an optimal or nearly optimal solution to the described inventory problem. Figure 1 shows the proposed methodology, along with its inputs, outputs, and internal mechanics.
The process developed in each stage is detailed in the following sections.
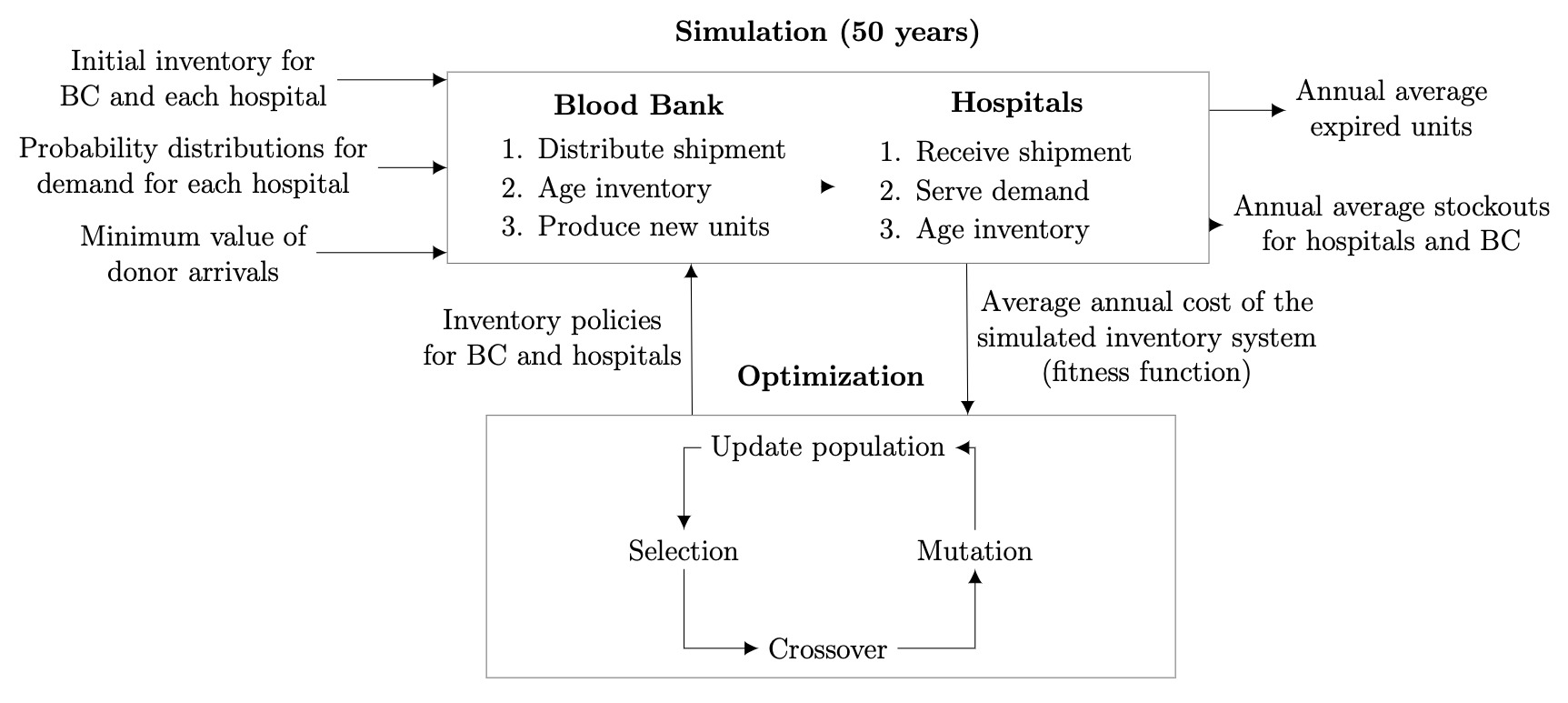 Figure 1.
General methodology
Figure 1.
General methodology
BC: Blood center, used interchangeably with Blood bank
Own Source
Simulation model
Simulation evaluates how well the system performs under a certain inventory policy. In order to develop the simulation process, it is necessary to define several aspects, such as the type of inventory system and the logic of the inventory model in hospitals and blood centers.
Inventory System
Periodic inventory models (usually called order up-to policies) are commonly used in the blood supply chain since health staff can easily operate them. This model relies on two main parameters R and S. R defines how often the inventory level is revised, and S defines the order up to quantity in every revision. It is important to highlight that the described blood supply chain needs several inventory policies (at least one for each hospital). The simulation model represents the system’s daily operation using pre-defined inventory policies for each hospital. This process is repeated for 50 years to generate a yearly average for the key performance indicators of the system.
The pre-defined inventory policies are provided by the optimization model described in Optimization model described later.
Inventory logic
We propose a realistic inventory logic to simulate the previously described inventory model. First, the system will be modeled in one-day intervals, as this time frame is enough to represent the actions to be modelled without adding unnecessary computational overhead.
Both the distribution center and hospitals will plan inventory replenishment using the periodic inventory model described above, with revision periods of 1 day. Each actor in the system has its order-up-to quantity. The process of simulating a single day can be summarized as follows:
-
The distribution center will review orders placed the previous day.
-
Based on its internal inventory state and the heuristic defined in 4.2, the distribution center plans the shipments to each hospital and dispatches them. All shipments are discounted from the distribution center's inventory in a FIFO manner.
-
Each hospital receives the shipment from the distribution center. Demands are generated.
-
Hospitals serve demand using existing inventory plus the fresh shipments from the blood bank.
-
Stock-outed units are calculated for each hospital.
-
Inventory for all entities is aged (each platelet unit is now a day closer to expiration). It is important to remember that the inventory for each entity cannot be represented as a single number but as five (one quantity for each expiration state). The aging process can mathematically be expressed as presented in equation (1):
where: I t,i
Platelets that are i days from expiration on day t
H= Number of hospitals in the system
Following this calculation, all It,0's are counted as expired.
-
7. Based on their final inventory and their order-up-to policies, each hospital places an order for platelets for the next day.
-
8. Based on its final inventory and order-up-to policy, the blood bank defines the production level for the next day (the number of fresh platelets that will enter the system the next day).
-
9. All stock-outed and expired units are recorded. It is important to note that differences between hospital orders and blood bank shipments are counted as stock-outs too.
Inventory Heuristic
Two things were considered to distribute available inventory among all hospitals: one, the actual orders of each hospital and the sum of the available inventory to send. The heuristic is simple yet powerful. All orders are fulfilled if the sum of orders is lower or equal to the available inventory. In the opposite case, we calculate the maximum level of orders that can be fulfilled with a simple proportion between the total orders and the total inventory as presented in equation (2):
where:
α = Maximum service level
O
t = Sum of all orders
It= Total inventory available
With this α alone, we could already compute what each shipment will be in that particular case. However, to allow the optimization algorithm to take part in this heuristic, we added a trainable parameter that could influence the distribution outcome. This parameter is used to control the actual service level for each heuristic run. Equation 3 below clarifies this process.
where:
Si = Shipment size to the i-th hospital
α = Maximum service level
ω = Trainable heuristic parameter
Oi = Platelet order of the i-th hospital
H = Number of hospitals in the system
Because this parameter is used as a percentage, it is guaranteed that the quotient with 100 is always between 0 and 1. Details on the nature of this ω parameter are described in the solution encoding section.
Optimization model
The solutions evaluated by the simulation model are obtained by an optimization procedure developed by a genetic algorithm. This algorithm aims at finding optimal inventory policies for both the blood center and the hospitals. Different constraints such as maximum production level and maximum order up-to level are encoded in the defined chromosome. The fitness function defines the inventory system’s total cost, including blood centers and hospitals. This algorithm interacts with the simulation model until solutions converge to optimal or near-optimal values.
The proposed methodology does not consider a defined planning horizon. Instead, the model aims to provide a general inventory and distribution policy that could theoretically be used in any system state. The simulation model's sole purpose is to estimate the performance of the optimized policy in each generation of the genetic algorithm.
Solution encoding
Each individual in the optimization process may be encoded as an integer-valued vector for this particular problem. A more detailed explanation follows.
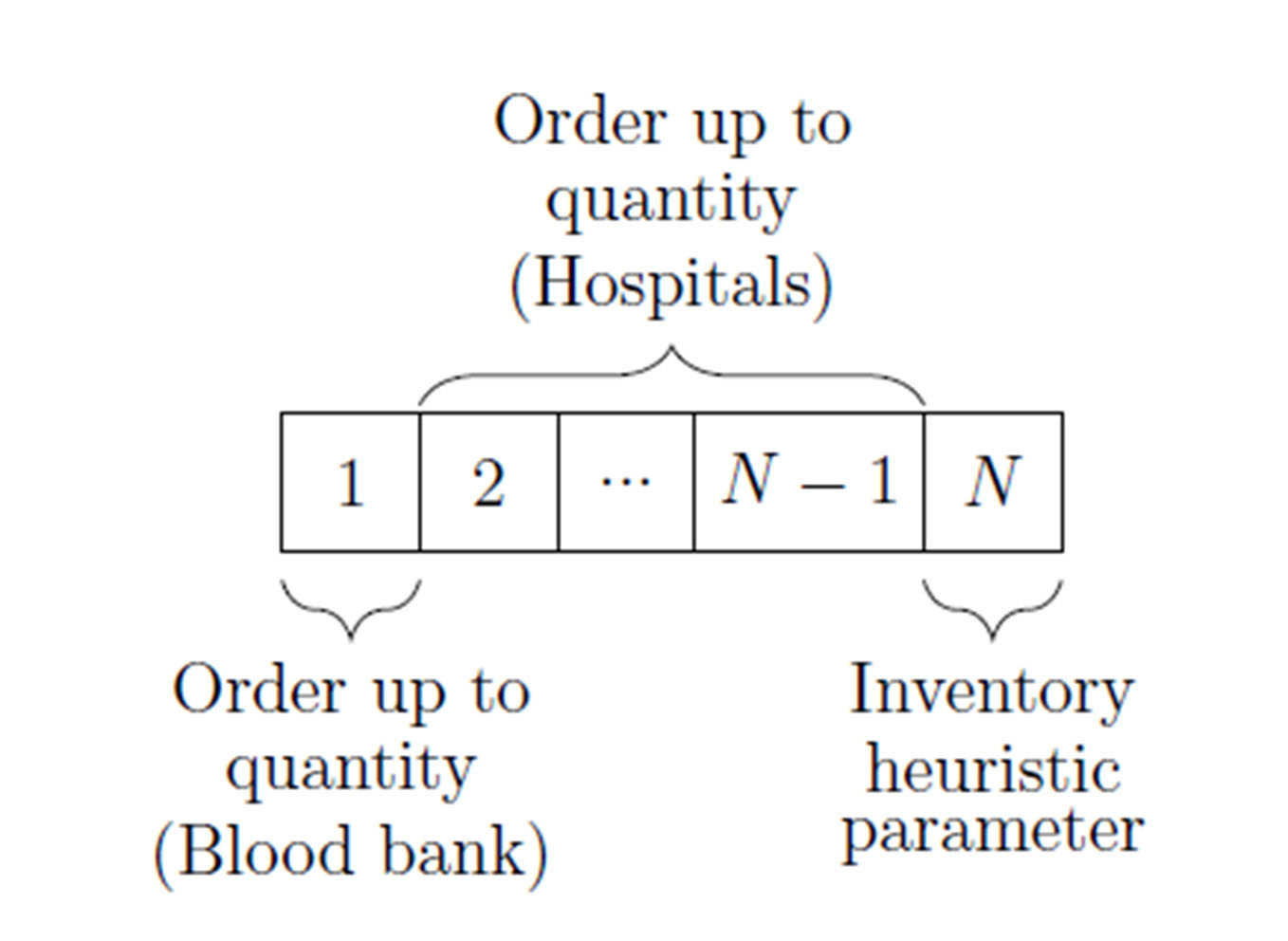 Figure 2
Individual encoding for genetic algorithm
Figure 2
Individual encoding for genetic algorithm
Own source
Position 1:
Order up-to level for the blood bank (S). In each step, the blood bank will schedule a production order for platelets to reach this number the next day. With the current donation distribution, it is guaranteed that the production order will be fulfilled 100 % of the time (this means that the maximum value of S will be the minimum recorded donation size in recent history).
Position 2 to N-1
Order up-to-level for each hospital (S). Each time step, hospitals will issue an order to the blood bank to maintain this inventory level. Hospital orders may or may not be fulfilled based on the blood bank inventory levels.
Position N:
This parameter will define the behavior of the inventory logic that should be used when the blood bank does not have enough platelet units to fulfill all orders from hospitals and medical centers. The detailed behavior of this heuristic is fully defined in 4.2.
The vector’s length will depend on the number of hospitals and medical centers to be simulated in the system.
Fitness function
In order to define a fitness function that properly measures how well solutions perform, we decided to consider both expired units and stock-outs. Nevertheless, it is essential to highlight that they should have different costs in the fitness function. The total of expired units is an important indicator since blood is obtained from altruistic donors and processing the raw blood into platelets has a considerable cost. However, total stock-outs and, more generally, the service level are more concerning in blood supply chains since many medical procedures depend on the platelets’ availability. Because of this, we propose different costs for both metrics (expired units and stock-outs).
It should be noted that the cost for expired units in hospitals is different from to cost of expired units in the blood center. This is because that platelets in hospitals include additional transportation and handling costs. Hence, they should be weighted differently, presumably with a higher cost.
The equation that represents the fitness function can be expressed as follows:
Where:
Sst = Yearly average of the sum of stockouts in the system
Hexp = Yearly average of the sum of expired units for all hospitals
BBexp = Yearly average of the expired units in the blood bank
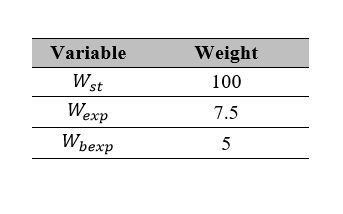
Wst = Weight for system stock-outs
Wexp = Weight for hospital expired units
Wbexp = Weight for blood bank expired units
In order to estimate this performance, each policy (one for each individual in the GA) is simulated 50 times (one year long each). After this, variables Sst, Hexp, and BBexp are the resultof the average of the sums of stockouts, expired units inside the hospital, and expired units inside the blood bank, respectively, across the 50 simulation iterations.
Genetic algorithm operators and solution framework
The proposed genetic algorithm was codified and solved using the computational framework DEAP [23]. The genetic algorithm operators used are defined as follows:
-
Selection - Tournament: This selection operator takes n random individuals from the population and chooses the best among them. This selection is performed k times.
-
Crossover - Two-point crossover: This operator performs a two-point crossover merge between two individual chromosomes.
-
Mutation - Uniformly random: This function assigns a new value to each property of an individual with probability α The new property value is defined by Uniform (a, b)
-
Fitness Function - defined by Equation 4.
We invite the reader to review DEAP documentation for further illustration [24].
The parameters for each operator were obtained by experimentation and are presented in the case study section.
Case Study
System definition
In order to provide a concrete model to test the defined framework, we propose a system with a distribution center (blood bank) and four (4) dependent hospitals. Different parameters such as demand probability distributions, size, and scale of the hospital, and parameters for the execution of the genetic algorithm need to be defined.
In the blood supply chain, demand usually has different behaviors depending on the day of the week. Hence, it is necessary to define a probability distribution per day per hospital. Table 1 presents the parameters for the probability distributions for each day. These parameters are inspired by the information presented in [25], which includes detailed information about the probability distributions for each product for each day as well as donor arrival distributions for each day.
The information used in[25] was obtained from the Hemocentro Distrital in Bogota, Colombia, from July 2013 to June 2014.
Table 1.
Demand distribution parameters for each day of the weak
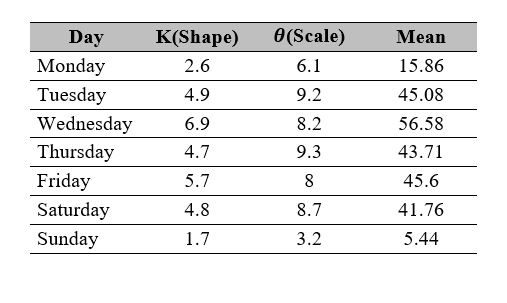
adapted from [25]
To represent different hospital sizes, we introduced and additional parameter that serves to scale the demand, the parameter for each hospital can be found in Table 2.
Table 2
Demand scaling factors for each hospital
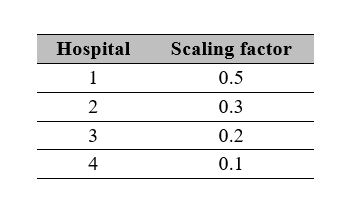
Own source
Another critical factor to note is the availability of blood to obtain platelets. To simplify the analysis, we assume a fixed daily number of donors (the chosen value of 100 is lower than the actual number of donors for each day for the system’ historical data).
It is also important to define parameters used in the fitness function according to Equation 4; the assigned weights are defined according to Table 3.
Table 3.
Fitness function weights.
Own Source
Results
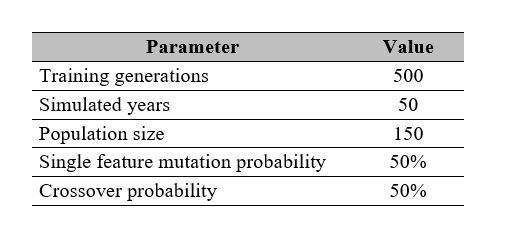
Parameters for training
Before the training process can start, parameters have to be defined. The selection of parameters is dependent on the nature of the problem and is always subject to improvement and possible constraints. For the case study, the selected parameters are defined in Table 4.
Table 4.
Training parameters
Own source
Training Results
With the model, methodology, and training parameters fully defined, the genetic algorithm was run over the defined 500 iterations. Figure 3 shows the training progression of the, plotting the best fitness value found at each generation.
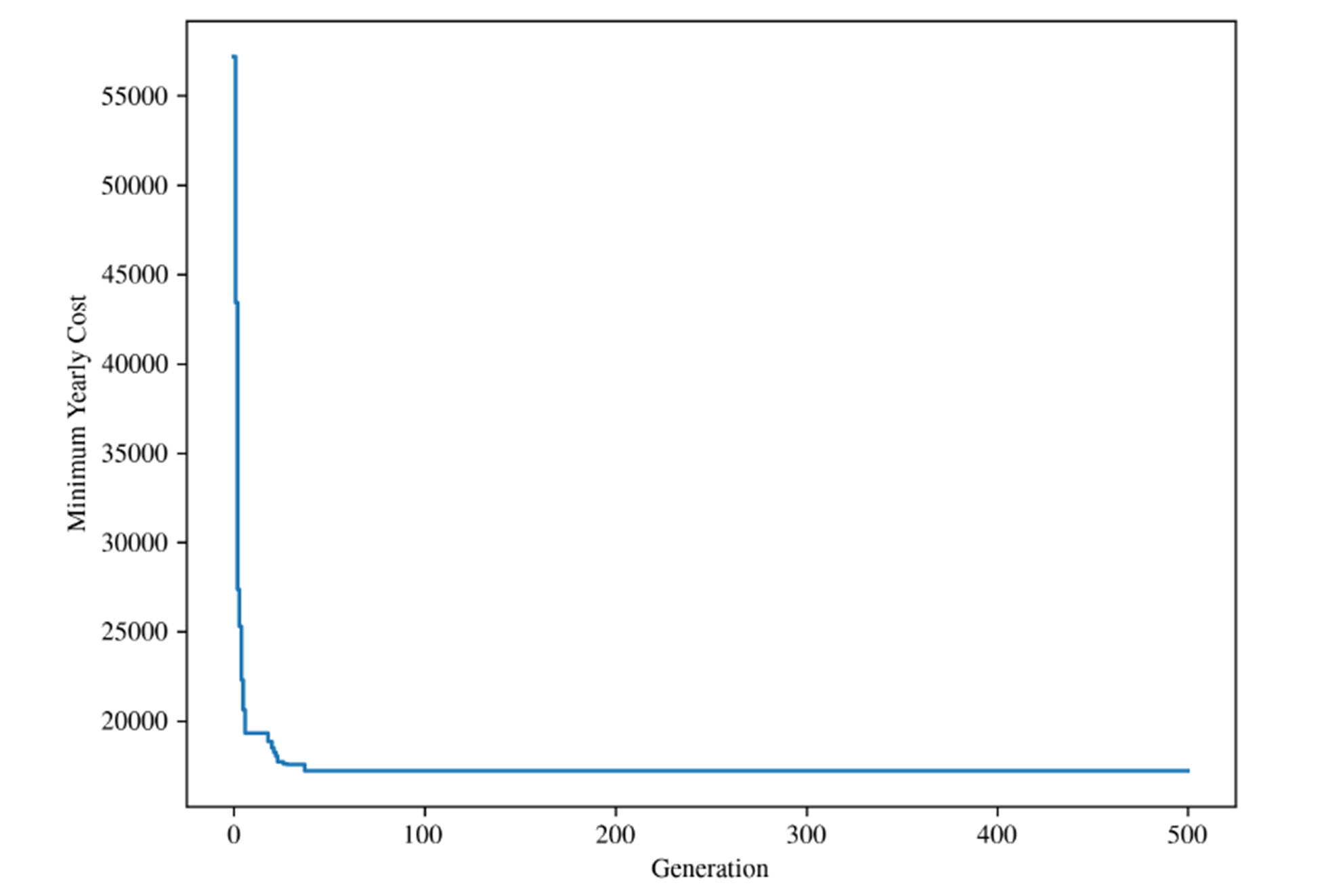 Figure 3.
Training Progression Plot
Figure 3.
Training Progression Plot
Own Source
Figure 4 depicts the best solution reported by the genetic algorithm after 500 generations of evolution.
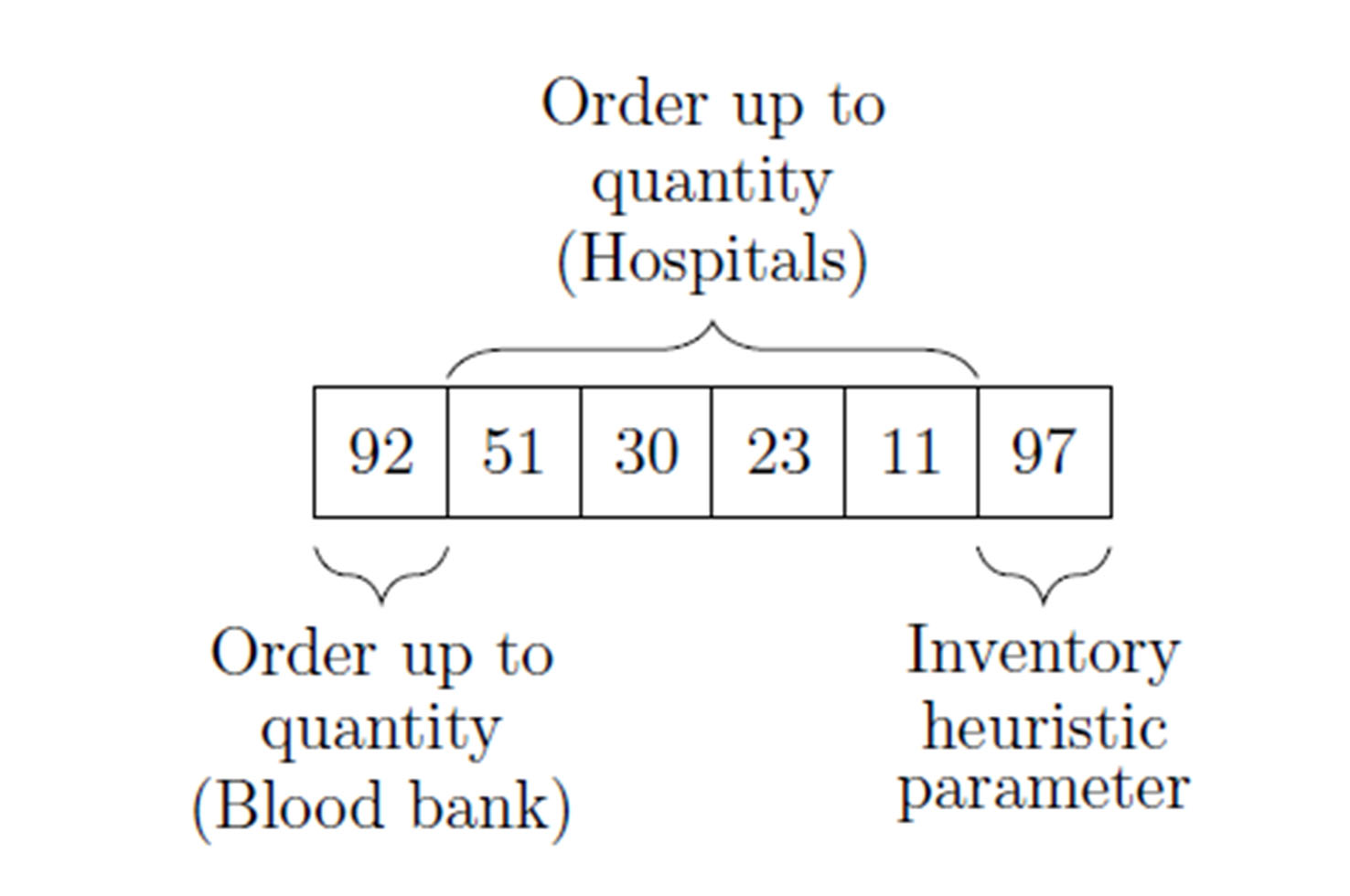 Figure 4.
VMI Presumed Optimal Solution
Figure 4.
VMI Presumed Optimal Solution
Own Source
To study the performance of the proposed methodology, we propose to compare the solution found with a solution obtained through the same simulation-based optimization process but without the benefits of the VMI implementation. These two solutions will be bench-marked, taking all relevant metrics into account, especially the total cost of operation and general service level. A summary of all considered metrics can be found in Table 5.
Table 5.
Results summary
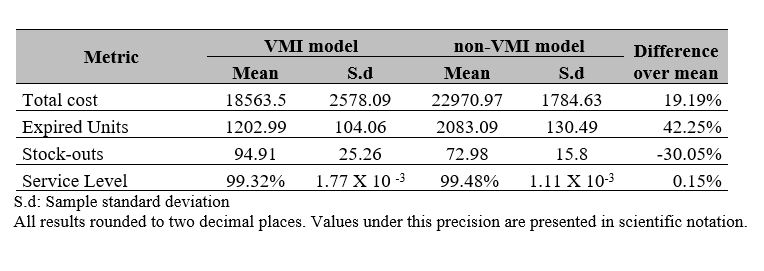
S.d: Sample standard deviation
All results rounded to two decimal places. Values under this precision are presented in scientific notation.
Own Source
This new comparison solution will be generated using the same methodology described above, but each parameter will be optimized separately. It is relevant to mention that every hospital optimizes its order-up-to parameter under the assumption that the totality of ordered platelets will be delivered.
Figure 5 describes the solution found using this method.
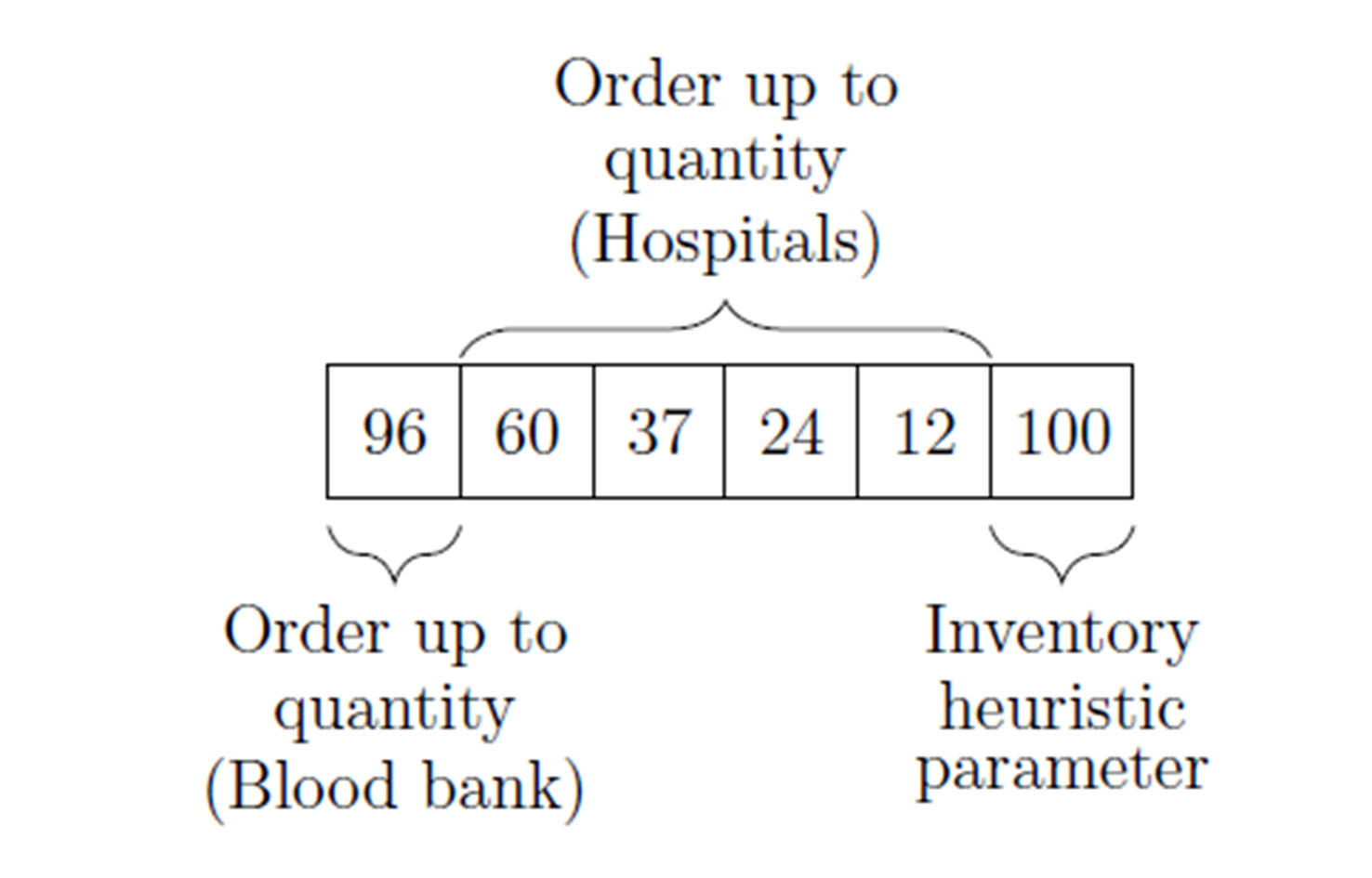 Figure 5.
Non-VMI Presumed Optimal Solution
Figure 5.
Non-VMI Presumed Optimal Solution
Own Source
In order to provide statistically significant conclusions, 2500 years (this is 2500 one-year long iterations, each iteration run with the same initial conditions to avoid correlated data) will be simulated with each solution.
In Figure 6, we can observe the behavior of the simulation results in terms of the total cost as defined by the fitness function of the genetic algorithm. The VMI approach averaged its yearly cost to 18563.50, with a standard deviation of 2578.09, while the non-VMI model presented 22970.97 and 1784.63, respectively. In this aspect, the VMI model shows a 19.19% advantage over the non-VMI solution.
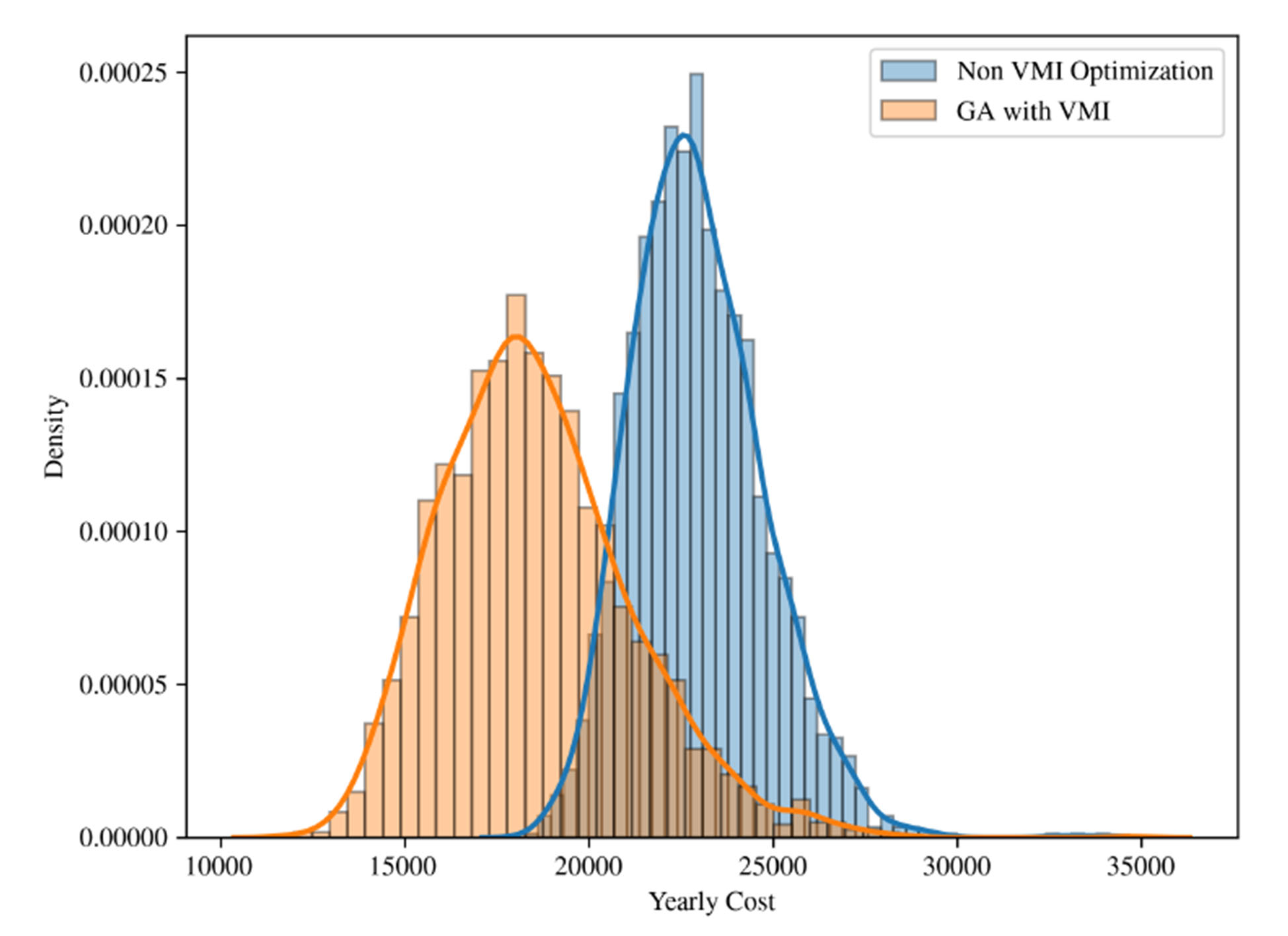 Figure 6.
Yearly Cost Comparison
Figure 6.
Yearly Cost Comparison
Own Source
In terms of expired units, the results are even more divergent. The VMI solution averaged 1202.99 expired units every year, with a standard deviation of 104.06; in contrast, the non-VMI model-averaged 2083.09 with a standard deviation of 130.49. In this scenario, the VMI solution provides a 42.25% reduction. As shown in Figure 7, even the highest count from the VMI model is lower than the lowest one from the non-VMI model.
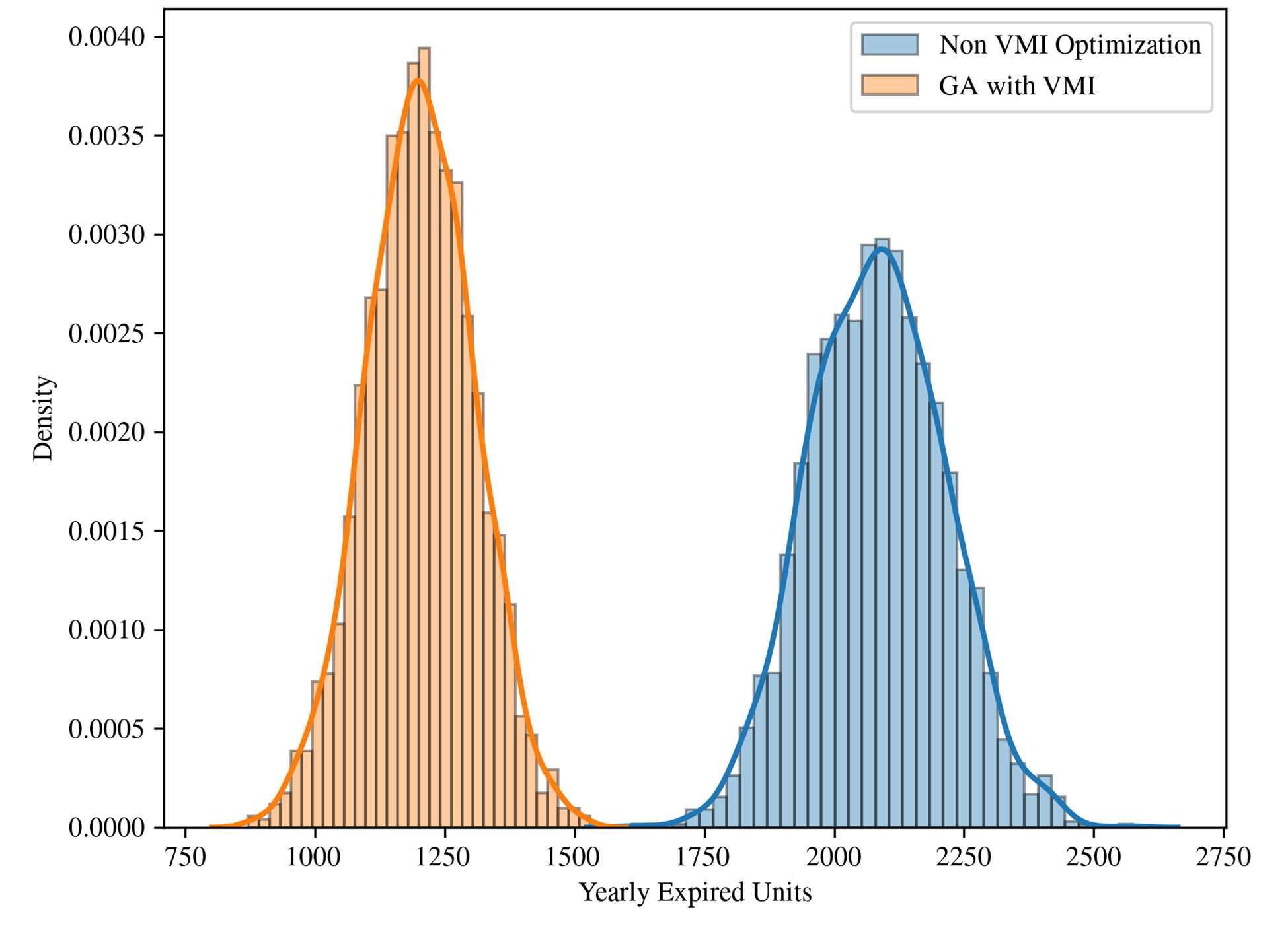 Figure 7.
Expired Units Comparison
Figure 7.
Expired Units Comparison
Own Source
As for the total stock-outs, the results were somewhat counterintuitive. The VMI model averaged 94.91 stock-outs, with a standard deviation of 25.26. At the same time, the non-VMI model averaged 72.98 with a standard deviation of 15.80, so in this case, the non-VMI model was not only better but less variable. Obviously, because this component was the most severely punished in the fitness function, it would be the lowest of all, and it is. It is important to remember that the average expired units in the VMI model was 1202.99, a value more than 12 times the one we observed in the average stock-outs. Still, the stock-outs reported by the non-VMI model were lower, but this is a logical result because the order-up-to values for the hospitals in this model were calculated under the assumption that all orders would be completely fulfilled. Hence, all hospital order-up-to values in the non-VMI model are higher than their VMI equivalents, resulting in higher orders overall, potentially reducing the stock-outs (but performing worse overall).
Nonetheless, the analysis of the resultant service levels shows that this difference is almost irrelevant compared to the total demand. If we calculate this service level for the VMI model, we average 99.32% overall runs, with a standard deviation of 1.77 X 10-3. On the other hand, the non-VMI model scores 99.48% on average overall runs, with a standard deviation of 1.11 X 10-3. The difference between these two means is merely 0.16%. This allows us to conclude that we are reaching nearly identical service levels between both models while significantly reducing the total outdated units and the total cost of operating the system.
Conclusions
The blood supply chain continues to be a very active topic. In particular, platelet inventory has received substantial attention in recent years. However, most publications explore non-collaborative strategies. Hence, we showed that collaborative methodologies such as VMI can considerably improve the key performance indicators compared with non-collaborative systems.
A combination of simulation and optimization allows for solving complex problems. On the one hand, the use of simulation allows to include the uncertainty present in the system; on the other hand, the genetic algorithm evolves to optimal or near-optimal policies that implicitly consider that uncertainty. This creates a robust framework to solve problems that could be intractable by analytical methods or single methodologies.
Even if collaborative methodologies (we are considering VMI here) represent additional implementation challenges, they tend to be more scalable than their non-collaborative counterparts. As interacting systems grow, keeping all information centralized and readily available makes much more sense. Also, by introducing a central information element, further integrations become less cumbersome, and the total work needed to keep the system running is minimized. It is also known that data integrity and reliability may be compromised when every entity decides to gather and manage information on its own.
One of the most important aspects of collaborative strategies is that information can be available to the different actors of the system. In the case of a VMI system, the supplier must have access to real-time inventory levels at each demand point. Otherwise, quality replenishment decisions are going to be challenging to take.
The present paper studied a VMI strategy for the blood supply chain. However, other aspects such as different types of demand (for young and old platelets) and transshipment between hospitals should be studied for some systems. In addition, recent techniques such as reinforcement learning have also shown promising results for complex inventory systems. In terms of collection, the study of donors’ behavior and donor scheduling could help to reduce the variability in donations. Finally, recent situations such as the COVID 19 pandemic have had a high impact on the blood supply chain; while the lockdowns and other policies reduce donations, demand for some products can be increased due to new treatments such as plasma transfusions.
References
[1] J. Beliën and H. Forcé, “Supply chain management of blood products: A literature review,” Eur. J. Oper. Res., vol. 217, no. 1, pp. 1–16, 2012, . https://doi.org/10.1016/j.ejor.2011.05.026
[2] A. F. Osorio, S. C. Brailsford, and H. K. Smith, “A structured review of quantitative models in the blood supply chain: a taxonomic framework for decision-making,” International Journal of Production Research. Taylor & Francis, pp. 1–22, 2015, . https://doi.org/10.1080/00207543.2015.1005766
[3] A. Pirabán, W. J. Guerrero, and N. Labadie, “Survey on blood supply chain management: Models and methods,” Comput. Oper. Res., vol. 112, p. 104756, 2019, https://doi.org/10.1016/j.cor.2019.07.014
[4] G. Figueira and B. Almada-Lobo, “Hybrid simulation–optimization methods: A taxonomy and discussion,” Simul. Model. Pract. Theory, vol. 46, pp. 118–134, Aug. 2014, https://dx.doi.org/10.1016/j.simpat.2014.03.007
[5] A.-T. Nguyen, S. Reiter, and P. Rigo, “A review on simulation-based optimization methods applied to building performance analysis,” Appl. Energy, vol. 113, pp. 1043–1058, 2014, https://doi.org/10.1016/j.apenergy.2013.08.061
[6] M. Gansterer, C. Almeder, and R. F. Hartl, “Simulation-based optimization methods for setting production planning parameters,” Int. J. Prod. Econ., vol. 151, pp. 206–213, 2014, https://doi.org/10.1016/j.ijpe.2013.10.016
[7] T. Roh, T. Lal, and T. Huschka, “Simulation based optimization: Applications in healthcare,” 2015, 10.1109/WSC.2015.7408251
[8] R. Haijema, J. van der Wal, and N. M. van Dijk, “Blood platelet production: Optimization by dynamic programming and simulation,” Comput. Oper. Res., vol. 34, no. 3, pp. 760–779, 2007, [Online]. Available: http://www.sciencedirect.com/science/article/pii/S030505480500119X .
[9] R. Haijema, N. van Dijk, J. van der Wal, and C. Smit Sibinga, “Blood platelet production with breaks: Optimization by SDP and simulation,” Int. J. Prod. Econ., vol. 121, no. 2, pp. 464–473, 2009, https://doi.org/10.1016/j.ijpe.2006.11.026
[10] N. van Dijk, R. Haijema, J. van der Wal, and C. S. Sibinga, “Blood platelet production: a novel approach for practical optimization,” Transfusion, vol. 49, no. 3, pp. 411–420, 2009, https://doi.org/10.1111/j.1537-2995.2008.01996.x
[11] J. T. Blake, N. Heddle, M. Hardy, and R. Barty, “Simplified platelet ordering using shortage and outdate targets,” Int. J. Heal. Manag. Inf., vol. 1, no. 2, pp. 145–166, 2010.
[12] D. Zhou, L. C. Leung, and W. P. Pierskalla, “Inventory management of platelets in hospitals: Optimal inventory policy for perishable products with regular and optional expedited replenishments,” Manuf. Serv. Oper. Manag., vol. 13, no. 4, pp. 420–438, 2011, https://doi.org/10.1287/msom.1110.0334
[13] U. Abdulwahab and M. I. M. Wahab, “Approximate dynamic programming modeling for a typical blood platelet bank,” Comput. Ind. Eng., vol. 78, pp. 259–270, 2014, https://doi.org/10.1016/j.cie.2014.07.017
[14] D. Dalalah, O. Bataineh, and K. A. Alkhaledi, “Platelets inventory management: A rolling horizon Sim–Opt approach for an age-differentiated demand,” J. Simul., vol. 13, no. 3, pp. 209–225, 2019, https://doi.org/10.1080/17477778.2018.1497461
[15] I. Civelek, I. Karaesmen, and A. Scheller-Wolf, “Blood platelet inventory management with protection levels,” Eur. J. Oper. Res., vol. 243, no. 3, pp. 826–838, 2015, https://doi.org/10.1016/j.ejor.2015.01.023
[16] R. Haijema, N. M. van Dijk, and J. van der Wal, “Blood Platelet Inventory Management,” in Markov Decision Processes in Practice, R. J. Boucherie and N. M. van Dijk, Eds. Cham: Springer International Publishing, 2017, pp. 293–317. https://doi.org/10.1007/978-3-319-47766-4_10
[17] H. Jalali and I. Van Nieuwenhuyse, “Simulation optimization in inventory replenishment: a classification,” IIE Trans., vol. 47, no. 11, pp. 1217–1235, 2015, 10.1080/0740817X.2015.1019162
[18] C. S. Pramudyo, “Genetic Algorithm Parameters in a Vendor Managed Inventory Model,” IJID (International J. Informatics Dev., vol. 7, no. 1, p. 36, Jan. 2019, doi: 10.14421/ijid.2018.07108.
[19] A. Beklari, M. S. Nikabadi, H. Farsijani, and A. Mohtashami, “A Hybrid Algorithm for Solving Vendors Managed Inventory (VMI) Model with the Goal of Maximizing Inventory Turnover in Producer Warehouse,” Ind. Eng. Manag. Syst., vol. 17, no. 3, pp. 570–587, 2018, [Online]. Available: https://iemsjl.org/journalarticle.php?code=63301
[20] G. Subramaniam and A. Gosavi, “Simulation-based optimisation for material dispatching in Vendor-Managed Inventory systems,” Int. J. Simul. Process Model., vol. 3, no. 4, p. 238, 2007, https://doi.org/10.1504/IJSPM.2007.016314
[21] W. Liu, G. Y. Ke, J. Chen, and L. Zhang, “Scheduling the distribution of blood products: A vendor-managed inventory routing approach,” Transp. Res. Part E Logist. Transp. Rev., vol. 140, p. 101964, Aug. 2020, https://doi.org/10.1016/j.tre.2020.101964
[22] T. A. Al-Ameri, N. Shah, and L. G. Papageorgiou, “Optimization of vendor-managed inventory systems in a rolling horizon framework,” Comput. Ind. Eng., vol. 54, no. 4, pp. 1019–1047, May 2008, https://doi.org/10.1016/j.cie.2007.12.003
[23] F.-M. De Rainville, F.-A. Fortin, M. Gardner, M. Parizeau, and C. Gagné, “DEAP: A Python framework for Evolutionary Algorithms,” in GECCO’12 - Proceedings of the 14th International Conference on Genetic and Evolutionary Computation Companion, 2012, pp. 85–92, https://doi.org/10.1145/2330784.2330799
[24] F.-A. Fortin, F.-M. De Rainville, M.-A. Gardner, M. Parizeau, and C. Gagné, “Evolutionary Tools — DEAP 1.3.1 documentation.” 2020, Accessed: Jul. 29, 2020. [Online]. Available: https://deap.readthedocs.io/en/master/api/tools.html
[25] A. F. Osorio, S. C. Brailsford, H. K. Smith, S. P. Forero-Matiz, and B. A. Camacho-Rodríguez, “Simulation-optimization model for production planning in the blood supply chain,” Health Care Manag. Sci., vol. 20, no. 4, pp. 548–564, 2017, https://doi.org/10.1007/s10729-016-9370-6
Notes
*
Research paper. Article of scientific and tecnological investigation
Author notes
a Corresponding author. E-mail: afosorio@icesi.edu.co
Additional information
How to cite this article: J.D. Carvajal-Hernández, A. F. Osorio-Muriel, “A Simulation-Based Optimization Algorithm for the Vendor-Managed Inventory Problem for Blood Platelets” Ing. Univ. vol. 26, 2022. https://doi.org/10.11144/Javeriana.iued26.sboa






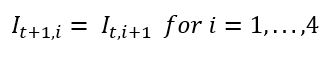 (1)
(1)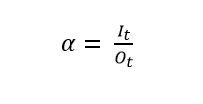 (2)
(2)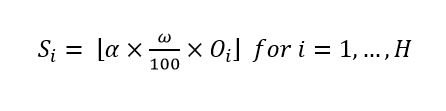 (3)
(3)
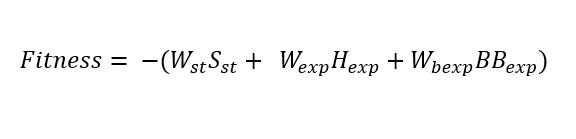 (4)
(4)









