Introduction
Wireless communications technologies have grown significantly in the last decade. The services offered go from short messages service (SMS) to real-time voice communications and, recently, very high data rate transfer with the fourth generation (4G) of mobile networks. Lately, software-defined radio (SDR) and cognitive radio (CR) concepts have shown huge potential and have been called to be an entirely new generation of configurable wireless communications systems. With this remarkable development in wireless communication technologies, many efforts have been put over the table to develop new ways of assisted learning in electromagnetic transmission theory. For students to design and operate wireless communication systems and other applied electromagnetics solutions, they must understand deeply all the basic concepts and laws on how electromagnetic waves propagate in different media; that is, understand the fundamental phenomena related to wireless communication channels. The work by Maxwell in 1855 titled On Faraday’s lines of force [1]presented a simplified model of Faraday’s work and how electricity and magnetism are related, passing later through Maxwell’s discovery that electromagnetic fields propagated to the speed of light in 1861. Both have been breaking moments in human history that every electronic or related engineering student should be known. However, there is a vast misunderstanding about Maxwell’s work and how his contributions are part of our daily lives. The lack of context and clear relationships linking Maxwell’s laws interpretation and the present wireless technologies have undermined the electromagnetic theory.
The electromagnetic-based undergraduate courses are taught in many computer sciences, including electric and electronic engineering programs worldwide. In the following, some of the courses from the top 10 best engineering universities globally are reviewed [2]. The MIT’s electromagnetic course [3] is presented as an introductory course, emphasizing fundamental concepts and applications of Maxwell’s equations by covering topics such as polarization, wireless communications, forces and energy, phase matching, dielectric waveguides, optical fibers, transmission line theory and circuit concepts, dipole antennas and equivalent principle for radiation. The course features a series of MATLAB and physical demonstrations which help to illustrate electromagnetic principles such as electrodynamics and wave propagation, guidance, and radiation of electromagnetic waves. Other courses from the University of Michigan [4] and the Arizona State University proposes a similarly applied electromagnetics syllabus covering additional novelty electromagnetic applications topics like millimeter-wave antenna measurements, microwave fabrications and characterization devices, MEMS circuits, Computational Electromagnetics (CEM), active and passive remote sensing, plasma electrodynamics, and EM materials. The description of both courses emphasizes the essential role of the applied electromagnetics area in a variety of modern applications ranging from wireless technologies, environmental concerns, life sciences, and transportation. On the other hand, a more traditional electromagnetic course syllabus is given at Stanford [5], Berkeley [6], and Caltech University [7], which covers the basic principles of Maxwell’s equations in electrostatic and electrodynamic regimes to more complex on theoretical topics of radiation and propagation.
Many authors have addressed that most undergraduate students often perceive learning electromagnetic theory and related topics as highly complicated and problematic [8], [9]. For instance, the work in [10] proposes an electromagnetics course as an appetizer for computer science (CS) and information technology (IT) undergraduates, particularly since most of those students will not pursue a career specializing in electromagnetics. Other works, like the one in [11]describes and discusses the application of two different approaches for teaching an undergraduate electrical engineering applied electromagnetics course, which includes the study of electromagnetic theory combined with two practical applications: i) radio frequency engineering and ii) radar and antenna design, both of them through laboratory experiments, design experiences, and projects. Other works [12] addressed the electrical engineers’ perception of their education in the introductory electromagnetic field theory courses and their applicability in working life.
The intrinsic difficulty of electromagnetic-based courses is probably because it requires a combination of a deep understanding of mathematical and physical concepts for their completion [8]; this fact, combined with the misconception that electromagnetism has little relevance in our daily life’s technological applications, have motivated universities worldwide to eliminate or reduce courses in the foundations of electromagnetics or teach incomplete and sparse courses of electromagnetic theory not reach solid well-grounded learning. A brief review of professors’ websites who teach electromagnetic theory courses shows a frequency reduction of the lectures in the last decade [13], [14], [15]. Despite this current trend, to name one of the multiple electromagnetic applications, most current IC technologies perform wireless communication access to the radio frequency medium. Hence, knowledge of electromagnetic phenomena and modeling techniques is still important to design and manage such technologies. Even more, the industry demands engineers who have compelling insights and can create and develop novel solutions to the rapidly changing wireless technology [9].
Nonetheless, electromagnetism courses are typically taught using lectures on Maxwell’s equations either in differential or integral forms [16], [17]. These instructional strategies require that professors capture students’ attention and become the source of knowledge. Also, these strategies often lack practical insights, hands-on activities, and context on daily life technologies [18], [19], which reinforces the notion that electromagnetism courses are tedious or old-fashioned instead of promoting that these are engineering courses that should motivate students.
We argue that teaching electromagnetism courses with traditional strategies leads students to fail the course and demotivates students to follow the area of wireless communications throughout their engineering careers. Hence new ways of teaching these courses have gained attention. One necessary approach is Visual Electromagnetics (VEM). VEM is an interactive and visual learning environment to provide a more appealing and intuitive means of studying electromagnetics [20]. Three-dimensional (3D) models have been proved helpful for students with high spatial ability in their learning process [21]. Because of the continuous growth of computational power, other numerical approaches have also been proposed [22], which in consequence, have led to novel ways of teaching by employing computational electromagnetics (CEM) [23]. For example, Computer-Aided Instruction (CAI) approaches have used multimedia and software simulation tools very effectively in the last 20 years [24]. More recent works have proposed Method of Moments (MoM) simulation platform for scattering problems under a MATLAB environment [25], computer-assisted problem-based learning projects employing the Finite Difference Time Domain method (FDTD) to model transmission lines performance [26], or have combined theoretical concepts in textbooks and experimental platforms with multimedia interactive interfaces [27].
In general, as a valid response to traditional instruction, project-based learning (PBL) has been proposed as an instructional strategy that increases the attractiveness of the curriculum and students’ interest [28]. In electronics, PBL is associated with an improvement in the overall average grade of the courses [29]. PBL has oriented in that students face a specific problem in a current context where theoretical concepts are directly experienced during the development process [30], [18]. Recent works have been focused on estimating the success of PBL by using ubiquitous sensors [31]. In this sense, the Electronics Engineering program of our University is immersed in a curricular change process based on the conceiving, designing, implementing, and operating (CDIO) initiative. This curriculum change aims to improve the program with a comprehensive education that considers the local and global context, emphasizing the process of conceiving-designing-implementing-operating products, processes, and systems [32]. A key feature of CDIO programs is the integration of learning experiences that lead to the acquisition of disciplinary knowledge and skills [33], mainly using PBL and active learning instructional strategies [34], which involve students as active participants in their learning process [35], help them to make better connections among concepts, and facilitate the application of this knowledge to complex, contextualized, and real problems [32].
This paper describes and discusses the implementation of a project-based undergraduate course on applied electromagnetics in the electronics engineering program into the new CDIO curriculum where students are involved as active participants in their own learning experience through PBL. Projects are designed to enhance the practical learning of three core concepts of the course.
In summary, the contributions of this paper are as follows:
-
The outline of a project-based applied electromagnetics course program based on the CDIO philosophy.
-
The proposed projects presented, giving the related core concepts, motivation, context, results, the required disciplinary knowledge, and CDIO skills.
-
The validation and analysis of the student’s learning effectiveness by following this methodology, addressing the student’s final grades improvement and perception of difficulty.
-
The following sections are organized: Section 2 gives an in-depth description of the proposed course, including its learning objectives. Section 3 introduces the CDIO working methodology explaining how each project aligns with the CDIO initiative. Section 4 presents the PBL projects, including insights into their context, motivation, and challenges. Section 5 presents the project results. Section 6 shows the analysis and discussion of the evaluation of the instructional strategy. Finally, Section 7 concludes the paper with remarks and future perspectives.
Course Proposal
The 48-h one-module undergraduate course called Electromagnetic Transmission was designed to help students learn the fundamentals of electromagnetics through understanding the generation and propagation mechanism of electromagnetic waves from both the classical Maxwell’s equation perspective and the electronic engineering application field. The idea is to empower the students to understand the modern impact of wireless technologies in our current society; hence, the course provides basic knowledge of radio frequency (RF) systems and antenna radiation elements and design used in current telecommunications systems. Even though the course is project-based, it includes theoretical lessons guided towards developing the projects to enforce core concepts based on simulation and graphical tools. For every hour of the lecture, students are encouraged to invest 2 h for independent work. The total student workload for the course is 140-150 h. Students regularly take the course in the third year in the curriculum after approved five mathematics courses covering differential equations, complex variables, single and multivariable calculus, and four physics courses covering mechanical, electrical, electrostatics, and magnetostatics physics.
The course is divided into four modules as follows:
-
Dynamics of Electromagnetic fields.
-
Electromagnetic wave’s propagation in the absence of sources.
-
Electromagnetic wave’s radiation in the presence of sources.
-
Introduction to Computational Electromagnetics (CEM).
The module Dynamics of Electromagnetic field addresses the main electromagnetics concepts and phenomena using the perspective of Maxwell’s equations. It starts from the static case and goes through the dynamic case. The main goal of this module is to provide students with the tools to describe, mathematically and physically, the dynamic behavior of the electromagnetic field. The theoretical foundation of Maxwell’s equations allows students to have an in-depth insight into electromagnetic phenomena in any engineering application.
Electromagnetic wave propagation in the absence of sources begins by addressing the mathematical foundation of electromagnetic wave propagation in the absence of sources by introducing the Helmholtz equation in isotropic, homogeneous, and linear media. A description of a plane wave is then given due to its relevance for modeling and understanding the basics of wireless transmission systems. Essential concepts of electromagnetic waves are overviewed, such as polarization, complex power density, and Poynting vector. All the wave phenomena are reviewed by considering reflection, refraction, and diffraction models. The module focuses on real case scenarios such as propagation of Wi-Fi signal in indoor scenarios and RF atmosphere propagation for radio link design.
Electromagnetic waves radiation in the presence of sources is dedicated to answering how antennas generate electromagnetic waves. In this part, we introduce, to the surprise of most of the students, how a simple monopole antenna radiates a vertical polarized electromagnetic plane wave just by feeding the antenna by an RF signal source generator. This module covers the vector and scalar potentials formulations for obtaining electromagnetic fields in the Fraunhofer region and antennas radiation patterns.
With this approach, students can easily go through the antenna concept and its fundamental parameters. The module Introduction to Computational Electromagnetics (CEM) introduces a general perspective of the algorithms and methods to obtain a full-wave solution to different electromagnetic problems. Two main methods are reviewed in detail for 1D and 2D, the Method of Moments (MoM) and the Finite Difference Time Domain (FDTD) method. These two methods cover two kinds of full-wave solutions in the frequency and time domain, and it allows students to learn two general approaches to computationally solving Maxwell’s equations. Notably, this module is intended to understand the fundamentals of the computational methods that students employed in a specific problem for the Colombian context, such as the landmine detection described later in Section IV.
The course mainly consists of theoretical and project-based lessons. Many course concepts are supported by simulation tools either during the lecture or the project development. Course notes, project proposals, and course schedules are given to the students at the beginning of the course. In this way, students can organize their agendas all semester long. The textbooks suggested [36], [37], [38], [39], [40], [41], [42], [43], [44] are available at the university library or online [45] which are thought to support the student’s learning process. Table 1 gives the course outline, the number of hours per lecture, and the textbook references. The relationship of the course’s modules with the projects is explicitly presented in each project’s description section.
Table 1.
Syllabus of the Project-Based Electromagnetic transmission course

Own source
It is worth noticing that the modules do not intend to be highly specialized in the covered topics. In fact, because of the CDIO vision, the fundamental goal of the course is to integrate rich learning experiences leading to the acquisition of enduring understandings (i.e., core concepts) and the skills in the gradualness proposed for the course. The project-based approach is an active learning tool where students are highly involved in their own learning process. The course takes relevance to the program curriculum since the course has a strong relationship with the physics courses taught in the first and second years and the application courses taught in the 4th and 5th years.
Main concepts, learning difficulties, and misconceptions
This course focuses on three main concepts selected according to the most common learning difficulties derived from misconceptions that students usually have. The first learning difficulty, related to Electrodynamics from Maxwell’s equations perspective, derives from two misconceptions. The first misconception is that Maxwell’s equations are only just equations, which are historically taught by presenting the equations as a general list of rules that must be checked for any field expression without deeper insights. From this point, students can only learn about mathematical vector operators applied to one physical phenomenon but not further details about how energy propagates through a dynamic electromagnetic field. The second misconception derives from the fact that students believe that the electric and magnetic fields are static, even when time dependence is included. This is a hard paradigm to teach since, although students have learned in previous courses principles about electrostatics, magnetostatics, and waves in physical media such as sound or water waves, they still have a hard time understanding electromagnetics.
The second learning difficulty is related to ii) the Dielectric properties of materials since, at this point of the study plan, students have a Newtonian understanding of the physical world. This fact derives from the misconception that materials only can be described from their mass density, and this property only can be altered by forces. Therefore, introducing new properties like permittivity, permeability, and conductivity is problematic.
The third learning difficulty is more a perspective of the usefulness of the course itself, derived from the misconception that electromagnetics has no application in real life. In addition, computational electromagnetics has been particularly new from the educational perspective since the proliferation of computers in the last 20 years. This fact leads to electromagnetics courses rarely covering fundamental concepts in this area, making itself an open issue in education.
The proposed projects are designed to solve the learning difficulties and are meant to be developed in groups of 3 students with a developing time of 20 h of independent work. The projects are assigned in three terms during the semester, according to the topics covered in the course.
Students continuously received feedback from the professor and the course’s teaching assistant. The final evaluation of each project is done through a technical report framed in the CDIO framework description.
CDIO framework
The methodology of the course is based on the CDIO framework, involving active learning through PBL. CDIO is based on constructive alignment, which is a model that involves the permanent interaction between teaching and learning activities, intended learning outcomes, and assessment [32].
With the CDIO framework, students develop their projects so that while acquiring knowledge and putting them into practice, they improve their group work skills, develop their critical thinking, and strengthen their written and oral communicative skills [32], [46]. CDIO framework consists of four stages used to develop the proposed projects in this course.
Conception stage
The purpose of this stage is the conceptualization of the project. Once the concepts and theory have been taught in class, students appropriate these concepts and apply them to the project. In the conception stage, the teacher shows the relationship between the project, the related concepts, and the expected learning outcome in the project’s development. By engaging students in thinking about concepts and new knowledge and requiring an overt response, students improve their learning process and their deep understanding of what and how they learn [32]. Likewise, the components of each project are clearly defined and are presented at each phase of the project and the end of it. This stage allows the students to understand the generality of the project and the specific points that must be developed. Requirements of this stage are mainly related to the topics that have to be already covered for each project. Constraints are related to the maximum number of students per group and the submission time of the project’s reports.
Design stage
The purpose of this stage is the design of the project. In working groups and with the teacher’s guidance, students must define the components and tools involved, develop the plans and algorithms for the project, and design the project outcome. This stage can be done in different ways depending on the project to be developed. For example, in the first projects, students are suggested to use a specific software as a simulation tool; however, no restrictions are imposed other than those given at the conception stage.
Implementation stage
In this stage, the students materialize the proposed design (hardware, software, testing), validate the accomplishment of the given restrictions, and evaluate the degree of compliance with the requirements indicated in the conception and design stages.
Operation stage
This stage involves demonstrations of the prototype (software or hardware). It allows students to understand their prototype working in the real world. Additionally, they can obtain feedback from users (other students) and an expert (teachers). As part of the final evaluation, they must present a written technical report in IEEE format. After completing all the steps, students receive feedback from the teacher. If necessary, they must correct parts or components of the project delivered. Once this stage is completed, the students obtain their respective grades. Additionally, students must complete a survey at the end of the course, in which they must evaluate the course, its instructional strategy, and the proposed projects.
Projects’ description
Project I: Vector Analysis of electromagnetic fields
This project’s motivation is directly related to the abstraction of how a dynamic electromagnetic field propagates energy in a dielectric media as a wave. The project topic is related to modules 1.1, 1.2, 2.1, 2.2, 3.1, 3.2, and 3.3 of the courses (Table 1). The main goal addresses the student’s difficulty understanding Faraday’s and Maxwell’s premise that an electromagnetic field works as a media for energy propagation. A visualization model helps students find similarities with energy propagation in physical media such as the water or sound waves. Besides, some important concepts are addressed, e.g., the difference between vector field component and propagation direction, polarization of an electromagnetic wave, standing waves, radial waves, power radiation, and antenna array.
The students are asked to use Matlab as a visualization tool with an initial question on how an electromagnetic vector field can visually be represented with a proposed SteadyState Electric field expression. Students must obtain the magnetic field component with the proposed expression by using Maxwell’s equations. Having both field expressions, they are asked to include time dependence and propose a visualization method to show and explain the energy propagation phenomena intuitively. With the initial electromagnetic wave representation set up, several possibilities are open to activate their learning about important electromagnetic wave concepts. One of them is how a planar front wave should look or what would happen when another wave of the same intensity propagates in a completely opposite direction, interfering with the actual wave. This strategy teaches the concept of reflecting and standing waves. Additional concepts are also approached, as is the case of wave polarization, by asking them what would happen if the Electric field had more than one transverse component? And how the wave propagates when the amplitude and phase difference is changed.
Then, students are asked to set up an additional propagating wave changing from cartesian to the cylindrical or spherical coordinate system. This new configuration helps them visualize radial front waves and allows them to explore concepts such as antenna radiation by proposing a scenario where the center of the radial wave is a radiating structure and what would happen when the radiating is, for example, changed by focusing more intensity in one particular region than others. From this point, the antenna array concept is easily introduced by asking them to configure two radiating elements with different amplitude, phases, and spacing between them.
The students can choose a visualization method, the frequency wave, and the media where it is propagating. Additionally, in the CDIO framework, only an initial conception and description are given to students. They must perform modeling and Design based on the theory seen in class and software implementation to visualize of the electromagnetic wave, thus fulfilling the given requirements and answering all the formulating questions.
Project II: Dielectric-properties measurement system
This project aims to show the importance of knowing the dielectric properties of materials where electromagnetic waves propagate. In the given context, students must acquire in-depth insights into the meaning of materials’ permittivity, permeability, and conductivity, besides how these concepts can be applied in radio waves propagation and materials characterization for diverse purposes. The project topic is related to modules 1.2, 2.1, and 2.2 (Table 1). Additionally, during the project development, students face challenging issues, e.g., finding, designing, and implementing a reliable measurement method supported by simulation through Ansoft Electromagnetics. As a result, the project addresses the following concepts: Boundary conditions and electromagnetic surface-wave propagation, electric and Magnetic field coupling, electromagnetic wave propagation in guided media, phase and group wave velocity, wave dispersion, reflection coefficient, and electromagnetic wave resonance, among others. In this project, the students must:
-
Designing, modeling, simulating, and implementing the selected method, including the excitation coupling.
-
Measuring the implemented method to validate the theoretical and simulated results.
-
Once validated, obtaining the dielectric properties of a liquid, solid or semi-solid load using the implemented method.
-
Comparing the obtained dielectric properties of the load with a valid dataset.
The students can choose the measurement method and the working frequency upon well-grounded criteria. In this project, the students receive the Conception, and they must perform modeling and Design based on the theory seen in class. Later, using Ansoft Electromagnetics, they implement the measurement methods and observations necessary to obtain the characteristics of the dielectric material. The operative part is limited to comparing and validating the results on the dielectric properties with a set of loaded data.
Project III: Impulse-based Ground Penetrating Radar (GPR) simulation for landmine detection
The main motivation of the project is to show students how the main concepts taught during the course can be applied in a real scenario. The project topic involves concepts in modules 2.3, 2.4, 3.1, 4.1, 4.2, and 4.3 of the course (Table 1). The problem exposed in the project directly impacts the national context since Colombia is one of the most mine-affected countries globally, with 10751 registered victims since 1990. Although the internal conflict in Colombia is coming to an end, there still are regions in the country with over 10000 potentially hazardous areas that require urgent mine clearance, according to recent Colombian government statistics. Therefore, students indeed found the project very interesting from the applicative point of view, particularly if they could identify an actual application in the Colombian context, which has turned out to be a key point in its learning process.
Students address important course concepts during the project development, such as wave propagation in different media, reflection, refraction of electromagnetic waves, wave velocity and time of arrival, electromagnetic computational time-domain methods, space domain discretization, and microwave imaging concepts. With the aforementioned context, the students are asked to implement and simulate a 1D FDTD method by setting up the distance of the space domain, the grid points, the grid parameter, the excitation signal, and the boundary condition. In this fashion, they need to adapt the simulation set up with different landmine scenarios considering the air-soil discontinuity and the presence or absence of the explosive artifact. Students can choose the programming language for implementing the FDTD method, the visualization method, and the soil media. Finally, in this project, students can develop a solution to a problem in their environment. They not only apply the concepts seen in class but also manage to connect these concepts with practical applications, which can have a high impact on people. The two main components in this project are conception and design. No implementation or operation is carried out.
Project results
This section will show firstly the main results of the Projects proposed in section IV. Since most of them include conceiving, designing, and implementing challenges of the CDIO methodology, the results are presented in that manner.
Project I
The students propose a steady-state Electric field expression that must satisfy Maxwell’s equations, such as the one given by equation (1).
There are several approaches for visualizing vector fields in MATLAB. However, the most employed one is using the quiver and quiver3 functions. The magnetic field can be easily computed by applying Maxwell Faraday’s law by using the curl function in MATLAB. Most students choose air as the dielectric media for propagation and plot the field in one single plane for visualization purposes. The resulting plot for the electromagnetic field and the wave-front is shown in Figure 1.
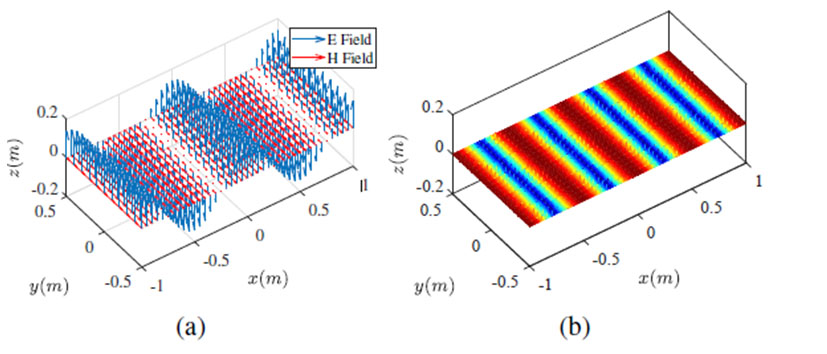 Figure 1
Electromagnetic plane wavefront: a) vector form and b) magnitude form.
Figure 1
Electromagnetic plane wavefront: a) vector form and b) magnitude form.
Own source
With this approach, students can visualize the orthogonal component’s behavior of an electromagnetic field and the wavefront of a planar wave. With the inclusion of time dependence, students can directly understand how a wave solution of form satisfies Maxwell’s equations, being the position and the wave velocity equal to the speed of light. As a result, they can visualize how an electromagnetic field works as an energy propagation medium. The most common approximation followed by the students is using the function movie for sampling the electromagnetic field at different moments in time, as shown in Figure 2.
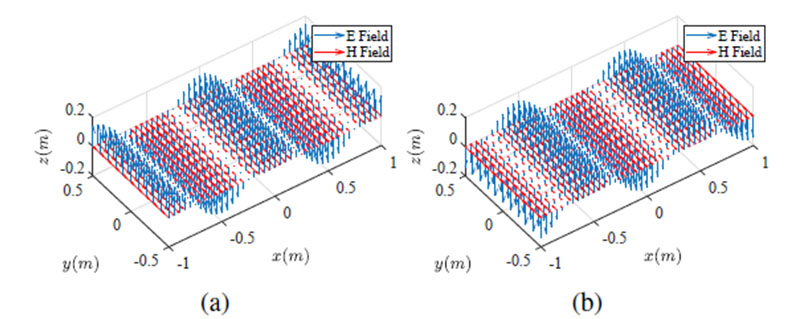 Figure 2
Electromagnetic wave propagation in free space at different times at the z = 0 plane, with a working frequency of 300 MHz at different time moments: a) 0 ns and b) 1.5 ns.
Figure 2
Electromagnetic wave propagation in free space at different times at the z = 0 plane, with a working frequency of 300 MHz at different time moments: a) 0 ns and b) 1.5 ns.
Own source
To show a reflecting and standing wave, students add to the expression in (1), the reflection component as is written in equation (2), and therefore visualize and analyze the resulting wave. Hence, constructive and destructive interference can be easily shown.
When students add to the electric field an additional component, different wave polarization can be visualized. For example, a circular polarized electromagnetic wave is easily implemented by setting up a phase difference of 90° between both components, as described in equation (3). The plot of the electromagnetic wave at the intersection of z = 0 and y = 0 planes is shown in Figure 3.
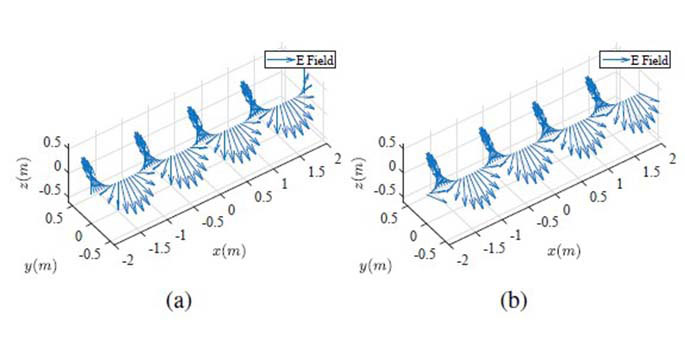 Figure 3 .
Electric component of a right-hand circular polarized electromagnetic wave at different times in the z = 0 and y = 0 plane, with a working of 300 MHz at different time moments: a) 0 ns and b) 1.5 ns.
Figure 3 .
Electric component of a right-hand circular polarized electromagnetic wave at different times in the z = 0 and y = 0 plane, with a working of 300 MHz at different time moments: a) 0 ns and b) 1.5 ns.
Own source
For the radial wavefront, students can use either a cylindrical or spherical coordinate system and propose a new electromagnetic wave solution with radial propagation as the one expressed in equation (4). The proposed radial electromagnetic wave at one moment is shown in Figure 4a. In this manner, students can visualize easily the curl of the magnetic field component of the radial wave and the radial wavefront 4b.
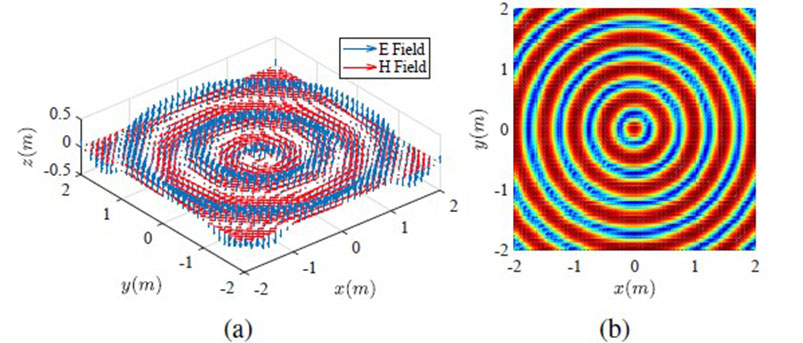 Figure 4 .
Radial electromagnetic wavefront: a) Vector form of an electromagnetic field and b) Magnitude of electric field intensity
Figure 4 .
Radial electromagnetic wavefront: a) Vector form of an electromagnetic field and b) Magnitude of electric field intensity
Own source
They can also compute the Poynting vector to verify the power propagation wave direction.
Students can easily change the electric field expression to focus the radiation in one region with the aforementioned radial wave setup. One possible solution is to include a non-symmetric term into the expression in equation 4 given by a sinusoidal function depending on the azimuth angle φ, as is expressed in equation (5). This solution is very helpful in teaching the radiation pattern of an electric dipole antenna in the E-plane. The proposed electromagnetic wave field is shown in Figure 5a. Students can also obtain the source radiation pattern from the Poynting vector and the electric field magnitude shown in Figure 5b.
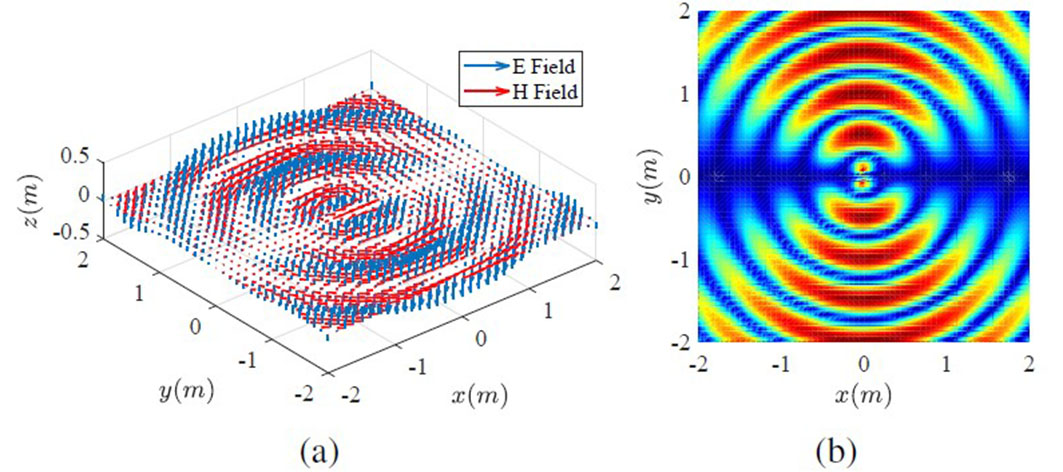 Figure 5 .
Non-symmetric radial electromagnetic wavefront: a) Vector form of an electromagnetic field and b) Magnitude of electric field intensity
Figure 5 .
Non-symmetric radial electromagnetic wavefront: a) Vector form of an electromagnetic field and b) Magnitude of electric field intensity
Own source
Finally, students must include at least two radiation point sources placed along a line spaced with different distances d, for example, varying from λ/8 until (3/2)λ. With this approach, students directly faced the antenna array concept and the constructive and destructive interference of electromagnetic fields produced by two separated radiators with different amplitudes and feeding phases. By doing this, they can already conclude the definition of radiating lobes (Figure 6). Similar approaches for underlying the wave interference principle in antenna array theory are presented in [47].
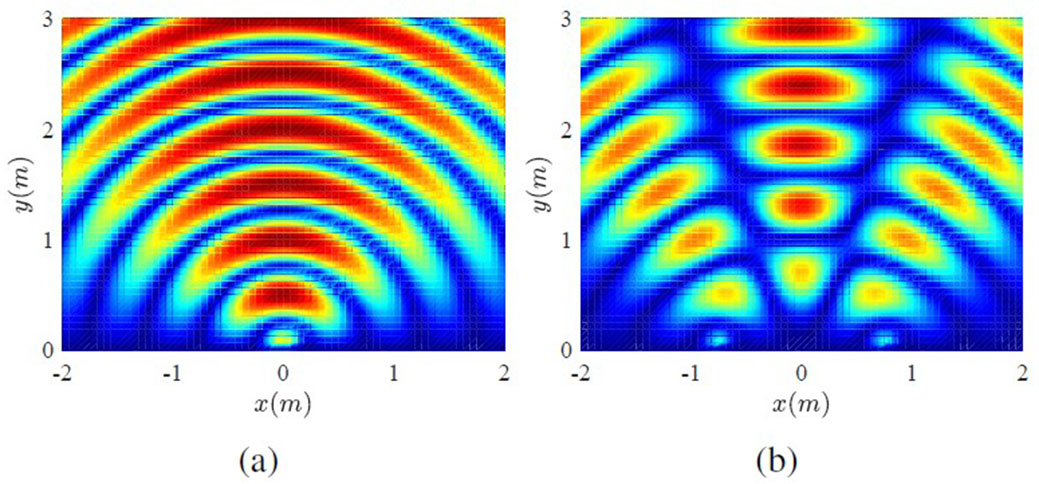 Figure 6 .
Radiation pattern of two radial electromagnetic sources array, separated by: a) λ/8 and b) (3/2) λ distance
Figure 6 .
Radiation pattern of two radial electromagnetic sources array, separated by: a) λ/8 and b) (3/2) λ distance
Own source
Project II
Dielectric measurement based on radio and microwave methods has been extensively studied. The different measurement techniques can be applied in several areas related to electronics, for example, electronic sensor technology design. In this context, students firstly review different measurement methods found in the literature, some works found in the literature related to dielectric measurement techniques over the frequency band of 1 MHz to 1.5 GHz are the ones in [48], [49], [50].
Microwave cavity resonators are other standard techniques employed for high accuracy for permittivity, permeability, and conductivity measurements [51]. Under this method, a perturbation approach is employed, and the mathematical model and principle are introduced in [52], [53]. Several works in literature have addressed this technique with different kinds of cavity resonators for solids and liquids with high accuracy. In particular, the work in [54] and[55]uses a rectangular metallic cavity working in the TE10p mode, while authors in [56] and [57] employed a cylindrical cavity resonator in the TM0n0 mode.
During the conception process in the CDIO framework, students evaluate the requirements of the different techniques by doing a decision matrix where the cylindrical cavity resonator is usually the most implemented and therefore is the one described in this paper. The resonant cavities are commonly analyzed in electromagnetic-based theory courses; their working principles can be found in detail in the course guidebooks[39]. As mentioned before, the most common shapes for resonant cavities are rectangular and cylindrical. In particular, students go for the cylindrical solution since they can use a cookie jar for the implementation by doing a backward engineering process.
A cylindrical cavity is formed by a short-circuited cylindrical waveguide in both of its extremes. The input electric or magnetic field coupling is performed by means of holes in the structure, commonly called irises, or probes by introducing quarter-wavelength monopoles through coaxial connectors, some of these types of cavity excitations are presented in [39].
As in the waveguides, TE and TM modes can propagate in the cylindrical cavities, depending on the working frequency and the type of excitation. The mode determines not only the electromagnetic field components, but also the design parameters, such as the resonance frequency. The most commonly employed mode is the TM010 since it generates a strong electric field around the axis of the cylindrical cavity which makes the structure sensible for permittivity changes of the inner dielectric material.
The resonance frequency of the TM mode, expressed in equation (6), is obtained by computing the solution of the axial component of the electric field from the Helmholtz equation and the boundary conditions.
Where α and h are the radius and the height of the cavity, respectively. χmn is the n-ave zero of the m-order Bessel function, and µ and ε are the permeability and permittivity of the inner dielectric material in the cavity, respectively.
Before the project implementation, students must first understand the electromagnetic field associated with the generated field model. During the implementation, students select the resonance frequency based on the dimensions of the cookie jar. Therefore, they must have the criteria for choosing a proper one according to the desired frequency.
Once the cavity dimensions are defined, students create a simulation model in Ansys Electromagnetics, as shown in Figure 7a and Figure 7b. The simulation results support students in the design process where they can validate the resonance frequency through the reflection coefficient S11 (Figure 8) of the coaxial wave-port and the electric (Figure 7c) and magnetic (Figure 7d) TM010 mode’s field components excited at the inner of the cavity. Students can also simulate both the electric and magnetic excitation probes to select one of them for the implementation.
In the measurement setup, a Rhode&Schwarz ZVA24 Vector Network Analyzer (VNA) was used. Once the measurement is obtained, students analyze the measured and simulated resonance frequency to validate the correct behavior. For the cavity presented in this work, the cavity’s radius and height are α = 8.3 cm and h = 7.9 cm, respectively. By using equation (6), the analytic resonance frequency is fr = 1.383 GHz.
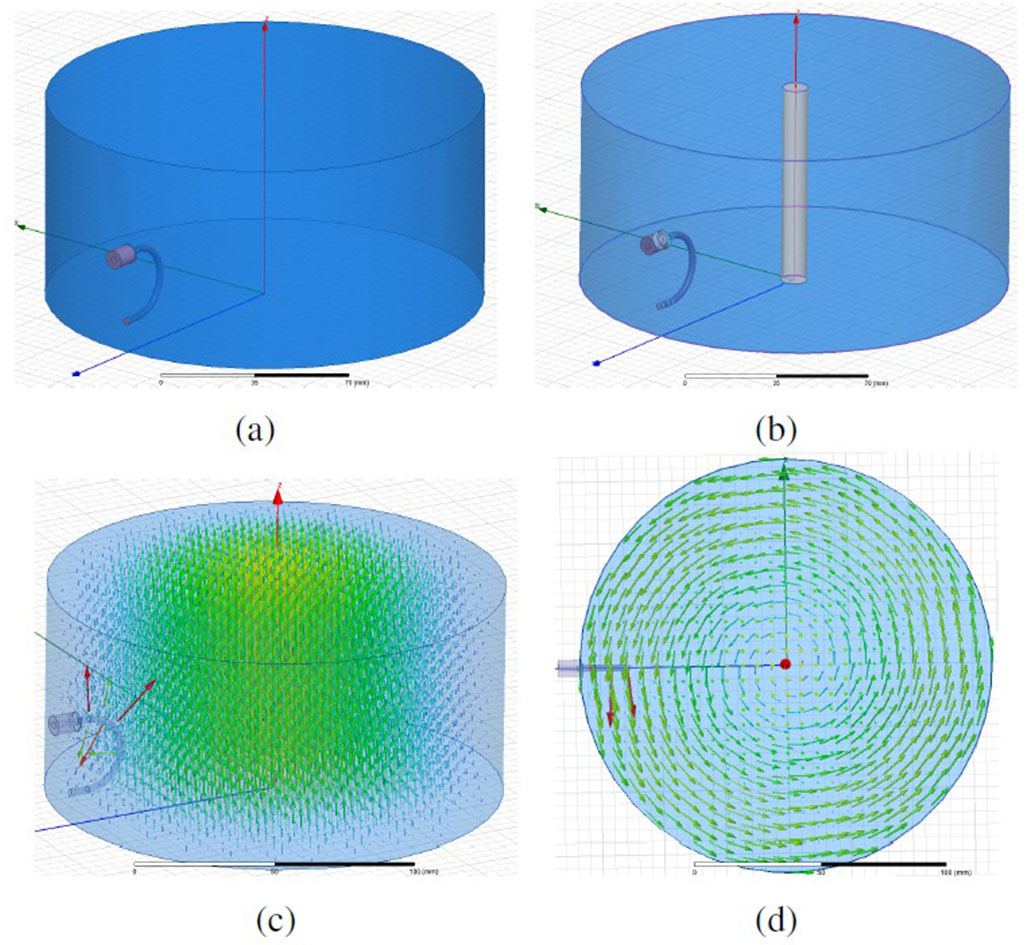 Figure 7 .
Cylindrical cavity for a dielectric measurement perturbation method application: a) Empty simulation model, b) simulation model with silicon sample bar, c) electric field distribution of the TM010 mode, d) magnetic field distribution of the TM010 mode
Figure 7 .
Cylindrical cavity for a dielectric measurement perturbation method application: a) Empty simulation model, b) simulation model with silicon sample bar, c) electric field distribution of the TM010 mode, d) magnetic field distribution of the TM010 mode
Own source
Students use the simulation tool and the lab measurements for the dielectric properties’ estimation. Therefore, during the test, students introduce a dielectric sample bar in the cavity to observe the changing of the resonance frequency of the TE010 mode. With this information, students model the sample bar of an unknown material into the Ansys software, and by changing their dielectric properties, they can reproduce the same frequency shift. This indirect measurement provides an approximate value for the material’s permittivity, permeability, and conductivity. The simulated and measured reflection coefficient S11 is shown in Figure 8.
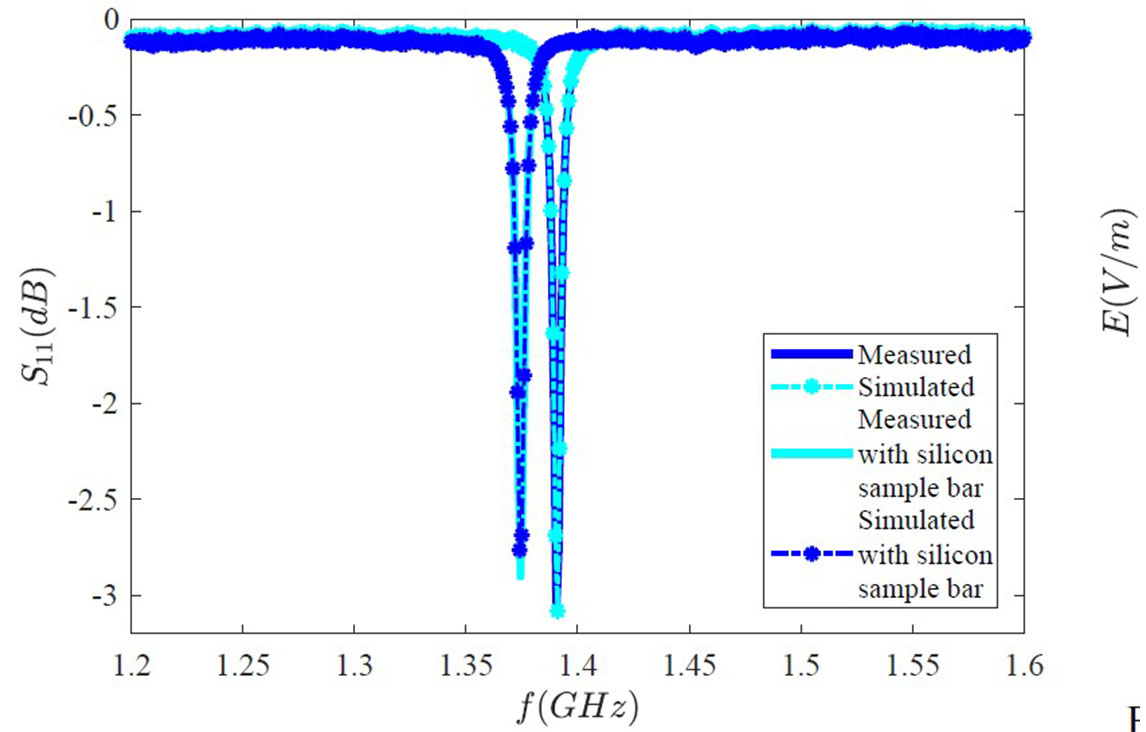 Figure 8 .
Reflection Coefficient (S11) of the cylindrical resonant cavity with and without the silicon sample bar
Figure 8 .
Reflection Coefficient (S11) of the cylindrical resonant cavity with and without the silicon sample bar
Own source
Project III
Within the specified problem context, students must research ground-penetrating radars and their main features, particularly the electromagnetic wave produced by an impulse-based radar transmitter. For the sake of simplicity, they are only asked to simulate a 1-D scenario. For this purpose, they must first obtain the electromagnetic wave equation from Maxwell’s laws in one dimension, considering a one-component planar electromagnetic wave solution like the one expressed in equation (7).
Second, students discretize the space and time domains in and points and, therefore, approximate the partial derivative to its discrete counterpart given equation (8).
By replacing (8) in (7), the FDTD updating equation is obtained in (9), where subscripts and superscripts are used to denote space and time grid points, respectively. Therefore, for simplicity, the electric component of the electromagnetic wave evaluated at a certain point (xn = nΔx) and time (ti = iΔt) into the grid can be rewritten as.
The grid parameter is equal to r = c0Δt/Δx, being c0 the wave velocity in air. With equation (9) and a one-order absorbing boundary condition to simulate an infinite, unbounded computational domain given by equation (10), where represents the index of the boundary point of the discretized space, students can simulate a Gaussian electromagnetic pulse propagating in the air as shown in Figure 9.
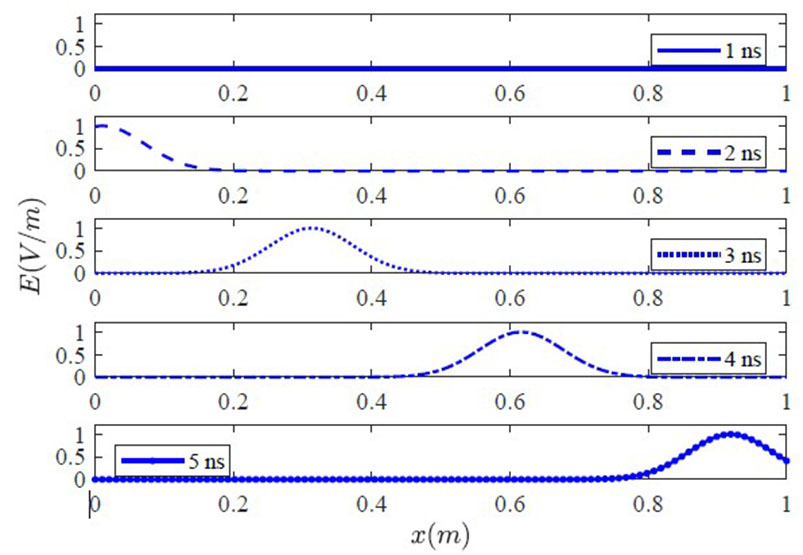 Figure 9 .
Gaussian electromagnetic pulse propagating in air
Figure 9 .
Gaussian electromagnetic pulse propagating in air
Own source
Next, students must modify the grid parameter r in the updating equation in (9) to include an air-soil discontinuity and simulate the reflection scenario of an incident electromagnetic Gaussian pulse where reflection and refraction propagating wave profiles are obtained by registering the wave amplitude at the beginning of the space domain at x0 (Figure 11b). Students also obtained the reflection coefficient and compared it with the one computed analytically given by equation (11), being ηs and ηa are the wave impedance of the electromagnetic field in soil and air, respectively. The propagating wave in an inhomogeneous media with an air-soil discontinuity is shown in Figure 10.
With the time of flight tof = 3.4 ns, considered as the time that the electromagnetic wave takes to arrive since it is transmitted, obtained from Figure 10b, students compute the discontinuity distance d0 from the transmitter by knowing that the wave velocity in air is the one of the light obtaining d0 = c0tof/2 = 0.5 m.
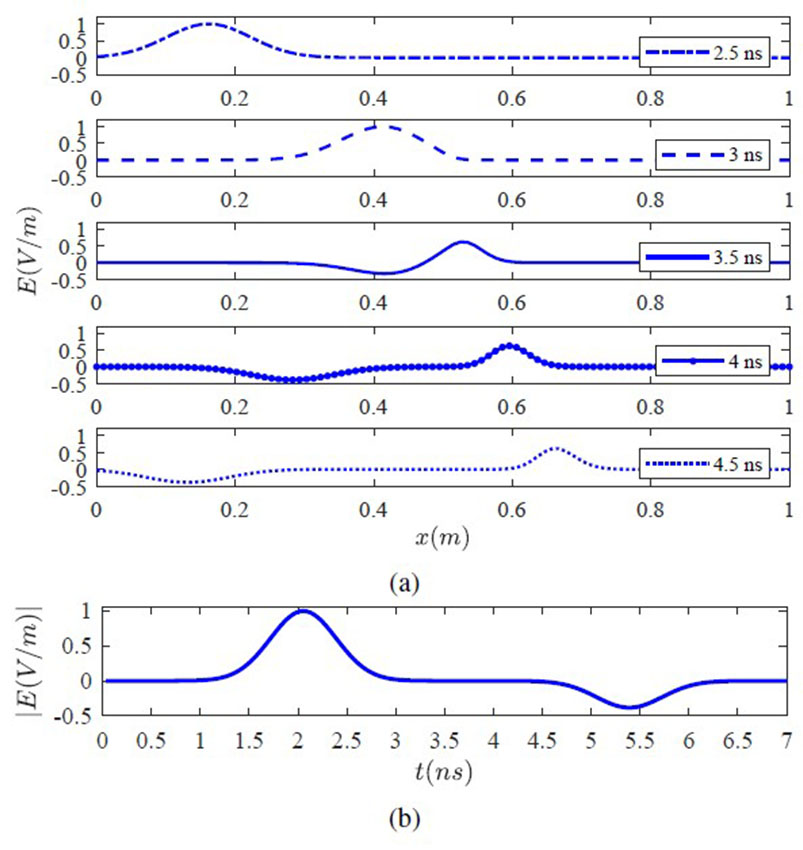 Figure 10 .
Gaussian electromagnetic pulse propagating in air-soil medium: a) at different times, b) radar amplitude profile taken in x0
Figure 10 .
Gaussian electromagnetic pulse propagating in air-soil medium: a) at different times, b) radar amplitude profile taken in x0
Own source
In order to simulate the case when the radar detects a landmine, students must include a PEC boundary condition, 30 cm spaced after the first air-soil discontinuity. The propagating wave in an inhomogeneous media with an air-soil discontinuity and a PEC boundary is shown in Figure 11.
With the amplitude profile shown in Figure 11b, students can first deduce when a landmine is detected and second compute the approximate depth of the explosive object. This setup also helps them answer key questions about landmine detection. For example, i) What happens when landmines are not entirely metallic, and ii) What could be the case when multiple metallic or non-metallic objects are buried apart from the landmine itself. This kind of question opens the discussion about the well-known clutter problem in ground-penetrating radar.
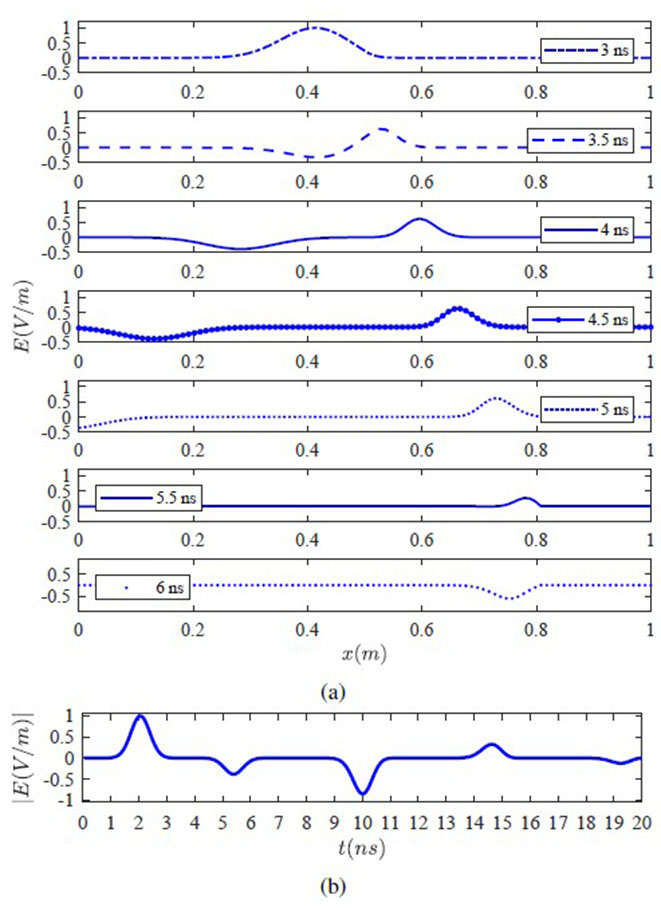 Figure 11 .
Gaussian electromagnetic pulse propagating in air-soil medium with PEC boundary for simulating landmine reflection: a) at different times, b) radar amplitude profile taken in x0.
Figure 11 .
Gaussian electromagnetic pulse propagating in air-soil medium with PEC boundary for simulating landmine reflection: a) at different times, b) radar amplitude profile taken in x0.
Own source
Evaluation methodology and discussion
Data collection procedure
Data collection occurred throughout the last five years (since the first semester of 2015). Each semester, two class sections of the Electromagnetic Transmission course were offered. The course proposal described in this paper (PBL) has been applied to one of the sections, whereas the other section (control group) followed the traditional methodology. The sample population was all the 323 electronic engineering students who finished the Electromagnetic Transmission course. Out of the 323 students, 176 received classes with the proposed methodology, and the remaining 147 students received classes with the traditional methodology. Students are voluntarily enrolled in these groups. However, information about the instructional strategy was not public during class registration.
Methods of data collection
Two types of data were collected. The first one was the final grade and GPA on a scale of 0.0 to 5.0 (passing grade is 3.0). These data were collected for the 323 students.
The second method was a survey distributed in 2015 and 2018 (N=323, response rate=95 %). The survey has three parts. The first part asks students for their perceptions about the difficulty of the course at the beginning and the end. The second part asks about the effectiveness and acceptance of the instructional strategy used. Finally, the third part of the survey inquired about students’ perception of learning some specific course concepts. These surveys were conducted before the students knew their final grade to reduce bias.
Analysis and Discussion
Two types of data were collected. The first one was the final grade and GPA on a scale of 0.0 to 5.0 (passing grade is 3.0). These data were collected for the 323 students.
The second method was a survey distributed in 2015 and 2018 (N=323, response rate=95 %). The survey has three parts. The first part asks students for their perceptions about the difficulty of the course at the beginning and the end. The second part asks about the effectiveness and acceptance of the instructional strategy used. Finally, the third part of the survey inquired about students’ perception of learning in some specific course concepts. These surveys were conducted before the students knew their final grades to reduce bias.
The measurements of central tendency and variability were found using descriptive statistics. The average final grade obtained by the students with the proposed methodology is 3.23, with a variance of 0.42. In contrast, the average obtained by the control group of students was 3.08, with a variance of 0.48. Results of the equality-of-variance test for the two samples (0:73; p > 0:05) confirms the equality of variances. An independent sample t-test was conducted to check the statistical difference in the students’ averages.
Results indicate that there was a statistically significant difference between the average scores for PBL group (M = 3.23, SD = 0.65) and the traditional group (M = 3.08, SD = 0.69); t(331) = 1.967, p < 0:05.
Table 2 shows the corresponding statistical values of each sample, together with the values obtained when performing the t-test.
Table 2 .
Statistical analysis
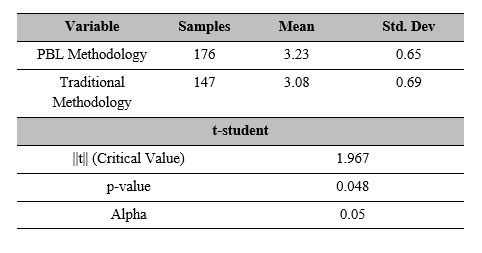
Own source
A paired sample t-test to compare results
The comparison of means was made between each item of the 2015 survey and that of 2018. There were no statistical differences in their results except for two items, which are shown in Figure 12.
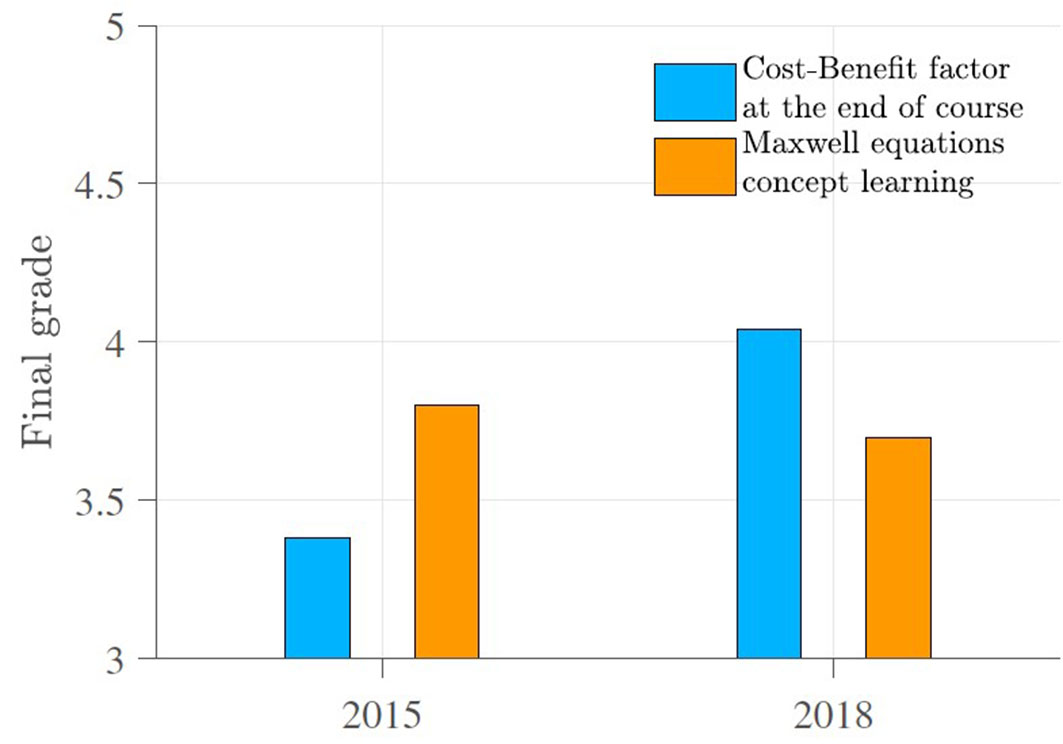 Figure 12
Results comparison between statistically different results
Figure 12
Results comparison between statistically different results
Own source
This indicates that students have perceived an increase in the cost-benefit value of taking the course during the course projects' implementation.
The five most relevant positive results in both surveys are mentioned in Table 3. Regarding the course difficulty perception, the average was higher than 4.17 before taking the course and lower than 3.6 after taking the class in both surveys. It shows a preconception with low favorability about the difficulty of this class, which improved at the end of the class. Although better results are obtained in these two questions in the last survey, there is no statistical difference between these values.
Table 3 .
Survey highest scores in 2015 and 2018

Own source
Additionally, other results have been obtained in terms of the perceived learning about the course subjects. These have remained at the same level except for Maxwell’s Equations, which lowered their rating. More than 80% of the students said that the teacher has been decisive in their perception of the course. Regarding the students’ learning evaluation, more than 82% rated their learning process about electromagnetic wave propagation concepts over 4.0. A similar grade was obtained on Maxwell’s equations and their use. In addition, more than 75% of the total students scored 4.0 or higher on their learning process about the dielectric characteristics of the materials concepts.
Likewise, the three most notorious results that should be improved are:
-
After completing three-quarters of the course, only 35% of the students thought they would pass the course.
-
About 25% of the students scored 2.0 or less, the benefit-cost value of the class.
-
About 30% of the students gave a grade of 2.0 or less for their learning and clarification of concepts about computational numerical methods in electromagnetism, including the project’s utility in the measurement of dielectric properties of materials through a resonant cavity.
In the same way that the highest scores were maintained between the two surveys, the three lowest scores are also maintained in both surveys and correspond to the learning of computational methods, as shown in Table 4.
Table 4 .
Survey lowest scores in 2015 and 2018

Own source
The positive effects perceived in students registered in the PBL class compared to the traditional class were also validated because the GPA of students registered for the traditional class (3.83) was not different from the GPA of students registered for the PBL course (3.81). However, results also indicate that students’ participation in the PBL class did not affect the percentage of students who failed the following course of electromagnetism (Antennas). 21% of the students registered on the PBL course failed the Antennas course later, whereas 20% of the students registered on the traditional course failed the Antennas course later. Nonetheless, there was a slight difference (although not statistically significant) in the percentage of students whose grades were above 4.0 in the Antennas course: 20% of the students registered in the PBL class and 17% of students registered in the traditional methodology class had a final grade above 4.0.
Other elements add to the positive effects perceived in students after implementing the PBL course. Since its inception in 2015, the number of capstone projects related to electromagnetic transmission has increased slightly, as well as the number of students in the elective classes related to these topics (optical transport networks and wireless communications). Also, after 2014, due to the greater interest generated in the students in the area of electromagnetism, students participated in external events and competitions in this area with outstanding results. Among these achievements, the first place obtained in the design, implementation, and operation of an antenna to reception environmental images from the National Oceanic Atmospheric Administration (NOAA) satellites stands out.
Conclusion
A project-based undergraduate course on applied electromagnetics in electronics engineering with a conceiving-designing-implementing-operating (CDIO) approach has been proposed and implemented. In addition, a student survey was carried out showing that students’ perception of the class’s great difficulty affects their learning process since there is a preconception about the course itself even before taking the first lecture. This preconception involves high complexity issues and results in low performance of students. Despite the perceived difficulty of the course, when the students develop the proposed projects under the CDIO working methodology and evidence the application and the development of the concepts covered in class, improvements are evidenced concerning their attitude and learning.
On the other hand, although the applied methodology has been fundamental to reducing the perception of difficulty, and this has improved the learning obtained by the students, not all the projects fulfill these objectives. Especially the resonant cavities project must be evaluated in detail, either by changing its approach or the assessment methods. Nonetheless, the structure of the course aligns very well with the CDIO approach implemented in the Electronic engineering program.
Beyond maintaining the high results about students’ perceptions of difficulty, effectiveness, and acceptance of instructional strategy and learning, data show increased participation in workshops and competitions of applied electromagnetics outside of the university. Hence, continuous work should be promoted and maintained in creating, designing, and implementing more projects related to the applied electromagnetics course and even previous courses, which help demonstrate the application of electromagnetic theory, motivate students, and reduce their perception of the high complexity of the issues.
References
[1] Maxwell, “On the physical lines of magnetic force,” vol. 55, pp. 168–172, 1861.
[2] S. Collier, “Top engineering schools in 2017,” 2019. [Online]. Available: https://www.qschina.cn/university-rankings-articles/university-subject-rankings/top-engineering-schools-2017
[3] David Staelin. 6.013 Electromagnetics and Applications. Spring 2009. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu/courses/6-013-electromagnetics-and-applications-spring-2009/ License: Creative Commons BY-NC-SA.
[4] C S. Ruf and R. Merlin, “Applied electromagnetics and rf circuits,” 2019. [Online]. Available: https://ece.engin.umich.edu/research/research-areas/applied-electromagnetics-rf-circuits/
[5] J. Vuckovic, “Engineering electromagnetics,” 2019. [Online]. Available: https://goo.gl/m1k2ed
[6] E. Yablonovitch, “Electromagnetic fields and waves,” 2019. [Online]. Available: https://goo.gl/sgG57J
[7] Caltech, “Electromagnetic theory,” 2019. [Online]. Available: https://ee.caltech.edu/academics/course_desc.
[8] M. N. O. Sadiku, “Problems Faced by Undergraduates Studying Electromagnetics,” IEEE Transactions on Education, vol. E-29, no. 1, pp. 31–32, 1986.
[9] F. J. Rosenbaum, “Teaching Electromagnetics Around the World: A Survey,” IEEE Transactions on Education, vol. 33, no. 1, pp. 22–34, 1990, https://doi.org/10.1109/13.53624
[10] S. Y. Lim, “Education for electromagnetics: Introducing electromagnetics as an appetizer course for computer science and IT Undergraduates,” IEEE Antennas and Propagation Magazine, vol. 56, no. 5, pp. 216–222, 2014, https://doi.org/10.1109/MAP.2014.6971955
[11] M. L. Lumori and E. M. Kim, “Engaging students in applied electromagnetics at the University of San Diego,” IEEE Transactions on Education, vol. 53, no. 3, pp. 419–429, 2010, https://doi.org/10.1109/TE.2009.2026636
[12] K. Keltikangas and H. Wallén, “Electrical engineers’ perceptions on education - electromagnetic field theory and its connection to working life,” European Journal of Engineering Education, vol. 35, no. 5, pp. 479–487, 2010, https://doi.org/10.1080/03043791003802045
[13] MIT, “Stellar: Mit course management system of electrical engineering and computer science: Electromagnetics applications,” 2019. [Online]. Available: https://stellar.mit.edu/classlink/course6.html
[14] Berkely, “Berkely academic guide: Electromagnetic fields and waves,” 2019. [Online]. Available: https://www2.eecs.berkeley.edu/Courses/EE117/
[15] Stanford, “Stanford bulletin. ExploreCourses: Engineering electromagnetics,” 2019. [Online]. Available: https://explorecourses.stanford.edu/search?q=EE+141%3A+Engineering+Electromagnetics&filter-courses_1
[16] K. F. Warnick, R. Selfridge, and D. V. Arnold, “Teaching Electromagnetic Field Theory Using Differential Forms,” IEEE Transactions on Education, vol. 40, pp. 53–68, 1997, https://hdl.lib.byu.edu/1877/1120
[17] J. B. Temes, “Teaching electromagnetic waves to electrical engineering students: An abridged approach,” IEEE Transactions on Education, vol. 46, no. 2, pp. 283–288, 2003, https://doi.org/10.1109/TE.2002.808275
[18] M. J. Prince and R. M. Felder, “Inductive teaching and learning methods: Definitions, comparisons, and research bases,” Journal of Engineering Education, vol. 95, no. 2, pp. 123–138, 2006, https://doi.org/10.1002/j.2168-9830.2006.tb00884.x
[19] R. M. Felder, H. Celanese, and R. Brent, “Active Learning: an Introduction,” ASQ Higher Education Brief, vol. 2, no. 4, pp. 1–5, 2009. [Online]. Available: https://www.engr.ncsu.edu/wp-content/uploads/drive/1XaOo9WCKcMq6-fTcQGidOT2SDGqg70l5/2009-ALpaper(ASQ).pdf
[20] R. W. Cole, E. K. Miller, S. Chakrabarti, and S. Gogineni, “Learning About Fields and Waves Using Visual Electromagnetics,” IEEE Transactions on Education, vol. 33, no. 1, pp. 81–94, 1990, https://doi.org/10.1109/13.53631
[21] T. Huk, “Who benefits from learning with 3D models? The case of spatial ability,” Journal of Computer Assisted Learning, vol. 22, no. 6, pp. 392–404, 2006. https://doi.org/10.1111/j.1365-2729.2006.00180.x
[22] S. Jayakumaran, “Numerical Approaches to Teaching Electromagnetics: A Historical Sketch and Lessons from Structural Engineering,” IEEE Transactions on Education, vol. 36, no. 2, pp. 265–269, 1993, https://doi.org/10.1109/13.214711
[23] M. Trlep, A. Hamler, M. Jesenik, and B. Stumberger, “Interactive Teaching of Electromagnetic Field by Simultaneous FEM Analysis,” IEEE Transactions on Education, vol. 42, no. 4, pp. 1479–1482, 2006, https://doi.org/10.1109/TMAG.2006.871437
[24] S. Vidal and M. F. Iskander, “Multimedia Modules for Electromagnetics Education,” Computer Applications in Engineering Education, vol. 5, pp. 257–267, 1997, https://doi.org/10.1002/(SICI)1099-0542(1997)5:4<257::AID-CAE5>3.0.CO;2-C
[25] F. Obelleiro, J. M. Taboada, J. L. Rodri, and J. M. Be, “General Purpose Software Package for Electromagnetics Engineering Education,” Computer Applications in Engineering Education, vol. 10, pp. 33–44, 2002. https://doi.org/10.1002/cae.10015
[26] C. Mias, “Electronic Problem Based Learning of Electromagnetics Through Software Development,” Computer Applications in Engineering Education, vol. 16, pp. 12–20, 2008. https://doi.org/10.1002/cae.20112
[27] X. Liu, “A novel teaching platform design with CAI for EM education,” Computer Applications in Engineering Education, vol. 26, pp. 1318–1323, 2018. https://doi.org/10.1002/cae.22026
[28] M. Prince, “Does Active Learning Work? A Review of the Research.” Journal of Engineering Education, vol. 93, no. 3, pp. 223–231, 2004. [Online]. Available: https://www.engr.ncsu.edu/wp-content/uploads/drive/1smSpn4AiHSh8z7a0MHDBwhb_JhcoLQmI/2004-Prince_AL.pdf
[29] J. Macías-Guarasa, J. M. Montero, R. San-Segundo, A. Araujo, and O. Nieto-Taladriz, “A project-based learning approach to design Electronic Systems Curricula,” IEEE Transactions on Education, vol. 49, no. 3, pp. 389–397, 2006. https://doi.org/10.1109/TE.2006.879784
[30] D. H. Jonassen, Engineers as Problem Solvers. Cambridge University Press, 2014, pp. 103-118. https://doi.org/10.1017/CBO9781139013451.009
[31] D. Spikol, E. Ruffaldi, G. Dabisias, and M. Cukurova, “Supervised machine learning in multimodal learning analytics for estimating success in project-based learning,” Journal of Computer Assisted Learning, vol. 34, no. 4, pp. 366–377, 2018. https://doi.org/10.1111/jcal.12263
[32] E. F. Crawley, J. Malmqvist, S. Östlund, and D. R. Brodeur, Rethinking Engineering Education, 1st ed., ser. 1. Springer, 2014, vol. 1. https://doi.org/10.1007/978-0-387-38290-6
[33] CDIO, “The cdio standards 2.0: Standard 7 integrated learning experiences,” 2019. [Online]. Available: https://goo.gl/wqjiaf
[34] CDIO, “The cdio standards 2.0: Standard 8 active learning,” 2019. [Online]. Available: https://goo.gl/rtGd2i
[35] A. Correal, F. Moreno, J. Londoño, K. Renneberg, and F. Sánchez “Active Learning in Electronics Engineering at Pontificia Universidad Javeriana,” in Proceedings of the 12th International CDIO Conference, Turku University of Applied Sciences, Turku, Finland, 2016. [Online]. Available: https://www.cdio.org/knowledge-library/documents/active-learning-electronics-engineering-pontificia-universidad-javeriana
[36] M. Sadiku, Elements of Electromagnetics, 6th ed., ser. 1. Oxford University Press, 2014, vol. 1.
[37] D. K. Cheng, Fundamentals of Engineering Electromagnetics, 1st ed., ser. 1. Pearson, 1992, vol. 1.
[38] J.-M. Jin, Theory and Computation of Electromagnetic Fields, 2nd ed., ser. 1. Wiley-IEEE Press, 2015, vol. 1.
[39] C. A. Balanis, Advanced Engineering Electromagnetics, 1st ed. Wiley, 1989, vol. 1.
[40] C. A. Balanis, Antenna Theory: Analysis and Design, 4th ed. Wiley-Blackwell, 2016, vol. 1.
[41] J.-M. Jin, The Finite Element Method in Electromagnetics, 3rd ed. Wiley-IEEE Press, 2014, vol. 1.
[42] R. F. Harrington, Field Computation by Moment Methods, 1st ed. Wiley-IEEE Press, 1993, vol. 1.
[43] W. C. Gibson, The Method of Moments in Electromagnetics, 2nd ed. Chapman and Hall/CRC, 2014, vol. 1.
[44] K. F. Warnick, Numerical Methods for Engineering: An Introduction Using MATLAB and Computational Electromagnetics, 1st ed., ser. 1. SciTech Publishing, 2011, vol. 1.
[45] S. J. Orfanidis, Electromagnetic Waves and Antennas: Waves, 1st ed., ser. 1. Rutgers university, 2016, vol. 1.
[46] J. Bravo, F. Hurtado and P. A., “Elective Projects Course: Realizing the Academic Interests of Students,” in Proceedings of the 14th International CDIO Conference, Kanazawa Institute of Technology (KIT). Kanazawa Japan, 2018.
[47] J. R. Mosig, “An Old Tool and a New Challenge for Depicting Antenna Array Radiation Patterns,” IEEE Antennas and Propagation Magazine, vol. 53, no. 3, 2011. https://doi.org/10.1109/MAP.2011.6028426
[48] M. N. Afsar, J. R. Birch, R. Clarke, and G. Chantry, “The Measurement of the Properties of Materials,” Proceedings of the IEEE, vol. 74, no. 1, pp. 183–199, 1986. https://doi.org/10.1109/PROC.1986.13432
[49] H. E. Bussey, “Measurement of RF Properties of Materials A Survey,” Proceedings of the IEEE, vol. 55, no. 6, pp. 1046–1053, 1967. https://doi.org/10.1109/PROC.1967.5719
[50] X. Li and Y. Jiang, “Design of a Cylindrical Cavity Resonator for Measurements of Electrical Properties of Dielectric Materials,” Master’s thesis, Glave university, 2010. [Online]. Available: https://www.diva-portal.org/smash/get/diva2:354559/FULLTEXT01.pdfDesign
[51] R. Price, R. Reed, and C. A. Roberts, “Perturbation Theory for Resonant Cavities,” IEEE Transactions on Antennas and Propagation, vol. 11, no. 5, pp. 587–588, 1963. https://doi.org/10.1109/TAP.1963.1138091
[52] G. Birnbaum and J. Franeau, “Measurement of the dielectric constant and loss of solids and liquids by a cavity perturbation method,” Journal of Applied Physics, vol. 20, no. 8, pp. 817–818, 1949. https://doi.org/10.1063/1.1698535
[53] A. R. V. Hippel, Dielectric materials and applications, 1st ed. Artech House Publishers, 1995, vol. 1.
[54] A. Kumar, S. Sharma and G. Singh, “Loss Factor of the Dielectric Material At Microwave Frequencies,” Progress In Electromagnetics Research, vol. 69, pp. 47–54, 2007. https://doi.org/10.2528/PIER06111204
[55] M. Lin and M. N. Afsar, “A new cavity perturbation technique for accurate measurement of dielectric parameters,” in IEEE MTT-S International Microwave Symposium Digest, 2006, pp. 1630–1633. https://doi.org/10.1109/MWSYM.2006.249650
[56] B. Meng, J. Booske, and R. Cooper, “Extended Cavity Perturbation Technique to Determine the Complex Permittivity of Dielectric Materials,” IEEE Transactions on Microwave Theory and Techniques, vol. 43, no. 11, pp. 2633–2636, 1995. https://doi.org/10.1109/22.473190
[57] K. V. Anand Parkash, J and A. Mansingh, “Measurement of dielectric parameters at microwave frequencies by cavity perturbation technique,” IEEE Transactions on Microwave Theory and Techniques, vol. 27, no. 9, pp. 791–795, 1979. https://doi.org/10.1109/TMTT.1979.1129731
Notes
*
Research paper (Artículo de investigación) - Article of scientific and tecnological investigation
Author notes
a Corresponding author. E-mail: manuel.perez@javeriana.edu.co
Additional information
How to cite this article: MR. Pérez-Cerquera, JA. Hurtado-Londoño, JM. Cruz-Bohorquez, “An Applied Electromagnetics Course with a Conceiving-Designing-Implementing-Operating Approach in Engineering Education” Ing. Univ. vol. 26, 2021. https://doi.org/10.11144/Javeriana.iued26.aecw






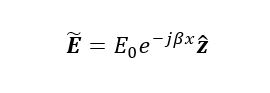 (1)
(1)

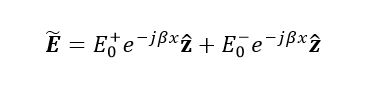 (2)
(2) (3)
(3)
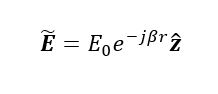 (4)
(4)
 (5)
(5)

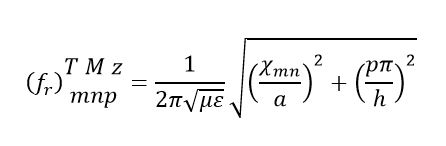 (6)
(6)

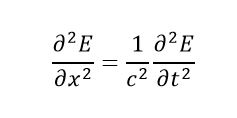 (7)
(7)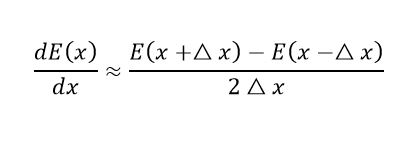 (8)
(8) (9)
(9) (10)
(10)
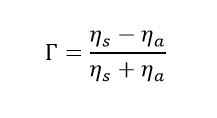 (11)
(11)





