Introduction
The skill of solving engineering-related problems is the skill with the fourth greatest deficit level in recent engineering graduates [1]. In Colombia, the improvement of math learning has been stressed since 1961 [2]. In 1994, the Colombian Ministry of Education restructured the learning model by proposing a set of curricular guidelines based on basic standards of competences and performance assessment [3]. Despite such restructuring, Colombia achieved one of the lowest scores in problem solving out of the 44 countries participating in PISA (Programme for International Student Assessment) [4], [5]. Currently, the government is looking toward internet massification and digital ecosystem development [6] as tools to improve teaching personalization and the opening up of teaching positions based on information access [7].
This problem begins during elementary school and continues during the university level. At the tertiary level, math learning is one of the most relevant issues not only in Colombia but also generally in Latin America [2]. A disconnection between reality and career environment is the main cause [2]; such a disconnection generates high failure indicators in university courses [8]. The implementation of curricular integration, as proposed by CDIO, which connects math and engineering, is a strategy that might contribute to the solution of this problem.
At the global level, different institutions have designed and applied multiple strategies aimed at strengthening math and problem-solving skills using concept integration, which has led to satisfactory outcomes. In this way, the industrial engineering program at Sao Paulo University suggested a model of learning based on engineering implementation projects for first-year students. This model emphasized the role of differential calculus, which resulted in a positive experience [9]. Since 2013, when PBL (project-based learning) was implemented, multiple strategies have been tested, such as activities for improving communication skills and the building and presentation of a real prototype as a solution for the courses’ semesterly works based on real engineering problems. The evidenced evolution has been sufficiently positive such that PBL has been extrapolated to three other engineering programs inside Sao Paulo University [9].
Another alternative for math teaching is computer-based math (CBM), which represents a different method for math teaching that uses machine-computer mathematics in the crucial parts of all curriculums to equip students with tools for applying math in high-level problem solving without thinking about how hard to is to solve such problems by hand [10]. This is a long-term project boosted by Wolfram Research, the developers of Mathematica and Wolfram Alpha software.
Multiple studies that have involved math and engineering teaching methodologies based on computers have resulted in success. For example, the chemistry engineering department of Huelva University in Spain has proposed and implemented a novel teaching methodology for improving the calculation of pumping power by using Mathcad software [11] with second-year chemical engineering students. Surveys applied to these students have indicated that the computational tool and the related training courses highly improved their ability to solve the calculation of pumping power (engineering problem) as the mathematical difficulties were handled by software, which helped them focus on the understanding of the theoretical basis of the phenomenon [11].
Likewise, Kuala Lumpur University improved its engineering students’ understanding of the concepts of integral calculus by means of the integration of the software Maple as an important education tool [12]. The students whose learning was accompanied by this software showed positive results compared to those of their counterparts who took the course that utilized traditional teaching methods. The conceptualization level of the students who used the software was significantly enhanced, allowing them to solve advanced calculus problems related to the determination of areas under functions with multiple roots between a specific study interval. The kindness and facilities delivered by the software with regard to creating and analyzing plots had a positive impact on the understanding of the students [12].
Another success case comes from Putra Malaysia University, where a similar methodology was implemented that combined linear algebra students and Maple software, which produced good results on the understanding of usually hard-to-understand concepts such as eigenvalues and eigenvectors. As the software performed the algebraic manipulations, the students could focus on the important properties and principles of the concepts, thereby improving their understanding [13].
The abovementioned approaches demonstrate real-world math, which requires complex models that should not be approached using hand calculations. However, what is found regarding today’s math education is that 80% of the curriculum time is spent on developing hand-calculation skills focused on algebraic manipulation, even when computer technology is available via math software [14]. This could suggest that engineering students acquire a high-level of expertise for mechanical algebraical processes instead of understanding the background of these complex topics.
Therefore, the aim of this article is to plan and assess a strategy that conjugates curricular integration and CBM for enhancing mathematics learning in mechanical engineering at Santo Tomás University, with a specific focus on engineering problem solving.
Materials and methods
Participants
Sixty-four mechanical engineering students (approximately 15% of the total program population) from Santo Tomás University (Bogotá, Colombia) who were enrolled between their third and eighth semesters took part in this research project. The sample size was determined using Cochran’s formula with a margin of error of 10%, a confidence level of 90%, and a response distribution of 50% of the population size of 430 students, which suggested 59 students for the sample.
Procedure
First, students took a diagnostic test in which they solved four mechanical engineering-related problems. The length of the test was twenty minutes, and the use of computational tools such as Mathematica 11.0 (Wolfram Research, USA) and GeoGebra online (Hohenwarter et al., Austria) was allowed.
Later, the students participated in three practical sessions every two hours, with one study case per session. Each case had a theoretical component developed by the teacher in the first part that was approached by the students using Mathematica 11.0 software. All the theoretical components were analyzed by teachers and students and transformed into a solution process according to math and algorithms. The first step was the understating of the problem and why an optimal answer should be delivered. Then, a theoretical model was involved (Bernoulli’s Principle, for example). After giving test values to some variables, the math model was developed using calculus and algorithms so that the answer could be evaluated to check that all constraints were satisfied. As most engineering problems require an iterative process to achieve a satisfying and optimal answer, the next step was to transform the test values into variables of an iteration so that, via software and forgetting about using hand calculations, the students could execute a programming routine to obtain multiple possibilities and extract the best possible answer to the problem. The result was a Mathematica file with an algorithm designed by each student to solve the problem.
Finally, at the end of each case study session, the students took a test to determine the effect of the methodology on the development of mathematical competences. The questions on and conditions of the final test were similar to those on and of the first test, which allowed us to quantify the math skill development levels using two Bloom’s taxonomy levels of understanding and application.
Diagnostic and final tests
The diagnostic and final tests were made to determine the level of mathematical competence development considering two levels from Bloom’s taxonomy (BT): understanding and application [15]. Each diagnostic test contained four questions linked (one by one) with the subcategories of interpretation, explanation, execution and implementation. In Table 1, the structure of the diagnostic and final tests is displayed.
Table 1.
Structure of diagnostic and final tests
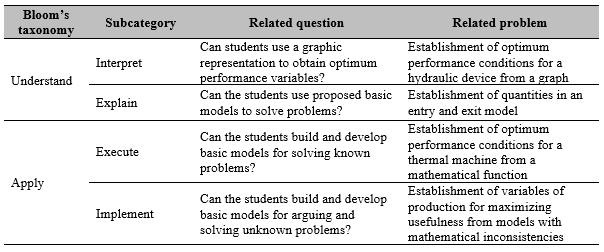
Source: Authors’ own creation.
Study cases
The main purpose of the study cases was to establish a comparison between the traditional methodologies and the new methodologies supported by integrated concepts, with an emphasis on math and software. An introductory case and three main study cases were proposed as a result of the evolution of problems faced by students in three courses of the mechanical engineering program into more complex problems and the creation of alternative solving methods. This transformation was made based on ceratin CDIO standards [16], namely, 3: integrated curriculum, 5: design-implement experiences and 7: integrated learning experience; thus, the new problems allowed students to interact with fundamentals proposed by CDIO.
The problems had been solved by the students in their previous courses using hand calculations. Therefore, a new methodology was built based not only on the previous course concepts but also on math knowledge and programming. Additionally, the study cases were made complex to prevent common functional validations and suggest design problems. As the problems became more complex and traditional methodologies became less helpful, the students focused on building and applying new alternative methodologies that involved not only the concepts learned from a specific engineering course but also their integrated knowledge of math and optimization models. These alternatives were transformed into algorithms with math model implementations that allowed the obtention of fast and optimal answers. All study cases were solved by the students by means of the computer-based math model (CBM), which proposes a step-by-step process of four key stages: problem definition, problem transfer to math, calculation of responses throughout a computer and results interpretation [14], [17].
Introductory case: animation of an airplane take-off
The introductory case was an original idea developed for the current research, and its purpose was to motivate the students to show them how a simple mathematical function and the use of key concepts as derivates are useful for achieving interesting results. The case was presented to all participants regardless of their formation level. The aim of this introductory case study was to foster the students’ interest through an example of a direct mathematical function application resulting from the simplified environment of the traditional calculus courses they had already taken. The students received a set of connected dots that displayed an aircraft’s ascending trajectory (Figure 1). Overall, the take-off is similar to the arctangent function close to the origin. The students used this abstraction to construct an animation in Mathematica 11.0. There, the graphic object of the airplane followed the coordinates (x(t), arctan(x(t))) and inclined according to the curve tangent obtained from the derivative, thereby achieving an optimal representation of the rise.
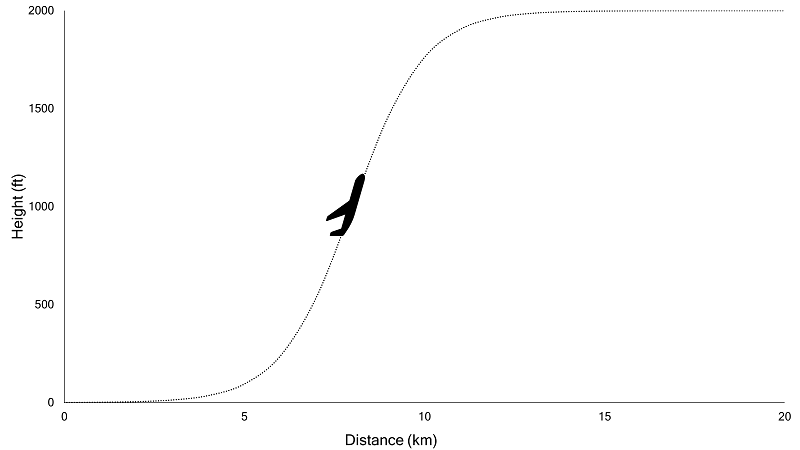 Figure 1.
Airplane take-off animation frame in Case I
Figure 1.
Airplane take-off animation frame in Case I
Source: Authors’ own creation.
Case I: Diameter establishment of a fixed beam of a circular profile bearing a dynamic load
In the second case study, students from the Design of Machine Elements course, which is a junior course available in the seventh semester, determined the minimum diameter of a solid hot-rolled circular profile of 1005 steel in order to guarantee the proposed strength for dynamic loads with a safety factor equal to 1.50 ± 0.05. This tolerance was defined to highlight the differences between calculus and the software given that traditional methodologies lead to solutions with sporadic safety factors, which can hinder the attainment of one-hundredths tolerance [18].
One of the two possible methods of analyzing the system, in accordance with the strength of materials theories, is using singularity functions leading to a two-variable equation (see Equation 1), which expresses the stress that the beam must resist (σ) [18]:
where F is the applied force on the profile at a distance unit from the left support and b distance units measured by the right support, l is the length of the profile, and x is the analysis point.
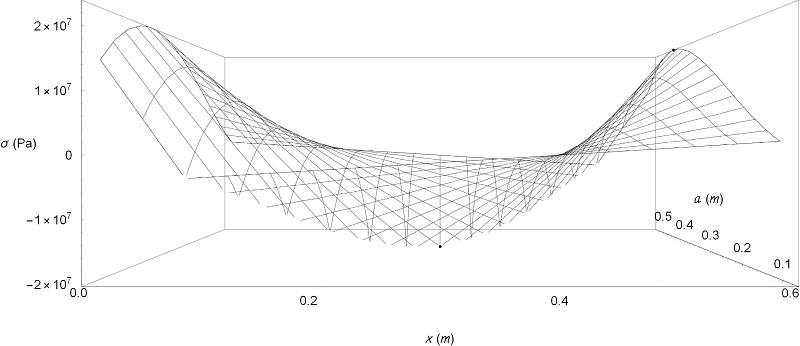 Figure 2.
Maximum and minimum stress points of σ (x, a) (1) obtained by one of the participating students using Mathematica 11.0 for study case 1
Figure 2.
Maximum and minimum stress points of σ (x, a) (1) obtained by one of the participating students using Mathematica 11.0 for study case 1
Source: Authors’ own creation.
Once the function was obtained, the students used the critical points theory in two-variable functions (Figure 2) to find the minimum and maximum stresses, which are the required quantities to determine the material strength for the loads; then, they constructed a programming routine in Mathematica 11.0 for quickly iterating the diameter to achieve the desired safety factor without exceeding the proposed tolerance.
The case study objective was to show the students the differences between calculus and the software with regard to solving difficult problems by comparing the problem-solving achieved using math software with that using manual methodologies. Building an algorithm based on math can simplify any iterative process as a computer iterates itself in accordance with inputs.
The students who wrote and used an algorithm (Figure 3) simply needed to execute the program to obtain the estimated safety factor. If the obtained safety factor did not meet the requirements, the inputs could be changed quickly, and the algorithm could be quickly executed again to get closer to the answer.
 Figure 3.
Part of the code written by one of the participating students in Mathematica 11.0 for the determination of safety factor for study case 1
Figure 3.
Part of the code written by one of the participating students in Mathematica 11.0 for the determination of safety factor for study case 1
Source: Authors’ own creation.
Case II: Hydraulic pump system setup establishment according to experimental data
In this case study, students in the Fluid Mechanics course, which is a sophomore course offered in the fifth semester, established the setup of a hydraulic pump system to transport a specific fluid flow, considering as a basis the experimental data collected by a group of fluid mechanics students for three-phase feed pumps available at the hydraulics laboratory from Santo Tomás University.
In the experimental practice, the upstream and downstream pump pressure, intensity, capability demanded by the three-phase engine and pump shaft angular speed were measured for different flows. The working fluid was water under standard conditions.
The students constructed a simple mathematical model based on the Bernoulli principle (see Equation 2), which they applied to the data to achieve a set of ordered pairs that they related to possible working flows with the hydraulic efficiency device. After applying a polynomial regression in Excel and maximizing the resulting efficiency function using the critical points theory (Figure 4), the participants discussed possible system setups and decided which one would be the best for transporting the amount of required flow in terms of the system efficiency and the operating cost based on the average rate of kWh:
where P is the pressure measured at each analysis point (1 or 2), PB is the power delivered to the fluid because of the pump in terms of pressure head, PL is the power losses because of roughness in terms of pressure heads, V is the speed of the fluid at each analysis point (1 or 2), Z is the height measured from a reference system at each analysis point (1 or 2), g is the gravity acceleration, and rho is the density of the fluid.
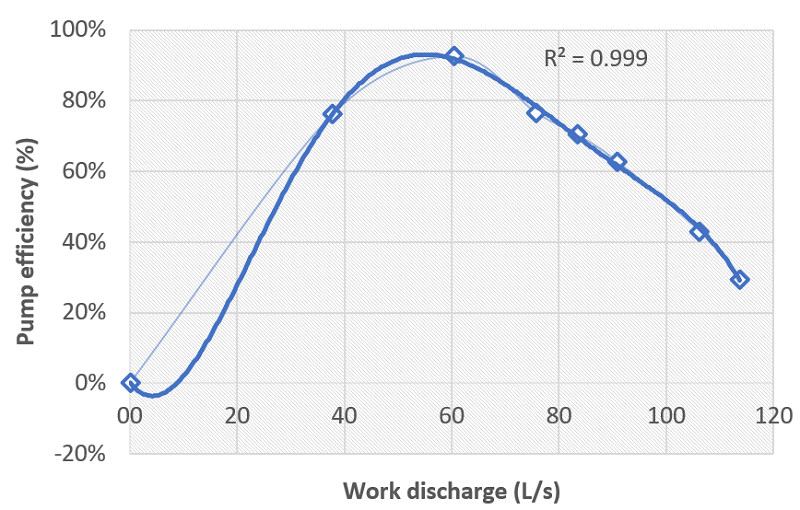 Figure 4.
Efficiency of the pump as a function of work discharge built by one of the participating students using Excel 2016 for determination of process variables in study case 2
Figure 4.
Efficiency of the pump as a function of work discharge built by one of the participating students using Excel 2016 for determination of process variables in study case 2
Source: Authors’ own creation.
This case study required the students to construct a model to solve an engineering-related problem based on their results and group discussion.
Case III: Establishment of the diameter of conductor cable insulation and comparison with real cable
Junior students in their seventh semester must deal with a heat transfer course problem that requires them to find the diameter of an optimum thermal rubber insulation layer for an electric conductor cable, submitted to specific conditions, then compare its outcomes with the diameter measurement of a real cable. Thus, these students developed a model that departed from the Fourier law in cylindrical coordinates [19] (Equation 3) to establish the diameter of the thermal insulation layer that in accord with the theory, guaranteed the best condition for heat transfer. Later, they measured the diameter of the real cable using a slide gauge by themselves, showing a match between the results reached via the mathematical model (Figure 5) and the real cable dimensions:
This case study required the students to arrive at the same solution of a real problem provided by the industry through mathematical modeling using differential geometry and differential equations.
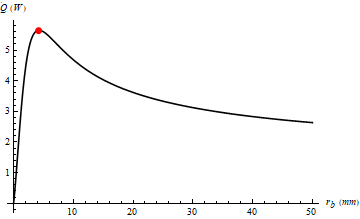 Figure 5.
Heat transfer curve for a conduct cable as a function of the thermal insulating layer radius obtained by one of the participating students using Mathematica 11.0 for study case 3
Figure 5.
Heat transfer curve for a conduct cable as a function of the thermal insulating layer radius obtained by one of the participating students using Mathematica 11.0 for study case 3
Source: Authors’ own creation.
Results and analysis
Diagnostic input test
The diagnostic input test showed that 72% of the students used a graphic representation to obtain optimum performance variables. Out of 64 participants, 46 identified the point in a curve, graphically represented in the plane as the result achieved via the optimum performance system. Nonetheless, only 15% of the students (7) who identified the optimal point in the graph, when faced with a similar problem without graphic representation, were able to construct and develop a mathematical model that allowed them to obtain the optimum performance variables (Figure 6).
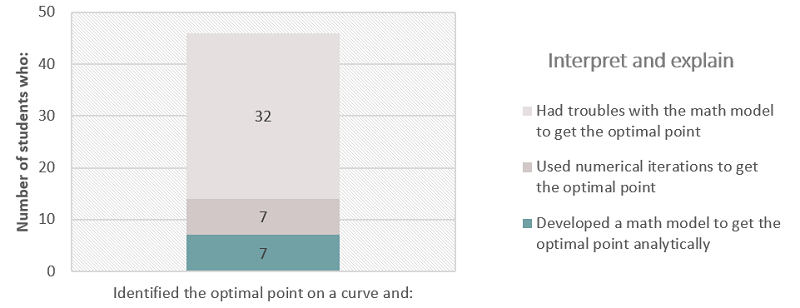 Figure 6.
Interpret and explain indicator quantification.
Figure 6.
Interpret and explain indicator quantification.
Source: Authors’ own creation.
On the other hand, 55% of the students (35) utilized simple mathematical models posed by the test to solve a problem. However, only 13% of the participants (8) were able to construct and develop a mathematical model that permitted them to attain the best response, even surpassing the mathematical inconsistencies related to the unknown environment they were facing (Figure 7).
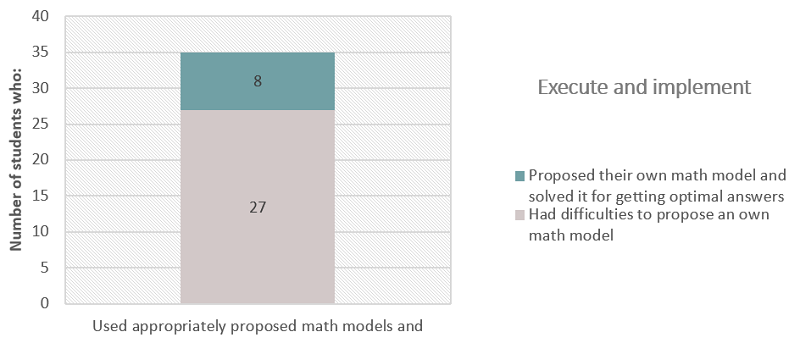 Figure 7.
Execute and implement indicator quantification.
Figure 7.
Execute and implement indicator quantification.
Source: Authors’ own creation.
Difficulties found
The diagnostic input test and subcategories from the second level of Bloom’s taxonomy allow us to identify the main difficulties presented by students when solving engineering problems.
As 72% of the students properly obtained the optimum performance variables using a graphic representation, it is possible to say that most of the students have a suitable level of the interpret skill. This allows them to transform the way in which they represent the information, as they took graphical quantities and converted them into numerical values. However, only 15% of the students who have an appropriate level of the interpret skill (11% of the total number of students) were found to have an adequate level of the execution skill. Even with proper interpretation skills, most of the students could not build and solve a mathematical model to obtain the same answers as those obtained via graphics. When the students did not have graphical support and were challenged to prepare their own model for obtaining optimal solutions for a known problem, their weakness appeared.
When the students had an already proposed model, the results were much better than when they had to build and solve such a model. Fifty-five percent of the students correctly managed the proposed models well enough to solve the problem. Thus, it is possible to assert that half of the students have a proper level of the explain skill, as they used already proposed math models to solve problems. Nonetheless, only 13% of the students could build and calculate their own math model for unknown problems. Therefore, only 13% of the students demonstrated an accurate level of the implement skill. When comparing this result with the that related to the execute skill, the following question arises: why does solving unknown problems look easier than already known problems?
In summary, most of the students from the mechanical engineering program had good interpreting skills, while half of the students showed good explaining skills; in contrast, only 13% showed good implementation skills, while only 11% displayed good execution skills.
The test design allows us to see the level of achievement but does not identify the reason for failure if the problem is not adequately addressed. As an improvement recommendation for subsequent studies, it is proposed to not only ask open-ended questions but also give the students statements that present the problem accompanied by various items regarding the same statement. These items can inquire about how the problem-solving process is carried out and where it fails. For example, a standardization phase for the solution process can be used, as discussed in [20]. To assess whether in the initial phase there has been an understanding of the problem, one could ask the following questions: “What is the unknown or output variable? What data do I have and what data do I need? What and how is the condition?” In the final phase, questions such as “In what other problems can I apply this result or procedure?” are useful for identifying if the application level in Bloom´s taxonomy has been achieved.
In addition, this type of study should also ask about the motivation of the students at the time of assessment. It is possible that a low performance level is conditioned not only by an insufficient foundation or the lack of adequate tools to solve a specific problem but also by a low level of motivation on behalf of the subject. Perhaps students do not consider the evaluated subject important for their professional performance, or they find the test unconnected with the course in which it is applied [21], [22]. Some authors estimate that there is a better performance and use of computational tools when they are used in specific domains and personally relevant contexts [23].
Evaluation output test
After the three practical sessions, the final test evidenced a satisfactory increase in the percentage number of students who used graphic representation to obtain optimum performance variables (93%). Furthermore, 62% of the students identified the point properly and constructed and developed a mathematical model that allowed them to obtain optimum performance variables in a second problem.
Similarly, despite the decrease in students who used a simple proposed mathematical model (44%), the number of participants who satisfactorily faced an unknown problem related to mathematical inconsistencies by constructing and developing their own models increased to 26%.
The following plot compares the outcomes of both the diagnostic input and output tests, according to the related subcategories and in accordance with Bloom’s taxonomy (Figure 8).
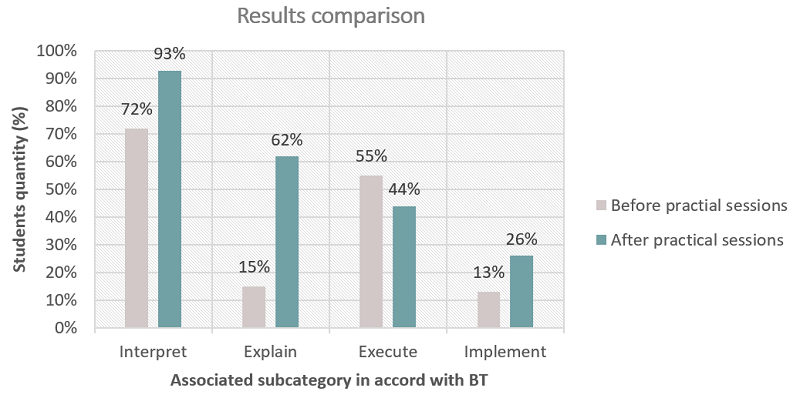 Figure 8.
Comparison between indicators before and after practical sessions
Figure 8.
Comparison between indicators before and after practical sessions
Source: Authors’ own creation.
Analysis
Significantly, most of the participants (93%) were shown to have skills in using graphic representations for obtaining optimum solutions in comparison with the initial finding of 72%. This indicator illustrates an increase in the students’ interpretative capacity since they are shown to have transformed the way in which they represent information to fit better within problem-solving activities. Likewise, the meaningful increase in the number of participants who utilized the models proposed for problem solving (47%) shows an improvement in students’ competence level with regard to explanation, owing to the use of tools related to the concepts of integration and computation. In turn, the fourth indicator shows that students enhanced their skill level in solving unknown problems in manner that departs from posing and developing a mathematical model (implementation). However, the number of handicaps related to solving known problems using the proposal and development of a mathematical model (execute) increased.
The enhancement of interpretation and explanation skills is translated, in accordance with BT, into an increase in students’ capacity to understand the concepts and therefore the problems. The three practical sessions made it possible to enhance this skill in the group of students. Additionally, the fact that the students showed greater skill in facing new problems rather than working with previously known problems, demonstrates how the students welcomed the proposed methodology in the practical sessions while the traditional method was relegated to the background.
This finding proves that teaching methodologies that include multidisciplinary concepts of integration and software to replace algebraical manipulation can result in good levels of development of student’s skills related to interpreting, explaining and implementing key abilities for facing and solving unknown engineering problems. The methodology proposed within this investigation represents the conjunction of the good results obtained by the enforcement of CDIO standards 3, 5 and 7 in real cases of PBL being applied at Sao Paulo University with the advantages of CBM learning in order to achieve successful understanding, as evidenced at Huelva University; this methodology is also empowering as it is not limited to a single math course but rather applicable to the development of problem-solving skills within any engineering challenge.
On average, for the different categories of Bloom's taxonomy shown in Figure 8, the results improved by 45%. This outcome indicates that the use of mathematics software may give better learning results than simulation software, especially when comparing the findings of this study with those of Dickerson and Clark [24]. Furthermore, mathematics software can be used in multiple subjects, while simulation software, due to its complexity and specificity, can be applied only in a few engineering courses. That is, the cost of investment in mathematics software can be lower and useful in more courses than obtaining a single simulation software for automation with pneumatics and hydraulics, another for thermodynamics, another for electronics and so on. This is not because simulation software is not useful; however, when embarking on the journey of software-supported learning, mathematics software may offer more value for money in a first stage.
In the developed study, it can be seen how software can be used at different stages of the formation process. In the introductory case, using a real situation that can be modeled using both a mathematical function and the software helps students to visualize data. This corresponds to the levels of understanding and application of BT. The case of the fixed beam makes use of iterative trial and error operations where a possible answer to a problem is executed and examined according to the application and evaluation levels of BT. The case of the pump bank shows how a combined use of software can help one to understand and use what has been seen in laboratory practices, which has been proposed by other authors [14], [17], [20]. Finally, the case of cable insulation shows the usefulness of using software in the solution of differential equations that often appear in engineering problems but are usually difficult to solve by manual methods. This case also considers the application and evaluation level of BT.
Conclusions
Participating students demonstrated the empowerment of their skills for solving unknown engineering problems when they were introduced to new strategies related to the integration of different concepts from engineering sciences and basic sciences that emphasized math and were supported by specialized computational technologies.
Fifty-six percent of the students showed that they had enough problem-solving skills in accordance with the final test results, compared with the 38% evidenced in the diagnostic test, resulting in a satisfying improvement of 18%. Thus, the use of curricular integration, design-implement practices, and integrated learning experiences as strategies for engineering teaching, combined with the interactive use of specialized math software for problem solving, can result in the improvement of students’ interpretation, explanation and implementation skills for problem solving.
These results open up possibilities for new teaching methodologies in which engineering formation courses use math software tools as a key feature for learning, which can play a fundamental role in developing problem-solving skills.
References
[1] H. L. Saavedra Guevara and Y. T. Vega Hernández, “Evaluación de la calidad de la formación de los graduados de los programas de pregrado de la UPB seccional Bucaramanga, desde la perspectiva de los empleadores,” Universidad Pontificia Bolivariana, 2014.
[2] G. García, “Reformas En La Enseñanza De Las Matemáticas Escolares: Perspectivas Para Su Desarrollo,” Rev. EMA, vol. 1, no. 3, pp. 195–206, 1996.
[3] M. Murcia and J. Henao, “Mathematics education in Colombia, an evolutionary perspective,” Entre Cienc. e Ing., vol. 9, no. 18, pp. 23–30, 2015, doi: https://doi.org/10.1016/S0301-9322(03)00081-8
[4] National Center of Education Statistics, “Data Point: Problem Solving Skills of 15-Year-Olds: Results from PISA 2012,” 2014.
[5] OECD, PISA 2012 Results : Creative Problem Solving: Students’ Skills in Tackling Real-Life Problems, vol. V. OECD Publishing, 2012.
[6] Gobierno de Colombia - MinTIC, “El Plan Vive Digital,” Ministerio de Tecnologías de la Información y Comunicaciones, 2014. .
[7] Gobierno de Colombia - MinTIC, “TIC y educación,” Ministerio de Tecnologías de la Información y Comunicaciones, 2014. .
[8] P. Caramena Gallardo, “Aportaciones de Investigación al Aprendizaje Y Enseñanza de la Matemática en Ingeniería,” 2010.
[9] M. A. C. Pereira, M. A. M. Barreto, and M. Pazeti, “Application of Project-Based Learning in the first year of an Industrial Engineering Program: lessons learned and challenges,” Production, vol. 27, no. spe, pp. 1–13, 2017, doi: https://doi.org/10.1590/0103-6513.223816
[10] Computer Based Math Org., “Learn about the Initiative towards Computer-Based Maths Education,” 2014.
[11] A. A. Cuadri, J. E. Marín-Alfonso, and J. Urbano, “A teaching methodology based on Mathcad for improving the calculation of pumping power,” Educ. Chem. Eng., 2018, doi: https://doi.org/10.1016/j.ece.2018.11.007
[12] T. Salwani Salleh and E. Zakaria, “The effects of maple integrated strategy on engineering technology students’ understanding of integral calculus,” Turkish Online J. Educ. Technol., vol. 15, no. 3, pp. 183–194, 2016.
[13] A. Kilicman, M. A. Hassan, and S. K. S. Husain, “Teaching and learning using mathematics software ‘the new challenge,’” Procedia - Soc. Behav. Sci., vol. 8, pp. 613–619, 2010, doi: https://doi.org/10.1016/j.sbspro.2010.12.085
[14] A. Titterton and Computer Based Method Org., “Making the Case for Computer-Based Maths Education,” 2014.
[15] F. Radmehr and M. Drake, “An assessment-based model for exploring the solving of mathematical problems: Utilizing revised bloom’s taxonomy and facets of metacognition,” Stud. Educ. Eval., vol. 59, no. July 2017, pp. 41–51, 2018, doi: https://doi.org/10.1016/j.stueduc.2018.02.004
[16] CDIO, “CDIO Standard 2.1 | Worldwide CDIO Initiative,” Worldwide CDIO Initiative, 2016.
[17] S. Kadry and M. El Shalkamy, “Toward New Vision in Teaching Calculus,” IERI Procedia, vol. 2, pp. 548–553, 2012, doi: https://doi.org/10.1016/j.ieri.2012.06.132
[18] R. Budynas and K. Nisbett, Shigley’s Mechanical Engineering Design, 10th ed. New York: MC GRAW HILL, 2013.
[19] A. Cengel Yunus, Heat Transfer: A Practical Approach, Higher Edu. MC GRAW HILL, 2002.
[20] T. Tambychik and T. S. M. Meerah, “Students’ difficulties in mathematics problem-solving: What do they say?,” in Procedia - Social and Behavioral Sciences, Jan. 2010, vol. 8, pp. 142–151, doi: https://doi.org/10.1016/j.sbspro.2010.12.020
[21] S. Abramovich, A. Z. Grinshpan, and D. L. Milligan, “Teaching Mathematics through Concept Motivation and Action Learning,” Educ. Res. Int., vol. 2019, 2019, doi: https://doi.org/10.1155/2019/3745406
[22] M. J. N. Mendezabal and D. J. C. Tindowen, “Improving students’ attitude, conceptual understanding and procedural skills in differential calculus through Microsoft mathematics,” JOTSE, ISSN-e 2013-6374, Vol. 8, No. 4, 2018, págs. 385-397, vol. 8, no. 4, pp. 385–397, 2018, Accessed: Jul. 11, 2021, doi: https://doi.org/10.3926/jotse.356
[23] A. J. Magana and G. Coutinho, “Modeling and Simulation Practices for a Computational Thinking-Enabled Engineering Workforce Computational science and Computational thinking education View project Haptic-based Learning Experiences as Cognitive Mediators for Conceptual Learning and Representational Competence View project,” 2016, doi: https://doi.org/10.1002/cae.21779
[24] S. J. Dickerson and R. M. Clark, “A classroom-based simulation-centric approach to microelectronics education,” Comput. Appl. Eng. Educ., vol. 26, no. 4, pp. 768–781, Jul. 2018, doi: https://doi.org/10.1002/cae.21918
Author notes
a Corresponding author. E-mail: mavelascop@udistrital.edu.co
Additional information
How to Cite: N. Góngora, D. Malagón-Romero and, M. A. Velasco, “Assessment of using software for the acquisition of problem-solving skills in mechanical engineering students” Ing. Univ. vol. 26, 2022. https://doi.org/10.11144/Javeriana.iued26.ausa







 (1)
(1)

 (2)
(2)
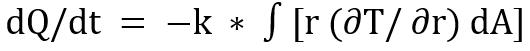 (3)
(3)



