Introducción
En la actualidad existe un gran interés en dotar con autonomía energética y movilidad a los dispositivos electrónicos, y así permitir la implementación de algunos conceptos tecnológicos novedosos como: el internet de las cosas [1] y las redes inalámbricas corporales [2], [3]. Por ejemplo, los nodos implantados de una red corporal podrían funcionar sin usar baterías, usando sistemas de transferencia de energía inalámbrica (WPT, por sus siglas en inglés) que usen las fuentes de energía presentes sobre el cuerpo humano [4], [5], como se ilustra en la Figura 1a. Como otro ejemplo, los teléfonos celulares consiguen dicha autonomía y movilidad a través de cargadores inalámbricos basados en enlaces inductivos (IL, por sus siglas en inglés) [6]. Estos enlaces son comúnmente usados en sistemas WPT, porque el campo electromagnético queda confinado en una región del espacio próxima al sistema [6]. Un IL está compuesto por dos bobinas acopladas magnéticamente, que son diseñadas para maximizar la eficiencia del sistema sujeto a las restricciones propias de cada aplicación [4], [7], [8].
La eficiencia de un enlace inductivo se puede expresar como [8] (ecuación 1)
donde, kIL es el coeficiente de acoplamiento del enlace, A es el nivel de acoplamiento del enlace, y QTx(Rx) son los factores de calidad de las bobinas transmisora (Tx) y receptora (Rx) de energía. En [8], se maximiza el factor A para maximizar la eficiencia del enlace con un receptor con serias restricciones de factor de forma. Los autores proponen el uso de inductores cuadrados planares de una vuelta (PSOI, por sus siglas en inglés), cuya geometría se ilustra en la figura 1b. Esta geometría permite que los inductores sean fácilmente integrables y maximizar simultáneamente el factor de calidad de los inductores implementados y el kIL del enlace. Para optimizar la eficiencia del enlace, los autores maximizaron, en simulación de onda completa, cada componente del factor A (i. e., kIL, QTx, QRx) individualmente.
Para disminuir el costo computacional asociado a este proceso de diseño, en [9], se propuso optimizar el factor A, usando un modelo analítico de los PSOIs y la técnica de programación geométrica. Esta aproximación, permite usar la simulación de onda completa solamente como herramienta de validación, antes de las fases de prototipado y verificación experimental. Sin embargo, el modelo de PSOI usado limita la optimización del enlace, porque subestimaba el factor de calidad (Q) del inductor cerca de su frecuencia de autorresonancia (SRF, por sus siglas en inglés).
 Figura 1a.
Inductores cuadrados planares de una vuelta (PSOI). a) Para alimentar implantes.
Figura 1a.
Inductores cuadrados planares de una vuelta (PSOI). a) Para alimentar implantes.
Fuente: elaboración propia.
 Figura 1b.
Inductores cuadrados planares de una vuelta (PSOI). b) Geometría.
Figura 1b.
Inductores cuadrados planares de una vuelta (PSOI). b) Geometría.
Fuente: elaboración propia.
En un enlace asimétrico optimo, la bobina transmisora opera cerca de su frecuencia de autorresonancia (SRF, por sus siglas en inglés) [10], generando que su factor de calidad aparente (Qa) no sea una buena estimación de su factor de calidad [11], este factor está definido como:
donde, Ze es la impedancia de entrada del inductor. La mayoría de modelos de inductores planares reportados en la literatura son sintetizados usando Qa, y consecuentemente subestiman del factor de calidad (Q) en frecuencias cercanas a la SRF del inductor [12]. Es decir, a pesar de que el modelaje de inductores es un tema ampliamente abordado en la literatura, existe una necesidad de modelos que sean capaces de estimar el valor del Q con precisión hasta la SRF del inductor, especialmente en aplicaciones de WPT con cargas miniaturizadas. En [13], se propuso un modelo analítico de PSOI que estima, con bajo error, el valor de su Ze y Q, de los inductores, hasta cerca de su SRF.
Este artículo propone y evalúa un modelo analítico de enlaces inductivos asimétricos basados en PSOI. Este modelo se basa en el modelo de los PSOIs propuesto por [13] el cual es expandido usando una expresión analítica para la inductancia mutua, propuesta por [14]. La combinación de estas propuestas permite generar un nuevo modelo analítico de enlaces inductivos que permite capturar con bajo error sus dinámicas, incluso cuando sus inductores operan cerca de sus autorresonancias. Este modelo novedoso es evaluado usando simulación electromagnética de onda completa y experimentalmente. Para medir el factor A se usó la ecuación analítica propuesta por [15]. Los resultados evidencian que el modelo estima consistentemente la eficiencia y el factor A del caso de estudio analizado en este artículo. El resto del artículo se organizó de la siguiente manera: en la sección II se discute de forma corta el modelado de inductores para aplicaciones WPT. La sección III describe el modelo propuesto el cual es evaluado en la sección IV. En la sección V, son descritos los resultados de la evaluación del modelo y se hacen algunas recomendaciones para trabajos futuros. Finalmente, en la sección VI se presentan las conclusiones y las contribuciones de este trabajo.
Modelado Inductores para WPT
A pesar de que los inductores son sistemas distribuidos, generalmente se modelan mediante circuitos equivalentes de parámetros concentrados [16]. Para aplicaciones de WPT, los desarrolladores usan circuitos eléctricos para modelar los inductores reales, los más usados son ilustrados en la Figura 2. Los parámetros del modelo RL se pueden calcular como:
donde, f es la frecuencia eléctrica. Este modelo, es comúnmente usado por que sus parámetros pueden extraerse con facilidad de las medidas experimentales. Sin embargo, estima con baja precisión el factor de calidad del inductor, cuando el opera cerca de su SRF [11]. El modelo RLC es ampliamente usado para modelar los inductores en los ILs [9],[14],[15],[17], ya que permite una mejor comprensión de la física del inductor al separar la autorresonancia, de los fenómenos inductivos y resistivos [11]. En este modelo, Lp representa tanto la autoinducción del cable como la inductancia mutua distribuida de la bobina. Por su parte, Cp representa la autocapacitancia del cable y la capacitancia distribuida de la bobina. Cuando el dispositivo opera cerca de su SRF, los fenómenos inductivos y capacitivos distribuidos son no uniformes y se vuelven dependientes de tanto de la frecuencia como de la posición. Finalmente, Rp modela la resistencia asociada a los conductores con los que se fabrica el dispositivo, dicho parámetro está determinado por varios fenómenos físicos (i. e., efecto de piel, efectos de apiñamiento de la corriente, corrientes de Foucault, radiación, etc.). Estos parámetros se calculan para ajustar el modelo a los datos experimentales usando técnicas numéricas. Comúnmente, para simplificar el modelo, los parámetros Lp y Cp se consideran constantes con la frecuencia, debido a que su variación es mucho menor que la del parámetro del Rp.
Cuando el modelo RLC o LR son usados para modelar los inductores de un IL, se considera que la teoría convencional de inductores acoplados permite modelar la transferencia de energía entre las bobinas, las cuales son modeladas por los inductores ideales (i. e., Lp o Ls) de los modelos circuitales. Para analizar la relación entre estos modelos y el factor de calidad de los inductores se discutirá brevemente el concepto de factor de calidad usado en aplicaciones WPT y evitar así confusiones producto de las múltiples expresiones del factor de calidad (Q) en diferentes contextos [18].
 Figura 2a.
Modelos circuitales de inductores para aplicaciones WPT (PSOI). a) Modelo RL.
Figura 2a.
Modelos circuitales de inductores para aplicaciones WPT (PSOI). a) Modelo RL.
Fuente: elaboración propia.
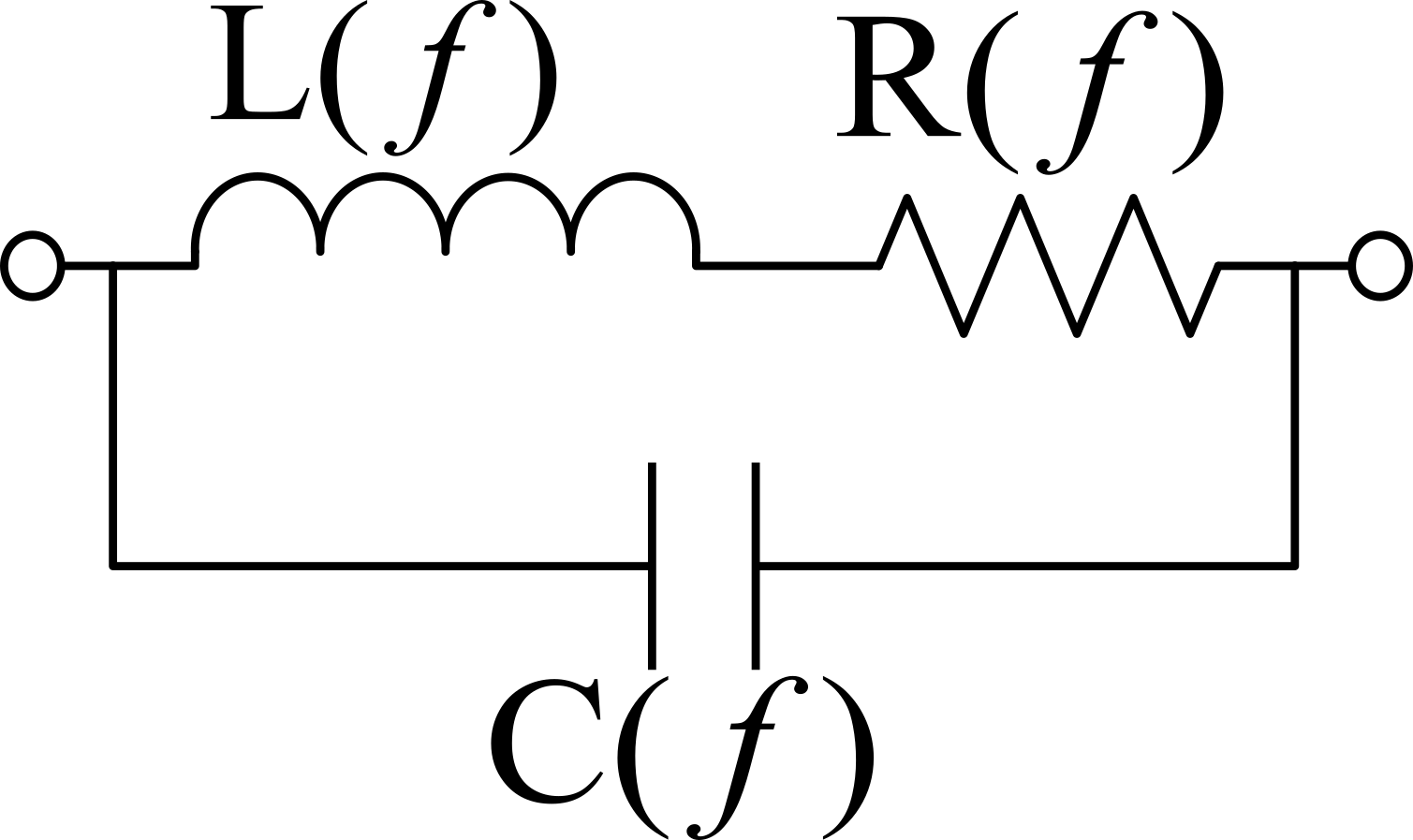 Figura 2b.
Modelos circuitales de inductores para aplicaciones WPT (PSOI). b) Modelo RLC.
Figura 2b.
Modelos circuitales de inductores para aplicaciones WPT (PSOI). b) Modelo RLC.
Fuente: elaboración propia.
El factor de calidad de un inductor describe el dispositivo como un elemento de almacenamiento de energía [19]. La definición más general del factor Q viene dada por [11]:
donde WM, y WE son las energías magnética y eléctrica promedio almacenadas en el inductor, Wmax es la energía máxima almacenada, y Wdiss es la energía promedio disipada por el dispositivo. La estimación del QEmax usando Qa puede ser adecuada solo para frecuencias muy inferiores a la SRF del inductor [11],[12]. Por ejemplo, si el inductor opera en su SRF WM=WE, y por lo tanto la energía total es cero, lo que significa que el QEmax estimado utilizando Qa es cero, este resultado es físicamente irrazonable. Desde el punto de vista del circuito, cuando el inductor se modela utilizando el modelo RL, su Q viene dado por:
donde ω es la frecuencia angular de la señal eléctrica. Por otro lado, cuando el inductor se modela utilizando el modelo RLC, su Q es:
El modelo propuesto en este artículo se basa en un circuito RLC, y se notaran los parámetros de dicho modelo como L, C y R en lugar de Lp, Cp y Rp, por simplicidad en la notación.
Modelado del Enlace Inductivo
En esta sección se resume el modelo de PSOI propuesto. Para modelar los inductores PSOI se usó el modelo RLC propuesto en [13]:
Donde μ es la permeabilidad magnética, ε es la permitividad eléctrica, y ρ es la resistividad del conductor. Las variables α1, β1 y β2 son parámetros del modelo que permiten ajustar el mismo a la tecnología usada en la fabricación del inductor. A partir del modelo RLC resultante y usando análisis de circuitos, se puede estimar SRF, Ze y Q del PSOI como:
Para modelar la transferencia energética del enlace inductivo, se usó la expresión propuesta en [14],[15]:
donde Kγ(γ) y Eγ(γ) son las integrales elípticas complejas de primer y segundo orden, respectivamente, cuyo argumento γ, se expresa como:
donde, d es la distancia entre la bobina transmisora y la receptora, asumiendo que están completamente alineados en sus centros, davg1 y davg2 son parámetros geométricos de los PSOI. A partir de (14) y (8) el coeficiente de acoplamiento del enlace está dado por:
Es importante notar que el modelo compuesto por las ecuaciones (8), (9), (10) y (16) es un nuevo modelo analítico de enlaces inductivos asimétricos basados en inductores PSOIs, que integra dos propuestas reportadas en la literatura para modelar con alta precisión la operación de los enlaces inclusive cuando sus inductores operan cerca a sus SRFs. Hasta el buen entendimiento de los autores, no se tiene otro modelo circuital para enlaces inductivos que permita capturar la trasferencia de energía cuando uno (o los dos) inductores del enlace operan cerca a sus SRFs.
Evaluación del Modelo Propuesto
Como caso de estudio para la evaluación del modelo propuesto en la sección anterior, se usó el enlace inductivo basado en inductores PSOIs con los parámetros geométricos resumidos en la Tabla 1, los cuales se encuentran separados por 15 mm y fueron fabricados en substrato FR4, por lo tanto, los parámetros del modelo usados fueron [13]: α = 128, β1 = 0.3 y β2 = 0.1. El montaje experimental del caso de estudio propuesto se presenta en la Figura 3a. Todas las medidas se realizaron en un ambiente de laboratorio debido a que al estar contenidos los campos no es necesario un ambiente totalmente controlado como una cámara anecoica. En todos los montajes experimentales discutidos en esta sección, fueron usados conectores U.FL. para la conexión eléctrica con el VNA de los dispositivos bajo prueba. Para calibrar el VNA (i. e., two ports R&SR ZVB8), se diseñó e implemento un kit U.FL. de calibración basado en el estándar SOLT (i. e., Corto, abierto, Carga y Directo) en substrato FR4, el cual se ilustra en la figura 3b.
Tabla 1.
Parámetros Geométricos de los PSOI del Caso de Estudio

Fuente: elaboración propia.
 Figura 3a.
Percepción de la participación en clase. a) Montaje experimental.
Figura 3a.
Percepción de la participación en clase. a) Montaje experimental.
Fuente: elaboración propia.
 Figura 3b.
Percepción de la participación en clase. b) Kit de calibración U.FL.
Figura 3b.
Percepción de la participación en clase. b) Kit de calibración U.FL.
Fuente: elaboración propia.
 Figura 3c.
Percepción de la participación en clase. c) Circuito equivalente.
Figura 3c.
Percepción de la participación en clase. c) Circuito equivalente.
Fuente: elaboración propia.
Factor de calidad de los inductores del enlace
Para verificar experimentalmente la capacidad del modelo para predecir el factor de calidad de los PSOIs cerca de su SRF, se caracterizó el inductor transmisor del caso de estudio. Este inductor opera en una frecuencia cercana a su SRF, y se caracteriza por un Q elevado. Para superar los desafíos experimentales presentes en este tipo de mediciones se usó el método propuesto en [10], que se basa en un sensor un inductivo con una SRF mucho mayor que el inductor bajo prueba, el cual es caracterizado a partir de sus parámetros de dispersión medidos. Posteriormente, se estima el factor de calidad del inductor bajo prueba a partir de la caracterización del enlace inductivo fuertemente acoplado (i. e., KIL elevado) entre el sensor y el inductor bajo prueba. El montaje experimental de la caracterización del inductor transmisor del caso de estudio se ilustra en la figura 4.
 Figura 4a.
Percepción de la participación en clase. a) Inductor bajo prueba.
Figura 4a.
Percepción de la participación en clase. a) Inductor bajo prueba.
Fuente: elaboración propia.
 Figura 4b.
Percepción de la participación en clase. b) Sensor.
Figura 4b.
Percepción de la participación en clase. b) Sensor.
Fuente: elaboración propia.
 Figura 4c.
Percepción de la participación en clase. c) Inductor y sensor acoplados.
Figura 4c.
Percepción de la participación en clase. c) Inductor y sensor acoplados.
Fuente: elaboración propia.
En la figura 5, los resultados experimentales del factor de calidad del inductor transmisor son comparados en su valor teórico y simulado. El factor de calidad teórico se calculó usando un script de MATLAB® (MATrix LABoratory), el cual implementaba el modelo propuesto. Por su parte, el factor de calidad simulado fue calculado a partir de los parámetros de dispersión resultantes de su simulación electromagnética de onda completa implementada en el software Electromagnetic Professional (EMPro®). Al analizar los valores predichos por el modelo teórico (Th. En la figura 5), la simulación electromagnética (Sim. En la figura 5) y los valores experimentales (Exp. en la figura 5), observamos que la SRF y el factor de calidad máximo medidos (1.065GHz y 334.7) se desvían relativamente poco (< 12% y < 10%) de los valores teóricos (0.947 GHz y 338.6) y simulados (1.002 GHz y 302.2). Además, se encontró que el valor experimental tuvo una desviación máxima de 20.3% y 25.9% con respecto a su valor teórico y simulado, respectivamente. Adicionalmente, en una banda de frecuencias amplia (i.e., 0.1 GHz y 0.8 GHz) la desviación siempre es inferior al 20%.
 Figura 5a.
Valores experimentales, simulados y teóricos del Q. a) Q vs. f (GHz).
Figura 5a.
Valores experimentales, simulados y teóricos del Q. a) Q vs. f (GHz).
Fuente: elaboración propia.
 Figura 5b.
Valores experimentales, simulados y teóricos del Q. b) Error absoluto.
Figura 5b.
Valores experimentales, simulados y teóricos del Q. b) Error absoluto.
Fuente: elaboración propia.
Eficiencia y el Factor A del enlace
Para verificar experimentalmente la capacidad de predicción del modelo propuesto, considerando tanto el factor A como la eficiencia energética de un enlace asimétrico basado en PSOI, los factores estimados del caso de estudio fueron comparados con factores simulados y medidos. Los valores teóricos (estimados por el modelo) fueron calculados usando una simulación circuital, basada en inductancias acopladas implementada en el software Advanced Design System (ADS®), los valores de los componentes de la simulación fueron calculados usando el modelo propuesto (implementado en un script de MATLAB®). La simulación electromagnética de onda completa implementada en el software EMPro®, estas implementaciones se ilustran en la figura 6. Experimentalmente se midieron los parámetros de dispersión del caso de estudio, utilizando la configuración experimental que se muestra en la figura 3b. Los condensadores CR1(2) son externos al PSOI, y fueron calculados para que junto con C1(2) (condensadores intrínsecos al PSOI) formaran una capacitancia equivalente que resuene con el inductor L1(2) en cada frecuencia de prueba, además cuatro condensadores de 1pF fueron adicionados para acoplar parcialmente el enlace con la impedancia del puerto del VNA (i. e., 50), lo cual disminuye el error introducido por el VNA en la medida, debido al desacople de impedancias. Específicamente, al medir con acople parcial de impedancias, se garantiza que el valor del coeficiente de reflexión sea cercano a cero, región de operación en la cual el VNA mide la impedancia con un error menor al 10%. Todos los condensadores usados tienen factores de calidad elevados (mayores a 1000) para disminuir el impacto de las perdidas parasitarias en las medidas.
 Figura 6a.
Implementación del modelo del enlace inductivo. a) Modelo circuital ADS®.
Figura 6a.
Implementación del modelo del enlace inductivo. a) Modelo circuital ADS®.
Fuente: elaboración propia.
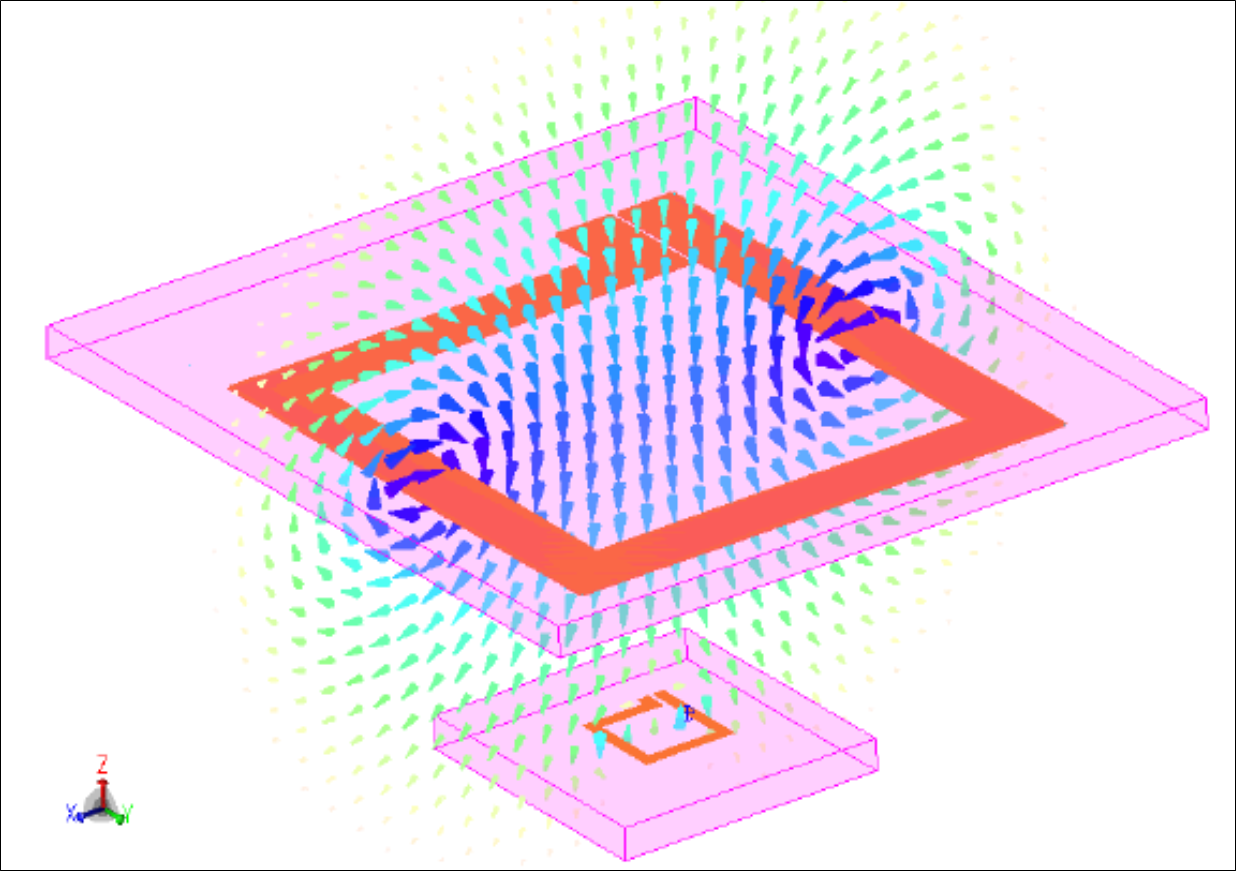 Figura 6b.
Implementación del modelo del enlace inductivo. b) Simulación de onda completa en EMPro®
Figura 6b.
Implementación del modelo del enlace inductivo. b) Simulación de onda completa en EMPro®
Fuente: elaboración propia.
El experimento se realizó en diez frecuencias cercanas a la frecuencia optima de operación del enlace, para conseguir una resolución aceptable cerca del punto máximo del Factor A. A partir de los parámetros de dispersión medidos, se calculó la eficiencia y el factor A usando las siguientes ecuaciones [15]:
donde, sxz es parámetro de dispersión con entrada en el puerto x y salida en el puerto z, y KMAG es la máxima ganancia disponible de la red de dos puertos [20]:
En la figura 7 y en la tabla 2, se comparan los resultados experimentales de la eficiencia y el factor A del enlace asimétrico con sus valores teóricos y simulados. La eficiencia energética y el factor A teóricos fueron calculados a partir de los parámetros de dispersión calculados a partir del modelo propuesto, y las ecuaciones (17) y (18). Al analizar los resultados presentados en la figura 7 y en la tabla 2, los valores predichos por el modelo teórico (Th. en la figura 7) y la simulación electromagnética (Sim. en la figura 7), observamos que son muy similares y que sus diferencias son inferiores al 20% en casi todo el rango de frecuencia. Además, ambas predicciones son consistentes con el resultado experimental (exp. en la figura 7), tanto en su forma y como en la frecuencia óptima esperada, aunque difieren los valores absolutos. Además, la diferencia absoluta entre los valores máximos para la eficiencia y el factor A del enlace (comparando el modelo con las mediciones) es de 28% y 50%, respectivamente. Considerando el modelo y las simulaciones, estas diferencias son de 2% y 5%, respectivamente.
Tabla 2.
Valores máximos factores analizados del enlace inductivo

Fuente: elaboración propia.
 Figura 7a.
Resultados de los factores analizados del enlace inductivo. a) Factor A vs. f (GHz).
Figura 7a.
Resultados de los factores analizados del enlace inductivo. a) Factor A vs. f (GHz).
Fuente: elaboración propia.
 Figura 7b.
Resultados de los factores analizados del enlace inductivo. b) Error porcentual del Factor A.
Figura 7b.
Resultados de los factores analizados del enlace inductivo. b) Error porcentual del Factor A.
Fuente: elaboración propia.
 Figura 7c.
Resultados de los factores analizados del enlace inductivo. c) Eficiencia vs. f (GHz).
Figura 7c.
Resultados de los factores analizados del enlace inductivo. c) Eficiencia vs. f (GHz).
Fuente: elaboración propia.
 Figura 7d.
Resultados de los factores analizados del enlace inductivo. d) Error porcentual de la Eficiencia.
Figura 7d.
Resultados de los factores analizados del enlace inductivo. d) Error porcentual de la Eficiencia.
Fuente: elaboración propia.
Discusión y análisis de resultados
El modelo presentado es consistente con las simulaciones electromagnéticas de onda completa y los resultados experimentales, por lo tanto, puede ser usado para optimizar enlaces inductivos basados en PSOI. A pesar de que el impacto de los elementos parasitarios en la medida fue sistemáticamente minimizado, aparecieron discrepancias significativas entre los datos teóricos y simulados con los datos experimentales. Las técnicas para minimizar estas discrepancias fueron: 1) Conectores U.FL en lugar de conectores SMA. 2) La caracterización del factor de calidad se realizó con una técnica sin contacto. 3) La medición de los parámetros de dispersión se realizó con el VNA en condiciones de acople parcial.
Las discrepancias entre los resultados experimentales y las variables estimadas por la simulación y el modelo teórico, se pueden explicar parcialmente por los desafíos experimentales, que fueron: 1) la interacción entre el inductor bajo prueba y el sistema de medida, especialmente significativo en las frecuencias cercanas a la SRF del inductor; 2) el error en la medición de valores de resistencia muy bajos (1 o menos) a altas frecuencias y valores muy altos (1 k o más) en UHF y VHF utilizando un VNA; 3) la medición de los parámetros de dispersión usando un VNA en condiciones de desacople de impedancias; 4) la presencia de resistencias parasitarias comparables con los valores resistivos de los componentes a medir, estas parasitarias están relacionadas con el factor de calidad de los condensadores, con el proceso de calibración e incluso con la soldadura de los componentes.
Conclusiones
En este artículo, se propuso un modelo de enlaces inductivos asimétricos basado en inductores PSOI, el cual fue validado mediante simulación y experimentalmente. Las predicciones del modelo fueron consistentes con los resultados simulados y experimentales. Como una contribución teórica, en este documento presenta una ecuación analítica para calcular el factor A, a partir de los parámetros de dispersión de la red de dos puertos, lo cual simplifica su medición experimental con un VNA convencional.
Agradecimientos
El primer autor desea agradecer a Colciencias y a la Pontificia Universidad Javeriana por el apoyo financiero. Además, los autores desean agradecer al CNPq y al INCT/NAMITEC por su apoyo financiero parcial, y a todos los estudiantes del Grupo de circuitos integrados de radiofrecuencia de la Universidad Federal de Santa Catarina (GRF/UFSC) por las importantes discusiones.
References
[1] A. Whitmore, A. Agarwal, and L. Xu, “The internet of things, a survey of topics and trends,” Inform. Syst. Frontiers, vol. 17, no. 2, pp. 261–274, 2014.
[2] S. Movassaghi, M. Abolhasan, J. Lipman, D. Smith, and A. Jamalipour, “Wireless body area networks: A survey,” IEEE J. Comm. Surveys & Tutorials, vol. 16, no. 3, pp. 1658–1686, 2014.
[3] A. Fajardo and F. Rangel de Sousa, “A taxonomy for learning, teaching, and assessing wireless body area networks,” in Proc. IEEE 7th Latin American Symp. Circuits Syst. (LASCAS), 2016, pp. 179–182.
[4] M. A. Hannan, S. Mutashar, S. A. Samad, and A. Hussain, “Energy harvesting for the implantable biomedical devices: issues and challenges,” Biomed. Eng. OnLine, vol. 13, no. 1, p. 79, 2014.
[5] A. B. Amar, A. B. Kouki, and H. Cao, “Power approaches for implantable medical devices,” Sensors, vol. 15, no. 11, pp. 28 889–28 914, 2015.
[6] X. Lu, P. Wang, D. Niyato, D. I. Kim, and Z. Han, “Wireless charging technologies: Fundamentals, standards, and network applications,” IEEE J. Comm. Surveys & Tutorials, vol. 18, no. 2, pp. 1413–1452, 2016.
[7] M. Zargham and P. G. Gulak, “Fully integrated on-chip coil in 0.13 um cmos for wireless power transfer through biological media,” IEEE Trans. Biomed. Circuits Syst., vol. 9, no. 2, pp. 259–271, April 2015.
[8] F. L. Cabrera and F. R. de Sousa, “Achieving optimal efficiency in energy transfer to a cmos fully integrated wireless power receiver,” IEEE Trans. Microw. Theory Tech., vol. 64, no. 11, pp. 3703–3713, 2016.
[9] F. L. Cabrera and F. R. de Sousa “Optimal design of energy efficient inductive links for powering implanted devices,” in IEEE Topical Conf. Biomed. Wireless Tech. Netw. Sensing Syst. (BioWireleSS), Jan 2014, pp. 37–39.
[10] A. Fajardo, F. L. Cabrera, and F. R. de Sousa, “Characterization of high-Q inductors up to its self-resonance frequency for wireless power transfer applications,” IEEE Microw. and Wireless Comp. Lett., vol. 28, no. 12, pp. 1071–1073, 2018.
[11] K. O., “Estimation methods for quality factors of inductors fabricated in silicon integrated circuit process technologies,” IEEE J. Solid-State Circuits, vol. 33, no. 8, pp. 1249–1252, Aug 1998.
[12] R. Doldan, A. J. Gines, and A. Rueda, “Inductor characterization in rflc-vcos”, in IEEE 4th Latin Amer. Symp. Circuits Syst (LASCAS)., Feb2013, pp. 1–4.
[13] A. Fajardo, F. R. de Sousa, F. L. Cabrera, V. Brusamarello, and R. Azambuja, “Scalable model of planar square one-turn inductors for wireless power transfer applications,” in 2018 IEEE Wireless Power Transfer Conf. (WPTC), 2018, pp. 1–4.
[14] F. L. Cabrera, “Contributions on the optimization of wireless energy transfer efficiency for miniaturized electronic devices,” Ph.D. dissertation, Federal University of Santa Catarina, 2016.
[15] A. Fajardo, “Contributions on the energy flow modeling in a self-sustainable wireless energy transfer system based on efficient inductive links,” Ph.D. dissertation, Federal University of Santa Catarina, 2018.
[16] S. Arvas, “Spiral inductor model extraction: A survey of the field,” in IEEE Wireless Microwave Tech. Conf. (WAMICON), April 2012, pp.1–7.
[17] S. Li and C. C. Mi, “Wireless power transfer for electric vehicle applications,” IEEE J. Emerging Select. Topics Power Electron., vol. 3, no. 1, pp. 4–17, March 2015.
[18] T. Ohira, “What in the world is Q” IEEE Microwave Mag., vol. 17, no. 6, pp. 42–49, June 2016.
[19] B. Razavi, RF microelectronics, 2nd ed. Prentice Hall New Jersey, 2011.
[20] D. M. Pozar, Microwave Engineering 3e. Wiley, 2006.
Notas
*
Review paper (Artículo de revisión).
Notas de autor
a Autor de correspondencia: fajardoa@javeriana.edu.co
Información adicional
Cómo citar este artículo / How to cite this article: A. Fajardo, F. L. Cabrera, F. Rangel-de-Sousa, “A model of Asymmetric Inductive Links for Power Transfer Applications with Miniaturized Receivers” Ing. Univ. vol. 27, 2023. https://doi.org/10.11144/Javeriana.iued27.mail






 (1)
(1)

 (2)
(2) (3)
(3) (4)
(4)
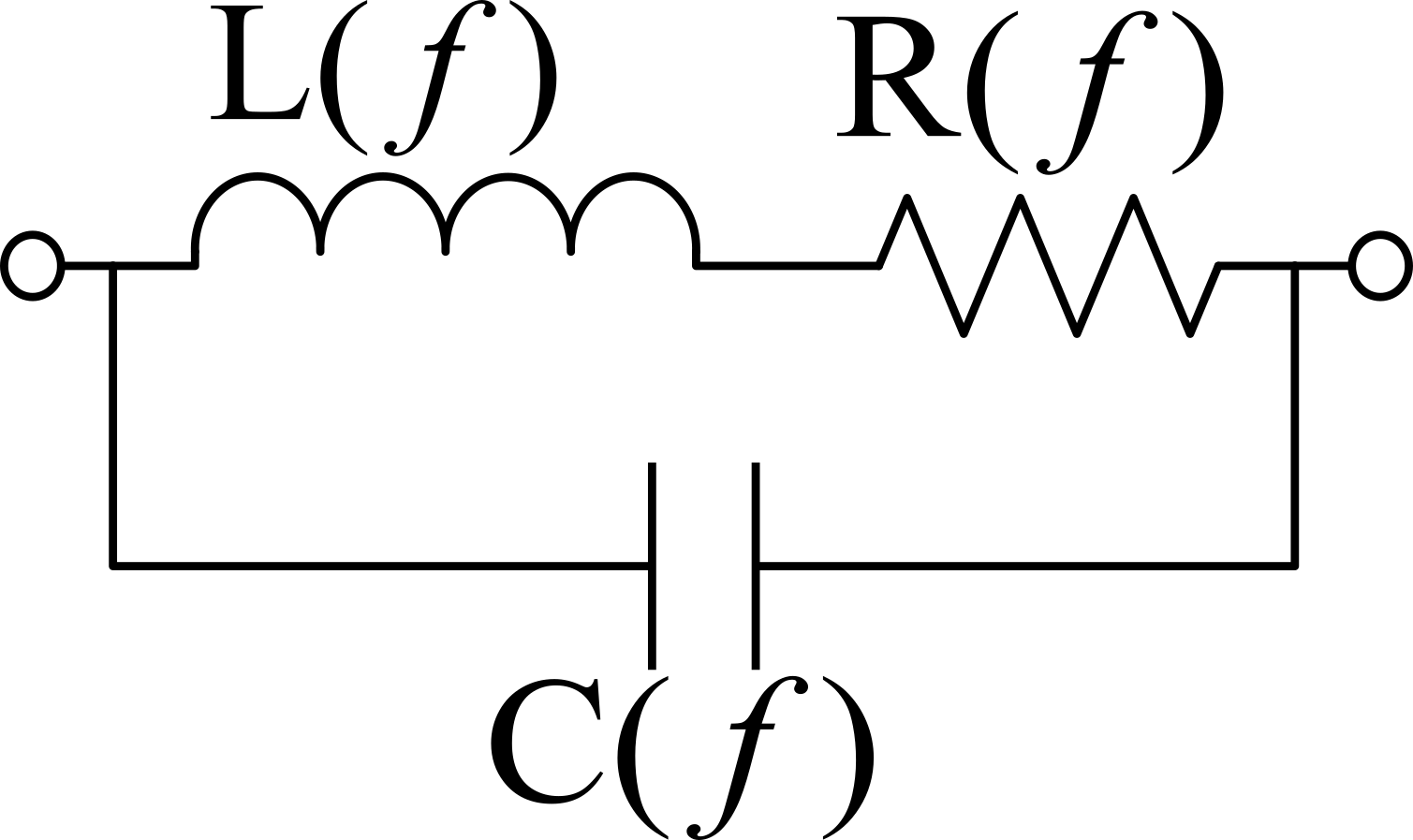
 (5)
(5) (6)
(6) (7)
(7) (8)
(8) (9)
(9) (10)
(10) (11)
(11) (12)
(12) (13)
(13) (14)
(14) (15)
(15) (16)
(16)










 (17)
(17) (18)
(18) (19)
(19)




