Supply Chain Management in the Health Sector
According to the literature [1], the supply chain (SC) integrates suppliers, producers, distributors, and consumers to optimize value creation. Since 2000, the value chain concept has strengthened supply chain management (SCM), thus enhancing control over SC processes [2]. Furthermore, vehicle routing is critical in SCM, as it identifies hidden costs related to transportation, delays, and storage [3]. In this context, SCM also balances supply and demand through constraints on capacity, performance, and stakeholder requirements [4].
In health care, SCM ensures continuous resource availability for effective service delivery. Optimized SCM reduces costs, treatment delays, and inefficiencies, thereby improving patient care quality [5]. Therefore, the present research focuses on designing medical supply pickup-and-delivery routes under travel and service time uncertainty. Hence, the proposed stochastic approach helps assess variability, thus leading to more reliable and risk-aware logistics decisions.
The health care SC must enhance efficiency and sustainability, with cost optimization through logistics improvements. However, health logistics research in Colombia is scarce [6]. Notably, 30% of health care costs in Colombia stem from logistics, with 20–25% linked to surgical product procurement [7].
Effective SCM in health care relies on consistent supply availability [8]. The enhancement of SC resilience requires supplier reliability and timely deliveries. Efficient logistics solutions ensure faster, full deliveries, thereby strengthening health care service continuity [9].
VRP Solution Methods: State-Of-The-Art Methods
The vehicle routing problem (VRP) is a fundamental optimization problem in supply chain management aimed at determining efficient routes for vehicles serving multiple customers [1,2]. Traditional VRP models assume deterministic parameters, such as costs, demand, and travel times. However, real-world logistics often involves uncertainties, thus necessitating stochastic approaches to better capture dynamic operational conditions [10,11]. Two key VRP variants relevant to this study are as follows:
-
- VRP
with time windows (VRPTW): Customers must be served within predefined time
intervals, which is a common constraint in sectors such as perishable goods, medical
logistics, and urban distribution [11].
-
- VRP
with pickup and delivery (VRPPD): In this variant, which is frequently
encountered in e-commerce, ride-sharing, and medical supply chains, goods are
picked up from specific locations and delivered to designated destinations
[12].
Recent studies have explored hybrid models that integrate both time windows and pickup-and-delivery constraints while also incorporating stochastic parameters to model demand variability, travel times, and service durations [13]. VRP solution methods can be categorized into three main types of approaches [14]:
-
- Exact
methods:
Techniques such as branch-and-bound and integer programming provide optimal
solutions but are computationally expensive, which makes them impractical for
large-scale problems [15].
-
- Heuristics: These rule-based algorithms quickly generate
feasible solutions but without guarantees of optimality. Common heuristics
include the savings algorithm and nearest neighbor approach [16].
-
- Metaheuristics: Advanced techniques such as genetic
algorithms (GAs), tabu search (TS), and variable neighborhood search (VNS)
balance solution quality and computational efficiency [17,18].
While exact methods perform well for small-scale problems, heuristics and metaheuristics are widely used in real-world applications, where problem complexity and uncertainty make deterministic approaches impractical [19].
Moreover, when parameters such as travel time, service time, and demand exhibit uncertainty, stochastic optimization techniques become necessary. The two main stochastic approaches identified in the literature are as follows:
-
- Chance-constrained
programming (CCP):
This technique ensures that constraints (e.g., time windows) are met with a
predefined probability threshold (e.g., 95%) [20].
-
- Simheuristics: This approach combines metaheuristics with
simulation techniques (e.g., Monte Carlo) to guide the optimization process
while accounting for uncertainty [4,15].
Simheuristics have gained significant attention because of their ability to integrate probabilistic evaluation into high-quality optimization algorithms, which makes them well suited for complex stochastic VRP problems [21].
Although prior research has explored VRPTW, VRPPD, and stochastic routing individually, an integrated approach that addresses all three components within a unified model remains largely unexplored.
Table 1 summarizes key contributions in the field and categorizes studies on the basis of their treatment of time windows (TWs), service times (STs), travel times (TTs), and pickup-and-delivery (PD) constraints, along with their solution methods (deterministic or stochastic).
A key finding from Table 1 is that while multiple studies have addressed individual stochastic components, few have developed a holistic framework that combines time windows, stochastic travel and service times, and pickup-and-delivery logistics. This research aims to fill this gap by developing a comprehensive optimization model that is applied to a Colombian medical supply company, where stochastic pickup-and-delivery routes must operate under strict time windows and uncertain travel and service times [6,10].
Table 1.
Literature on VRP variants related to the case
study: Time windows (TWs), service time (ST), travel time (TT) and distribution
with pickup and delivery (PD)
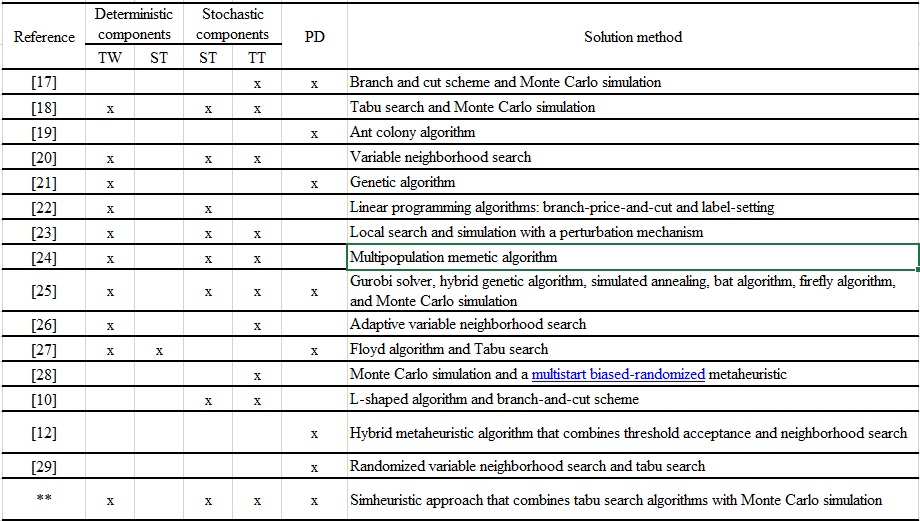
**
Corresponds to the proposed solution
approach
Source: Authors’ own creation.
Materials and Methods
First, a deterministic solution strategy is proposed, wherein travel time uncertainty is not considered. Then, a simheuristic solution is introduced, with due consideration of the stochastic behavior of the parameters in question. Finally, the two methods are compared to select the best method as the proposed strategy for the company. Considering the information technology requirements of the company, the programming language Visual Basic for Applications (VBA) was used to develop the proposed models.
Characterization and Parameterization of the Case Study
The company in which the case study was conducted provides medical supplies in the Colombian health care market by importing, commercializing, and distributing surgery products and equipment. The distribution process includes the delivery and recovery of these items to be returned to their logistics center in Bogotá.
The surgical supplies are transported by three company-owned vehicles that operate in three 8-hour shifts. Each vehicle follows a scheduled route to deliver or pick up items at medical institutions. The company must ensure compliance with hospital time windows, which may change due to surgery schedules. As part of its value promise, it guarantees delivery at least three hours before surgery.
Since the company supplies other cities, some routes include transportation centers, such as bus terminals and airports, where instruments are sent or picked up. The company’s routing scheme is detailed in Figure 1.
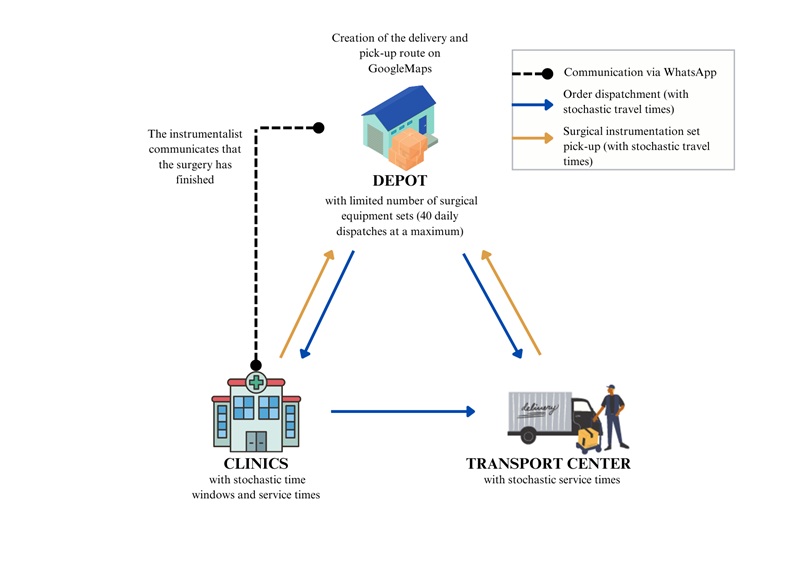 Figure 1.
Distribution route diagram
Figure 1.
Distribution route diagram
Source: Authors’ own creation.
The main problem to be addressed by the present research is that, oftentimes, the company vehicles do not fulfill the time windows set by the health institutions. This implies wasted trips and the impossibility of timely recovery of equipment for its later reutilization and distribution. This situation occurs because the routes are currently designed empirically and without due consideration of travel or service time variability.
A likely solution to this situation is the automation of the route design system, with consideration of travel and service time uncertainty. This is a value-adding strategy for the company since it is likely to facilitate a more efficient and realistic design process that maximizes the fulfillment of the surgery time windows and, hence, the value promise of the company. On these grounds, the purpose of this research is to minimize the OF by considering the total distribution cost and a penalty for time window nonfulfillment.
Deterministic Solution Programming
The deterministic solution is based mainly on the sequential hybridization of two tabu-search-based metaheuristics. According to a literature review in [11], metaheuristics is the most common VRP-solving method. Specifically, tabu search has been consistently found to be a feasible solution for routing problems with time windows and pickup-and-delivery requirements [30].
Figure 2 shows the proposed solution method, which initially operates through the nearest neighbor heuristic (NN). This algorithm enables the development of an initial solution (initSol), which, in turn, constitutes the input of two subsequent tabu search metaheuristics. As shown in Figure 2, the logical order of the algorithm seeks to improve the objective function through the continuous activation of the heuristic and the metaheuristics. The second metaheuristic (TS2) specifically comprises a 100-iteration cycle (z=100) that continuously improves the best solution (bestSol) until the termination criterion is reached.
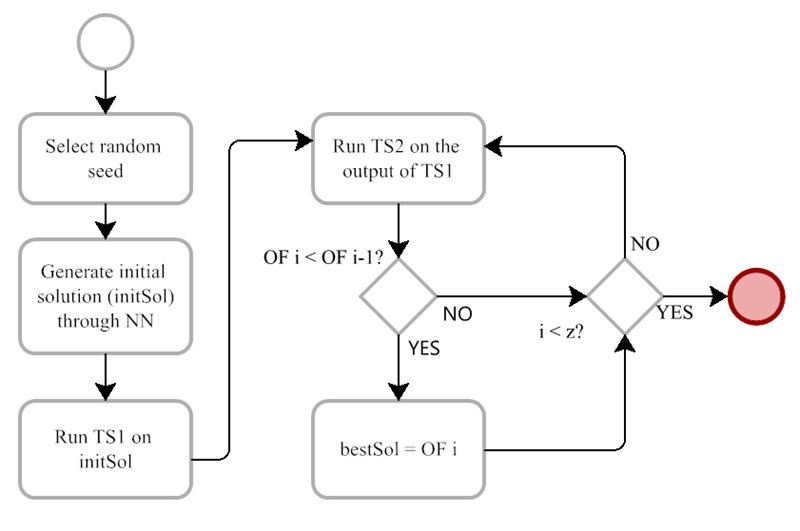 Figure 2.
Deterministic solution programming
Figure 2.
Deterministic solution programming
Source: Authors’ own
creation.
The proposed solution scheme comprises two phases in which tabu search Algorithms 1 (TS1—Figure 3) and 2 (TS2—Figure 4) are executed sequentially. After being fed the solution that results from the NN heuristic (initSol), TS1 operates by applying the following exchange criterion: it initially selects that the node that, not having been previously chosen, is also the closest node to the agreed-upon arrival time (three hours before the surgery). Once the node has been chosen, its assignment to the first position of the route of any of the available vehicles is evaluated by recalculating the corresponding arrival times and OF. If the change leads to a lower OF value, it is accepted, thus defining the best possible route (bestSol). If not, the change is rejected. In either case, if no more than x changes have been tried (x=100), a new node is searched for to restart the cycle. In TS1, the tabu list consists of node reassignments to trucks that have already been evaluated. However, the aspiration criterion allows acceptance of a tabu reassignment if the move leads to an improvement in the objective function. Additionally, as an intensification strategy, in each iteration, the algorithm evaluates the insertion of the selected node into the first position of all routes and selects the alternative that results in the greatest improvement in the objective function.
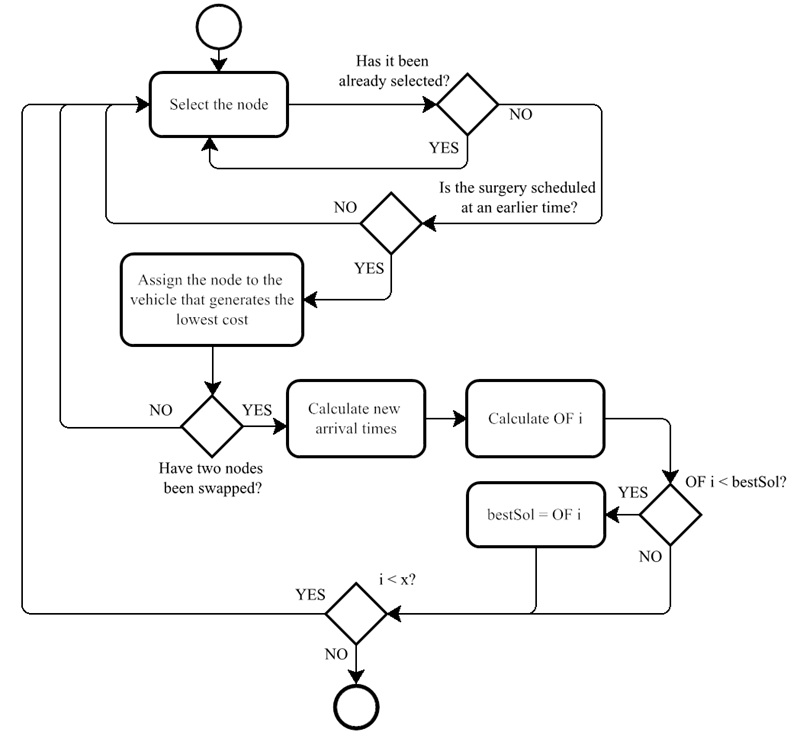 Figure 3.
Tabu Search Algorithm 1 (TS1)
Figure 3.
Tabu Search Algorithm 1 (TS1)
Source: Authors’ own
creation.
TS2 was developed in search of greater savings in the OF. Its input is the best solution generated by TS1. To diversify the exploration in the search space, the exchange criterion of this procedure consists of swapping two random nodes, which do not necessarily have to be on the same route. On the basis of the new route thus created, the arrival times and vehicle loads are updated.
TS2 makes changes without considering vehicle capacity or route duration. Once a route is created, the violation of these constraints is penalized in the calculation of the OF. Similar procedures were applied by [31], [32], [33] and [34], all of which used tabu search, allowed constraint violations, and then penalized the OF.
A penalty is then added to the OF, and if this results in a lower OF value than the existing value, the modification is saved by assigning it as the current best route (bestSol), which allows all nodes to be swapped again. This metaheuristic uses an nxn tabu matrix,where n is the number of nodes at which orders must be picked up or delivered. The matrix ensures that any possible change between nodes is evaluated only once. Hence, once a change is made, it is blocked and is no longer an option for future changes. Consequently, if the evaluated change does not attain a lower OF, it is rejected, and the nodes involved cannot be exchanged again. This algorithm does not implement an aspiration criterion, but the tabu list is reset every time the global objective function improves as an intensification measure. TS2 finishes once all the swaps between nodes (value y) have been evaluated.
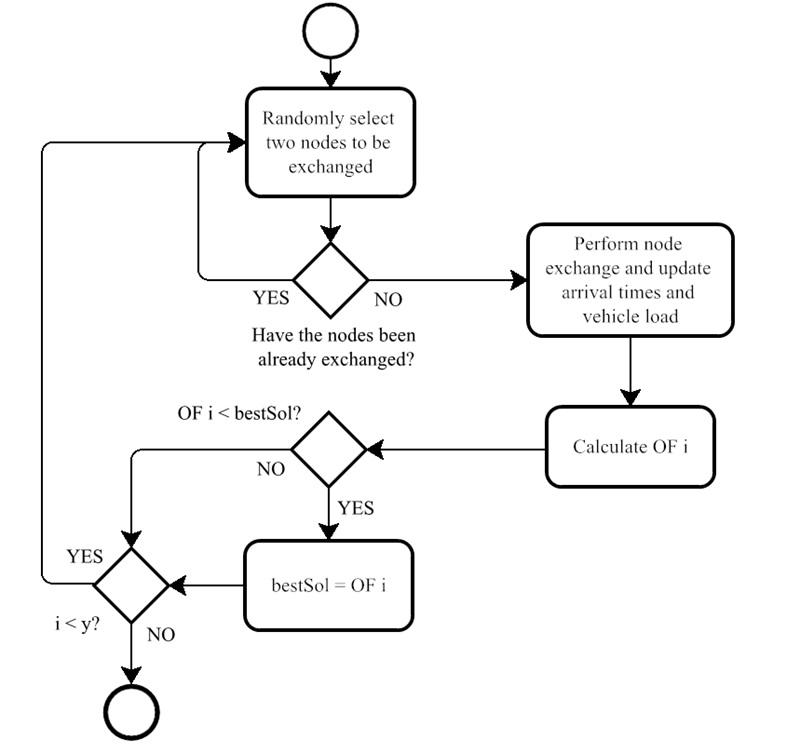 Figure 4.
Tabu Search Algorithm 2 (TS2)
Figure 4.
Tabu Search Algorithm 2 (TS2)
Source: Authors’ own creation.
Stochastic Solution Programming
In this particular case, the simheuristic ( Figure 5 ) starts by calculating the objective function of the route generated by the NN strategy and then evaluates it on w previously generated replicas (the value of w was set at 100 through a validation process), which are generated from an equal number of random iterations of the stochastic parameters (travel time and service time).
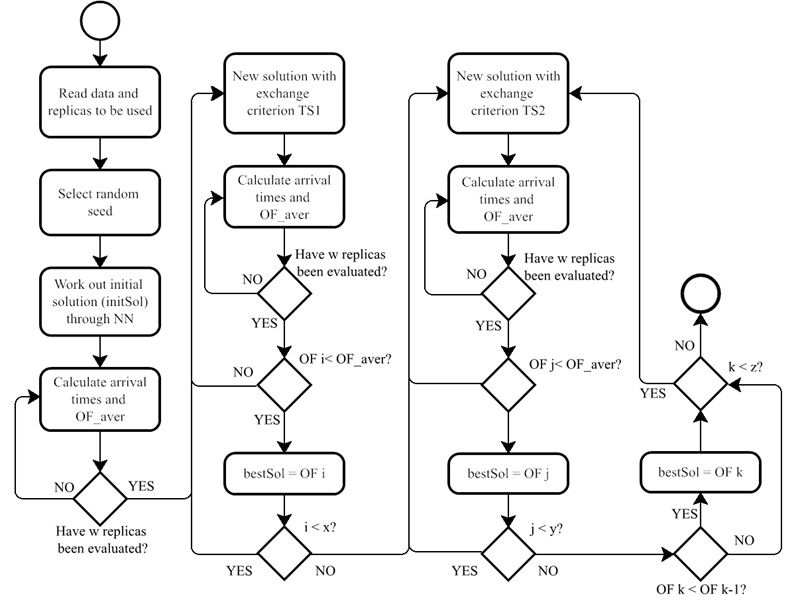 Figure 5.
Stochastic solution programming
Figure 5.
Stochastic solution programming
Source: Authors’ own creation.
After all the replicas have been evaluated, the corresponding average objective function (OF_aver) is calculated and stored. A new solution is subsequently generated by applying the exchange criterion of TS1 (Figure 3) to x changes. As in deterministic programming, x represents the total number of changes made by TS1, which is equal to 100. Every time a change is made by TS1, the solution is evaluated on the w replicas, OF_aver is calculated and saved, and the best solution (bestSol) is updated. A new solution is subsequently generated by applying the exchange criterion of TS2 (Figure 4). For all y exchanges of TS2 (y=100), the solution is evaluated on the w replicas, OF_aver is calculated and saved, and bestSol is updated. Finally, the generation of solutions by TS2 in the simheuristic is executed z times (z=100) to see if it is possible to improve the solution with a better OF_aver value.
Stochastic Service Times
Stochastic service time values were generated via the bootstrap method. This is a particular type of nonparametric Monte Carlo simulation that, to estimate the actual distribution of a population, introduces resampling processes to generate random values from the distribution of an empirical sample [35]. In the current case, node service times were generated by randomly choosing values from the historical data provided by the company. This procedure became necessary because it was not possible to fit the available service-time historical information of each node to any probability distribution.
Stochastic Travel Times
To account for the effect of travel speed variability on the current analysis, the traffic speed was assumed to have a normal probability distribution, in accordance with previous works such as [36], [37] and [38]. This is due to the computational advantage offered by normal distributions in terms of mean and variance determination. In this framework, the travel times were calculated on the basis of the distances between nodes and the estimated traffic speed. The latter was determined from the daily historical records of the city of Bogota.
To establish the value of the variance to be used as a proxy for traffic speed heterogeneity in the present work, four different scenarios were established. [39] discusses three different coefficients of variation for traffic speed, namely, 10%, 17% and 25% of the mean value, which correspond to three different scenarios. In a similar work, [40] implemented variation coefficients of 10%, 20% and 30%. On the basis of the above, the current research assumed a normal traffic speed distribution to influence travel times in four different speed variability scenarios that featured the following variances: 0% deviation (null), 10% deviation (low), 20% deviation (medium) and 30% deviation (high).
Results
Validation of the Route Programming Method
To adequately validate the route scheduling method, two comparisons were made. The first contrasted the deterministic approach with the simheuristic, and the second compared the proposed method to the method used by the company. In the second case, the proposed method corresponded to the best result of the first comparison. In both cases, a simulation was conducted to evaluate the routes through the following indicators:
-
- Objective function (OF): This function
seeks to minimize travel costs between nodes and includes a penalty for not
meeting time window requirements.
-
- Total traveling cost (CT): This variable
corresponds to the total travel cost for visiting all the nodes that need to be
visited.
-
- Percentage of deliveries within
the time window (%CX): This variable relates the number of satisfactory deliveries (i.e., those that took
place at least three hours before the scheduled surgery) to the total number of
deliveries.
These indicators were evaluated in different numbers of instances, depending on the case. In the comparison between the scheduling approaches, 30 instances were assessed. Fifteen of them comprised only 10 nodes each, whereas the other 15 instances covered 15 nodes each. For the comparison between the proposed method and the method used by the company, five instances were used. This relatively small number was because there was no more historical information available from the organization under study. The four different traffic speed variance scenarios were assessed for each of the studied instances. The results of these comparisons are presented below.
Comparison between the Deterministic Approach and the Simheuristic
The comparison analyzed in this section enabled us to evaluate the pertinence of the simheuristic approach to address the effect of the uncertainty in the service times combined with the effects of the different levels of coefficient variation for the traffic speed. Table 2 details the percentages of improvement for the instances, which are classified into two groups, namely, 10-node and 15-node instances, with different variation coefficients (0%, 10%, 20%, and 30%). Furthermore, Table 3 consolidates these results by summarizing the proportion of instances where the simheuristic performed better and presenting the average improvements in the OF, CT, and %CX, as well as the computational time required for the simheuristic approach.
Table 2.
Results obtained for each of the generated
instances
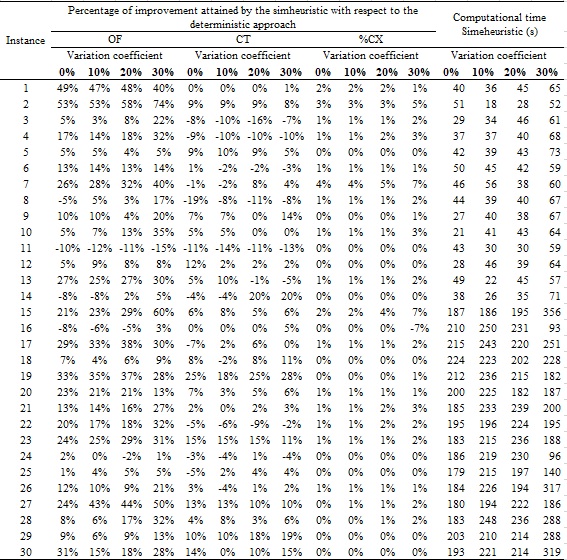
Source: Authors’ own
creation.
Table 3 .
Summary of the obtained results
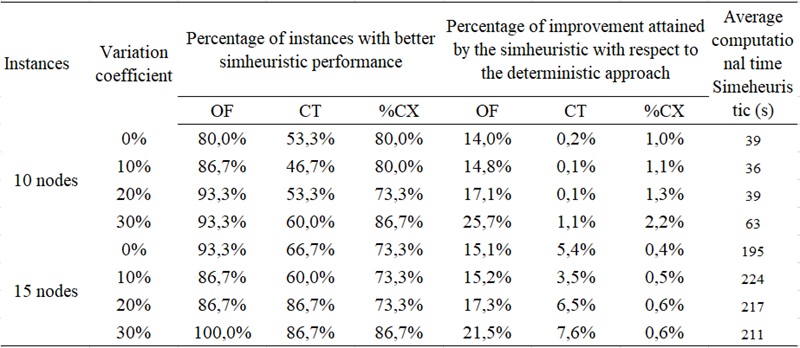
Source: Authors’ own creation.
Overall, as the variation coefficient increased, the simheuristic approach consistently outperformed the deterministic method, especially in larger instances where uncertainty had a greater impact on delivery schedules. For 10-node instances, the percentage of cases with better objective function (OF) values increased from 80.0% at 0% variation to 93.3% at 30%, whereas for 15-node instances, it reached 100% at the highest variation level, which showed that under high uncertainty, the deterministic method was no longer competitive. The improvement in OF was driven largely by penalties for failing to satisfy the time windows, as longer delays significantly disrupt surgery schedules at clinics. Even though most deliveries occurred on time, the magnitude of lateness beyond the surgery schedule strongly affected the OF, which reinforces the need for precise delivery planning.
The total traveling cost (CT) improvements were minimal in the 10-node instances but increased significantly in the 15-node instances, from 5.4% at 0% variation to 7.6% at 30% variation. This indicates that as problem complexity increases, the simheuristic becomes more effective in managing travel efficiency under uncertainty. The percentage of timely deliveries (%CX) remained stable across all variations, thus ensuring that the optimized routes did not compromise the delivery feasibility. However, penalties for exceeding surgery times significantly impacted the OF, which highlights the importance of not only achieving timely deliveries but also minimizing delays.
The computation time increased with the instance size and variation coefficient and ranged from 36–63 seconds for the 10-node instances and from 195–224 seconds for the 15-node instances. In conclusion, as uncertainty increased, the simheuristic approach became even more advantageous, particularly in the 15-node instances, where deterministic methods struggled with variability. Its scalability and robustness make it a highly effective tool for optimizing delivery routes under uncertain conditions, especially in medical logistics, where delays directly affect hospital operations and patient care.
Comparison between the Proposed Method and the Method used by the Company
To evaluate the feasibility of the selected solution approach (simheuristic), it was compared with the current procedure of the company. For this purpose, an evaluation was carried out on five real instances for which the routes established by the company were known to compare them to the routes obtained by means of the simheuristic. As shown in Table 4, the proposed simheuristic approach outperformed the company´s method in terms of the distribution routes generated for the tested instances. Furthermore, in terms of the objective function (OF), the simheuristic outperformed the company’s procedure in at least 40% of the cases and reached its highest success rate (80%) at 20% variation. The improvement in OF remained stable at approximately 33%, which indicates consistent optimization of the objective function across different uncertainty levels.
Table 4.
Comparison between the proposed method (simheuristic)
and the company’s procedure
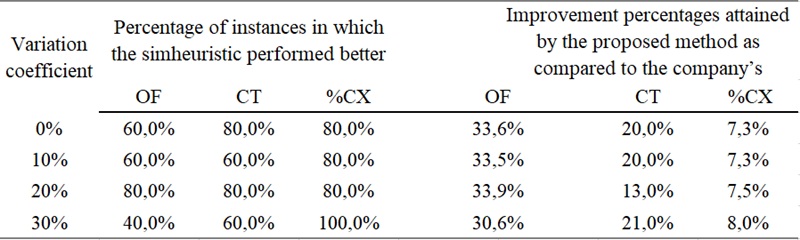
Source: Authors’ own creation.
In terms of CT (traveling cost), the simheuristic achieved its highest performance at 0% and 20% variation (80%), whereas at 10% and 30% variation, the success rate decreased to 60%. The improvement in CT varied, with the highest gain of 21% at 30% uncertainty, which suggests that the method is particularly effective in reducing costs under higher uncertainty.
With respect to %CX (customer satisfaction), the proposed method consistently outperformed the company’s procedure, with a 100% success rate at 30% uncertainty. The improvement percentage in %CX gradually increased from 7.3% (0% and 10%) to 8.0% (30%), which highlights the ability of simheuristics to enhance service quality as uncertainty increases.
Overall, the results demonstrate that the simheuristic method provides significant improvements over the company's current approach, particularly in optimizing OF and CT under uncertain conditions. The consistent gains in %CX further indicate that it is a reliable method for maintaining high customer satisfaction levels.
Conclusions
In this research, the VRP was employed to develop a route scheduling method for the distribution of surgical supplies by a company located in the city of Bogota. Time windows and travel and service times with stochastic behavior were considered in the route planning process. Validation was carried out by comparing the deterministic approach to the stochastic approach and the company’s procedure.
In most cases, the developed simheuristic attained better results than did the deterministic approach for all the traffic speed variation coefficients. Moreover, as the variability increased, the simheuristic method outperformed the deterministic method.
Additionally, the routes generated via the simheuristic were compared with the historical distribution routes of the company. The simheuristic performed better in terms of both OF and %CX: average improvements of 7.5% and 33% were attained in the percentage of timely deliveries (i.e., those fulfilling the company’s value promise) and total cost, respectively.
Considering the current methodology and results, possible future research directions include the use of other search operators for the tabu search approach and other metaheuristics. Furthermore, other ways to obtain stochastic travel times could also be considered with the purpose of obtaining a more realistic representation of the related uncertainty. We also propose gathering more information on service times in a stable scenario after the SARS-CoV-2 health contingency, which had to be addressed in the current research. Similarly, overcoming important limitations of this work, such as the small number of instances that were available for evaluating the difference between the simheuristic and the procedure of the company, would be useful.
Acknowledgments
The authors would like to thank Promed Quirúrgicos for their
information and the opportunity they offered to validate the proposed method.
References
[1] H. B. Díaz Gómez, R. G. García Cáceres, and N. Porcell Mancilla, “Las Pymes: costos en La cadena de abastecimiento,” 2008.
[2] C. A. Díaz, Gestión de la Cadena de Abastecimiento, Primera ed. Bogotá: Fondo editorial Areandino, 2017.
[3] A. Olvera, “Heurísticas para problemas de ruteo de vehículos,” 2004, Montevideo.
[4] A. A. Juan, S. E. Grasman, J. Caceres-Cruz, and T. Bektaş, “A simheuristic algorithm for the Single-Period Stochastic Inventory-Routing Problem with stock-outs,” Simul Model Pract Theory, vol. 46, pp. 40–52, 2014, doi: 10.1016/j.simpat.2013.11.008.
[5] M. Wiger, “Logistic management operationalised in a healthcare context - Understanding care chain effectiveness through logistic theories and systems theory,” 2018.
[6] N. Velasco, J. P. Moreno, and C. Rebolledo, “Logistics practices in healthcare organizations in Bogota,” Emerald Publishing Limited, 2018, doi: 10.1108/ARLA-08-2016-0219.
[7] V. Jonas, F. Andreas, S. Jan, and B. Jens O., “Material logistics in hospitals: A literature review,” Omega (Westport), vol. 69, pp. 82–101, 2017, doi: https://doi.org/10.1016/j.omega.2016.08.004.
[8] B. Godfred, G. Adam, S. Melissa, P. Donkor, M. Charles, and S. Barclay, “Assessment of local supply chains and stock management practices for trauma care resources in Ghana: a comparative small sample cross-sectional study,” BMC Health Serv Res, vol. 23, no. 1, pp. 1–12, 2021, doi: https://doi.org/10.1186/s12913-021-06063-6.
[9] R. Zhong, X. Xu, and L. Wang, “Food supply chain management: systems, implementations, and future research,” Industrial Management and Data Systems, vol. 117, no. 9, pp. 2085–2114, 2017, doi: 10.1108/IMDS-09-2016-0391.
[10] H. H. Doulabi, G. Pesant, and L.-M. Rousseau, “Vehicle routing problems with synchronized visits and stochastic travel and service times: Applications in healthcare,” Transportation Science, vol. 54, no. 4, pp. 1053–1072, 2020, doi: 10.1287/TRSC.2019.0956.
[11] K. Braekers, K. Ramaekers, and I. Van Nieuwenhuyse, “The vehicle routing problem: State of the art classification and review,” Comput Ind Eng, vol. 99, pp. 300–313, 2016, doi: 10.1016/j.cie.2015.12.007.
[12] T. Leelertkij, P. Parthanadee, and J. Buddhakulsomsiri, “Vehicle Routing Problem with Transshipment: Mathematical Model and Algorithm,” J Adv Transp, vol. 2021, p. 15, 2021, doi: 10.1155/2021/8886572.
[13] M. Nasri, A. Metrane, I. Hafidi, and A. Jamali, “A robust approach for solving a vehicle routing problem with time windows with uncertain service and travel times,” vol. 11, pp. 1–16, 2019, doi: 10.5267/j.ijiec.2019.7.002.
[14] N. Labadie, C. Prins, and C. Prodhon, “Metaheuristics for Vehicle Routing Problems,” 2016. doi: https://doi.org/10.1007/978-3-319-45403-0_15.
[15] D. Guimarans et al.,
“A simheuristic approach for the two-dimensional
vehicle routing problem with stochastic travel times,” Simul Model Pract Theory, vol. 89, pp. 1–14, 2018, doi:
https://doi.org/10.1016/j.simpat.2018.09.004.
[16] B. S. Onggo, J. Panadero, C. G. Corlu, and A. A. Juan, “Agri-food supply chains with stochastic demands: A multi-period inventory routing problem with perishable products,” Simul Model Pract Theory, vol. 97, 2019, doi: 10.1016/j.simpat.2019.101970.
[17] A. S. Kenyon and D. P. Morton, “Stochastic vehicle routing with random travel times,” Transportation Science, vol. 37, no. 1, pp. 69–82, 2003.
[18] X. Li, P. Tian, and S. C. H. Leung, “NIO,” Intern. Journal of Production Economics, vol. 125, no. 1, pp. 137–145, 2010, doi: https://doi.org/10.1016/j.ijpe.2010.01.013.
[19] B. Çatay, “A new saving-based ant algorithm for the Vehicle Routing Problem with Simultaneous Pickup and Delivery,” Expert Syst Appl, vol. 37, no. 10, pp. 6809–6817, 2010, doi: https://doi.org/10.1016/j.eswa.2010.03.045.
[20] H. Lei, G. Laporte, and B. Guo, “A generalized variable neighborhood search heuristic for the capacitated vehicle routing problem with stochastic service times,” Sociedad de Estadística e Investigación Operativa, vol. 20, pp. 99–118, 2012, doi: https://doi.org/10.1007/s11750-011-0188-6.
[21] S. Yanik, B. Bozkaya, and R. DeKervenoael, “A new VRPPD model and a hybrid heuristic solution approach for e-tailing,” Eur J Oper Res, vol. 236, no. 3, pp. 879–890, 2014, doi: https://doi.org/10.1016/j.ejor.2013.05.023.
[22] F. Errico, G. Desaulniers, M. Gendreau, W. Rei, and L. Rousseau, “A priori optimization with recourse for the vehicle routing problem with hard time windows and stochastic service times,” Eur J Oper Res, vol. 249, no. 1, pp. 55–56, 2016, doi: https://doi.org/10.1016/j.ejor.2015.07.027.
[23] D. M. Miranda and S. V. Conceição, “The vehicle routing problem with hard time windows and stochastic travel and service time,” Expert Syst Appl, vol. 64, pp. 104–116, 2016, doi: https://doi.org/10.1016/j.eswa.2016.07.022.
[24] A. Gutierrez, L. Dieulle, N. Labadie, and N. Velasco, “A multi-population algorithm to solve the VRP with stochastic service and travel times,” Comput Ind Eng, vol. 125, pp. 144–156, 2018, doi: 10.1016/j.cie.2018.07.042.
[25] Y. Shi, T. Boudouh, O. Grunder, and D. Wang, “Modeling and solving simultaneous delivery and pick-up problem with stochastic travel and service times in home health care,” Expert Syst Appl, vol. 102, pp. 218–233, 2018, doi: 10.1016/j.eswa.2018.02.025.
[26] C. Hu, J. Lu, X. Liu, and G. Zhang, “Robust vehicle routing problem with hard time windows under demand and travel time uncertainty,” Comput Oper Res, vol. 94, pp. 139–153, 2018, doi: 10.1016/j.cor.2018.02.006.
[27] Y. Ma, Z. Li, F. Yan, and C. Feng, “A hybrid priority-based genetic algorithm for simultaneous pickup and decision-makers,” Soft comput, vol. 23, no. 15, pp. 6697–6714, 2019, doi: https://doi.org/10.1007/s00500-019-03754-5.
[28] L. Reyes-Rubiano, D. Ferone, A. A. Juan, and J. Faulin, “A simheuristic for routing electric vehicles with limited driving ranges and stochastic travel times,” SORT, vol. 43, no. 1, pp. 3–24, 2019, doi: 10.2436/20.8080.02.77.
[29] H. B. Ban and P. K. Nguyen, “A hybrid metaheuristic for solving asymmetric distance-constrained vehicle routing problem,” Comput Soc Netw, vol. 8, no. 1, pp. 1–19, 2021, doi: 10.1186/s40649-020-00084-7.
[30] R. Elshaer and H. Awad, “A taxonomic review of metaheuristic algorithms for solving the vehicle routing problem and its variants.,” Comput Ind Eng, vol. 140, p. 106242, 2020, doi: https://doi.org/10.1016/j.cie.2019.106242.
[31] O. Bräysy and M. Gendreau, “Vehicle routing problem with time windows, Part II: Metaheuristics,” Transportation Science, vol. 39, no. 1, pp. 119–139, 2005, doi: https://doi.org/10.1287/trsc.1030.0057.
[32] J. Brandão, “Metaheuristic for the Vehicle Routing Problem with Time Windows,” Meta-Heuristics, pp. 19–36, 1999, doi: https://doi.org/10.1007/978-1-4615-5775-3_2.
[33] J.-F. Cordeau, G. Laporte, and A. Mercier, “A unified tabu search heuristic for vehicle routing problems with time windows,” Journal of the Operational Research Society, vol. 52, pp. 928–936, 2001.
[34] H. Chuin-Lau, M. Sim, and K. Meng-Teo, “Vehicle routing problem with time windows and a limited number of vehicles,” Eur J Oper Res, vol. 148, no. 3, pp. 559–569, 2003, doi: https://doi.org/10.1016/S0377-2217(02)00363-6.
[35] S. N. Gil-Abreu, “Bootstrap en poblaciones finitas,” 2014.
[36] M. A. Figliozzi, “The impacts of congestion on commercial vehicle tour characteristics and costs,” Transp Res E Logist Transp Rev, vol. 46, no. 4, pp. 496–506, 2010, doi: https://doi.org/10.1016/j.tre.2009.04.005.
[37] A. R. Güner, A. Murat, and R. B. Chinnam, “Dynamic routing under recurrent and non-recurrent congestion using real-time ITS information,” Comput Oper Res, vol. 39, no. 2, pp. 358–373, 2012, doi: https://doi.org/10.1016/j.cor.2011.04.012.
[38] G. Kim, “Travel time estimation in vehicle routing problem,” IEEE International Conference on Industrial Engineering and Engineering Management, pp. 1004–1008, 2017.
[39] Y. Hollander, “Direct versus indirect models for the effects of unreliability,” Transp Res Part A Policy Pract, vol. 40, no. 9, pp. 699–711, 2006, doi: https://doi.org/10.1016/j.tra.2005.12.007.
[40] Y. Hollander and R. Liu, “Estimation of the distribution of travel times by repeated simulation,” Transp Res Part C Emerg Technol, vol. 16, no. 2, pp. 212–231, 2008, doi: https://doi.org/10.1016/j.trc.2007.07.005.
Notes
Conflicts of
interest
The authors have no conflicts of
interest to declare.
*
Research article
Author notes
aCorresponding author. E-mail: bejarano.carlos@javeriana.edu.co
Additional information
How to cite this article: W. Guevara, C. del C. Mena, L. Pérez, C. Montoya, M.
Caro, C. Bejarano, S. Bolívar, C. Delgado, “An algorithm for the Stochastic Delivery-And-Pickup Vehicle
Routing Problem with Time Windows as applied to Surgical Medical Supplies” Ing. Univ. vol. 29, 2025. https://doi.org/10.11144/Javeriana.iued29.asdp