Introduction
Students face difficulties in developing geometric thinking and its relationship to the analytical approach, both in elementary (basic) and secondary education ([1]; [2] and [3]), and at the university level. This aspect is fundamental for the interpretation of graphic models applied to engineering situations, such as the geometric design of Simple Circular Curves (SCCs). The incorporation of information and communication technologies (ICTs) in the classroom emerges as an alternative to improve geometric and analytical thinking ([4]).
ICTs are innovative tools that stimulate students’ interest, curiosity, creativity, and analytical skills to solve problems from different perspectives ([5] and [6]). Several authors advocate the incorporation of ICTs to improve the teaching-learning process ([7], [8], and [9]). For example, the use of GeoGebra favors the learning process of two- and three-dimensional representations [10]. Therefore, a curricular proposal was proposed, integrating the use of GeoGebra, a free software, based on Stenhouse’s curricular principles [11], where the teacher assumes the role of researcher in the classroom.
A teacher-researcher in a class on Road Surveying identified students’ difficulties related to the mathematical and geometric modeling of planimetric elements in the geometric design of roads. They showed difficulties in identifying the orientation of a Delta deflection angle (Δ), calculating the abscissas and coordinates of the Beginning of the Curve (BC) and Beginning of Tangent (BT) points, as well as the graphical resolution of the SCCs. These difficulties motivated the need to strengthen learning in this area.
To address this problem, the following research question was posed: How can digital technology contribute to the teaching-learning process of the elements of an SCC for a road? The hypothesis stated that the development of a GeoGebra Applet for SCCs would contribute to the teaching-learning of the calculation, interpretation, and representation of the horizontal geometric design of a road. In this context, the purpose of the research was to develop a teaching-learning proposal that would strengthen the geometric and mathematical aspects of the planimetric elements of an SCC using an Applet programmed in GeoGebra. This software allows the output to be graphically visualized and georeferenced in a planar coordinate system, facilitating the calculation of geometric elements and allowing students to interact with the model in real time. This demonstrates the implications of the spatial analysis required in the practice of topography (land surveying).
Materials and Methods
A mixed methodology was proposed, integrating qualitative and quantitative methods in the study. These methods complement each other, allowing for both statistical analysis and analysis of the responses to open-ended questions, which reflect the subjective perspective of each individual [12]. Hypothesis testing was carried out in four stages (Figure 1).
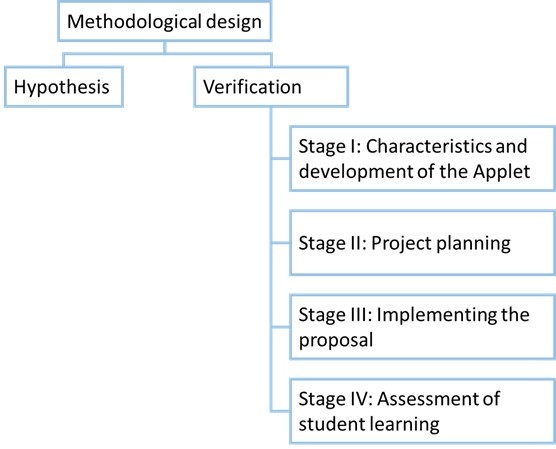 Figure 1.
Methodological Design of the Research
Figure 1.
Methodological Design of the Research
Source: Author.
In the first stage, we identified the characteristics of the ICT resources for the development of geometric modeling of a CCS. This process included the conceptualization of topics, definitions of the CCS design, and a review of the regulations in force at the time of the proposal’s implementation [13]. This multidisciplinary work between surveying technologists, engineering students, and professors successfully established links between the disciplinary and educational aspects.
Two applets were programmed. The first, called “Principles of Planimetry Applied to Roads,” presents an interface that displays a three-point diagram (A, B, and C) that generates an alignment. The user must enter the coordinates of these points in the input fields, and the resulting alignment configuration is displayed in the graphical view. The applet includes check boxes that allow you to show or hide information about the northing and easting projections between each pair of points, the azimuth, the delta, and the alignment, as shown in Figure 2.
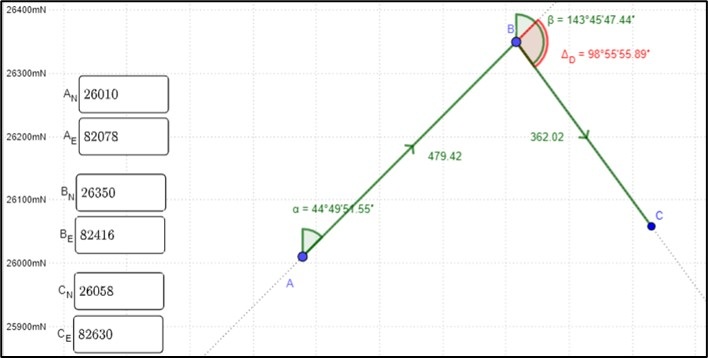 Figure 2.
Applet of Planimetry Applied to Roads
Figure 2.
Applet of Planimetry Applied to Roads
Source: Author.
The second applet, called “Simple Circular Curve,” offers the user the ability to interact with and adjust the curve’s elements, automatically calculating geometric components such as the tangent (T), the external curve (E), the curve length using the arc method (L), and the long chord (LC). It also displays the abscissas of the curve point (CP) and the tangent point (TP) with their respective coordinates, reflecting changes in real time.
The integration of these Applets into teaching facilitates the graphical representation of the curve and its spatial location and encourages the analysis of Simple Circular Curves (SCC) exercises, contributing to the student learning process.
The Applet requires the azimuth, the curve deflection angle, the opening direction, and the curve radius as input data, as well as the north and east coordinates of the alignment’s Point of Intersection (PI) and the abscissa assigned by the exercise to the curve’s starting point. Once these data are entered, the Applet automatically calculates, in meters, several geometric elements of the CCS, including the curve tangent, the curve length (arc method), the long chord, the external chord, and the middle ordinate.
In addition, it records the coordinates of the PC and PT points and calculates the abscissas of the PI and PT points. Finally, the Applet displays a graphical representation of the curve in top view, including its geometric elements and their spatial distribution, as shown in Figure 3. In summary, the Applet consists of three parts: data entry (P1 in green), the presentation of numerical results (P2 in red), and the curve visualization (P3 in blue). Its functionality was verified by solving topography and road exercises and problems ([14] and [15]).
The second stage aimed to support teachers and students in promoting their understanding of the elements of a CCS on the road.
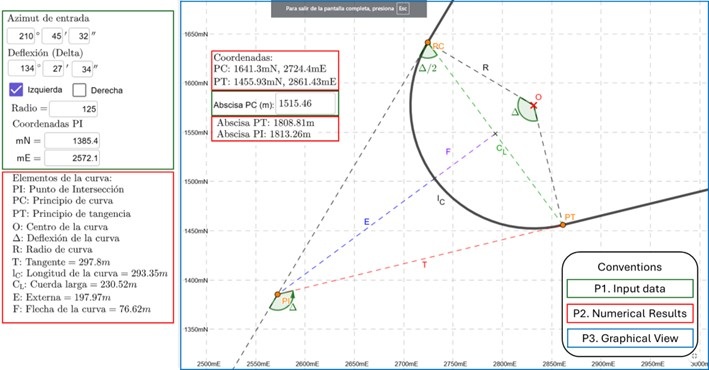 Figure 3:
Parts of
the Simple Circular Curve Applet
Figure 3:
Parts of
the Simple Circular Curve Applet
Source: Author.
The classroom project planning consisted of three parts, as shown in Figure 1: a) administering the pretest, b) teaching how the Applet works, and c) reinforcing student learning.
For this proposal, a teaching sequence was chosen, understood as a set of activities planned in an organized and coherent manner, developed in a specific order to achieve specific learning outcomes. This sequence is designed to promote progression in the teaching-learning process, adapt to student needs, facilitate assessment and feedback, and ensure alignment with established educational objectives. In addition, GeoGebra Classroom was used to complement the process. The three parts of the second stage are described below.
Part a: Conducting a Pretest
In a previous class, students were asked to complete a pretest using a calculator, pencil, and paper. In the hypothetical exercise, students were asked to calculate three circular curves, using five points with their respective northing, easting, and radius as input data (Table 1).
Table 1:
Input Data for the Hypothetical Exercise
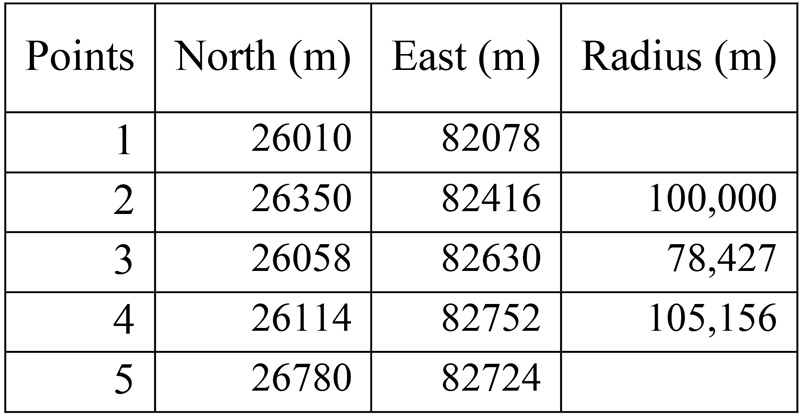
Source: Author.
In the exercise, students were required to calculate and obtain: the elements of the circular curves (T, L, and LC), as well as determine the abscissas and coordinates of the points PC and PT. The pretest assessment criteria were established by the instructor teaching the Road Surveying I course; therefore, no assessment rubrics were used.
Part b: Teaching the Applet’s Function
After the pretest class, the teaching assistants explained how the Principles of Planimetry Applied to Roads and Simple Circular Curves Applets function.
Part c: Reinforcing Student Learning
The purpose of this part was for students to interact with the Applets, entering input data to obtain the azimuths and then the two additional CCSs.
The third stage consisted of implementing the proposal in the classroom during the second semester of 2023, as a complement to the study of horizontal geometric road design. The session was held in a computer lab with sixteen students. After an initial evaluation, the teaching assistants corrected part of the exercise using the Applets and explained how they worked in class. The students followed the instructions and interacted with the Applets to obtain the data and a graphical representation of the first curve.
Given that the initial assessment did not include entry azimuths or deltas, but only a list of planar coordinates, the “Principles of Planimetry Applied to Roads” applet (https://www.geogebra.org/m/gfpptaty) was used. Students were instructed to enter the coordinates of the first curve in the corresponding fields: AN and AE for the first point, BN and BE for the Point of Intersection (POI) coordinates, and CN and CE for the POI of the next curve. They were then able to view the distances, azimuths, and delta formed by the points.
Since the activity required students to interact with the applets, they were asked to enter the entry azimuth, delta, direction, initial radius, and POI coordinates in the “Simple Circular Curve” applet (https://www.geogebra.org/m/skmdwc4j). In addition, the abscissa of the Curve Point (CP) was manually calculated and then entered into the corresponding field. This process yielded the design of Curve 1, as illustrated in Figure 4.
Once the instructions on how the Applet works were completed, the third stage began. After calculating the spatial and geometric elements of the first CCS, the students were asked to repeat the same procedure for the other two curves from the pretest. They were then asked to capture screenshots of the results obtained in the Applet for each curve and attach them to a Word file containing all three screenshots. This file was uploaded to an available space in the GeoGebra Classroom.
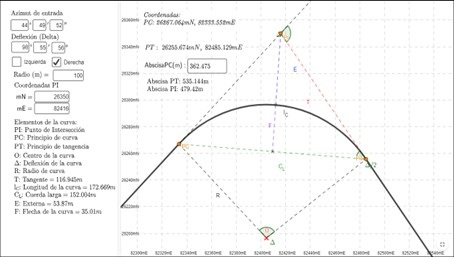 Figure 4:
Solution to Curve 1
Figure 4:
Solution to Curve 1
Source: Author.
In the fourth stage, the students’ learning was assessed. To understand their perceptions of the use of the Applet in the learning process, four sections of open-ended questions were posed, focusing on: 1) The effects of the change in direction in the Delta on the coordinates of PI, PT, and CP. 2) The variation in the geometric elements of the curve with changing radius. 3) The contribution of the Applet to identifying the geometric elements of the curve. 4) The impact of interaction with the Applet on learning.
Results
Data analysis was conducted quantitatively, by analyzing the pretest responses, and qualitatively, by analyzing the answers to the open-ended questions posed in sections C and D of the Simple Circular Curve activity in the GeoGebra Classroom.
a. Quantitative Analysis
The answers provided by the students in the pretest were analyzed using a spreadsheet, considering three criteria: a) the elements of the curve, b) the coordinates of the main points, and c) the abscissas of the main points. The correct answers to the pretest using the “Simple Circular Curve” Applet are presented in Table 2.
Table 2:
Correct Pretest Answers Obtained Using the GeoGebra Applet
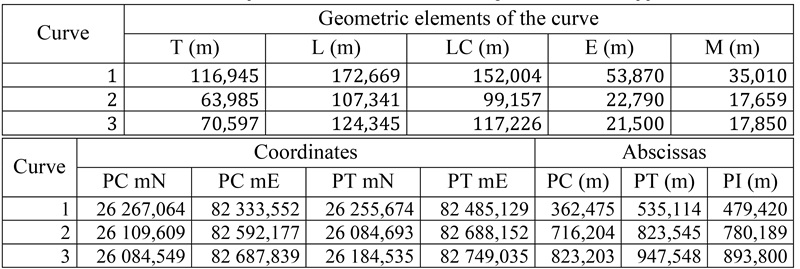
Source: Author.
In the first criterion, the geometric elements of the CCS were analyzed: the tangent (T), curve length (L), long chord (LC), external chord (E), and Middle ordinate (M) of the CCS. Students had difficulties in the pretest when calculating these elements on the three curves, the most common error being the incorrect determination of the delta, which led to inaccurate element calculations. However, by using the applets, students were able to successfully interact and determine the elements of the evaluated curves, including the delta.
Figure 5 shows the number of correct student answers in the pretest and when using the “Simple Circular Curve” applet to calculate the geometric elements.
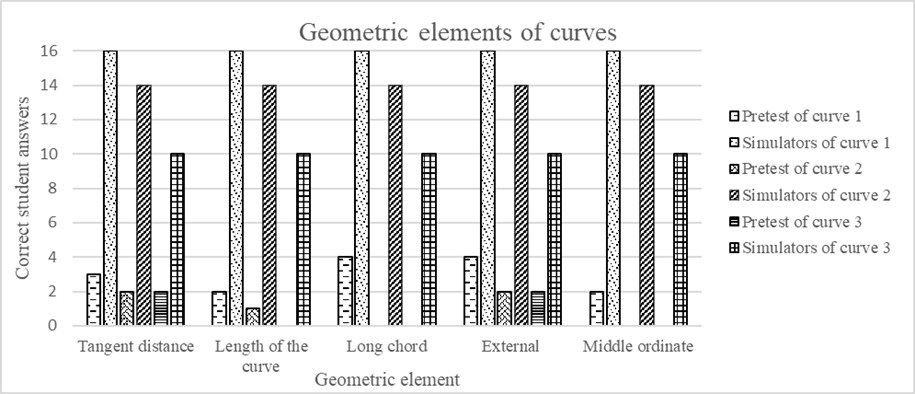 Figure
5:
Number of Correct Student Answers in the Pretest and
Using the Simulators for the Geometric Elements of Circular Curves
Figure
5:
Number of Correct Student Answers in the Pretest and
Using the Simulators for the Geometric Elements of Circular Curves
Source: Author.
The second criterion evaluated the coordinates of the main points of the circular curve, the Point of Tangency (PT) and the Curve Point (CP), given that the Point of Intersection (PI) was provided in the exercise statement. During the pretest, students had difficulty calculating these coordinates due to the lack of entry and exit azimuths for the circular curves. However, when interacting with the Applets, a greater number of students were able to determine the coordinates of the main points of the three curves, as seen in Figure 6.
Finally, the third criterion evaluated the calculation of the PC and PT abscissas. In general, students experienced difficulties performing these calculations manually, using a pencil, calculator, and paper, both in the pretest and when using the Applets.
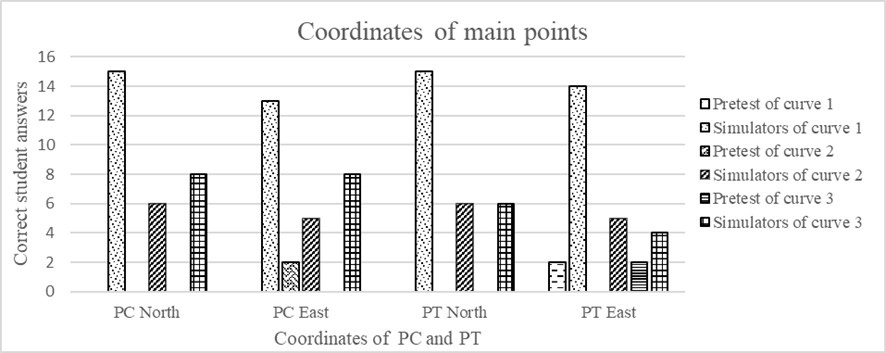 Figure
6:
Summary of Correct Answers for the Coordinate
Criterion at the Main Points of the CCS
Figure
6:
Summary of Correct Answers for the Coordinate
Criterion at the Main Points of the CCS
Source: Author.
Figure 7 summarizes the
students’ correct answers for calculating the abscissas of the three curves.
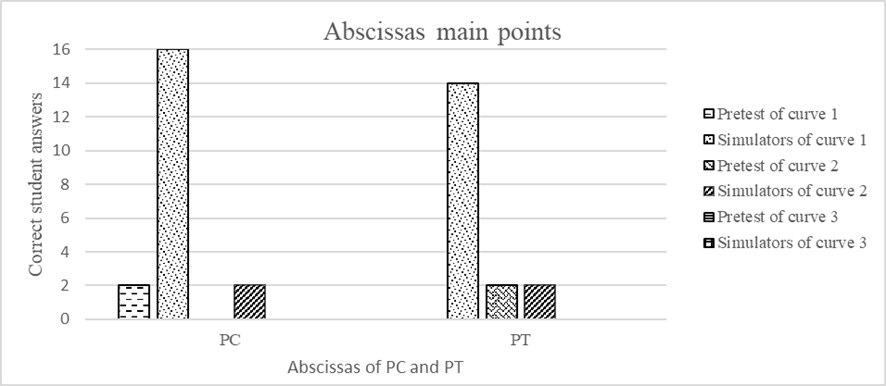 Figure 7:
Correct Answers for the Calculated Abscissas of the
CCS
Figure 7:
Correct Answers for the Calculated Abscissas of the
CCS
Source: Author.
b. Analysis of the
Responses to the Open-Ended Question Sections
After students interacted with the Applet, their responses were analyzed.
Section A explored the effect of the change in direction on the Delta, asking them to describe the changes in the coordinates of PI, PT, and PC, and the reasons for these changes. The following questions were used to assess student understanding: What happens if the Delta changes direction? Describe what happens to the coordinates of PI, PT, and PC. Which coordinates change? Why?
The following criteria were used to analyze the responses in this section:
-
“Understands
the concept”: The student understands that the PT coordinates change due to
the change in direction, while the PC and PI coordinates remain the same.
-
“Partially understands”: The student states that
the PC or PI coordinates change along with the PT coordinates or points out a
change in the quadrant of the exit azimuth, without elaborating on the answer
-
“Does not understand the concept”: The student does
not recognize that the PT coordinates change or presents an inadequate focus on
the entry and/or exit azimuths.
-
“No response”: The student does not offer an answer
to the question posed.
Section B inquired about the impact on the geometric elements of the curve when changing the radius, asking them to describe these changes. To assess students’ understanding of this concept, the following questions were used: What happens to the value of the geometric elements of the curve if the radius is changed? How do they change?
The criteria for analyzing the responses to the questions in this section were:
-
“Understands
the concept”: The student understands that the geometric elements of the
curve change proportionally to the curve’s radius.
-
“Partially
understands”: The student recognizes that the geometric elements of the
curve are affected by the change in radius but does not provide a detailed
explanation.
-
“Does
not understand the concept”: The student fails to adequately express how
the changes occur or relate them to another element of the curve.
-
“No
response”: The student does not offer a response to the question posed.
 Figure 8: Analysis of Responses to Open-Ended Questions in Sections
A and B
Half of the students partially understand the
change in the curve’s coordinates when the curve’s direction changes, and a
quarter of the students understand the concept.
Figure 8: Analysis of Responses to Open-Ended Questions in Sections
A and B
Half of the students partially understand the
change in the curve’s coordinates when the curve’s direction changes, and a
quarter of the students understand the concept.
Source: Author.
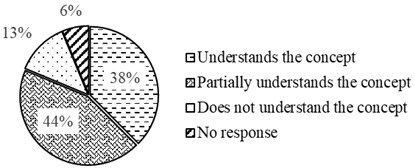 More than a third of the students understand the
geometric changes of the curve if the radius changes; however, a fifth do not
understand the changes or did not respond.
More than a third of the students understand the
geometric changes of the curve if the radius changes; however, a fifth do not
understand the changes or did not respond.
Source: Author.
Table 3 contains the
analysis of the responses to the open questions in sections C and D.
Table 3:
Analysis
of Responses to Open-Ended Questions in Sections C and D
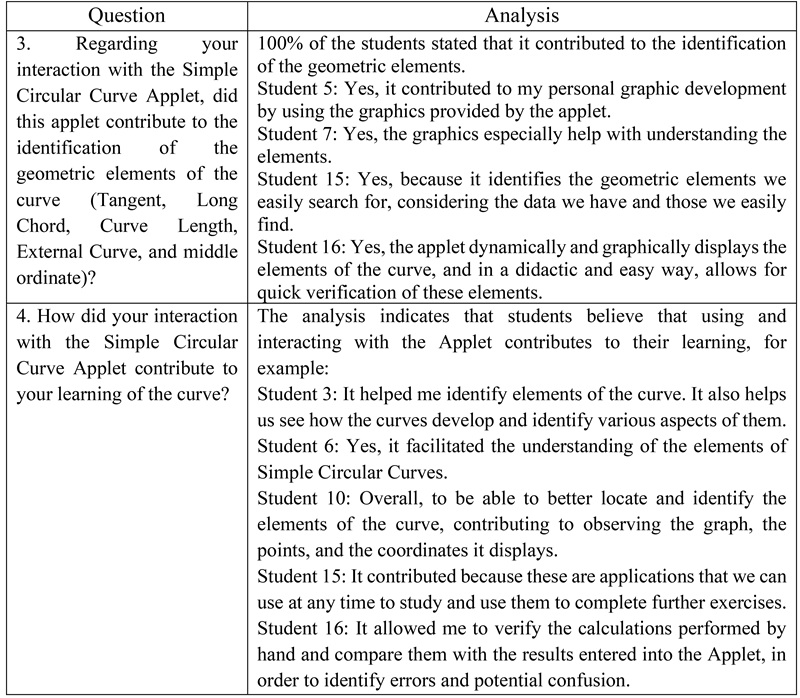
Source: Author.
The results also reveal that students were able to interact with the Applets in a way that allowed them to obtain data that helped them understand the topic of SCC. However, according to the results in Table 3, some students experienced difficulty understanding concepts related to calculating azimuths and the direction of the curve, which prevented all of them from obtaining the geometric elements of the third curve.
Conclusions
The main conclusions of this study are as follows: 1) The planning, implementation, and evaluation of the teaching-learning proposal had a positive impact. The students’ performance improved, as those who initially had difficulties in the pretest were able to refine their responses after interacting with the Apps, especially in determining delta angles and the coordinates of the main points. 2) The development of the teaching sequence contributed to the teacher’s investigative training by integrating technology into the classroom for teaching the Simple Circular Curve. 3) The students demonstrated metacognitive processes by reflecting on and being aware of their own learning processes, which validated the hypothesis proposed in the study.
Acknowledgments
We would like to thank
Professor Rubby Estela Pardo Pinzón, professor of the Roadway Topography course
in the Surveying Technology program, for designing the pretest and for her
collaboration in conducting the class.
References
[1] E. Sáenz, M. Patiño y J. Robles, «Desarrollo de las competencias matemáticas en el pensamiento geométrico, a través del método heurístico de Pólya», Panorama, vol. 11, nº 21, pp. 53–67, 2017.
[2] C. Álvarez-Melgarejo, J. Cordero-Torres, J. González-Bareño y O. Sepúlveda-Delgado, «Software GeoGebra como herramienta en enseñanza y aprendizaje de la Geometría», Educación y Ciencia, vol. 22, pp. 387-402, 2019.
[3] J. W. Patiño Delgado, Estrategia pedagógica mediada por GeoGebra para el aprendizaje del pensamiento geométrico, Barranquilla : Universidad de la Costa CUC, 2021.
[4] P. Suárez, A. Salamanca y A. Jaime, «Estrategias Mediadas por TIC para Desarrollar el Pensamiento Espacial y los Sistemas Geométricos», Voces y Realidades Educativas, vol. 1, nº 1, pp. 99-114, 2018.
[5] M. J. Cuetos Revuelta, L. Grijalbo Fernández, E. Argüeso Vaca, V. Escamilla Gómez y R. Ballesteros Gómez, «Potencialidades de las TIC y su papel fomentando la creatividad: percepciones del profesorado», Revista Iberoamericana de la Educación Digital, vol. 23, nº 2, pp. 287–306, 2020.
[6] M. Macías Rojas, E. O. Caro y F. H. Fernández Morales, «Las mediaciones TIC en la resolución de problemas matemáticos, un abordaje documental», Revista Gestión y Desarrollo Libre, vol. 7, nº 14, pp. 1-23, 2022.
[7] A. Grisales, «Uso de recursos TIC en la enseñanza de las matemáticas: retos y perspectivas», Entramado, vol. 14, nº 2, pp. 198-214, 2018.
[8] J. Padilla-Beltrán, P. Vega-Rojas y D. Rincón-Caballero, «Tendencias y dificultades para el uso de las TIC en educación superior», Entramado, vol. 10, nº 1, pp. 3938–3944, 2014.
[9] L. Quiroga, O. Vanegas y S. Jaramillo, «Ventajas y desventajas de las tic en la educación “Desde la primera infancia hasta la educación superior”», Revista de Educación y Pensamiento, vol. 26, pp. 77–85, 2019.
[10] C. H. Chivai, A. A. Soares and P. Catarino, «Application of GeoGebra in the Teaching of Descriptive Geometry: Sections of Solids,» Mathematics, vol. 10, nº 3034, pp. 1-15, 2022.
[11] L. Stenhouse, Investigación y desarrollo del currículum, Madrid: Ediciones Morata S. A., 1984.
[12] R. Hernández Sampieri, C. Fernández Collado y M. D. P. Baptista Lucio, Metodología de la Investigación, sexta ed., México, D.F.: McGraw Hill, 2014.
[13] Instituto Nacional de Vías, Manual de Diseño Geométrico de Carreteras, Bogotá: INVIAS, 2008.
[14] P. Wolf y C. Ghilani, Topografía, decimocuarta ed., México, D.F.: Alfaomega, 2018.
[15] J. Cárdenas, Diseño geométrico de vías, tercera ed., Bogotá: Ecoe Ediciones, 2020.
Notes
*
Research article
Author notes
a Corresponding author. E-mail: joblanco@unal.edu.co
Additional information
How to cite this article: O L Godoy Morales, J S Blanco
Rincón, M Garzón Vargas, J H Bonilla Romero, “Teaching & Learning Proposal
for a Simple Circular Curve in Roads using GeoGebra” Ing. Univ. vol. 29, 2025. https://doi.org/10.11144/Javeriana.iued29.tlps