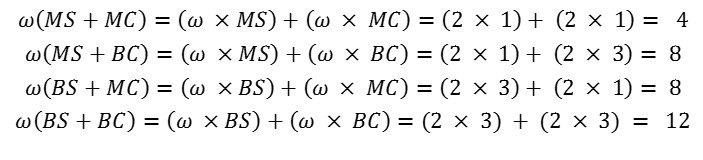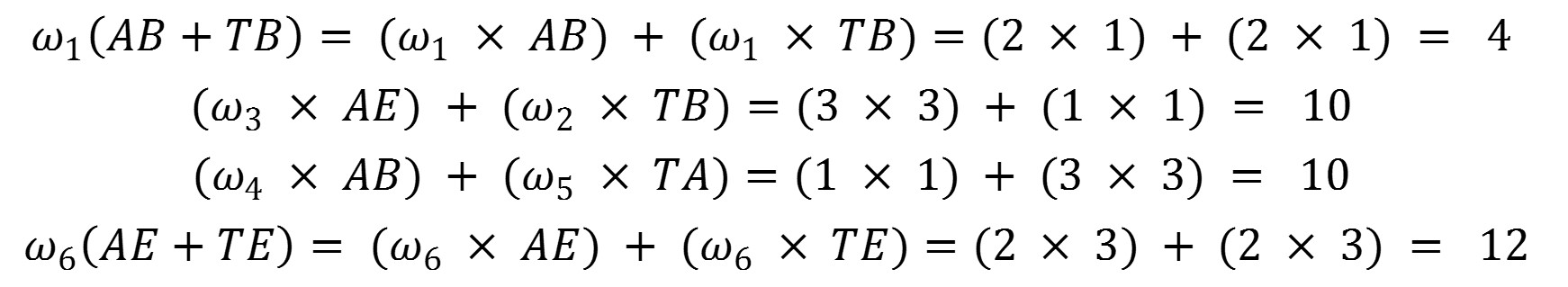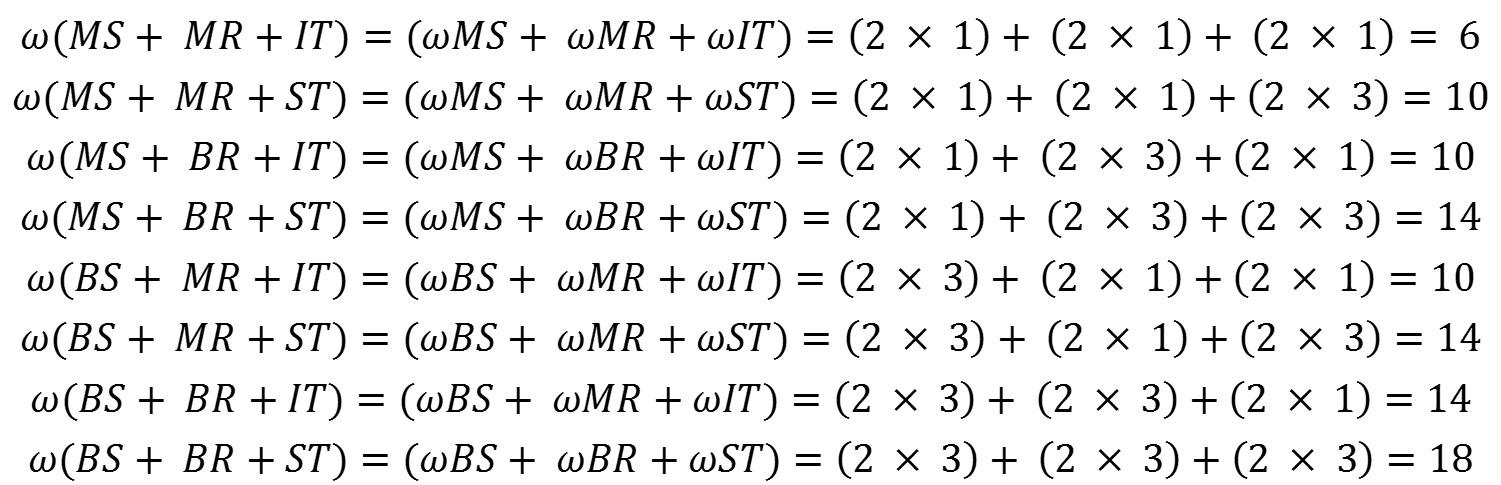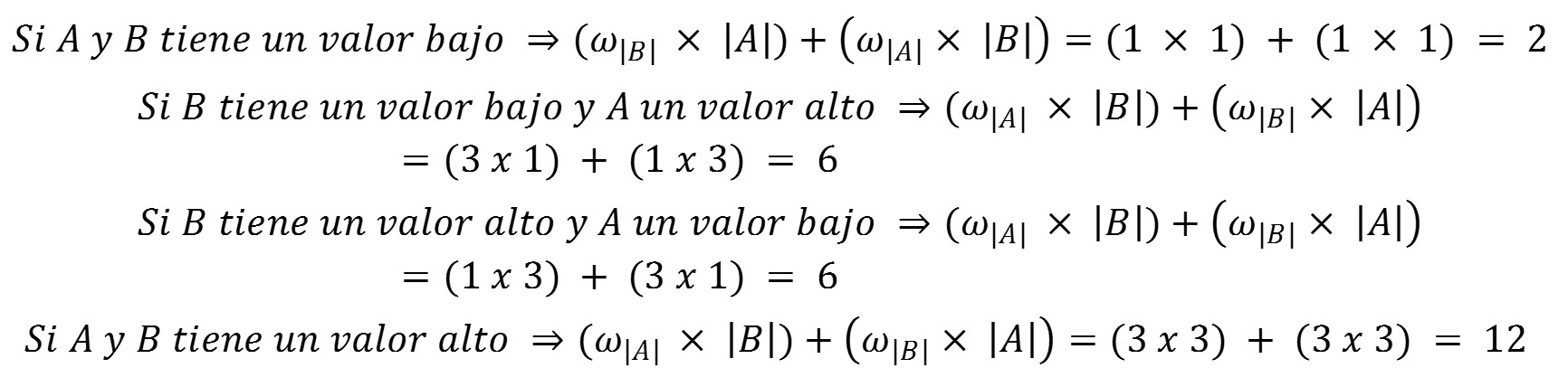La Teoría Funcional de la Cognición está concebida principalmente como una teoría del juicio en la vida cotidiana (Anderson, 1991, 1996, 2008). Comúnmente, nuestros procesos cognitivos se ven expresados en los múltiples juicios que emitimos sobre la realidad inmediata o sobre algunos aspectos de dicha realidad. Por ejemplo, antes de levantar un objeto pesado, rápidamente consideramos su peso, esto con el fin de calcular y hacer el esfuerzo necesario para no poner en riesgo nuestra columna vertebral. Asimismo, antes de comprar una camisa, las personas juzgamos la conveniencia del producto para satisfacer nuestras necesidades reales. Esta decisión sobre la conveniencia de la camisa está, en principio, en función del precio, la calidad aparente de la tela, el color y muchas otras características basadas en nuestra historia de aprendizajes y en las interacciones con nuestro contexto. De igual forma, quien lee este artículo se encuentra actualmente en el proceso de juzgar la conveniencia de continuar con la lectura. Su juicio depende del abordaje del tema general, de la calidad de la escritura y de las condiciones de comodidad en las que el lector se halle. Así como en los ejemplos anteriormente nombrados, la lista de eventos en los que podemos emitir un juicio es infinita.
Esta idea de que la actividad psicológica es básicamente una actividad de juicio (o de toma de decisiones) o, en otras palabras, una actividad de integración de la información, ha estado presente desde los inicios del desarrollo de la psicología. Janet (1889), por ejemplo, habla de “la agregación psicológica” como proceso central de la actividad mental. Para el autor, el cerebro humano produce continuamente síntesis mentales de múltiples sensaciones (y pensamientos asociados) dirigidos a estas (o los crea). Así, el propósito de este artículo teórico es presentar una metodología general para el estudio de los juicios en la vida cotidiana, y de manera más específica, exponer una serie de estudios desarrollados hasta el momento que ilustran la manera como operan las reglas psicológicas cuando de emitir un juicio se trata. Dichos juicios corresponden a situaciones de la vida cotidiana y se han estudiado a profundidad en escenarios asociados a la salud, la política, la economía, la ética, etc.
La Teoría Funcional de la Cognición (Anderson, 1981, 1982) busca –y ha
buscado desde sus orígenes– establecer una teoría del juicio en la vida
cotidiana. Su objetivo es explicar las reglas básicas que usamos todos los días
para emitir juicios. Los ejemplos de situaciones de juicios en la vida
cotidiana son ilimitados y por esto, las aplicaciones de la teoría, de alguna
manera, tampoco tienen límites.
Conceptos básicos de la Teoría Funcional de la Cognición
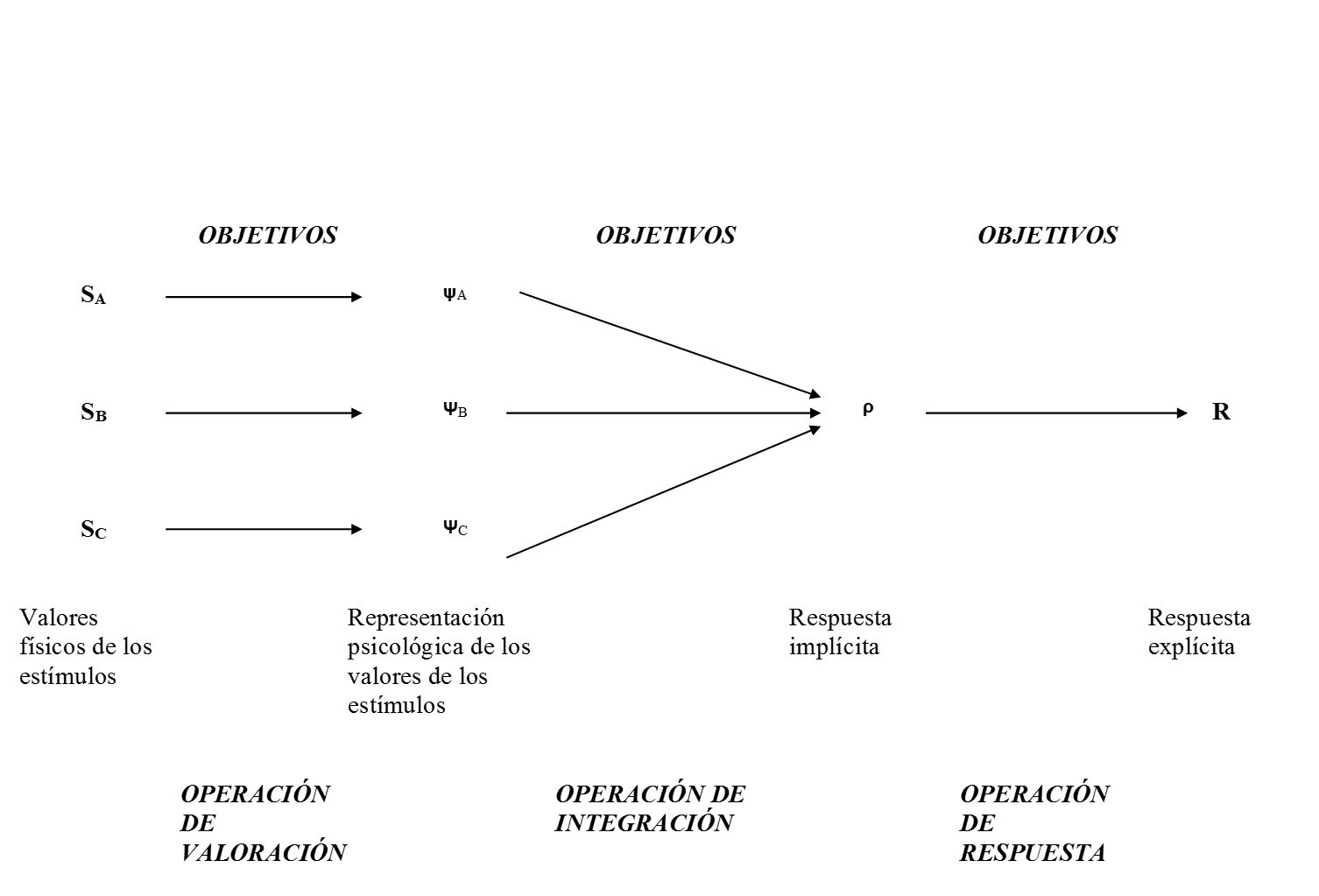
La Figura 1 muestra el diagrama de integración de la
información propuesto por Anderson (1981, 1982). En este diagrama, se puede
observar un campo de estímulos externos (SA, SB que se
somete a tres operaciones sucesivas: (a) la operación de valoración, que
corresponde a la representación psicológica de cada estímulo SA en
un ψA;
(b) una operación de integración que agrupa estas representaciones psicológicas
en una respuesta implícita ρ y (c)
una operación de respuesta que a partir de una respuesta implícita pasa a ser
una respuesta observable o explícita R.
En el Diagrama de Integración de la Información, aparecen de manera explícita
el estado inicial y los objetivos propios del sujeto. Los tres operadores:
valoración, integración y respuesta se rigen por los objetivos del sujeto. Este
diagrama también ilustra dos aspectos clave de los juicios: la toma de
decisiones enfocada hacia un objetivo y el carácter multifactorial de dicho
objetivo.
En detalle, el concepto de la valoración expresa de forma más específica la búsqueda de un fin o el alcance de un objetivo y el contexto en el que se da cualquier actividad de juicio. El concepto de valoración utilizado por Anderson para describir un operador o una función no podría definirse exactamente como una evaluación, ni una estimación de un estímulo externo (Si) realizada por el sujeto, más bien debería entenderse como la creación de un valor subjetivo. La valoración es el proceso que regula la creación de una representación que está en función tanto del propósito como de las experiencias personales vividas por quien emite el juicio.
El tipo de informaciones creado a partir de la valoración es tal que los valores resultantes discriminados quedan listos para ser integrados. El valor del parámetro ψ no es constante en los estímulos; depende tanto de la perspectiva desde la que se ha hecho el juicio (el propósito especial asignado a la tarea) y también, por lo general, del estado de motivación y/o emoción del sujeto. La operación de valoración da a los estímulos externos SA, SB y SC (que pueden ser estímulos físicos o sociales) un sentido psicológico, expresado en términos de escala de valores (Escalas de valores ψA, ψB, ψC).
Para ilustrar lo anterior, supongamos que SA, SB, SC son los elementos de una situación en la que se desea comprar una prenda de vestir. SA, podría ser la calidad (durabilidad): muy buena. SB, el precio de la prenda: precio alto. SC, el aspecto estético de la prenda de vestir: no muy bonita. Estos tres estímulos son inconmensurables, hacen parte de categorías distintas del mismo producto (calidad, precio y estética) y también se miden de manera diferente. Dicho esto, antes de que opere la integración –de acuerdo con la teoría–, se debe poder asegurar la conmensurabilidad de esos estímulos para que puedan ser operados en una misma escala de medida, la cual se establece dependiendo del objetivo, en este caso el objetivo es comprar una prenda de vestir. El objetivo no es lavar o vender la prenda, entonces, la escala a través de la que se busca una respuesta, o un juicio, se definirá en términos de aceptabilidad, en otras palabras, de qué tan atractivo resulta el producto para el consumidor.
El estímulo “calidad” (S1) se asocia con un cierto grado de atractivo (ψ1): atractivo alto. Del mismo modo, los estímulos “precio alto” y “no muy bonito” (S2 y S3) se relacionan con otros dos valores (ψ2 y ψ3), respectivamente. El grado de atracción se clasificaría en moderado y bajo. A las funciones que relacionan S1, S2 y S3 con ψ1, ψ2 y ψ3 se les denomina funciones de valoración. Las formas de estas funciones pueden ser muy diferentes. En el ejemplo, las funciones ƒ1 y ƒ3 pueden ser funciones constantes y crecientes. Por una parte, si la calidad es buena y el componente estético es aceptable, entonces, el atractivo sobre el producto también será grande. En contraste la función ƒ2 podría comportarse de manera diferente a ƒ1 y ƒ3, mostrando una función constante decreciente. Cuanto más alto sea el precio, menor será el atractivo por el producto. Pero, en general, no se excluye que algunas funciones sean, para algunas personas, funciones logarítmicas (véase, por ejemplo, Muñoz Sastre & Mullet, 1998). También se puede esperar que algunas funciones sean de tipo umbral. Más allá de un determinado valor de S2, por ejemplo (precio), el valor ψ2 equivalente no se modificaría más; debajo de este valor, ψ2 sería conexo (linealmente) a S2.
El segundo proceso es el de integración. Una vez realizada la etapa de valoración que asegura la conmensurabilidad de diversos estímulos (S1, S2, S3), los valores subjetivos ψ1, ψ2 y ψ3 se integran para producir una unidad de respuesta unitaria, así internamente el sujeto da una respuesta implícita ρ. Por consiguiente, en esta fase es donde se da lugar a la integración de las valoraciones, donde podrían generarse múltiples respuestas implícitas ρ. Por consiguiente, el operador de integración es donde se genera el paso de determinación múltiple de la respuesta singular ρ. El concepto de integración refleja el carácter multifactorial de todo tipo de juicios.
En el momento de la integración, los valores de la escala pueden recibir diferentes pesos ωi, lo que refleja la importancia de las diversas fuentes de información que el sujeto utiliza. En nuestro ejemplo sobre el juicio para escoger una pieza de ropa, el peso ω1 está asociado a la escala de valor de calidad, y podría por ejemplo, ser el doble del peso ω2, asociado con el valor de la escala de precio. El peso de la estética puede ser cero, por ejemplo, de ser así, se considera que este aspecto no tendría por qué intervenir en la compra de una prenda.
En algunos casos, el peso ω1
es independiente del valor de la escala ψ1. Sin embargo, en
otros, a cada valor en particular corresponderá un peso diferente. Continuando
con el ejemplo de la pieza de ropa, uno puede hacerse una idea de lo
mencionado, si por ejemplo, cuando S1 y los valores ψ1
(calidad) son muy bajos, el peso ganado por el valor de la escala
correspondiente a este estímulo es muy importante. Cualquiera que sea el precio
o la estética de la prenda de vestir, si ψ1 es baja, es
decir, si la pieza no es de buena calidad, por lo general, el nivel de
atracción por el producto seguirá siendo muy bajo. A la inversa, cuando S1
y ψ1 son valores de orden medio, entonces el peso de este
estímulo puede ser más limitado, así el precio y la estética serán un poco más
determinantes. En el momento de la integración, también los valores de la
escala pueden desempeñar diferentes roles. En algunos casos, la integración se
realiza siguiendo una ley de suma, de promedio o de sustracción, en el que el
papel del estímulo fue el mismo, es decir, que un valor de una escala
simplemente se añade o se resta a otro. En otros casos, en donde la integración
se realiza mediante la multiplicación, la situación es diferente. Uno de los
valores puede actuar tomando el valor del peso de otro valor.
Finalmente, de acuerdo con el Diagrama de Integración de la Información,
se encuentra la respuesta. Después de las operaciones de valoración y de
integración, en una tercera etapa, la respuesta predeterminada ρ se transforma en una respuesta
explícita R, usando el operador de
respuesta (R). La respuesta
explícita puede ser una expresión facial, una respuesta fisiológica, motora o
verbal. Aquí, en general, se trata de la selección de un nivel a lo largo de
una escala de juicio. La unidad de función de ρ y R se denomina
función de respuesta o función motora. Cuando esta función es lineal, el
estudio del proceso de integración se simplifica en gran medida, sin embargo,
este no es el caso más frecuente.
La regla aditiva
La regla aditiva, al menos en apariencia, es la más básica. Esta regla supone que en el proceso de integración de información que conduce a un juicio, los diferentes elementos de información simplemente suman sus efectos. En otras palabras, esta regla supone que el efecto sobre el juicio final de cada elemento es independiente del efecto de otros elementos de información que forman el contexto en el cual se hace el juicio. Esto es porque los valores iniciales de cada ψi se mantienen, independientemente de que otros se agreguen, por supuesto se suman, pero los valores se mantienen intactos.
Se puede observar en la Figura 2 una ilustración de la regla aditiva. Es una situación de juicio de satisfacción con la vida a partir de dos índices, el grado de acuerdo con el cónyuge y la salud física. El eje vertical representa el grado de satisfacción general y el eje horizontal muestra dos grados de salud física considerados. Las dos líneas continuas corresponden a los dos grados de acuerdo con el cónyuge. Cada punto corresponde a una configuración de la información, es decir, a una situación concreta de juicio: mala comprensión (MC) y mala salud (MS), buena comprensión (BC) y mala salud (MS), mala comprensión (MC) y buena salud (BS) y, en última instancia, buena comprensión (BC) y buena salud (BS). Las líneas son aproximadamente paralelas. Esto demuestra la aditividad de los efectos.
La lógica de los efectos de la regla aditiva es la siguiente: vamos a suponer que 1 y 3 son los valores correspondientes al grado de satisfacción de las modalidades del primer factor (acuerdo con el cónyuge) y 1 y 3, también son los valores correspondientes al grado de satisfacción de los niveles del segundo factor (salud física). Estos valores correspondientes provienen de la operación de valoración. Esto es lo que también se ha llamado valores de la escala. Supongamos, para hacer más sencillo este ejemplo, que los pesos de los dos factores son iguales. Si el peso ω de cada factor se fija en 2, se obtienen los cuatro valores siguientes:
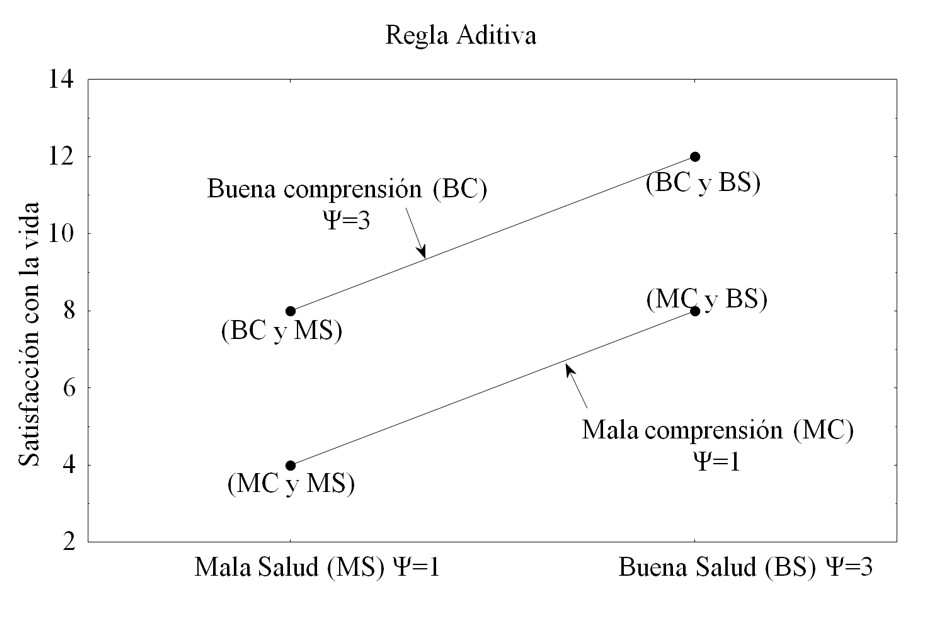 Figura 2
Ilustración
de la regla aditiva
Figura 2
Ilustración
de la regla aditiva
Fuente: elaboración propia.
Las diferencias entre los cuatro valores tomados por pares son constantes: 12 - 8 = 4 y 8 - 4 = 4. El paralelismo de las líneas expresa esta constante. Si una experiencia de juicio se lleva a cabo de acuerdo con el principio descrito anteriormente, si los resultados están organizados como se muestra en la Figura 2 y si hay líneas paralelas, entonces es correcto decir que la regla juicio que se utiliza es la aditiva.
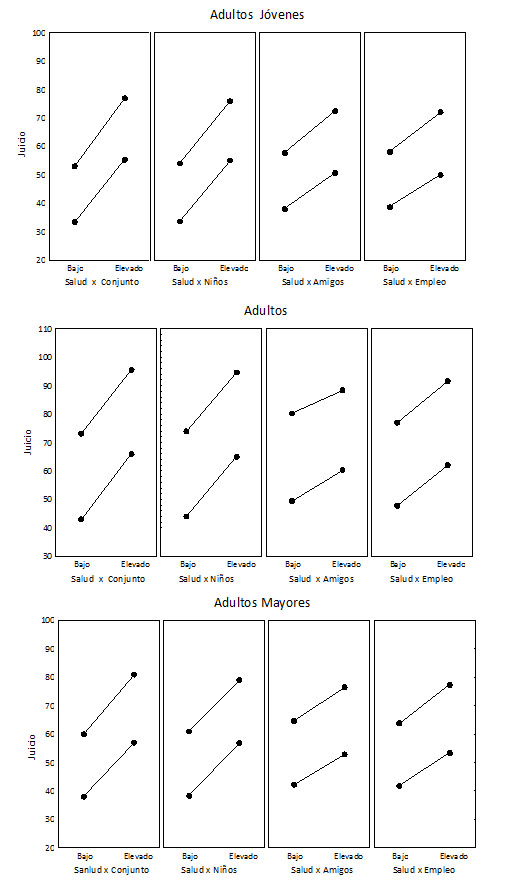
El estudio realizado por Muñoz Sastre (1999) deja ver la facilidad con que los estudios sobre las reglas de los juicios implementadas en la vida cotidiana, pueden llevarse a cabo con éxito (véanse también, Ahmed, Azar, & Mullet, 2007; Macri & Mullet, 2003; Makris & Mullet, 2003; Marquié, Sorum, & Mullet, 2007). Durante el estudio de Muñoz Sastre (1999), no había dos, sino seis factores de información que se proporcionaron a los participantes, en la forma de escenarios. Una pequeña parte de los resultados se presenta en la Figura 3. Lo que más resalta en sus hallazgos, es el paralelismo casi sistemático de los patrones de integración, independientemente de la muestra de individuos considerada. También se pueden observar las diferencias en las pendientes y en las distancias entre las líneas, de un panel a otro y de una muestra a otra, que proporcionan información sobre la importancia relativa de cada factor y cada nivel de edad, en comparación con otros factores.
La regla disyuntiva
La regla disyuntiva es un poco más compleja que la regla aditiva. Se supone que en el proceso de integración de información que conduce al juicio, los diferentes elementos simplemente no cumplen efectos aditivos. En otras palabras, esta regla de disyunción supone que el efecto de cada elemento sobre el juicio depende de otra información que va formando el contexto en el cual se hace el juicio, es decir, en el que se procesa este elemento en particular. Esta regla supone que el peso asignado a un elemento de información en este proceso es proporcional a su valor relativo.
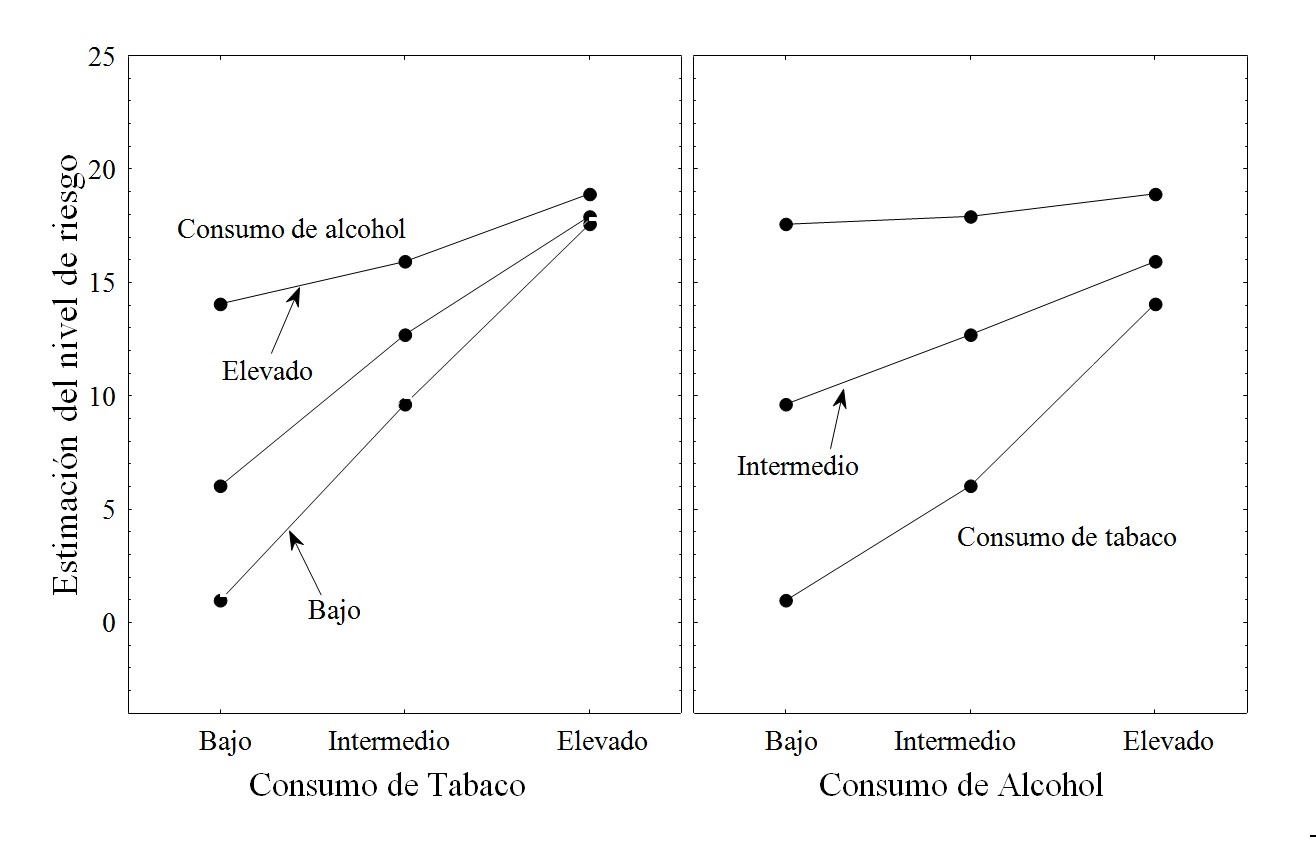
Como ejemplo de lo dicho, la Figura 4 ilustra la regla disyuntiva. Esta figura muestra una situación en la que se estudia la estimación de riesgo para la salud a partir de dos índices de nivel: de consumo de alcohol y de consumo de tabaco. En el eje vertical, está el juicio de estimación de riesgo. A lo largo de los ejes horizontales se organizan dos grados de consumo de tabaco. Las dos líneas continuas corresponden a los dos grados de alcohol considerados. Cada punto corresponde a una configuración de información, es decir, una situación concreta del juicio: bajo consumo de ambas sustancias (tabaco y alcohol), bajo consumo de tabaco y el consumo excesivo de alcohol, fumar en exceso y bajo consumo de alcohol y alto consumo de las dos sustancias. Como se observa, las líneas no son paralelas, convergen hacia la derecha. Esto demuestra los efectos disyuntivos en el juicio.
La lógica de la regla disyuntiva es la siguiente: en el ejemplo anterior
(sobre la regla de la suma), se asumió que 1 y 3 eran los valores
correspondientes al grado de satisfacción, proporcionado a los términos de los
dos factores considerados. Los cuatro valores correspondían a las cuatro
combinaciones de los dos factores, esto era para cuando se aplicaba un modelo
aditivo y con pesos iguales (con valores fijos en 2): 4, 8, 8 y 12. Las
diferencias entre los cuatro pesos tomados por pares fueron constantes. Bajo el
modelo disyuntivo, por el contrario, el peso de un elemento de información
depende del valor del otro (s) elemento (s). Tomemos el caso de dos elementos
de valor que pueden ser considerados idénticos: bajo nivel de consumo de tabaco
(TB) y bajo nivel de consumo de alcohol (TA), o elevado nivel del consumo de
tabaco (TE) y el elevado nivel de consumo de alcohol (AE). Como en el ejemplo
anterior, se fijarán los pesos en 2 (ω1
y ω6 =2). Sea el
caso de dos elementos de valor que pueden ser considerados como diferentes
(bajo nivel de tabaquismo y elevado de alcohol, o de alto nivel de consumo de
tabaco y bajo consumo de alcohol), en ese mismo sentido, el peso de cada uno de
los dos factores será diferente. La aplicación de la regla disyuntiva supone
que el elemento con el valor más pequeño también recibe el peso más pequeño que
nosotros estableceremos en (si TB = 1 → ω2 = 1; si AB = 1 → ω4 = 1), y el elemento con el valor
más alto recibirá el mayor peso que vamos a establecer como (si AE = 3 → ω3 = 3; si TA = 3 → ω5 = 3).
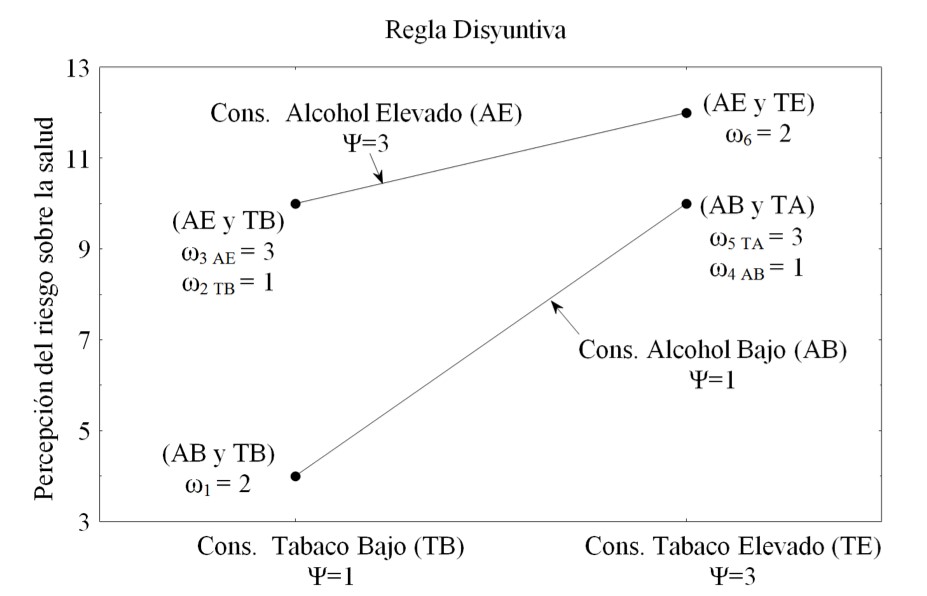 Figura 4
Ilustración
de la regla disyuntiva
Figura 4
Ilustración
de la regla disyuntiva
Fuente: elaboración propia.
Si se consideran los niveles de consumo de la
sustancia, teniendo en cuenta los mismos valores que en el ejemplo anterior (1
y 3), un simple cálculo proporcionará los siguientes cuatro valores
resultantes:
Las diferencias entre los cuatro valores tomados por pares no son constantes: 12 - 10 = 2 y 10 - 4 = 6. También como se observa en la Figura 4, las curvas no son paralelas y esto da cuenta de que no se mantiene un valor constante. La forma de abanico abierto hacia la izquierda, muestra cómo funciona la regla disyuntiva. Así, si un juicio se lleva a cabo de acuerdo con el principio descrito anteriormente, si los resultados están organizados como se muestra en la Figura 4 y si hay una convergencia de las líneas hacia la derecha, entonces es razonable afirmar que la regla con la que se está procesando el juicio es la disyuntiva.
El estudio realizado por Hermand, Mullet y Lavieville, 1997, (véanse también Hermand, Mullet, & Coutelle, 1995; Hermand, Mullet, Sorum, & Tillard, 2000), cuyos resultados se presentan en la Figura 5, ilustran particularmente bien la naturaleza inesperada de las reglas de juicio implementado en ciertas situaciones de la vida cotidiana. En este estudio, se consideraron diferentes niveles de consumo de alcohol y tabaco (bajo, moderado y alto). La Figura 5 (en el panel izquierdo) muestra que cuando el consumo de tabaco es bajo o cero (ilustrado en el eje X), el aumento del riesgo (que se mide en el eje Y) asociado con el consumo de alcohol (representado por las líneas) tiende a ser muy alto (evidente en la notable distancia de las líneas que representan las diferencias en la estimación de los niveles de riesgo). Por el contrario, si el consumo de tabaco es alto, el aumento del riesgo asociado con el consumo de alcohol tiende a ser muy bajo (evidente en el reducido espacio entre las líneas). El panel de la derecha de la Figura 5 muestra los mismos resultados, pero de una manera diferente. Estos son los niveles de consumo de alcohol (presentados en el eje X) y los niveles de consumo de tabaco (representados por las líneas). El patrón de resultados es igualmente ilustrador. Se pueden encontrar en Mullet, Rivière y Muñoz Sastre (2007) otros ejemplos de aplicación de la regla disyuntiva.
La Regla conjuntiva
La regla conjuntiva es la regla simétrica de la regla disyuntiva. Al igual que en la regla disyuntiva, la regla conjuntiva asume que en el proceso de integración de la información que conduce al juicio, los diferentes factores de información no cumplen únicamente efectos aditivos, pero a diferencia de la regla disyuntiva, asume que el peso ganado por un elemento de información es inversamente proporcional al valor inicial de este elemento.
La Figura 6 es una ilustración de la regla conjuntiva, que muestra la estimación de la intención de emigrar a otro país en función de la diferencia de salarios entre los países de origen y los países de acogida, además señala la probabilidad de encontrar un trabajo en el país de acogida. El eje Y es el juicio de intención de emigrar, mientras que en el eje X indica dos niveles de probabilidad para encontrar un trabajo en el país de acogida: baja probabilidad (BP) y elevada probabilidad (EP). Las dos líneas corresponden con dos diferencias de los salarios: dos veces el salario promedio en el país de residencia actual (DS) y cuatro veces el salario en el país de residencia actual (CS). Cada punto corresponde a una configuración de información, es decir, una situación concreta de juicio: baja probabilidad de encontrar empleo y dos veces el salario (BP + DS), baja probabilidad de encontrar empleo y cuatro veces el salario (BP + CS), elevada probabilidad de encontrar trabajo y el doble del salario (EP + DS) y elevada probabilidad de encontrar trabajo y cuatro veces el salario (EP + CS). Como se observa las curvas no son paralelas y divergen hacia la derecha. Esto representa los efectos de conjunción en el juicio.
La lógica de la regla conjuntiva es, en parte, la regla inversa de la
disyuntiva. Bajo el modelo conjuntivo, el peso de un factor de información
depende del valor del (los) otro(s) elemento(s). Si se considera el caso de dos
elementos cuyos valores pueden ser considerados idénticos (baja probabilidad de
encontrar empleo (BP) y el doble del salario (DS), o muy alta probabilidad de
encontrar trabajo (EP) y cuatro veces el salario (CS), entonces, el peso de
ambos factores, en virtud de la regla conjuntiva, se encontrarán bajo una ley
idéntica. Ambos factores, tendrán un peso fijo en 2 (ω1 y ω6 =
2). Sea el caso de dos elementos cuyos valores se consideren diferentes (Baja
probabilidad de encontrar trabajo y cuatro veces el salario promedio en el país
de residencia actual, o muy alta probabilidad de encontrar trabajo y dos veces
el salario promedio en el país de residencia actual), entonces, el peso de los
dos factores será diferente.
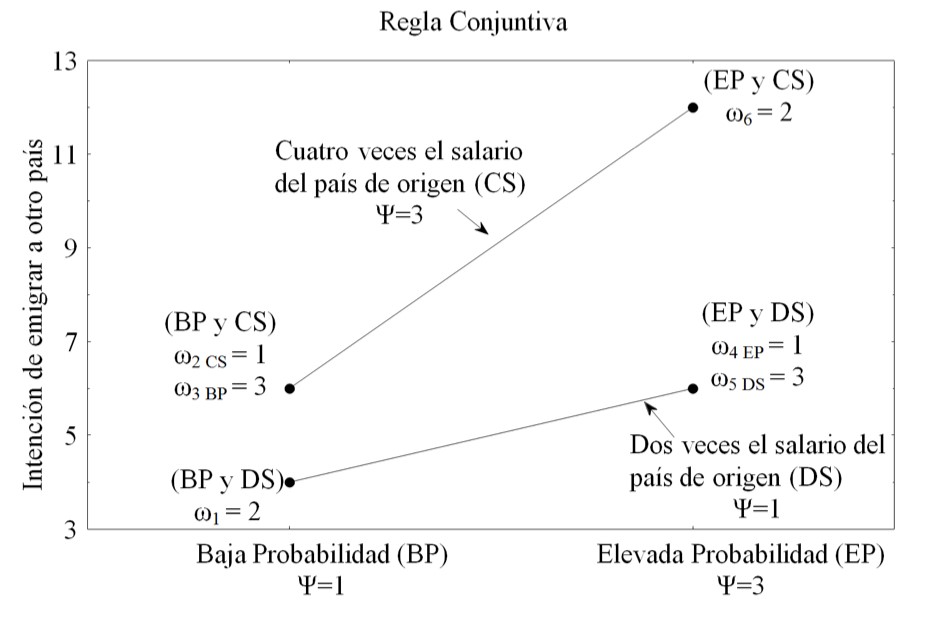 Figura 6
Ilustración
de la regla conjuntiva
Figura 6
Ilustración
de la regla conjuntiva
Fuente: elaboración propia.
La aplicación de la regla conjuntiva supone que el
elemento que tiene el valor más pequeño recibe el mayor peso, es decir (si BP = 1 → ω2 = 3; si CS = 3 → ω3 = 1) y el elemento que tiene el valor más grande recibe el menor
peso, es decir (si EP = 3 → ω4 = 1; si DS = 1 → ω5 = 3). Si los dos factores, oportunidad de
encontrar empleo y diferencia salarial, tomaran los mismos valores del ejemplo
anterior 1 y 3, un simple cálculo proporcionaría los siguientes cuatro valores:
Las diferencias entre los cuatro valores tomados por pares no son constantes: 12 - 6 = 6 y 6 - 4 = 2. La falta de paralelismo de las líneas se ilustra en la Figura 6, donde se observa que los valores de los factores no es constante. Su forma de abanico abierto hacia la derecha, representa la regla conjuntiva. Si una experiencia de juicio se lleva a cabo de acuerdo con el principio descrito anteriormente, si los resultados están organizados de acuerdo con la Figura 6 y si hay una divergencia a la derecha de las curvas, entonces es posible afirmar que la regla de juicio que se utiliza es la conjuntiva.
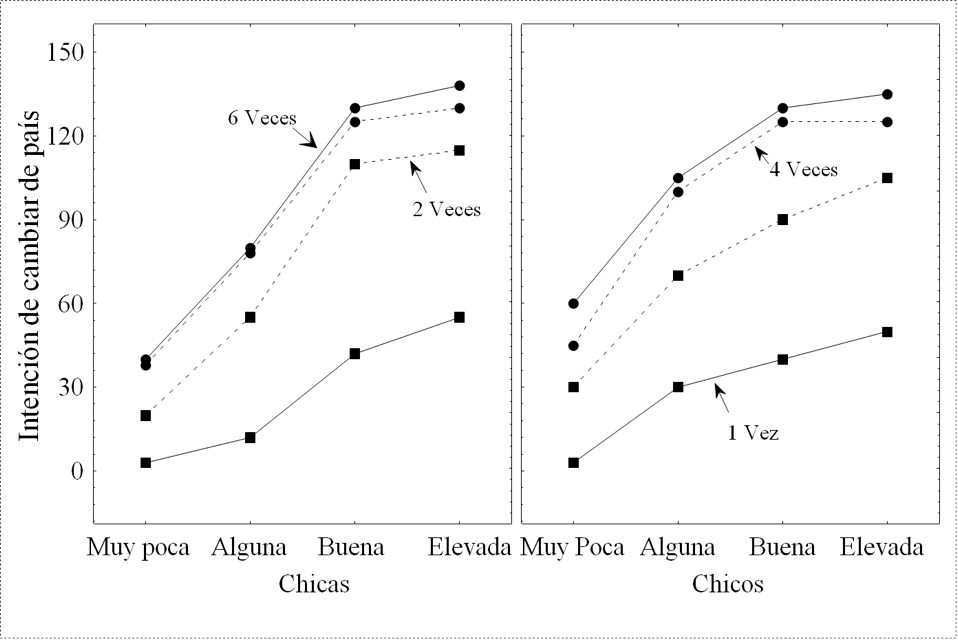
El estudio de Neto y Mullet, 1998, (véanse también Mullet & Neto, 1991) ilustra claramente el papel de la regla conjuntiva en situaciones donde las decisiones son riesgosas; en este caso, la decisión de emigrar para encontrar trabajo en otro país. En dichas situaciones de riesgo, se esperaría que las personas aseguraran la presencia conjunta de una serie de garantías. En este estudio, se consideraron cuatro niveles de probabilidad de encontrar un trabajo (eje X) y cuatro diferencias salariales (líneas). Como se puede observar en la Figura 7, la forma general de los patrones de integración es la de un abanico abierto a la derecha, con independencia del grupo de participantes considerados (niños o niñas). También se evidencia que la mayor parte de la diferencia en la intención de emigrar se produce en la transición entre una y dos veces (en términos de diferencial de salarios) y en especial entre las mujeres participantes.
Se pueden encontrar otros ejemplos de aplicación de la
regla conjuntiva en Muñoz Sastre, Mullet y Sorum (2000) y Simeone, Hermand y Mullet (2001). También
es cierto que, en algunos estudios, la regla disyuntiva y la conjuntiva se
observan conjuntamente en la misma actividad de juicio (Karpowicz Lazreg & Mullet, 2001).
¿Adición o promedio?
Las reglas aditiva, disyuntiva y conjuntiva son aparentemente simples. Sin embargo, ¿qué hay detrás de esta aparente simplicidad? Si se considera en primer lugar el caso de la regla aditiva, se puede observar que coincide con un determinado patrón de resultados que se muestran en la Figura 2. Este es un patrón de paralelismo. De hecho, este patrón de resultados se puede obtener de al menos dos formas diferentes. La primera es la que ya se ha considerado: se asume que 1 y 3 fueron valores correspondientes a los términos de los dos factores considerados en el ejemplo: salud y grado de comprensión con el cónyuge, y que para efectos de facilidad en la comprensión, los pesos son iguales para los dos factores. Se estableció el peso ω = 2 y obtuvieron los siguientes cuatro valores: 4, 8, 8, y 12, así se encontró que las diferencias entre los cuatro valores tomados por pares eran constantes.
Una segunda manera de obtener el mismo patrón de paralelismo con los mismos datos no sería a través de la suma de los valores ponderados, sino mediante el cálculo de los valores promedio ponderados. Tomemos 1 y 3 son los valores correspondientes para los términos de los dos factores (ƒ1 y ƒ2), cada uno con dos niveles. Supongamos de nuevo, por razones de facilidad, pesos iguales de los dos factores, el peso establecido será igual a ω = 2. Mediante el cálculo de promedios, se obtienen los siguientes cuatro valores:
En el caso considerado aquí, como se puede ver en la Figura 8, los
valores finales son muy similares a los del caso anterior: un patrón de
paralelismo. Detrás del mismo patrón de comportamiento de las líneas
(paralelismo), pueden existir diferentes mecanismos de juicios, uno que supone
simplemente la suma ponderada de los valores, la otra, que supone realizar un
proceso de promedio.
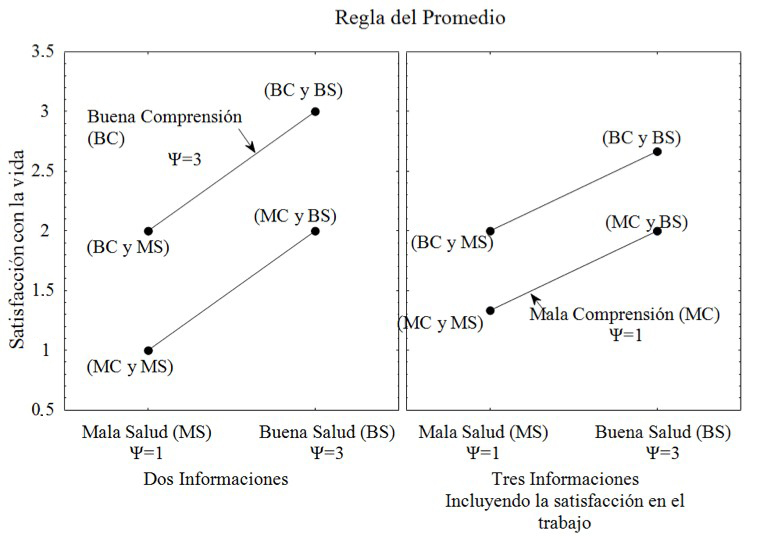 Figura 8
Ilustración
de la regla del promedio (en comparación con la regla sumativa)
Figura 8
Ilustración
de la regla del promedio (en comparación con la regla sumativa)
Fuente: elaboración propia.
En los ejemplos numéricos que ilustran estos procesos, la distinción entre la suma y el promedio es fácil. Los valores resultantes de la suma (de 4 a 12) son significativamente diferentes a los valores resultantes del promedio (de 1 a 3). En un experimento de psicología, por el contrario (ver los tres ejemplos citados en los párrafos anteriores), los valores de las reglas de juicio son cuantías en las que la métrica es arbitraria. Estos se observan a lo largo de escalas de valores de respuesta. Nada garantiza que el valor más bajo registrado o asignado al borde izquierdo de la escala, corresponda a un cero psicológico de los participantes. La única realidad empírica sólida sobre la cual basar las inferencias de la realidad se puede observar en los patrones de los resultados.
Entonces, ¿cómo distinguir los dos posibles procesos subyacentes basándose únicamente en los patrones de respuesta observables? Esto es posible si el dispositivo experimental es complejo. Supongamos que se comunica una tercera parte de la información. En el ejemplo anterior, sobre el criterio del bienestar, este tipo de información podría ser el grado de satisfacción en el trabajo. Por tanto, este dato podría complementar la información sobre el nivel de acuerdo con el esposo y la información sobre la salud.
Siendo 2 el peso establecido para este nuevo elemento y siendo 1 y 3 los valores de los dos términos considerados: el trabajo poco satisfactorio (IT) y de alto nivel de satisfacción con el trabajo (ST), respectivamente. La aplicación de la regla de adición conduce naturalmente a observar los siguientes valores:
Por su parte la aplicación de la regla del promedio
conduce a la observación de los valores resultantes de la siguiente manera:
Los análisis de los cambios de los juicios previamente descritos, permiten decir que estos cambian si se considera un tercer elemento de la información, esto es dependiendo de los juicios resultantes de la aplicación de una u otra regla subyacente. Cuando se aplica la regla aditiva –en el ejemplo de la salud y el acuerdo con el cónyuge–, el valor resultante es 4; cuando se comunica información adicional (trabajo insatisfactorio), el valor resultante pasa de 4 a 6. Cuando se aplica la regla del promedio, en el caso de la mala salud y el desacuerdo con el cónyuge, el valor resultante es 1. Cuando se comunica información adicional, trabajo insatisfactorio, el valor resultante no cambia. Se mantiene el valor de 1. Así que, de acuerdo a la regla de la suma o del promedio, la modificación de la decisión adoptada por un individuo al obtener nueva información no es la misma. De la misma manera, en el caso de una buena salud y un buen acuerdo con el cónyuge, el valor resultante es 12 cuando se aplica la regla aditiva. Cuando se comunica la información adicional, trabajo insatisfactorio, los cambios de valor resultantes pasan de 12 a 14. En el caso de una buena salud y un buen acuerdo con el cónyuge, el valor resultante es 3 cuando se aplica la regla del promedio. Cuando se comunica la información adicional denominada trabajo insatisfactorio, los cambios de valor resultantes van de 3 a 2.33. De tal manera que, dependiendo de si la regla es aditiva o del promedio, la modificación del juicio obtenido con una nueva información idéntica, puede cambiar en sentido positivo de 12 a 14, y en el caso de la ley del promedio, cambiar en sentido negativo de 3 a 2.33.
El proceso que subyace a la regla sumativa resulta muy relevante, puesto que, a pesar de las apariencias, los dos tipos de procesos detrás de la regla sumativa obedecen a diferentes lógicas. A su vez –y como ya se ha anotado antes–, la diferencia entre los dos procesos puede generar resultados opuestos. En otras palabras, si se ignora el proceso subyacente a la regla, podría darse lugar a errores en los juicios. Como se puede observar claramente en la Figura 8, en el panel superior izquierdo (en el que se puede advertir la información de “salud” y “el grado de acuerdo con el cónyuge") las dos curvas son paralelas. En esa misma figura, en el panel superior derecho, cuando se presentan tres informaciones: salud, grado de acuerdo con cónyuge y satisfacción en el trabajo, las dos curvas son paralelas e incrementan las puntuaciones de satisfacción con la vida en comparación con las curvas que se encuentran a la izquierda. Tomadas en conjunto, las cuatro curvas son paralelas y están espaciadas uniformemente. Esta posición relativa de las curvas caracteriza el ajuste en la aplicación de la regla aditiva. En la misma Figura 8, en el panel inferior izquierdo (en el que se muestran los resultados de satisfacción con la vida en función de la información sobre la salud y el grado de acuerdo con el cónyuge) se perciben los resultados cuando se aplica la regla del promedio y allí se puede ver que las dos curvas son paralelas. Cuando se presenta la misma situación, pero con tres informaciones (salud, grado de acuerdo con el cónyuge y satisfacción con el trabajo), en el panel derecho, se puede notar que las dos curvas son paralelas. Estas no superan los niveles de las curvas del panel de la izquierda. Tomadas en conjunto, las cuatro curvas no son paralelas, el espacio entre las líneas no es uniforme. Como se observa, las curvas del panel de la derecha están más cerca entre sí que las del panel de la izquierda. Esta posición relativa de las curvas, la diferencia de espacio entre las líneas y la diferencia en la pendiente caracterizan la aplicación de la regla del promedio.
En la situación que se ha elegido para ilustrar los procesos subyacentes, la regla del promedio parece ser más probable que la regla sumativa (a pesar de su aparente complejidad). Es difícilmente concebible que, para mantener buenas relaciones con el cónyuge, haya que tener una buena salud, pero no estar satisfechos con el trabajo es un factor que podría afectar más la satisfacción con la vida, que mantener una buena relación con su cónyuge y estar sano, y esto es lo que muestra el panel derecho de la regla sumativa en la Figura 8. Es más probable, intuitivamente hablando, que el estado de salud y mantener una buena relación con el cónyuge, pero no estar muy satisfechos con su trabajo, sea una posición menos deseable que simplemente ser saludable y mantener buenas relaciones con su cónyuge, y esto se advierte en el panel derecho de la regla del promedio en la Figura 6.
El estudio de Falconi y Mullet (2003) ilustra claramente la facilidad con la que un proceso de promedio puede ser empíricamente distinguible de un proceso de suma, y las consecuencias prácticas que esta distinción puede tener en una conducta adecuada en un área sensible de estudio. Los participantes debían juzgar el grado de amor que las parejas se tienen basándose en la información sobre estos tres pares de factores: el grado de pasión sentida, el grado de intimidad y el grado de compromiso. En algunas situaciones, sin embargo, algunos factores no fueron incluidos (solo para ver el efecto en la respuesta cuando están o no presentes). La Figura 9 muestra que, para juzgar el grado de amor, los factores pasión e intimidad se combinan en una regla aditiva (según se ve en las líneas punteadas). Esta misma figura muestra que cuando la información del factor grado de pasión no se incluye para el juicio (según la línea continua), la regla observada no es la de la suma, sino la del promedio, esto es porque el efecto del factor intimidad resulta más importante. Es por ello que la curva de trazo continuo tiene una mayor pendiente que cada una de las curvas punteadas (Figura 9).
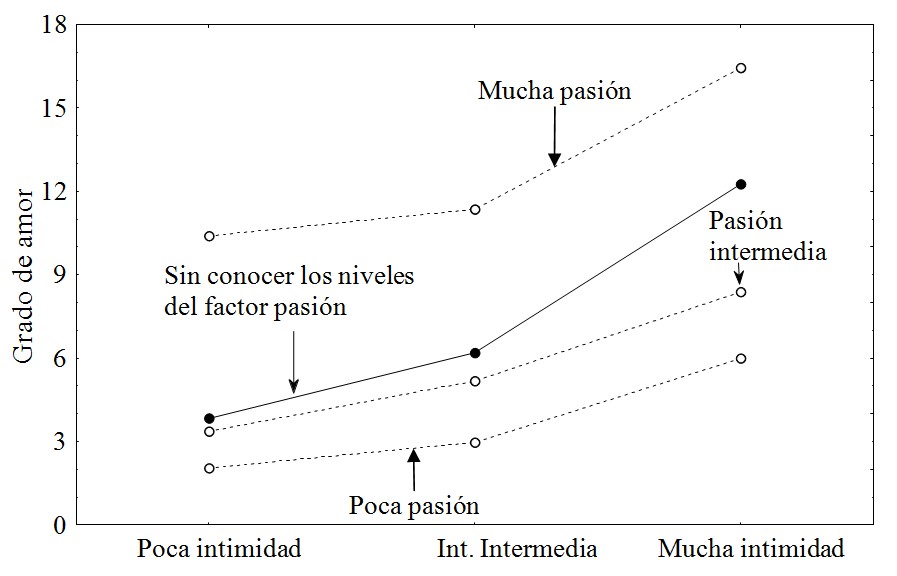 Figura 9
Grado de amor estimado
Figura 9
Grado de amor estimado
Fuente: Falconi & Mullet (2003, p. 285).
Conocer la estructura del modelo mental mediante la cual juzgamos el amor es algo muy importante en la vida. La estructura es estrictamente compensatoria. Si el valor que toma uno de los factores llega a disminuir, esta disminución puede ser compensada por un aumento en el valor de otro factor. Un debilitamiento de la vida privada, como resultado de la separación geográfica puede, por ejemplo, ser compensado con un mayor compromiso fuertemente marcado, socialmente hablando. Si no se conoce exactamente el nivel de la privacidad, entonces se puede juzgar el grado de amor únicamente en función de los otros dos tipos de información. Sin embargo, los factores tienen diferentes pesos (ω). Como puede verse en la Figura 9, las líneas están más ampliamente espaciadas (si se observa el efecto de la pasión) y pendientes (por efecto de la privacidad), luego, una fuerte caída en el nivel de pasión no puede ser completamente compensado por un aumento equivalente en la intimidad.
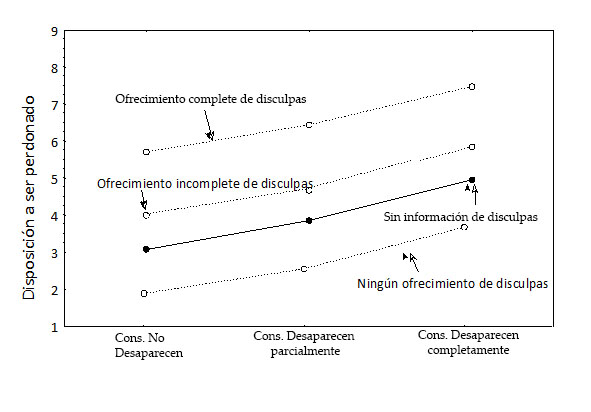
El estudio realizado por Girard, Mullet y Calahan (2002) se puede considerar como otro ejemplo que refleja los resultados observados también en el estudio de Falconi & Mullet (2003). Los autores ilustran la facilidad con la que el proceso de media y el de sumatoria pueden ser distinguidos empíricamente, utilizando la técnica de reducción (o aumento) del número de elementos de información proporcionados. Las consecuencias prácticas de esta distinción se presentan aquí en un ejemplo en el que se habla de la oportunidad de pedir (o no) perdón, a cualquier persona que haya resultado gravemente ofendida y de quienes desean ser perdonados. En el estudio de Girard et al. (2002), se les pidió a los participantes que juzgaran el grado de “disposición a ser perdonado” de varias personas, dependiendo de las circunstancias de un delito cometido. La información adicional proporcionada fue: la intención del daño, la severidad inicial de las consecuencias, el ofrecimiento (o no) de una disculpa por parte del delincuente y la desaparición actual (o no) de las consecuencias. La Figura 10 muestra que el factor de la desaparición actual de las consecuencias afecta la disposición a ser perdonado (pues se observa que las líneas ascienden) y el ofrecimiento de disculpas también tiene un efecto (las curvas se separan). Cuando se presentan estos estímulos, la información se integra en una regla sumativa (líneas paralelas punteadas) y el modelo es claramente el de una suma. Cuando la información sobre el ofrecimiento de disculpas está ausente (línea continua), el efecto del factor de desaparición de las consecuencias no cambia los juicios sobre la voluntad de perdonar. Dada la naturaleza acumulativa de la regla de la integración, un ofrecimiento de disculpas siempre genera un efecto positivo. Del mismo modo, incluso una compensación parcial por daño tendrá un efecto positivo. Si la regla hubiera sido una regla de promedio, un ofrecimiento de disculpas verbal hubiera podido tener un efecto negativo (Ahmed et al., 2007; Azar & Mullet, 2001; Azar, Mullet, & Vinsonneau, 1999; López, Pineda Marín, Murcia, Perilla, & Mullet, 2012, 2013; Vinsonneau & Mullet, 2001).
Es importante tener en cuenta que a veces tanto la regla sumativa como la del promedio están operando en la misma
situación (véanse, por ejemplo, Guillet, Hermand, & Mullet, 2002).
Una variedad de reglas conjuntivas
Al igual que en los efectos sumativos donde pueden coexistir dos tipos de reglas con consecuencias muy diferentes, en la conjuntividad sucede lo mismo. Consideremos en primer lugar el caso de la regla conjuntiva. Esta regla coincide con un determinado patrón de resultados que se muestran en la Figura 6: el de divergencia. Veremos que dicho patrón en realidad se puede conseguir de varias maneras. La primera es la que ya se ha considerado anteriormente, en la que la regla conjuntiva supone que el elemento de información con mayor valor posible recibe el peso más pequeño (será 1) y el elemento con el valor más pequeño de los dos recibe el peso más grande (fijado en 3). Un simple cálculo arrojó los siguientes cuatro valores resultantes: 4, 6, 6, y 12 (véase Figura 6 y apartado de la regla conjuntiva).
Una segunda manera de obtener un patrón de divergencia se logra cuando del peso de cada elemento de información depende del valor absoluto de otro, en lugar de su valor relativo (es decir, superior, igual o inferior) con respecto a este elemento. Sean 1 y 3 los valores-opuestos de los dos términos de cada factor: si el elemento de información B toma un valor bajo, el peso de A será igual a 1; si el elemento de información B toma un valor alto, entonces el peso de A será igual a 3. Igualmente, el peso de B será igual a 1 cuando el valor del elemento A tenga un valor bajo, y el peso de B será 3 cuando A tome un valor alto. Un cálculo simple hace posible obtener los siguientes resultados:
Estos resultados mantienen la forma divergente de los presentados en la Figura 6 y en el apartado de la regla conjuntiva. El obtenido aquí es un patrón de divergencia derecha, que es correcta, incluso más pronunciada que en el caso anterior. Esta diferencia de la divergencia es la que permite distinguir empíricamente entre los dos modelos.
Una tercera forma de obtener un patrón de divergencia se obtiene cuando el peso de cada elemento de la información toma el valor del elemento mismo y no del valor relativo o absoluto del otro, como en los dos casos anteriores. Este tercer método también supone que se aplica la regla promedio y no una regla sumativa. Sean 1 y 3 los valores-opuestos de los dos términos de cada factor; sea 3 el peso de un elemento de información cuando él mismo tiene un contra-valor bajo; sea 1 el peso de cada elemento de información cuando se tiene un contra-valor alto. Así, los cálculos permiten obtener los siguientes valores:
El patrón formado por dichos resultados es, de nuevo, un patrón de divergencia derecha.
La Figura 11 muestra los resultados de la aplicación de la regla conjuntiva presentada anteriormente en la Figura 6. Los datos aquí se han calculado de acuerdo con la tercera forma –explicada en este apartado–, que implican el uso de una regla del promedio. El panel de la izquierda corresponde a los resultados del caso de presentación de dos informaciones; allí las dos líneas son divergentes, la una respecto a la otra. El panel de la derecha, corresponde a una situación en la que se presentan tres informaciones; también en esta ocasión las dos curvas son divergentes una respecto a la otra, sin embargo, son menos divergentes que las del panel izquierdo, su pendiente es menos pronunciada, aunque su posición relativa es comparativamente similar. Esta diferencia en la pendiente y esta menor divergencia caracterizan la aplicación de una regla de promedio en el marco de la regla conjuntiva (Mullet, Ciudat, & Rivière, 2004).
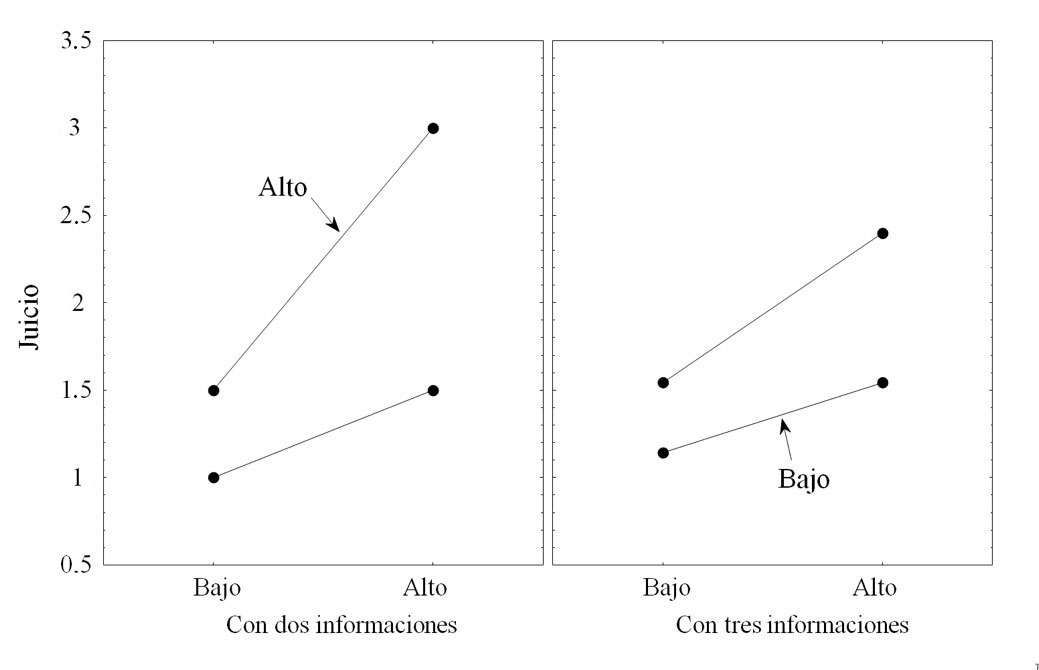 Figura 11
Ilustración de la regla de la conjuntiva promedio
Figura 11
Ilustración de la regla de la conjuntiva promedio
Fuente: elaboración propia.
¿Promedio o multiplicación?
A diferencia de las versiones de las reglas propuestas previamente, la regla de la multiplicación, como su nombre lo indica, supone que el principio integrador de la información no es un principio aditivo (de suma o de promedio), sino un principio de multiplicación. Como parte de la aplicación de la regla de la multiplicación, la condición de los elementos de información difiere de las anteriores: uno de los elementos de información tomará el rol de peso ω con respecto al otro. Mientras que en todas las reglas descritas anteriormente, cada elemento de información recibía un peso particular, constante en el caso de la regla aditiva y variable en el caso de las reglas disyuntivas y conjuntivas.
Se puede encontrar en la Figura 12 (panel superior) la ilustración de la regla multiplicativa. En este caso, se presenta la estimación del grado de aversión (lo contrario de la atracción) al riesgo asociado con situaciones de peligro físico, en el que se plantea el problema de si utilizar o no la resucitación cardiopulmonar (RCP). La estimación del grado de aversión opera a partir de dos índices: la probabilidad de estar en uno u otro de los estados que se sabe que preceden a la reanimación (10 % probabilidad (BP) y una probabilidad del 30 % (AP)), y la gravedad de los daños: posibilidad de fractura (F) y serios daños cerebrales irreversibles (DI)). Cada punto corresponde a una información de configuración, es decir, una situación concreta de juicio: 10 % de probabilidad de tener una fractura, el 30 % de probabilidad de tener un lado de la fractura, el 10 % de tener daño grave e irreversible, un 30 % de probabilidad de tener un grave daño irreversible. Las curvas no son paralelas, estas divergen hacia la derecha. La lógica de la regla multiplicativa es una simple lógica de la multiplicación. Para este ejemplo, se tomarán 1 y 5 como los valores de aversión asociados a los dos estados descritos, las probabilidades de fractura y daño irreversible. Sean 0.1 y 0.3 los posibles pesos obtenidos durante el proceso de integración de la información que conduce al proceso de juicio. Un simple cálculo proporciona los siguientes cuatro valores resultantes:
Las diferencias entre los cuatro
valores tomados en pares no son constantes:
La falta de paralelismo de las curvas en la Figura 12 representa esta falta de constancia. En su forma de abanico abierto hacia la
derecha se observan los efectos de la conjunción.
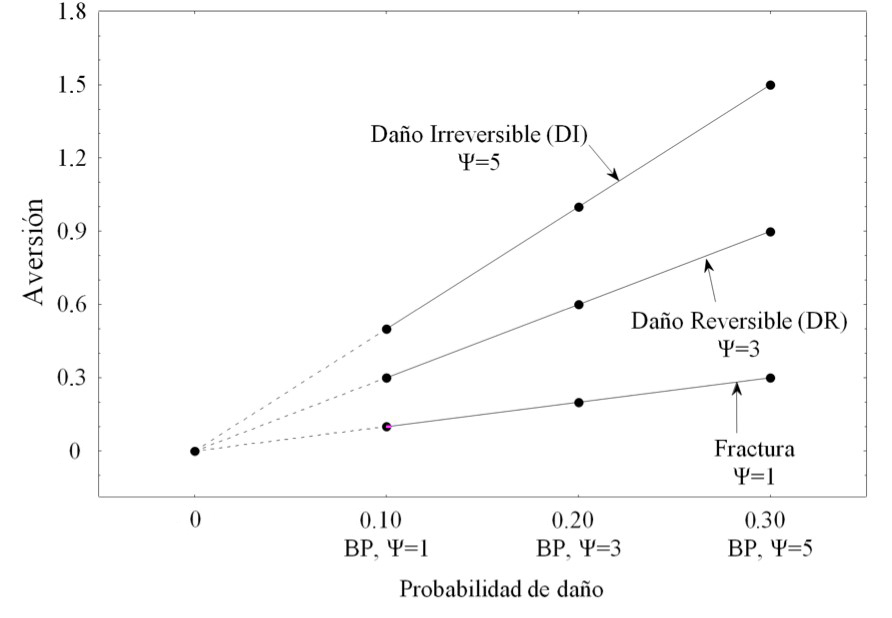 Figura 12
Ilustración de la regla
multiplicativa
Figura 12
Ilustración de la regla
multiplicativa
Fuente: elaboración propia.
La pregunta es entonces: ¿Cómo distinguir la regla multiplicativa de las
conjuntivas? En situaciones simples de dos elementos por cada factor, no es
fácil distinguir el tipo de proceso multiplicativo de otros procesos. Esta
diferencia se hace más fácil y evidente cuando se introducen más de dos
factores en el diseño experimental. Complejizaremos el ejemplo dado
anteriormente, introduciendo un tercer elemento de probabilidad 0.2, y una
tercera modalidad de gravedad de daño, a saber, daño ligero y reversible.
Supongamos que el valor que toma este nuevo elemento es 3 (intermedio entre 1 y
5). El mismo cálculo simple proporciona los siguientes nueve valores
resultantes:
En la Figura 12 (panel inferior), se puede observar la organización de estos
nuevos valores. La forma de la gráfica formada por las curvas continuas tiene
evidentemente, una forma de abanico. Si el trazo de las líneas se extendiera
hacia la izquierda (como se muestra en las líneas punteadas), estas se
cortarían en el mismo punto, y este punto corresponde al valor-opuesto de la
probabilidad cero. Esta propiedad de las líneas es característica de la regla
multiplicativa. En el caso de otras reglas conjuntivas, las curvas no
necesariamente se cruzan en el mismo punto. Otros ejemplos empíricos en los que
se observa la regla multiplicativa sobre los juicios de las decisiones médicas
difíciles se muestran en Sorum, Munoz
Sastre, Mullet y Gamelin (2001) y Frileux, Muñoz Sastre, Mullet
y Sorum (2004).
El cambio de la regla
A continuación, se abordará el por qué, dependiendo de
la situación específica, se podría observar una regla de juicio en lugar de
otra. Se considerarán sucesivamente siete razones posibles e interrelacionadas:
la necesaria adaptación inmediata al contexto (un juicio a corto plazo), el
desarrollo intelectual y emocional (un juicio de largo plazo), la educación (un
juicio de mediano plazo), el aprendizaje intensivo (un juicio específico), la
cultura (un juicio global), las patologías (un juicio ampliamente involuntario)
y sus terapias.
Contexto
Los cambios de reglas en función del contexto contienen, la mayoría de las veces (y a un nivel determinado de desarrollo), las presiones de la propia vida cotidiana. Supongamos que se debe anticipar el desempeño de una persona en un examen difícil, cuya definición será ‘una evaluación en la que pocas personas logran obtener el promedio óptimo o una calificación aprobatoria’. El éxito en dicha evaluación supone una combinación de factores favorables. Si uno de los elementos que son necesarios para el éxito en este examen falla, entonces este triunfo se verá comprometido. Aprobar un examen es considerado convencionalmente como un resultado dependiente de dos grandes tipos de factores: de competencia y motivadores. Por lo tanto, se puede decir que la aprobación de un examen difícil supondrá exhibir unas fuertes habilidades intelectuales y una preparación minuciosa. En la unión de estas afirmaciones se observa la mejor característica de regla conjuntiva, el uso de la conjunción “y”. Por lo tanto, es altamente probable que, en el contexto de la preparación previa para un examen difícil, cuando se conoce la competencia y el grado de preparación, la regla conjuntiva sea la que actúe en la mayoría de los participantes.
La regla conjuntiva es utilizada en diversas situaciones en las que se juzga el desempeño, sin embargo, en la vida cotidiana, hay diversidad de exámenes: difíciles, fáciles o moderados. Entonces, ¿qué regla de juicio se podría encontrar en el caso de una evaluación considerada fácil? La definición misma de un examen fácil es: ‘aquel en el que mucha gente puede obtener una calificación promedio o aprobatoria’. Así pues, el éxito de esa evaluación no implica la necesaria conjunción de elementos favorables, puesto que uno puede tener éxito, porque de todos modos es intelectualmente competente; también, porque de todos modos se ha hecho una buena preparación. Si uno de los elementos que son necesarios está presente, entonces el éxito se convierte en posible. Por lo tanto, se puede decir que el éxito en un examen fácil, dependerá de fuertes habilidades intelectuales o una preparación seria. La unión de estas dos afirmaciones es la principal característica de la regla disyuntiva: la conjunción “o”. Es muy probable que en el contexto del resultado de un examen fácil, de una persona cuya competencia y grado de preparación para el examen se conocen, una regla disyuntiva sea la que mejor describa los resultados.
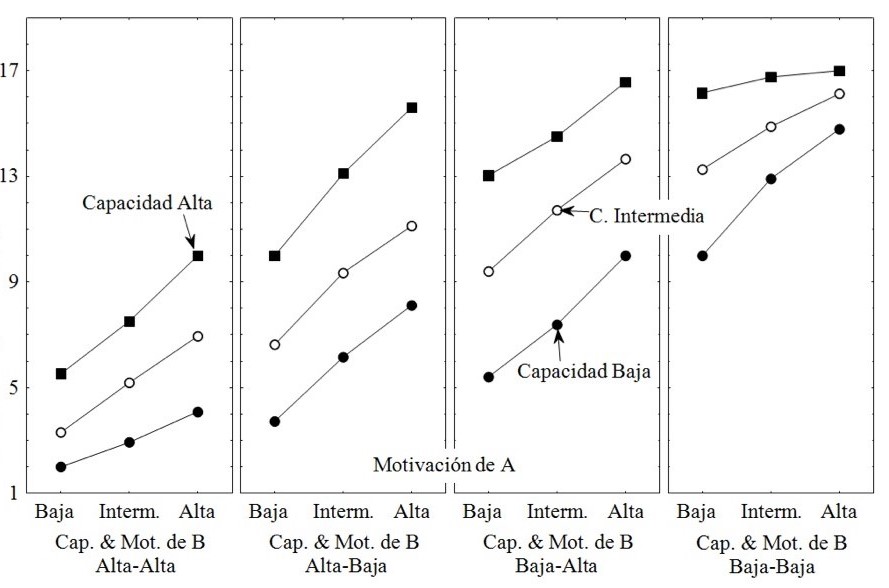
El estudio de Dru et al. (2004) muestra cómo,
en el contexto de rendimiento deportivo, también se pueden dar cambios en las
reglas. En este caso, los atletas profesionales fueron invitados a emitir un
juicio sobre el nivel de rendimiento que se puede esperar de un jugador A (en
comparación con otro jugador B), en función de la capacidad y de la motivación
del jugador. Como se puede ver en la Figura 13, cuando se conoce que el jugador
B está altamente motivado y tiene una alta capacidad, la regla de integración
de la información es la conjuntiva. Cuando se sabe que el jugador B esta poco
motivado y tiene poca capacidad, la regla de combinación de la información es
la disyuntiva. En el caso intermedio, es la regla aditiva la que se observa.
También se pueden observar los resultados obtenidos por Gauché
y Mullet (2005, 2008) para otros ejemplos de los
cambios de regla integración de la información, en función del contexto.
Desarrollo
Las razones por las que una regla de juicio se utiliza en lugar de otra, en una situación constante, también dependen del nivel de desarrollo de la persona que emite el juicio. Supongamos que se debe calcular, solo observando, la superficie de un área rectangular (un espejo, una puerta, una mesa) situada a pocos pasos del observador. De manera casi automática, se hace un barrido con los ojos y sin mucha dificultad es posible hacer un juicio. En la mayoría de las veces la respuesta podría ser: “Es muy pequeño”, o “es suficientemente grande para poder pasar” o “es demasiado grande para el lugar donde se ubica”, así que su juicio dependerá directamente de la superficie percibida.
Aunque esta estrategia de juicio puede parecer para los ojos de un adulto, de bajo esfuerzo y completamente natural, esto no necesariamente es igual para los niños pequeños, aunque sean las mismas condiciones de juicios. Un niño de cinco años, por ejemplo, difícilmente puede hacer este juicio, debido a su desarrollo cognitivo está apenas en proceso, y con respecto al análisis de superficies centraría primordialmente su atención en dos elementos: la altura y anchura. Así, él puede hacer una estimación de estos dos parámetros y luego combinarlos, seguramente en una regla aditiva: “es alto, y es ancho, por lo que es más grande”. Un niño más pequeño tal vez no sea capaz de esta estrategia. Él considerará la dimensión más aparente e impresionante para él; la altura, si da la impresión de que la figura es muy alta o el ancho si visualmente considera que es muy amplio, así dictará su sentencia sin necesidad de tratar de coordinar las dos dimensiones. La regla que se utiliza en dichos casos podría enmarcarse en una regla de tipo disyuntiva.
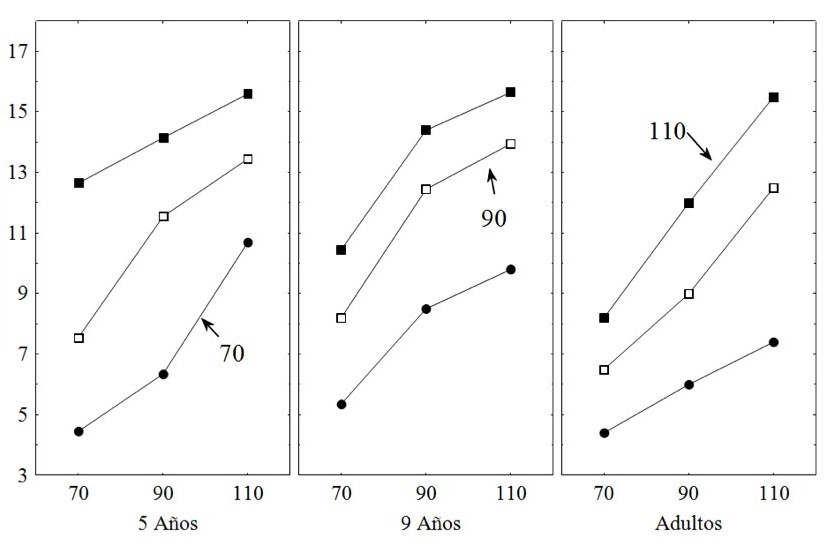
El estudio Rulence-Pâques y Mullet (1998) tuvo como objetivo describir la evolución de
las reglas de juicio de las superficies, usadas por los niños pequeños, los
niños y los adultos. Como se ve en la Figura 14, el patrón de resultados de los
adultos fue el esperable, y se observa la integración de la información
mediante una regla multiplicativa (normativamente correcta). En el caso de los
niños pequeños, la regla mediante la cual se operaron los elementos fue de tipo
disyuntiva. Un rectángulo puede considerarse grande basándose principalmente en
la dimensión más relevante y entonces el juicio depende directamente del
tamaño. En el caso de los niños de nueve años, los resultados muestran un
patrón aditivo y con tendencia hacia la conjuntividad.
También pueden observarse los resultados de Girard y Mullet. (1997), Ligneau-Hervé y Mullet (2005), Ligneau-Hervé, et
al. (2004), Rulence-Pâques, Fruchard,
Dru y Mullet (2005a, 2005b), Przygodski y Mullet
(1997), Girard y Mullet, (2012), con otros ejemplos de las reglas de juicio de evolución-involución.
Aprendizaje
En los dos apartados anteriores, los cambios en las
reglas observadas pueden ser considerados como buenos ejemplos de la capacidad
humana para adaptarse a su entorno diverso y cambiante, y sobrevivir. El
contexto inmediato determinará fuertemente los juicios que se puedan emitir (Dru et al., 2004). Durante un largo período de tiempo, los
humanos se han apoyado en su entorno para adquirir los aprendizajes que
garanticen la supervivencia, principalmente, en los comienzos de la vida, en
los cuidadores. Este soporte permite la supervivencia a largo plazo y una
adecuada preparación a la adaptación, la cual, entonces, puede darse muy
progresivamente, teniendo como substrato biológico la maduración del sistema
nervioso. Esto es lo que se observa en el estudio de Rulence-Pâques
y Mullet (1998). Además de los cambios en relación
con la maduración, los juicios también se modifican en función de la interacción
de los humanos con otros contextos, tales como el educativo. Sabemos que los
procesos de escolarización preparan a los humanos para comprender y procesar
realidades más abstractas e intangibles de las que de la vida cotidiana
familiar podría ofrecer.
Cultura
Dentro de una misma sociedad, las
circunstancias de la vida de cada individuo son diversas, y por supuesto las
sociedades –entre ellas mismas– son muy diferentes. Con el tiempo, algunas
sociedades han transformado su lógica de pensamiento a una principalmente
racional. Este modelo ha sido afirmado por los modelos científicos. En otras
sociedades, la lógica dominante de pensamiento es una forma de pensar que no es
necesariamente racional o que parte de una racionalidad distante de la
científica. Adaptarse a las sociedades, es aprender a pensar y sentir de manera
diferente a las personas que piensan y sienten con la lógica de las sociedades
“racional-científica”. Ouédraogo y Mullet (2001) mostraron cómo estas diferencias en las
lógicas culturales también se integran de acuerdo a las reglas de juicio que
hemos descrito (véanse también Bouazzaoui & Mullet, 2002, 2005). Así que es posible traducir en
términos de reglas generales, las diferencias de pensamientos y sentimientos
característicos de las culturas (Kpanake, Sorum, & Mullet, 2016).
Patología
Aun con los cuidados familiares desde antes del nacimiento y durante el crecimiento, con los procesos de educación, escolarización y los diversos ambientes de intercambio social que puedan tener los humanos, los procesos de interacción con el ambiente también pueden llegar a ser disfuncionales, afectar la calidad de vida y generar altos niveles de sufrimiento individual y colectivo. Una de las formas más comunes en las que se exhibe la disfuncionalidad mencionada es en el abuso de sustancias nocivas para la salud: tabaco, alcohol, drogas, etc. Teniendo en cuenta esto, la pregunta es por las reglas de juicio que se aplican para juzgar comportamientos que afectan directamente la calidad de vida. Podría pensarse, entonces, que las personas dependientes del alcohol tienden a ver cualquier ocasión como una oportunidad para beber, o lo hacen en ocasiones que consideran más o menos estresantes.
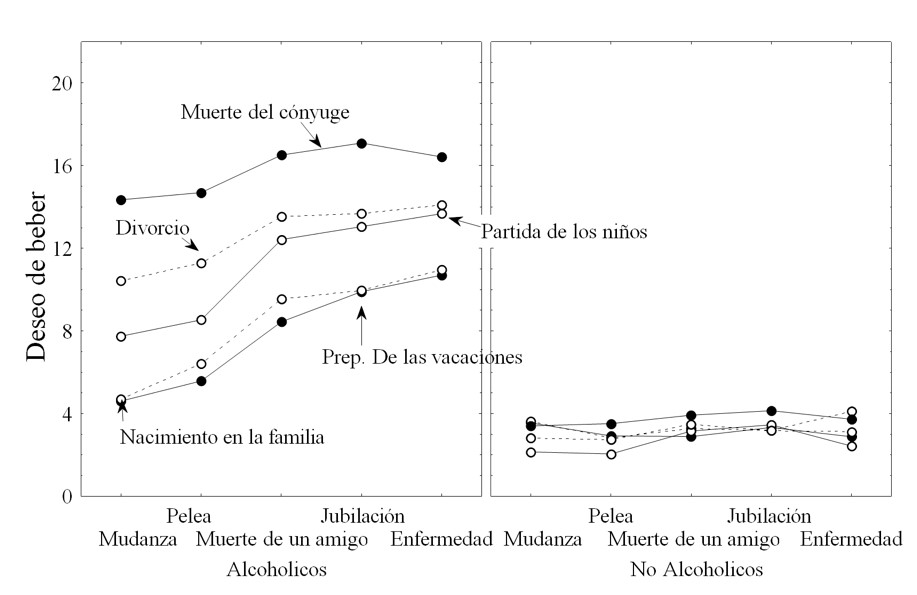
El estudio de Fouquereau, Fernández, Mullet y Sorum (2003) ilustra cómo desde las reglas cognitivas se pueden explicar los juicios frente al problema del alcoholismo. Mujeres alcohólicas tenían que juzgar el grado de incentivo para beber, en función de diversidad de eventos estresantes tales como una mudanza, una pelea con los suegros, la muerte de un amigo, la jubilación, una enfermedad grave, etc. Como se muestra en la Figura 15, la regla de integración utilizada es una regla disyuntiva, similar a la que se observó en el juicio de riesgo de consumo de sustancias. Esta regla es específica para los alcohólicos. En una población de mujeres de la misma edad y el mismo nivel de educación, la regla es radicalmente diferente. Ningún deseo de beber está asociado con acontecimientos estresantes.
Terapia
La última de las razones por las que una regla puede usarse más que la otra –o por la que se cambia la regla de juicio– que se considera a continuación, es el efecto de las terapias, pues tienen como objetivo la modificación del comportamiento de los consultantes. Desde el punto de vista del presente artículo, las reglas de juicio empleadas normalmente por una persona podrían cambiar justamente como resultado del proceso terapéutico.
En el estudio Fouquereau et al. (2003), los participantes alcohólicos recibieron tratamiento para controlar el impulso de beber. La Figura 13 muestra los resultados obtenidos en hombres alcohólicos y la evolución de sus juicios en términos de deseo de beber y en función de las mismas combinaciones de eventos estresantes. Durante el tratamiento, los patrones de juicio son similares a los observados en los participantes sobrios. Estos, sin embargo, no son equivalentes. Todo parece indicar que la información continúa siendo integrada en la misma forma al inicio y al final del tratamiento y que es específicamente la operación de evaluación la que se afecta. La relación cognitiva entre el estrés percibido y el deseo de beber persiste, de un modo que podríamos calificar como silencioso.
Una aproximación individual
Antes de cerrar este artículo teórico, vale la pena hacer énfasis en la perspectiva individual a la cognición cotidiana usando las reglas del juicio. Como se puede constatar –a partir de los numerosos estudios y trabajos realizados hasta este punto– la aproximación de las reglas del juicio es susceptible de contribuir a la unificación de los conocimientos en diversas áreas de la psicología. El nivel de análisis de los fenómenos a los que se aproximan a las reglas de juicio es relativamente molar, pero bastante claro como para poder puntualizar en las comunidades de interés en diferentes campos y bastante riguroso como para permitir una acumulación de conocimientos. La variedad de estudios alrededor del mundo utilizando este marco de análisis, ha permitido ir estableciendo la validez ecológica de las reglas usadas para emitir juicios (Fruchart, Rulence-Pâques, & Mullet, 2007).
Los psicólogos enfocados en el desarrollo pueden encontrar un claro interés en el estudio de la evolución de las reglas cognitivas utilizadas por bebés, niños, adolescentes, adultos y ancianos al juzgar la superficie de diversas áreas, las nociones de conjuntos de objetos y las relaciones causales entre los fenómenos. El psicólogo de la salud puede encontrar un interés evidente en el estudio de las reglas de juicio utilizadas por las personas que padecen alguna enfermedad (y quienes no), para juzgar el grado de bienestar, el grado de dolor que un paciente puede experimentar, el grado de estrés que pueden sentir quienes son dependientes del consumo de una sustancia, en función del contexto o los eventos de la vida cotidiana (véanse Olivari, Muñoz, Guedj, Sorum, & Mullet, 2011). En el área de la psicopatología, también se puede encontrar un interés evidente en el estudio de las reglas utilizadas por las personas que padecen ciertos tipos de enfermedad mental y en una multiplicidad de situaciones de la vida cotidiana. Por ejemplo, las similitudes de los juicios de las personas diagnosticadas con esquizofrenia en comparación con los de quienes no la padecen, o los efectos de las terapias en la capacidad de juzgar de personas diagnosticadas con depresión. En otras áreas como la psicología social, la psicología política, la psicología de los deportes y la psicología del trabajo también se presentan múltiples situaciones que demandan la expresión de un juicio y que puede ser abordado desde esta perspectiva.
Agradecimientos
Este artículo fue escrito en colaboración con el Profesor Wilson
López-López, Editor encargado de la revista Universitas Psychologica. El manuscrito contó con la
revisión doble de pares ciegos. No hay conflictos de intereses.
Referencias
Ahmed, R., Azar, F., & Mullet, E. (2007). Interpersonal forgiveness among Kuwaiti adolescents and adults. Conflict Management and Peace Science, 24(1), 1-12.
Anderson, N. H. (1981). Foundations of information integration theory. Nueva York: Academic Press.
Anderson, N. H. (1982). Methods in information integration theory. Nueva York : Academic Press.
Anderson, N. H. (1991). Contributions to information integration theory. Mahwah: Erlbaum.
Anderson, N. H. (1996). A functional theory of cognition. Mahwah, NJ: Erlbaum.
Anderson, N. H. (2008). Unified social cognition. Mahwah, NJ: Erlbaum.
Azar, F., & Mullet, E. (2001). Interpersonal forgiveness among Lebanese: A six-confession study. International Journal of Group Tensions, 30(2), 161-181.
Azar, F., Mullet, E., & Vinsonneau, G. (1999). The propensity to forgive: Findings from Lebanon. Journal of Peace Research, 36(2), 169-181.
Bouazzaoui, B., & Mullet, E. (2002). Workload, family responsibilities, and anticipated life satisfaction: Contrasting young adults’ and elderly people’s viewpoints. Journal of Happiness Studies, 3(2), 129-152.
Bouazzaoui, B., & Mullet, E. (2005). Employment and family as determinants of anticipated life satisfaction: Contrasting European and Maghrebi people’s viewpoints. Journal of Happiness Studies, 6(2), 161-185.
Dru, V., Pâques, P., & Mullet, E. (2004). The performance schemata in dyadic athletic competition. American Journal of Psychology, 117, 479-496
Falconi, A., & Mullet, E. (2003). Cognitive algebra of love through the adult life. International Journal of Aging and Human Development, 57(3), 277-292.
Fouquereau, E., Fernandez, A., Mullet, E., & Sorum, P. C. (2003). Stress and the urge to drink. Addictive Behaviors, 28(4), 669-685.
Frileux, S., Muñoz Sastre, M. T., Mullet, E., & Sorum, P. C. (2004). The impact of the preventive medical message on intention to change behavior. Patient Education and Counseling, 52(1), 79-88.
Fruchart, E., Rulence-Pâques, P., & Mullet, E. (2007). Ecological validity test of laboratory studies on information integration. Teorie & Modelli [Special Issue on Functional Measurement], 12, 281-288.
Gauché, M., & Mullet, E. (2005). Do we forgive physical aggression in the same way that we forgive psychological aggression? Aggressive Behavior, 31(6), 559-570.
Gauché, M., & Mullet, E. (2008). Effect of context and personality on the forgiveness schema. American Journal of Psychology, 121(4), 607-616.
Girard, M., & Mullet, E. (1997). Forgiveness and its determinants in adolescents, adults, and elderly persons. Journal of Adult Development, 4, 209-220.
Girard, M., & Mullet, E. (2012). Development of the forgiveness schema in adolescence. Universitas Psychologica, 11(4), 1235-1244.
Girard, M., Mullet, E., & Calahan, S. (2002). Mathematics of forgiveness. American Journal of Psychology, 115(3), 351-375.
Guillet, L., Hermand, D., & Mullet, E. (2002). Cognitive processes involved in the appraisal of stress. Stress and Health, 18(2), 91-102.
Hermand, D., Mullet, E., & Coutelle, B. (1995). Perception of the combined effect of smoking and alcohol consumption on health. Journal of Social Psychology, 135, 167-174.
Hermand, D., Mullet, E., & Lavieville, S. (1997). Estimation of the combined effect of tobacco and alcohol on cancer risks. Journal of Health Psychology, 2, 481-491.
Hermand, D., Mullet, E., Sorum, P. C., & Tillard. (2000). Estimation of the combined effect of tobacco and alcohol on cancer risks among alcoholics. European Journal of Applied Psychology, 50, 321-326.
Janet, P. (1889). L’automatisme psychologique. París: Alcan.
Kpanake, L., Sorum, P. C., & Mullet, E. (2016). Breaking bad news to togolese patients. Health Comunication, 31(11), doi: 1311-1317. 10.1080/10410236.2015.1050622
Karpowicz Lazreg, C., & Mullet, E. (2001). Judging the pleasantness of form-color combinations. American Journal of Psychology, 114(4), 511-533.
Ligneau-Hervé, C., & Mullet, E. (2005). Perpective-taking in adults and elderly people. Journal of Experimental Psychology: Applied, 11(1), 53-60.
Ligneau-Hervé, C., Mullet, E., & Sorum, P. C. (2004). Age and medication acceptance. Experimental Aging Research, 30(3), 253-273.
López, W., Pineda Marín, C., Murcia, M. C., Perilla, D. C., & Mullet, E. (2012). Colombian lay people's willingness to forgive different actors of the armed conflict: Results from a pilot study. Psicologica: International Journal of Methodology and Experimental Psychology, 3, 655-663. Recuperado de http://files.eric.ed.gov/fulltext/EJ980499.pdf
López, W., Pineda Marín, C., Murcia, M. C., Perilla, D. C., & Mullet, E. (2013). Forgiving perpetrators of violence: Colombian people's position. Social Indicators Research, 114, 287-301. doi: 10.1007/s11205-012-0146-1
Macri, D., & Mullet, E. (2003). Employment and family as determinants of anticipated life satisfaction among young Greek adults. Community, Work and Family, 6, 197-215.
Makris, I., & Mullet, E. (2003). Judging the pleasantness of contour-rhythm-pitch-timbre combinations. American Journal of Psychology, 116(4), 581-616.
Marquié, L., Sorum, P. C., & Mullet, E. (2007). Emergency physicians’ pain judgment: Cluster analyses of scenarios of acute abdominal pain. Quality of Life Research, 16, 1267-1273.
Mullet, E., & Ciudat, N., & Rivière Shafighi, S. (2004). Cognitive processes involved in the assessment of hazards’ severity. Health, Risk, and Society, 6, 277-288.
Mullet, E., & Neto, F. (1991). Intention to migrate, job opportunities, and aspiration for better pay: An information integration approach. International Journal of Psychology, 26(1), 95-113. doi: 10.1080/00207599108246852
Mullet, E., Rivière, S., & Muñoz Sastre, M. T. (2007). Cognitive processes involved in blame and blame-like judgments and in forgiveness and forgiveness-like judgments. American Journal of Psychology, 120(1), 25-46.
Muñoz Sastre, M. T. & Mullet, E. (1998). Evolution of the intuitive mastery of the relationship between base, exponent, and number magnitude in high school students. Mathematical Cognition, 4, 67-77.
Muñoz Sastre, M. T. (1999). Lay conceptions of well-being and rules used to judge well-being in young adults, middle-aged and elderly people. Social Indicators Research, 47, 203-231.
Neto, F., & Mullet, E. (1998). Decision making as regards migration: Wage differential, job opportunities and the network effect. Acta Psychologica, 98, 57-66. doi: 10.1016/s0001-6918(97)00035-8
Olivari, C., Muñoz, M. T., Guedj, M., Sorum, P. C., & Mullet, E. (2011). Breaking patient confidentiality: Comparing Chilean and French viewpoints regarding the conditions of its acceptability. Universitas Psychologica, 10(1), 13-26.
Przygodski, N., &
Mullet, E. (1997). Aging and moral judgment. European
Journal of
Applied Psychology, 47, 15-22.
Rulence-Pâques, P., Fruchard, E., Dru, V., & Mullet, E. (2005a). Algebraic rules in sport decision-making. Cognitive Algebra in Sport Decision-Making, Theory and Decision, 58(4), 387-406.
Rulence-Pâques, P., Fruchard, E., Dru, V., & Mullet, E (2005b). Decision-making in soccer game: A developmental perspective. European Review of Applied Psychology, 55(2), 131-136.
Rulence-Pâques, P., & Mullet, E. (1998). Perception of surface and inference of surface: The case of the rectangle. Journal of Experimental Child Psychology, 69, 1-27.
Simeone, A., Hermand, D., & Mullet, E. (2001). Judging the probability to be infected through sexual contact. Risk: Health, Safety and Environment, 12, 255-280.
Sorum, P. C., Munoz Sastre, M. T., Mullet, E., & Gamelin, A. (2001). Eliciting patient disutilities for the adverse outcomes of cardiopulmonary resuscitation. Resuscitation, 48, 265-273.
Vinsonneau, G., & Mullet, E. (2001). Willingness to forgive among young adolescents: An European-Maghrebi comparison. International Journal of Group Tensions, 30, 267-278.
Notas
*
Artículo de revisión.
Notas de autor
a
Autor de Correspondencia. Correo electrónico: lopezw@javeriana.edu.co
b
Autora de Correspondencia. Correo electrónico: pinedam.claudiap@konradlorenz.edu.co
Información adicional
Para citar
este artículo: Muñoz Sastre, M. T., López López, W., &
Pineda-Marín, C. (2017). Conceptos básicos de la Teoría Funcional de la
Cognición y algunas de sus aplicaciones. Universitas Psychologica, 16(1),
1-22. http://dx.doi.org/10.11144/Javeriana.upsy16-1.cbtf