Many beliefs or attitudes form and change gradually, with relevant information appearing bit by bit. This may hold even more for children who cannot cope with as much information simultaneously, yet is rarely investigated. This study considers how young children form judgments from successive informers.
There are large literatures on how adults form beliefs from sequential information, both work on attitude formation/change (e.g., Ajzen, 2005; Albarracín, Johnson, & Zanna, 2014; Petty & Briñol, 2010) and on order effects (Anderson, 1981; Hogarth & Einhorn, 1992; Hovland, 1957). These literatures differ in emphasis, because attitude studies see order effects as non-normative nuisance and eliminate them experimentally – the effect of some information should depend on content, not whether it is processed first or second. Nevertheless, order effects are pragmatically important: They are ubiquitous, often large, and appear in, for instance, persuasive communication (Petty, Tormala, Hawkins, & Wegener, 2001), responsibility attribution (Gerstenberg & Lagnado, 2012); category induction (Duffy & Crawford, 2008), affective evaluation (Zauberman, Diehl, & Ariely, 2006); legal decision-making (Pennington & Hastie, 1992), auditing (Trotman & Wright, 2000), or political candidate evaluation (McGraw, Lodge, & Stroh, 1990).
Order effects are non-normative with independent information, but, like other biases, they might have heuristic value (Gigerenzer & Brighton, 2009). Real world serial information is often redundant, making it efficient to settle on an opinion quickly. This yields primacy effects, stronger contributions of initial information. Nevertheless, the world could change. Recency effects, stronger contributions of current information, can then overcome the initial opinion. Primacy/recency together may filter information in a system geared to processing over time (Schlottmann & Anderson, 2007; Wang, Zhang, & Johnson, 2000, 2006). While the adaptive function of primacy/recency has hardly been explored, the view suggests that order effects are integral to serial processing and that both of them should be studied together. This is done here.
Few studies consider either topic with children. The basic ability to update a representation from serial information is fragile, but children adjust their representation of a previously seen object, when told about a changed property, by the end of the second year (Ganea, Shutts, Spelke, & DeLoache, 2007; Ganea & Harris, 2013). It is reasonable to think that by early school age children cope with more complex updating tasks.
Here we consider children’s ability to infer an underlying, unseen property (e.g., niceness of a person) and update this representation repeatedly, from evidence items presented one at a time. When such integration of non-perceptual knowledge with current perceptual evidence is required, one naturally assumes that the here-and-now is more salient to children, similar to the well-documented recency in children’s recall (e.g., Jarrold et al., 2015). Children are not caught in the perpetual present, of course, as they clearly learn, but it is unusual and noteworthy if prior knowledge is strong enough to determine judgment (e.g., Gelman & Markman, 1986; Keil, 1989; Schlottmann, 1999; Chan & Tardif, 2013; Lucas, Bridgers, Griffiths, & Gopnik, 2014).
If prior knowledge is weak, in contrast, recency can make interpretation difficult. Accordingly, many studies neutralize order effects through randomization/counterbalancing, or avoid them with simultaneous information displays. In causal/scientific reasoning or judgment-decision-making, for instance, prior hypotheses are evaluated in light of new observations and in real life this is a multi-step process, unfolding over time, but child studies often summarize data in tables or visual patterns (e.g., Schäuble, 1990; Kuhn, 2010). Children’s personality/social judgments benefit from multiple inputs (e.g., Boseovski & Lee, 2006; Boseovski, Chiu, & Marcovitch, 2013; Cain, Heyman, & Walker, 1997), but that these often appear in succession remains un-studied. Similarly, many studies show that when selecting trustworthy informants, children are finely attuned to subtle cues to credibility (Harris, 2012), but only one considers how trust changes over multiple episodes (Ronfard & Lane, 2018). How children process serial information affects judgment in many areas, but little is known about this. This study focuses on both the serial process and how information order impacts it, studying how children form impressions of people and of a physical property, from brief information sequences.
Serial information does not imply that beliefs are updated whenever new information appears: We could encode each individual item into memory and form an overall opinion only when a relevant question is asked, based on what is recalled. Hastie and Park’s classic paper (1986) distinguished such offline, memory-based judgment from online, spontaneously updated judgment, arguing that the later predominates in everyday life. Purely memory-based judgment appears mainly when the question is unfamiliar and unanticipated, a view endorsed by many (e.g., Albarracín et al., 2014; Mackie & Asunción, 1990; Bizer, Tormala, Rucker, & Petty, 2006; Uleman, Adil Saribay, & González, 2008). It is hard, for instance, to avoid forming an overall impression of a new acquaintance, even from minimal evidence, and this is updated automatically when new information appears, without need for a question. When sampling from a bag of sweets, in contrast, we may accumulate data, but form an opinion on the frequency of lemon sherbets only when a lemon lover asks. Memory-based and serial processing also co-occur: Our view of climate change probably did not form continuously from initial data years ago. More likely, we encoded evidence without reference to this until the concept became topical; only then was relevant knowledge integrated. Subsequent evidence/questions, however, may trigger updating of this overall view. Hogarth and Einhorn’s (1992) influential review of social cognition and decision-making also concluded that updating is more frequent, as people often use it implicitly even when only an end-of-series response is demanded. Such continuous updating is efficient, reducing processing and memory demands, with individual memories not retained (Anderson, 1981, 1996; Busemeyer, 1991).
The present study is the first to look at both serial modes with children, contrasting how they update beliefs online with how they form beliefs when asked for a judgment only once, at the end of the sequence. While serial information is ubiquitous in their life, the precise conditions of judgment from such information vary widely, and we need to learn how these affect children. From the adult literature, one expects recency when beliefs are updated serially, while this is rare with final responding (Anderson, 1981; Hogarth & Einhorn, 1992).
This prediction from work with adults may contrast with the developmentalists’ first intuition, because a simple explanation for recency is that children forget earlier information. For adults, however, the relation of judgment and recall is complex. They correlate if online serial processing is prevented (Hastie & Park, 1986; Mackie & Asunción, 1990; Tormala & Petty, 2001) but are often independent without such constraint (Albarracín et al., 2014; Anderson, 1996; Bizer et al., 2006). If children’s judgment is directly determined by memory, we should see similar order effects whether judgments are serially updated or only a single end-of-sequence judgment is made. If the two serial modes differ from childhood, in contrast, order effects may differ.
A
model of belief revision that represents order effects
To separate information content from order effects, we use a classic additive judgment model (Anderson, 1981, 1996). This has been incorporated into more complex modeling approaches (e.g., Busemeyer, 1991; Hogarth & Einhorn, 1992; Kashima & Kerekes, 1994; Van Overwalle & Labiouse, 2004; Denrell, 2005), but the basic model and its behavioural test suffice here. The model describes the integration of prior belief with evidence, similar to Bayesian approaches. The serial additive model is mathematically simpler, however, and preferred for now because normative Bayesian models do not include order effects.
Under the serial integration model, different bits of information (henceforth informers) combine to a judgment as a weighted sum:
The informers at each position have an information value, ψn, and importance weight, wn (w0ψ0 is for the opinion prior to the first informer). These weights can represent order effects, e.g., recency involves higher weights for recent informers. This model fits adult serial data in many domains (Anderson, 1981, 1996). Here, we apply it with children.
Model tests are not the ultimate goal, however. Rather, if the model fits, one can use it to decompose the judgments and measure primacy/recency weights. In updating designs, these can even be traced temporally. This approach provided seminal evidence that recency in adults’ judgment is often short-term, with stable, long-term attitudes developing as well (Anderson & Farkas, 1973; Dreben, Fiske, & Hastie, 1979). Counterbalancing, to eliminate order effects, is valid because it neutralizes components that often demonstrably have little lasting influence. With children, this remains to be seen.
Equation 1 is general enough to accommodate both continuous belief updating and belief formation at the end of a series. The memory-based approach involves one complex integration of all informers, directly mapping onto Equation 1. Belief updating involves successive two-term integrations, with the model rewritten into a more specific, recursive form; the belief after n informers then reflects an integration of the belief prior to the nth informer and this informer (Anderson, 1996):
A desirable feature of this
belief adjustment version of the model is that it predicts consistency effects,
common in attitude research (e.g., Gawronski & Strack, 2012; McGuire, 1985): Consistent informers have
decreasing effects, but if a second informer is inconsistent, its effect is
large, e.g., if one knows a nice person, learning another nice detail changes
the overall view less than learning of something unkind. Such consistency
effects arise naturally, without any special parameter, because the weights sum
to 1, making this an averaging model. Equation 3 rearranges Equation 2 to show
this. The weight, wn, still only depends
on serial position, but the response adjustment from position n-1 to n varies with the
distance/consistency between current informer, ψn, and previous opinion:
Children’s behaviour fits the
model, showing effects of all informers, plus recency
and consistency effects -- if given help to consider the prior opinion (Schlottmann & Anderson, 1995). Here we study how
children behave under more naturalistic conditions of judgment.
Serial
updating in children
The present study considers two judgment domains, both extensively studied with adults, person impression formation, and non-social judgment of a physical proportion. Person and quantity judgments are as important for children as adults and here are studied together because, despite differences in content, they can have similar structure. Nevertheless, Schlottmann and Anderson (1995; S&A henceforth) found much more recency in social than physical judgment. We follow up on this, adapting S&A’s method.
S&A implemented person judgment in a Christmas setting: Participants helped Santa judge the niceness of story children from sequential evidence. Santa had a series of file cards for each child, one per month, which participants inspected one after the other to learn whether a story child had been “nice”(+) or “naughty”(-), represented visually on the card by different colours. Participants updated their judgment of how nice the story child had been all year on a sliding scale after each sample.
S&A’s binary evidence items involved simple, repetitive stimuli, when in real life information sequences may consist of varied verbal descriptions or observations of different behaviours. However, the serial model holds, with adults, for materials ranging from informationally simple to complex, for sequences of balls of two colours, over series of different adjectives or sentences, to series of paragraphs in connected narrative (reviewed in Anderson, 1996). Child studies first aim to establish competence, so materials with minimal interpretative difficulty are appropriate. Moreover, the nice/naughty, +/- simplification is natural for children, who often use/ask for dichotomous labels of people and behaviours (e.g., Giles & Heyman, 2005). The present study thus keeps to the simple evidence format, focusing for now on whether the model may hold under a wider range of conditions.
To allow model analysis, S&A (and the present study as well) used a factorial design involving multiple sequences of such dichotomous +/- samples: With 4 item series, there are 16 possible permutations (++++, +++-, ++-+, ++--, etc., to ----), corresponding to a position-1 x position-2 x position-3 x position-4 design, with +/- as the levels of each factor (Anderson, 1981). This design maps the additive model of Equation 1 directly onto the additive ANOVA model. If children consider all 4 samples, the model predicts main effects of all samples on judgment at position 4, but no interactions between them. Equivalent additivity tests apply to judgment at earlier positions in updating tasks. In S&A, the model held for 5- to 9-year-olds. In addition, strong recency and consistency effects appeared for younger children.
The S&A study was promising but left important issues open. In particular, it did not elicit naturalistic serial judgments, having the prior belief, and a recursive dependence of responses, built into the procedure, with children adjusting a sliding marker after each sample. Accordingly, we know that 5-year-olds update prior beliefs from current evidence in a mature way, if the prior belief is perceptually available alongside new data. But in everyday life, the prior belief typically comes from memory. A main purpose here is to consider how children update beliefs under a more realistic procedure, requiring purely mental representation of prior beliefs. This may lead to less systematic judgments and/or more reliance on currently visible evidence than in S&A. It is an open question whether children’s judgments will obey the serial model under such more demanding conditions.
A second open issue is the course of development. S&A found decreased recency from 5 to 9 years, but this was difficult to interpret: Younger children used the belief updating, running average strategy of Equation 3 that is established for adults. Older children, however, used an idiosyncratic strategy never seen before, possibly a task-specific adaptation to the slider. We assess here whether older children still show unusual judgments when this is eliminated and the standard adult procedure -- without a marker of the prior belief – is used.
A third question is whether order effects differ between judgment domains. The Christmas scenario just described provides a meaningful, familiar social setting in which visual records of behaviour are kept and inspected, allowing a match to non-social judgment of the same physical cues. In S&A, this non-social task involved a judgment of colour proportion. Recency effects were smaller in this task, but the evidence was also clearly less complex than in the Christmas task, in which the colour represented behaviour. This difference in complexity, rather than any domain difference, might produce stronger recency in the social task. The present study replicates the Christmas task, but introduces a new non-social task better matched in complexity, to assess domain differences in order effects.
Finally, as discussed above, we assess whether children already use two serial modes, continuous belief updating and end-of-series belief formation. Children’s serial and final responses have never been compared. If recency in their judgment reflects memory, then it should appear for updating and end-of-series judgments. Alternatively, if order effects differ, this would fit with a view that the two serial modes seen with adults emerge from childhood.
Method
Participants
Eighty mostly Caucasian children
participated. The younger children (21 girls, 11 boys, mean age 6; 2 years,
range 5; 3 to 7; 11 years) were randomly assigned to one of two tasks. Of the
older children (25 girls, 23 boys, mean age 9; 1 years,
range 8; 0 to 11; 1 years), the first 32 were also randomly assigned to the two
tasks. The remaining 16 participated later in the treasure task, with updating
and end-of-sequences conditions run in reverse order, to test for practice
effects. Children were an opportunity sample, volunteers at a community-based,
central London after-school play-centre, with middle to lower middle-class
intake.
Materials
Two formally identical tasks involved the same physical +/- stimuli, but different narratives. The stimuli were gold star/black dot stickers, each on a white card (10 x 5.5 cm). Each sample sequence involved a new set of 12 cards/stickers, in 3 rows of 4, star/dot side down. Four cards were sampled, one at a time, apparently at random.
In S&A’s Christmas task, each card set represented Santa’s file record for a story child’s behaviour during the months of the year. The card side facing the participant showed the name of the story child. Participants sampled +/- cards for four months to judge how good this story child had been all year. The physical quantity task was a card version of a treasure hunt. The cards represented 12 streets in a city, and star/dot represented golden treasure or old black rock. The card side facing participants showed different house/tree configurations. Participants searched four streets to judge how much treasure was hidden in the city overall.
The response scale was a 35cm dowel with 1cm segments. A 5cm gold disc marked the all good/treasure end; a black disc marked the all naughty/rock end. Participants pointed to a dowel location to show how good a story child had been last year/how much treasure was hidden in a city. Ratings were read from the back to the nearest cm. Children can use such scales from 4 years (Anderson & Schlottmann, 1991). This scale differed from S&A, where the dowel had a slider showing the old response until it was updated. Here, in contrast, children pointed, typically removing their finger as each sample was removed
Design
Each sequence has 4 +/- samples. The 4
serial positions of these samples correspond to 4 factors, with +/- factor
levels, in a factorial design, yielding 16 different sequences
in total (see Table 1).
Table 1
The
16 sample sequences shown to children, corresponding to a position-1 x
position-2 x position-3 x position-4 factorial design, with +/- levels for each
factor; children in sample group 1 saw only sequences with consistent or even
composition; children in sample group 2 saw sequences with one inconsistent
sample
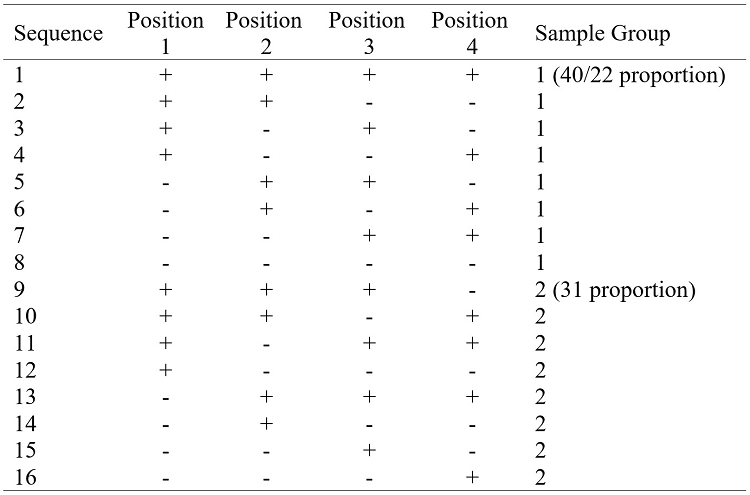
Each child saw 8 of the sequences; sample-group 1 judged 2+2- and 4+ or 4- proportions, and sample-group 2 judged 3+1- or 3-1+ proportions. Each group thus judged a complete position-1 x position-2 x position-3 factorial. Both groups combine to the full 4-factor design, such that the main effect of position-4 corresponds to the 4-way interaction of the group with the other positions. This confounding was preferred over tiring children in a long session.
Participants judged each sequence in two ways: Initially, they updated their judgment after each sample. Thus, when the first update in the sequence is the DV, sample at position-1 is the only within subjects factor, analyses of the second update as DV includes sample at position-1 and position-2, and so on. Sample-group (1, 2), age (older, younger) and task (social, physical) are additional between subjects factors in mixed model factorial analyses.
After completing updating for all 8 sequences, children saw them all again, this time making only a single, end-of-series judgment for each. These end-of-series judgments could be influenced by the preceding updating task. To evaluate this, an additional group of older children made end-of-series judgments first, serial judgments second, for the treasure task.
Procedure
Children were tested in individual, 20 to 30 minute sessions. First, a puppet (“Lucy”) invited children to play a treasure hunt game, or needed help figuring out, for Santa, how nice some children had been all year long (testing was in winter). One story child’s record was shown, with 12 cards for 12 months. Two cards were turned over to reveal gold/black, meaning that the story child had been mostly nice/naughty that month. In the treasure game, similarly, children learned that the card set represented a city, seeing samples of treasure/rock hidden in its streets. A new card set, for a different story child or city, was then chosen, the cards laid out, and Lucy modeled sampling (apparently at random) and judgment for an anchor sequence (6 gold samples), starting from the scale midpoint “because we don’t know anything about this child/city yet”. Upon finding the first gold, Lucy explained “Gold/good! I think there is more gold in this city/this child has been mostly good, because this street already has gold/the child was good in this first month already. But we have only one clue, so we don’t know very much about the whole city/the rest of the year yet.” Then Lucy explained the scale “this is how we show how much gold we think there is/how good we think a child has been. We point to this bar. This end means every street has gold/the child has been good all year long. This end means every street has only old black rock/the child has been naughty all year long. I think this city has more gold, but I don’t know about most of the streets yet,” while pointing at below ¾ of the scale. Lucy removed the old sample, revealed a new sample, pointed, etc, with decreasing adjustments and comments (e.g., we found gold/the child was good – now we know a bit more, but we still don’t know whether the whole city has gold/the child has always been good, because we have not looked at many streets/months). The child aided by the puppet then judged a second anchor sequence (6 black), then practiced judgments without model for a 3+/3- sequence. Corrections were made if adjustment was directionally incorrect, or the child pointed to the extremes on the first sample, but rarely needed. The puppet went to sleep and the child continued, without feedback, with the experimental sequences.
Afterwards, children heard “you did well, so we can make it harder. I tell you about some more cities/children, but this time you only make one guess at the very end, after we have looked at several streets/months.” Children saw all sequences again, making only one judgment for each sequence.
Results
Four updates per sequence allow a rich set
of analyses: We begin by describing the raw data patterns for the 16 sequences.
We then test the model for judgment at each position, subsequently using it to
decompose the judgment and measure the weights for each evidence sample. Next,
we look at the adjustments in judgment from one position to the next, to assess
whether children, like adults, use the running average strategy. Finally, we compare
children’s updating responses with their end-of-series responses for the same
sequences.
Complete
judgment patterns
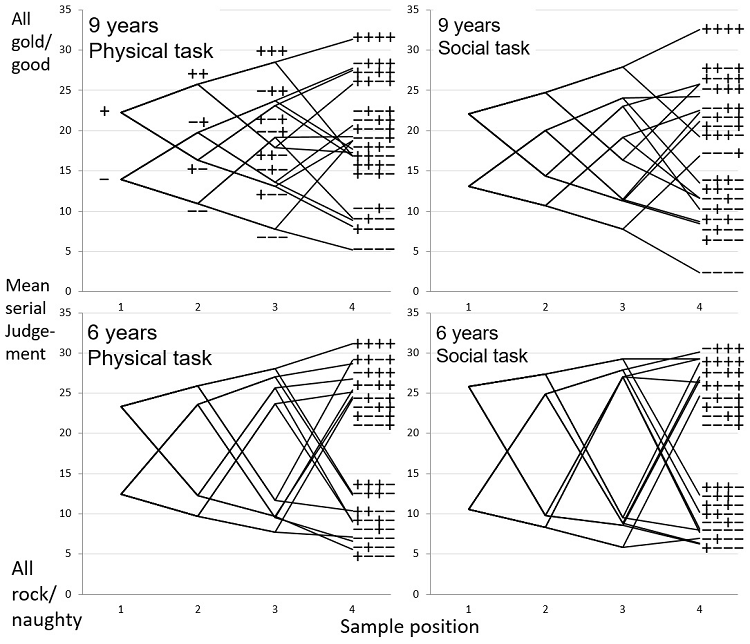 Figure 1
Children’s
mean judgments of “How much gold is hidden in this city?”/”How nice was this
child all year?” Each diagram shows how judgments were updated after samples 1
to 4 (horizontal) in 16 unique sequences (listed on the right of each panel)
Figure 1
Children’s
mean judgments of “How much gold is hidden in this city?”/”How nice was this
child all year?” Each diagram shows how judgments were updated after samples 1
to 4 (horizontal) in 16 unique sequences (listed on the right of each panel)
Figure 1 shows children’s mean judgments after each sample (horizontal) for all different sequences seen at this position. Thus, at position-1, there are two means, for the first + or – sample. At position-2, there are four means for four sequences, as the initial +/- sample is followed by another + or -, splitting into 8 and 16 unique sequences at position-3 and -4, respectively (listed on the right). Each line that can be traced on the graph shows how children updated their judgments from the first to the fourth sample in a sequence. The top line, for instance, shows judgments increasing steadily for the 4+ sequence, while the line branching downwards at position-2 is for the ++-- sequence.
Figure 1 shows four main results: First, judgments reflect, as they should, size and composition of the preceding sequence. At the point of judgment, children saw only the current sample, but with minor exceptions, they responded to new positive information by increasing, to negative information by decreasing the unseen prior judgment. For instance, the top and bottom lines for 4+ and 4- sequences show more extreme judgments as sample size grows. Sequence composition effects appear in that judgments are typically highest for 4+ sequences, decreasing for 3+1-, 2+2-, 1+3-, and 4- sequences. This is clearer for the older children (top panels, see labels on the right).
The second main finding is recency. Sequences with the same composition do not elicit the same judgments, but judgments depend on sample ordering, with stronger effects of later samples. To illustrate, position-2 judgments (second from left on horizontal) for -+ sequences were higher than for +- sequences, with the smallest F(1, 15) = 6.23, MSE = 14.61, ηpartial
2
= 0.29 (all p < 0.05 unless noted, throughout the paper.) This position-2 recency, in comparison of -+ and +- sequences, is larger for younger children, with an age x sequence interaction for both ages/tasks, F(1, 60) = 22.21, MSE = 27.37, ηpartial
2
= 0.27.
The recency seems slightly larger in the social task (left panel), but this was not significant, F(1, 60) = 2.63, MSE = 27.37, ηpartial
2
= 0.04, p = 0.11. Throughout this study, task differences were in the same direction, but smaller than in S&A and non-significant. The absence of task differences is our third finding.
Position-3 and -4 judgments also show recency, i.e., judgments are typically higher when positive, lower when negative information comes later. As at position-2, the recency is stronger for younger children: Strikingly, their judgments form two distinct clusters, for sequences with + or - final informer. Thus, non-normative order effects are larger than normative sample composition effects, which nevertheless appear within the clusters. Younger children are also less affected by sample size, with fairly extreme judgments appearing from the first sample, especially in the social task. These age differences, discussed further below, are our fourth finding.
The raw judgment patterns in Figure 1 are complex because they include children’s reaction to sequence content and order. If the additive model of Equation 1 holds, however, we can simplify and separate these effects. The first step was to test the additive model, which predicted no interactions between serial positions: Indeed, while both ages showed main effects of all samples on judgments at all positions, only 2 of the 64 interactions between them were significant (see Appendix). Thus the model held, replicating S&A.
Serial
position weights
The model was then used to decompose the judgments and derive the weight of each serial position (Figure 2, see Appendix for details of how weights were computed). The R4 curve gives the weights for 4 samples on judgment at position-4. The R3 curve gives the weights for 3 samples on judgment at position-3, and so on. In each curve, the highest weight is for the current sample. This is the recency from Figure 1, shown more clearly. These recency weights are slightly higher in the social task, and much higher for younger children.
The novel feature of Figure 2 is that it traces the temporal development of the recency, highlighting that this is largely short-term. Compare, for instance, the position-3 weight in the R3 and R4 curves. In the R3 curve, the position-3 sample is the current informer, and the weight is high, reflecting strong recency. In the R4 curve, however, when the next sample appears, the position-3 weight does not remain elevated, but comes right down. The upswing of the terminal position weight is temporary in all curves. Once it disappears, the weight curves are flat, with informers having similar weights on judgment, for both tasks/ages.
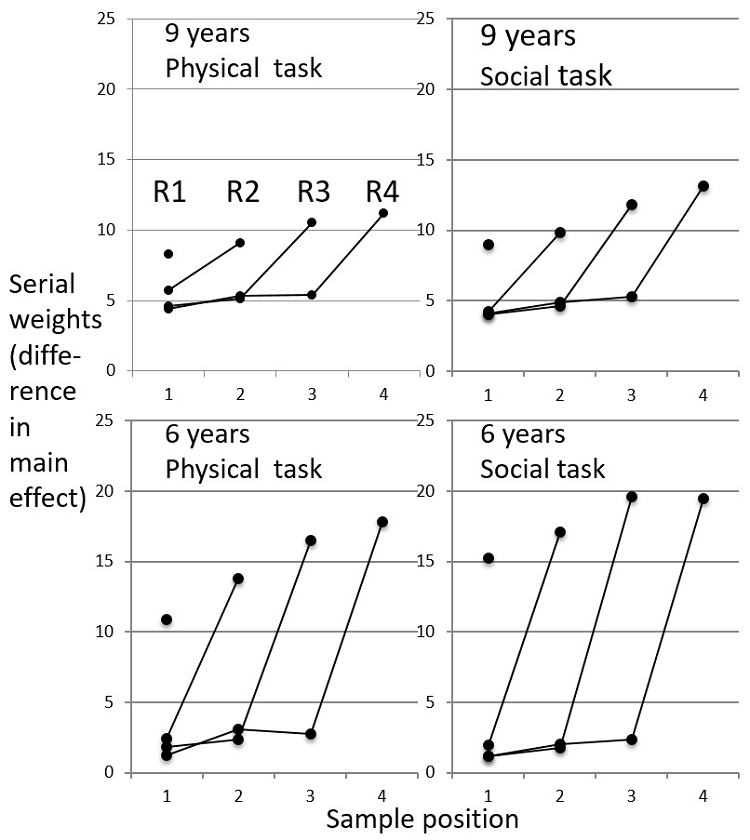 Figure 2
Serial weight curves. The R4 curve shows
weights for 4 informers (horizontal) on the response at position 4, the other curves do the same for earlier responses. These
weights are the difference between the effect of + and – informers at a given
position (see Appendix for further explanation). The upswing of the curves at
the final position, with flat curves at earlier positions, indicates short-term
recency.
Figure 2
Serial weight curves. The R4 curve shows
weights for 4 informers (horizontal) on the response at position 4, the other curves do the same for earlier responses. These
weights are the difference between the effect of + and – informers at a given
position (see Appendix for further explanation). The upswing of the curves at
the final position, with flat curves at earlier positions, indicates short-term
recency.
These flat curves are a key point: If the terminal recency at R3 (or R2 or R1) was incorporated into the attitude visible at the next response R4 (or R3 or R2), then these curves would continue to slope over the non-terminal positions, with ever-decreasing weights for earlier informers. That the curves are flat, in contrast, implies that the recency dissipates before the next belief adjustment. Thus there are two components to the attitude, a short-term component with strong recency, and a stable long-term component without it.
Both ages show this two-component structure, with one clear age difference: The flat weights of non-terminal informers in Figure 2 are twice as large for older children. While a stable attitude develops for all, this is weaker for younger children.
These observations were confirmed by statistical comparison of the 4 terminal recency weights (rightmost points of each curve) and, separately, of the 6 other, non-terminal weights (the permanent attitude component), with age/task as additional IVs. There were no task differences, but main effects of age appeared in both analyses, F(1, 60) ≥ 20.8, MSE = 108.24, ηpartial
2
= 0.26, with stronger recency and a weaker permanent attitude at the younger age.
The terminal recency weights increased from R1 to R4 (upward trend in top points), F(3, 180) = 42.9, MSE = 6.42, ηpartial
2
= 0.42, more so for younger children, F(3, 180) = 2.77, MSE = 6.42, ηpartial
2
= 0.04. Notably, the much smaller differences between non-terminal weights (flat parts of the curves) were significant as well, F(5, 300) = 3.02, MSE = 5.22, ηpartial
2
= 0.05, with initial position-1 weights for R3 and R4 sequences 0.5 lower than the others. A small amount of recency was therefore incorporated into the permanent attitude and did not dissipate. This did not differ between tasks/ages.
In sum, the serial weight analysis showed that the extreme recency in children’s updating responses was largely short-term, obscuring, not precluding a permanent attitude. These analyses were possible because children’s data fit the general additive model of Equation 1.
Continuous
belief updating
The next question is whether children, like adults, use the more specific running average model of Equation 3 to update beliefs. Continuous updating was not built into the procedure, but two aspects of the data argue that children used this.
First, there were serendipitous behavioural indications of belief adjustment. Thirteen younger children (41%, mean age 6 years 4 months) and 21 older children (66%, mean 9 years 1 month) used a finger as a sliding marker at least once, keeping it on the scale when an informer was removed and adjusting position after the next informer. This typically appeared for some samples in some sequences, not consistently for all/most trials. When children with/without finger-sliding were compared statistically, finger-sliding children had smaller recency for judgment at all positions, with F(1, 62) ≥ 8.64, MSE = 86.23, ηpartial
2
= 0.12.Finger-sliding children thus gave more mature judgments.
Secondly, adjustments from one sample to the next showed consistency effects, with more adjustment to the same sample if it was less consistent with the prior sequence. This is a major prediction of the belief adjustment model of Equation 3, as discussed in the introduction. Accordingly, there should be more adjustment at position 2 to samples inconsistent with the preceding sample (+- or -+) than to consistent samples (-- or ++), with equivalent predictions for longer sequences, e.g., the same position-4 sample should elicit more adjustment if inconsistent with all 3 prior samples than only 2, just one, or none.
Figure 3 plots absolute size of adjustments from a response to the next, in the order predicted by the model. Darker bars, for more discrepant samples, should show more adjustment than lighter bars for less discrepant samples. In the top and middle panels, position-2 and -3 adjustments grow to the right, as predicted, for both ages/tasks. At the bottom, for position-4, ordering is as predicted at age 6, with two inversions at age 9. Recall, however, that two groups of children saw different sequences at position-4, and inverted effects appeared between groups, while the predictions held within groups. The inversions could thus reflect group differences, not model deviations. This requires further work. For now, both the finger-pointing data and consistency effects support the belief updating model.
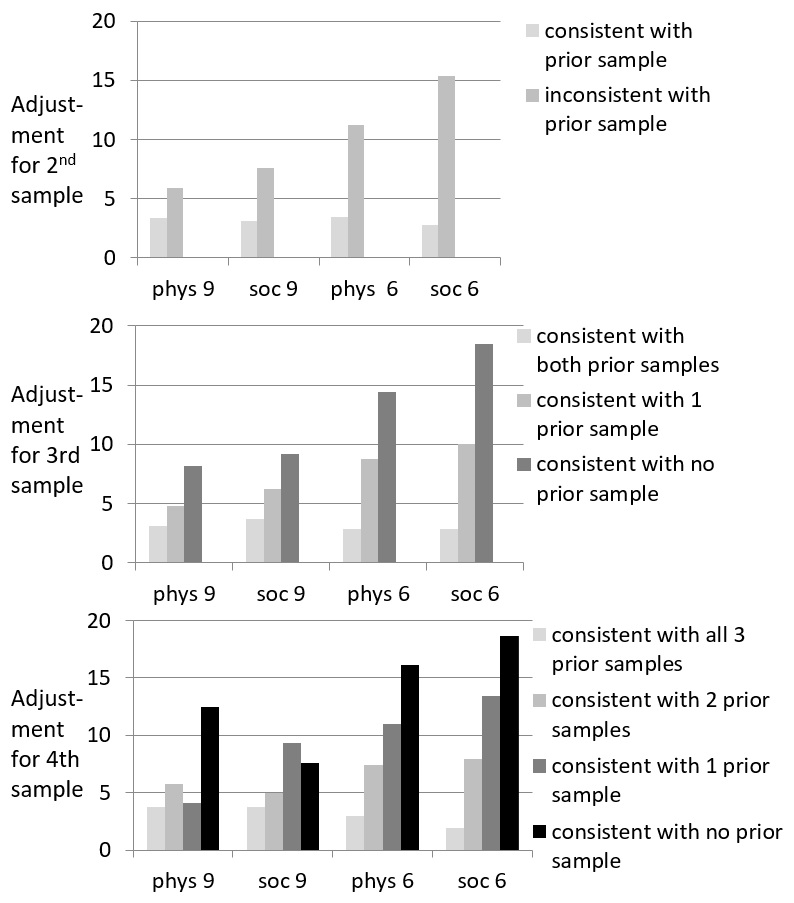 Figure 3
Size of adjustment to samples at position 2 to 4
(top to bottom) for two ages and tasks. The running adjustment model predicts increasing adjustment from left to
right in each block, as inconsistency with prior samples increases (darker bars
are less consistent)
Figure 3
Size of adjustment to samples at position 2 to 4
(top to bottom) for two ages and tasks. The running adjustment model predicts increasing adjustment from left to
right in each block, as inconsistency with prior samples increases (darker bars
are less consistent)
End-of-Series judgments
Our final question was whether children, like adults, already use two modes of serial judgment. Thus, after the updating task, children saw all sequences again, giving one end-of-series judgment per sequence, to see whether order effects take the same form as for updating. The additive model also fit these final responses, with main effects of all 4 informers, F(1, 56) ≥ 143.77, MSE = 41.08, ηpartial
2
= 0.12, but no interactions (only 4 F > 1). Figure 4 compares the weights for final (black curves) and serial responding (halftone, these are the R4 updating weights from Figure 2). The curves clearly differ: Final responding produces less recency and higher non-terminal weights, for both ages/tasks.
The largely flat weight curves for final responding showed hints of a u-shape, i.e., primacy and recency, but the position effect was not significant, F(3, 180) = 2.48, MSE = 18.34, ηpartial
2
= 0.04, p = 0.062. That weights were lower for younger children was also not significant, F(1, 60) = 2.47, MSE = 38.2, ηpartial
2
= 0.04, p = 0.12; there were no other effects either.
Statistical comparison of serial and final weights confirmed the difference between the curves in Figure 4, with a position x response mode interaction, F(3, 180) = 47.56, MSE = 19.68, ηpartial
2
= 0.44, that differed with age, F(3, 180) = 6.02, MSE = 19.68, ηpartial
2
= 0.09, due to the previously discussed age differences in serial responses. This underscores that order effects differ between serial and final judgments. (The contributing response mode and position main effects, plus the age x position interaction also reached significance. The only other effect was a task x position interaction, with a less regular pattern in the treasure task when weights combined over response mode. This is the only significant task difference in any of the analyses in this paper).
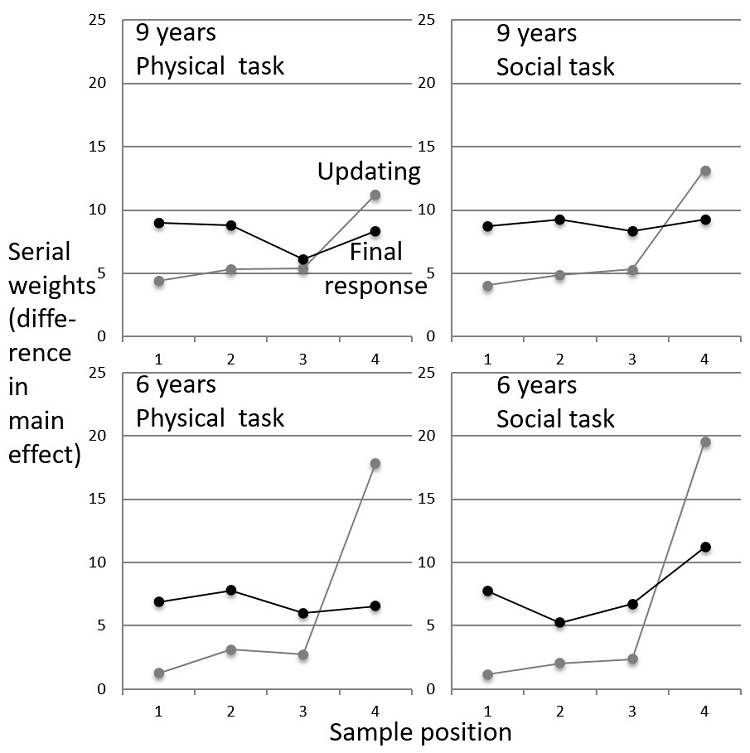 Figure 4
Serial weight curves for responses after all 4 samples,
for serial updating (half-tone, repeated from Figure
2) and for end-of-series responses. Updating came first.
Figure 4
Serial weight curves for responses after all 4 samples,
for serial updating (half-tone, repeated from Figure
2) and for end-of-series responses. Updating came first.
The curve differences in Figure 4 could reflect two serial modes — or practice effects, because after extensive experience, children may have switched to a more normative approach late in the session. Another group of older children thus gave end-of-series responses first. Serial weight curves (Figure 5) were similar to those in Figures 2 and 4, for the same age/task and opposite order of response modes, and did not differ statistically (F(3, 90) < 1.68, MSE = 8.39, ηpartial
2
= 0.05, p = 0.176). The curve differences thus reflect effects of response mode per se.
Model fit for updating responses was good in this new group of children, with only one of 16 interactions between positions, F(1, 14) = 5.49, MSE = 13.12, ηpartial
2
= 0.28. However, the model did not fit their final responses well, with 3 of 6 significant interactions; the smallest had F(1, 14) = 5.24, MSE = 9.78, ηpartial
2
= 0.27. The model may not hold in this case.
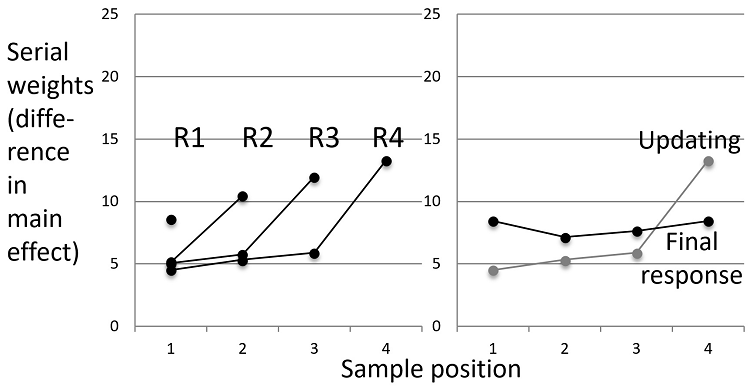 Figure 5
Serial weights for a new group of 9-year-olds in the
physical treasure task, responding after each sample (left) or giving an
end-of-series response (right). End-of-series judgments came first in this group of
children, but this did not affect the weights (compare with Figures 2 and 4).
Figure 5
Serial weights for a new group of 9-year-olds in the
physical treasure task, responding after each sample (left) or giving an
end-of-series response (right). End-of-series judgments came first in this group of
children, but this did not affect the weights (compare with Figures 2 and 4).
Regardless of this, final
responding eliminated the recency in all groups of
children. All in all, the data suggest therefore that children, like adults,
use two different approaches for judgment from serial information.
Discussion
Much real-world information unfolds over
time, but how children cope is rarely studied. The introduction raised four
questions about their serial processing. Results show, first, that children can
make systematic serial judgments even if this involves multiple updates of
purely mentally represented prior beliefs. Second, there is developmental continuity
in the serial process, but change in its serial weight parameters. Thirdly, no
differences appeared between social and non-social judgment domains. Finally,
children, like adults, respond differently when continuously updating beliefs
or giving only one judgment at the end of the series. These findings are
discussed in turn.
Children
can update mentally represented beliefs
Children from early school age systematically updated mental representations, without an external representation of the prior belief to aid them. This adds to prior findings of simpler updating abilities from the toddler age (Ganea et al., 2007). Here, children repeatedly updated representations of a quantitative, non-perceptual property (niceness or amount of treasure), in a way that reflected changes in sample proportion and size over time.
Our results agree with a recent study in which 5-year-olds updated their trust in an informant’s claim from extended observation of behaviour (Ronfard & Lane, 2018). Children guessed, over 4 trials, the location of a sticker under cup A or B, based on what an informant told another agent; this informant was inaccurate on one of 4 trials. In a video, on trial 1, the informant looked under each cup and told the other agent where the sticker was, then the video stopped to allow the child to guess the location. When the video started again, the other agent looked under the cup designated by the informant (which reveals accuracy if integrated with the earlier verbal statement), the informant apologized for the error (in some conditions), and finally the child judged the informant’s niceness, smartness and intention (on some trials). Trial 2 followed immediately and a new sticker was hidden. The informant again looked, said were it was, the child guessed again, etc. The child’s guess on trial 2 thus potentially reflects trustworthiness as inferred from trial 1, and so on, for later trials. Despite multiple steps between accuracy information and judgment, children chose the location designated by the informant more often when the informant was more accurate over preceding trials. This extends S&A and the present finding, that children’s judgment reflects sample proportion, to another domain and to information of greater interpretative complexity.
In Ronfard and Lane’s (2018) work, children saw complex behaviour, but each child judged only one sequence, so the data give limited information on process. The present data are complementary, with children judging multiple, simpler sequences, which allows process analysis. This suggests that children use a running average updating approach, like adults.
In evidence, first, children spontaneously finger-marked the prior opinion. This indicates running adjustment, but not its mathematical form, which was determined from formal model tests. These upheld the additive model of Equation 1. Consistency effects constrained the model qualitatively to its running average form, with larger belief revisions for inconsistent evidence, as for adults. All ages may thus use a similar belief adjustment process.
Finger-marking is not needed for belief adjustment, of course, but children are unlikely to use it without a compatible internal approach, so our index is conservative. Self-generated use of an external marker may reduce processing load and, indeed, finger-marking children showed less recency. It is, of course, unclear whether finger-marking allows better weighting of prior opinion/evidence, or whether some children – more able ones perhaps – discover external marking and show less recency. Other children may use belief adjustment internally or – halfway between internal/external – could visually fixate prior scale location. Either way, overt signs of running adjustment in almost half of the younger children are impressive given low levels of strategy use at this age (Bjorklund, 1990). High levels of serial strategy from early on fit with a view that serial processing is frequent in everyday life.
Development of serial strategies may resemble that of memory strategies (Bjorklund, 1990): These first appear in contexts triggering them automatically, with deliberate control over use achieved later. The same may hold for judgment. Continuous updating may emerge in online reactions to rapidly unfolding perceptual sequences, during narratives or episodes of observation/interaction. While the prior belief is mentally represented, crucially, it remains activated from one informer to the next one and does not need to be recalled each time. The familiar Christmas/treasure contexts, with informers in quick succession, may fit this description.
Adults also use running adjustment in deliberate, controlled ways, even when prior beliefs must repeatedly be retrieved from memory, with distractor tasks (Dreben et al., 1979). Ronfard and Lane’s (2018) finding that children tracked trustworthiness over a sequence with multiple interpolated (albeit related, not distracting) steps suggests that children may already have such ability. This requires further work.
While continuous belief adjustment as a running average is efficient, with recursive integration minimizing memory/processing demands at each step, it may contribute to the recency effects so often found for adults, as for children here. Running adjustment can produce normative responses, but only if current sample and prior belief are weighted proportionally to sample size; the current sample weight must decrease as the sequence grows, because the sample already condensed in the prior belief has increased. Recency appears if this weight reduction is insufficient, e.g., if current evidence is given equal weight throughout. But running adjustment produces only a summary representation at each step; sample size must be tracked separately. Young children may not do this, or not do it well. The ubiquity of recency effects in adult belief updating suggests this remains difficult later.
Developmental
aspects
Despite children using the same updating process as adults, we also found developmental changes: Older children showed less short-term recency and stronger long-term beliefs.
Our finding of major recency at age 6 does not contradict the absence of recency for similar-aged children in Ronfard and Lane (2018). Recency, found here, and elsewhere for adults, is typically short-term and dissipates by the next sample. Ronfard and Lane did not measure children’s trust right after the informant’s (un)trustworthiness became clear, but only after several interpolated events, including the informant’s next statement. Therefore, one would not expect much recency in their data, and the two studies fit well.
The recency in the present study reduced substantially from age 6 to 9. One may wonder, however, about older or younger ages. By standardizing weights (to % of scale range) different ages can be compared across published studies with similar procedure
1
. This shows far stronger recency here than in S&A with younger children. The recency weight for 6-year-olds here was 50% of scale range, reducing to 30% by age 9, similar to 5-year-olds in S&A. The extreme recency here likely reflects increased processing load without external marker.
To estimate development past age 9, two sets of adult studies, with materials of different complexity, are relevant. If tested on the present task, adults would likely focus exclusively on the visual black/gold feature, ignoring the childish Christmas/treasure narratives. They may then simply estimate colour frequency, as in Shanteau (1970, 1972), who found only minor recency. This comparison suggests a large reduction in recency beyond age 9.
Identical tasks do not guarantee identical processing, however, and arguably, children did not treat the stars as un-interpreted visual features, but as cues to hidden treasure/past deeds. In this case, appropriate comparison is to studies of attitude formation from verbal descriptions (Anderson & Farkas, 1973; Dreben et al., 1979). In these, recency weights for adults were 20% to 30%, similar to older children here. From this perspective, 9-year-olds’ processing approximates a mature level for semantically interpreted attitude informers. Both comparisons are relevant, with informational complexity mediating serial processing.
In addition to the recency component, we can compare long-term belief strength across the age range. This is generally more similar in children and adults. Six- and 9-year-olds here had long-term weights of about 7% and 14% of scale range, falling within the adult range (7% to 15%; Anderson & Farkas, 1973; Dreben et al., 1979; Shanteau, 1970, 1972). With slider support, children reached adult levels even earlier, with 11% and 14% for 5 and 6/7-year-olds (Schlottmann & Anderson, 1995). Stable belief weights did increase with age, but these changes were small relative to changes in the recency component.
The introduction considered that order effects, like other biases, may have heuristic value and one may further speculate about the value of age-related change in this. In particular, children are learners, whereas adults have become knowers: The same world, due to lack of experience, is less redundant for children. While it can be efficient for knowledgeable adults to fixate beliefs early, children may typically do better to leave beliefs open to later revision, when they have learnt more about the situation. More recency in children is not just a stronger non-normative bias, but could be adaptive, facilitating children’s role as learners.
Adjustment
for Growing Sample Size
One aspect of our results does not fit this story: As mentioned, if the prior opinion involves more and more evidence, then new informers normatively carry less and less weight. This appeared in all adult studies, but for children, here and in S&A, the recency increased with sequence length.
Children thus may not understand all implications of sample size, despite some sensitivity (Jacobs & Narloch, 2001; Lawson & Fisher, 2011; Lawson, 2014), including our and Ronfard and Lane’s (2018) finding of more extreme judgments for longer series. As previously discussed, children may find tracking sample size difficult, but if they ignored this factor, constant, not increasing recency would ensue. Perhaps children focus on the wrong aspect of uncertainty, taking a growing sample not just to increase statistical certainty, but also to increase task difficulty and subjective uncertainty (Bayless & Schlottmann, 2010). This requires further work.
Different
judgment domains: Social and non-social
This study found no support for a view that biases may be stronger in social judgment which may be harder to quantify (Jacobs & Potenza, 1991). Slightly more recency appeared in the social than physical task, but in contrast to S&A, domain differences were not significant. S&A’s non-social task involved judging uninterpreted colour proportion per se, but in their social task colour illustrated behaviour, which is arguably more complex. Here, colour illustrated behaviour or treasure and children could imagine examples of both. If prior task differences in recency reflect differences in information complexity, then we found little here because complexity matched better across tasks.
Domain differences cannot be ruled out entirely. The social task concerned personality traits, and while pre-schoolers occasionally appreciate their dispositional nature (Cain et al., 1997; Liu, Gelman, & Wellman, 2007), traits may seem more changeable than physical features, with recent information more relevant to labile traits than constant non-social properties. The lack of domain differences here could reflect high processing load, with ceiling level recency suppressing domain differences. Both possibilities remain open.
Two
strategies for serial processing in children
A final, crucial result was the contrast of strong recency in serially updated beliefs with no recency when beliefs were expressed only at the end. This difference replicates findings with adults. However, not only is recency eliminated, but classic work shows primacy effects in adults’ final responses (e.g., Asch, 1946; Anderson, 1981; Hogarth & Einhorn, 1992). Is this a developmental difference?
For adults, primacy reflects attention decrement across positions (Anderson, 1981; Dreben et al., 1979; Riskey, 1979). Manipulations to reduce this eliminate primacy as well, e.g., none appears with final responding, if adults verbalise, not just read, informers. Children here often spontaneously verbalised that the story child had been good/that there was treasure etc., which would eliminate attention decrement. Moreover, the present sequences were short, within children’s memory limits, while adult studies typically have 6 to 9 informer sequences. These procedural elements rather than development could explain the absence of primacy here. The childhood origins of primacy effects in impression formation have never been studied. This needs further work urgently.
Besides eliminating short-term recency, final responding also affected the stable beliefs: It produced higher weights, with weights for 6-year-olds higher than for 9-year-olds’ updating responses (Figure 4). That end-of-series responding produced even evidence weighting and stronger beliefs would seem a practical advantage in work with children. It remains to be seen whether this advantage generalizes to longer, more demanding sequences.
The difference between serial and final responding has implications for children’s strategy. Serial responding clearly involves online updating. With final responding, children could update implicitly, or use a memory-based approach. While many (Anderson, 1981; Bizer et al., 2006; Busemeyer, 1991; Hastie & Park, 1986; Uleman et al., 2008) argue that memory-based strategies are rare in familiar, predictable judgments, the exception is for simple materials that do not tax memory (Hogarth & Einhorn, 1992). Children clearly had no memory problem here, order and age effects differed, and no child used finger-marking with final responding, so we submit that children used a memory-based approach, aggregating informers only at the end. Two modes of serial judgment thus may appear from childhood.
Two objections to this position are conceivable. Under a Piagetian view, the memory-based strategy is beyond young children, who cannot cope with more than one informer at a time. However, even pre-schoolers can integrate multiple simultaneous informers (Ebersbach, 2009; Schlottmann, 2001). Another argument against a memory-based strategy is that one does not generally know whether another informer is imminent. Children here knew, however, from the prior updating trials, how long the series would be, so “holding off” judgment was viable. Moreover, teachers often admonish children to wait with an answer until all facts are in, perhaps focusing school-aged children on memory-based strategies. Processing capacities and executive functions will limit this for children even more than for adults, but our results tentatively suggest that 6-year-olds can form an intention to inhibit judgment and act on this, with benefits for the belief acquired. Further work to delineate the conditions under which children defer belief updating is clearly possible and desirable.
Conclusions
Here, children revised judgments of continuous population properties from serial sample evidence. Such inferences are ubiquitous in social cognition (Dozier, 1991; Boseovski & Lee, 2006; Cain et al., 1997; Master, Markman, & Dweck, 2012), and appear in non-social domains. Even infants draw inferences from sample to population proportion (Xu & García, 2008). But serial information also affects tasks with different structure, e.g., how children evaluate binary hypotheses in scientific/causal reasoning (Kalish, 2012) or generalize information (Lawson, 2014).
The present study found strong recency, but this did not determine judgments, it merely overlaid them temporarily. Children effectively built up beliefs reflecting sample size and proportion, when updating beliefs and when deferring judgment to the end. The practical implication of this and of Ronfard and Lane (2018) is that serial processing needs not to be avoided with children.
The developmental role of recency highlighted here is only one piece of the puzzle of serial processing. Judgment of complex informers, of longer sequences, of situations with strong (rather than neutral) prior beliefs, as well as the developmental emergence of primacy, and the functional role of primacy/recency in different environments should be studied next.
Acknowledgements
Thanks to the children and staff at Coram’s
Fields for their kind participation and help. This paper is dedicated to Norman
H. Anderson. Thanks for the support and the inspiration.
References
Ajzen, I. (2005). Attitudes, personality, and behavior. Berkshire, England: McGraw-Hill Education.
Albarracín, D., Johnson, B. T., & Zanna, M. P. (Eds.). (2014). The handbook of attitudes. New York, NY: Psychology Press.
Anderson, N. H. (1981). Foundations of information integration theory. New York, NY: Academic Press.
Anderson, N. H. (1996). A functional theory of cognition. Mahwah, NJ: Erlbaum.
Anderson, N. H., & Farkas, A. J. (1973). New light on order effects in attitude change. Journal of Personality and Social Psychology, 28(1), 88-93.
Anderson, N. H., & Schlottmann, A. (1991). Developmental study of personal probability. In N. H. Anderson (Ed.), Contributions to information integration theory: Volume III: Developmental (pp. 111-134). Hillsdale, NJ: Erlbaum.
Asch, S. E. (1946). Forming impressions of personality. Journal of Abnormal and Social Psychology, 41(3), 258-290.
Bayless, S., & Schlottmann, A. (2010). Skill-related uncertainty and expected value in 5- and 7-year-olds. Psicologica. Special Issue on Functional Measurement, 31(3), 677-687.
Bizer, G. Y., Tormala, Z. L., Rucker, D. D., & Petty, R. E. (2006). Memory-based versus on-line processing: Implications for attitude strength. Journal of Experimental Social Psychology, 42(5), 646-653.
Bjorklund, D. F. (Ed.). (1990). Children’s strategies. Hillsdale, NJ: Erlbaum.
Boseovski, J. J., & Lee, K. (2006). Children’s use of frequency information for trait categorisation and behavioural prediction. Developmental Psychology, 42(3), 500-513.
Boseovski, J. J., Chiu, K., & Marcovitch, S. (2013). Integration of behavioral frequency and intention information in young children's trait attributions. Social Development, 22(1), 38-57.
Busemeyer, J. R. (1991). Intuitive statistical estimation. In N. H. Anderson (Ed.), Contributions to information integration theory (Vol. I, pp. 187-215). Hillsdale, NJ: Erlbaum.
Cain, K. M., Heyman, G. D., & Walker, M. E. (1997). Preschoolers’ ability to make dispositional predictions within and across domains. Social Development, 6(1), 54-75.
Chan, C. C., & Tardif, T. (2013). Knowing better: The role of prior knowledge and culture in trust in testimony. Developmental Psychology, 49(3), 591-601.
Denrell, J. (2005). Why most people disapprove of me: Experience sampling in impression formation. Psychological Review, 112(4), 951-978.
Dozier, M. (1991). Functional measurement assessment of young children’s ability to predict future behaviour. Child Development, 62(5), 1091-1099.
Dreben, E. K., Fiske, S. T., & Hastie, R. (1979). The independence of evaluative and item information: Impression and recall order effects in behavior-based impression formation. Journal of Personality and Social Psychology, 37(10), 1758-1768.
Duffy, S., & Crawford, L. E. (2008). Primacy or recency effects in forming inductive categories. Memory & Cognition, 36(3), 567-577.
Ebersbach, M. (2009). Achieving a new dimension: Children integrate three stimulus dimensions in volume estimations. Developmental Psychology, 45(3), 877-883.
Ganea, P. A., & Harris, P. L. (2013). Early limits on the verbal updating of an object’s location. Journal of Experimental Child Psychology, 114(1), 89-101.
Ganea, P. A., Shutts, K., Spelke, E. S., & DeLoache, J. S. (2007). Thinking of things unseen: Infants' use of language to update mental representations. Psychological Science, 18(8), 734-739.
Gawronski, B., & Strack, F. (Eds.). (2012). Cognitive consistency: A fundamental principle in social cognition. New York: NY: Guilford Press.
Gelman, S. A., & Markman, E. M. (1986). Categories and induction in young children. Cognition, 23(3), 183-209.
Gerstenberg, T., & Lagnado, D. (2012). When contributions make a difference: Explaining order effects in responsibility attribution. Psychonomic Bulletin & Review, 19(4), 729-736.
Gigerenzer, G., & Brighton, H. (2009). Homo heuristicus: Why biased minds make better inferences. Topics in Cognitive Science, 1(1), 107-143.
Giles, J. W., & Heyman, G. D. (2005). Preschoolers use trait‐relevant information to evaluate the appropriateness of an aggressive response. Aggressive Behavior, 31(5), 498-509.
Harris, P. L. (2012). Trusting what you're told: How children learn from others. Cambridge, MA: Harvard University Press.
Hastie, R., & Park, B. (1986). The relationship between memory and judgment depends on whether the judgment task is memory-based or on-line. Psychological Review, 93(3), 258-268.
Hogarth, H. J., & Einhorn, R. M. (1992). Order effects in belief updating: The belief-adjustment model. Cognitive Psychology, 24(1), 1-55.
Hovland, C. I. (Ed.). (1957). The order of presentation in persuasion. New Haven, CT: Yale University Press.
Jacobs, J. E., & Narloch, R. H. (2001). Children’s use of sample size and variability to make social inferences. Applied Developmental Psychology, 22(3), 311-331.
Jacobs, J. E., & Potenza, M. (1991). The use of judgment heuristics to make social and object decisions: A developmental perspective. Child Development, 62(1), 166-178.
Jarrold, C., Hall, D., Harvey, C. E., Tam, H., Towse, J. N., & Zarandi, A. L. (2015). What can we learn about immediate memory from the development of children's free recall? The Quarterly Journal of Experimental Psychology, 68(9), 1871-1894.
Kalish, C. W. (2012). How young children learn from examples: Descriptive and inferential problems. Cognitive Science, 36(8), 1427-1448.
Kashima, Y., & Kerekes, A. R. Z. (1994). A distributed model of averaging phenomena in person impression formation. Journal of Experimental Social Psychology, 30(5), 407-455.
Keil, F. C. (1989). Concepts, kinds and cognitive development. Cambridge, MA: MIT Press.
Kuhn, D. (2010). What is scientific thinking and how does it develop? In U. Goswami (Ed.), Blackwell Handbook of Childhood Cognitive Development (2nd Edition, pp. 492-523). Hoboken, NJ: Wiley-Blackwell.
Lawson, C. A. (2014). Three-year-olds obey the sample size principle of induction: The influence of evidence presentation and sample size disparity on young children’s generalizations. Journal of Experimental Child Psychology, 123, 147-154.
Lawson, C. A., & Fisher, A. V. (2011). It’s in the sample: the effects of sample size and diversity on the breadth of inductive generalisation. Journal of Experimental Child Psychology, 110(4), 499-519.
Liu, D., Gelman, S. A., & Wellman, H. M. (2007). Components of young children’s trait understanding: Behavior-to-trait inferences and trait-to-behavior predictions. Child Development, 78(5), 1543-1558.
Lucas, C. G., Bridgers, S., Griffiths, T. L., & Gopnik, A. (2014). When children are better (or at least more open-minded) learners than adults: Developmental differences in the forms of causal relationships. Cognition, 131(2), 284-299.
Mackie, D. M., & Asunción, A. G. (1990). On-line and memory-based modification of attitudes: Determinants of message recall-attitude change correspondence. Journal of Personality and Social Psychology, 59(1), 5-16.
Master, A., Markman, E. M., & Dweck, C. (2012). Thinking in categories or along a continuum: Consequences for children’s social judgments. Child Development, 83(4), 1145-1163.
McGraw, K. M., Lodge, M., & Stroh, P. (1990). On-line processing in candidate evaluation: the effects of issue order issue importance and sophistication. Political Behavior, 12(1), 41-58.
McGuire, W. J. (1985). Attitudes and attitude change. In G. L. Lindzey & E. Aronson (Eds.), The handbook of social psychology (3rd ed., Vol. II, pp. 233-346). New York, NY: Random House.
Pennington, N., & Hastie, R. (1992). Explaining the evidence: Tests of the story model for juror decision making. Journal of Personality and Social Psychology, 62(2), 189-206.
Petty, R. E., & Briñol, P. (2010). Attitude change. In R. Baumeister, & E. Finkel (Eds.), Advanced Social Psychology: The State of the Science (pp. 217-259). New York, NY: Oxford University Press.
Petty, R. E., Tormala, Z. L. Hawkins, C., & Wegener, D. T. (2001). Motivation to think and order effects in persuasion: The moderating role of chunking. Personality and Social Psychology Bulletin, 27(3), 332-344.
Riskey, D. R. (1979). Verbal memory processes in impression formation. Journal of Experimental Psychology: Human Learning and Memory, 5(3), 271-281.
Ronfard, S., & Lane, J. D. (2018). Preschoolers continually adjust their epistemic trust based on an informant’s ongoing accuracy. Child Development, 89(2), 414-429. https://doi.org/10.1111/cdev.12720
Schäuble, L. (1990). Belief revision in children: the role of prior knowledge and strategies for generating evidence. Journal of Experimental Child Psychology, 49(1), 31-57.
Schlottmann, A. (1999). Seeing it happen and knowing how it works: How children understand the relation between perceptual causality and knowledge of underlying mechanism. Developmental Psychology, 35(5), 303-317.
Schlottmann, A. (2001). Perception Versus Knowledge of Cause and Effect in Children: When Seeing Is Believing. Current Directions in Psychological Science, 10(4), 111-115.
Schlottmann, A., & Anderson, N. H. (1995). Belief revision in children: Serial judgment in social cognition and decision making domains. Journal of Experimental Psychology: Learning, Memory, and Cognition, 21(5), 1349-1364.
Schlottmann, A., & Anderson, N. H. (2007). Belief learning and revision studied with Information Integration Theory. Teorie & Modelli, Special Issue on Applications of Functional Measurement in Psychology, 12(1-2), 63-76.
Shanteau, J. (1970). An additive model for sequential decision making. Journal of Experimental Psychology, 85(2), 181-191.
Shanteau, J. (1972). Descriptive versus normative models of sequential inference judgment. Journal of Experimental Psychology, 93(1), 63-68.
Tormala, Z. L., & Petty, R. E. (2001). On-line versus memory-based processing: The role of “need to evaluate” in person perception. Personality and Social Psychology Bulletin, 27(12), 1599-1612.
Trotman, K. T., & Wright, A. (2000). Order effects and recency effects: Where do we go from here? Accounting and Finance, 14(2), 169-182.
Uleman, J. S., Adil Saribay, S., & González, C. M. (2008). Spontaneous inferences, implicit impressions, and implicit theories. Annual Review of Psychology, 59, 329-360.
Van Overwalle, F., & Labiouse, C. (2004). A recurrent connectionist model of person impression. Personality and Social Psychology Review, 8(1), 28-61.
Wang, H., Zhang, J., & Johnson, T. R. (2000). Human belief revision and the order effect. Proceedings of the Twenty-second Annual Conference of the Cognitive Science Society. Philadelphia, PA: University of Pennsylvania.
Wang, H., Zhang, J., & Johnson, T. R. (2006). The order effect in human abductive reasoning: An empirical and computational study. Journal of Experimental & Theoretical Artificial Intelligence, 18(2), 215-247.
Xu, F., & García, V. (2008). Intuitive statistics by 8-month-old infants. Proceedings of the National Academy of Sciences of the United States of America, 105(13), 5012-5015.
Zauberman, G., Diehl, K., & Ariely, D. (2006). Hedonic versus informational valuations: Task dependent preferences for sequences of outcomes. Journal of Behavioral Decision Making, 19(3), 191-211.
Statistical Appendix
Model
Tests
Mixed model ANOVAs were done on judgments at each position, with age, task and sample group as between subjects factors. The position-1 judgments had only the first informer as within subjects factor, position-2 judgments had first and second informers, and so on. Because informers at all positions were identical, equal-sized main effects of all informers on judgment at position-n indicate no order effects, while a larger effect of informer n indicates recency. If earlier informers not only have smaller main effects than later informers, but lack main effects entirely, then the recency has wiped out the contributions of early informers.
The additive model of Equation 1 can be tested because the present factorial design (see Table 1) maps directly onto the ANOVA model and any ANOVA interactions of the serial positions factors mark deviations from additivity. Accordingly, if the serial integration model holds, samples at different positions that contribute to judgment at this position should have main effects, while there should be no interactions of these serial informers on judgments at any position.
Results supported the model. ANOVA on position-1 judgments finds only a position-1 main effect, larger in younger children, F(1, 56) > 10.9, MSE = 14.5, ηpartial
2
= 0.16 (all results, throughout, are reported at p < 0.05). Analysis of position-2 judgments finds effects of both samples and interactions with age, reflecting a larger position-2 effect, smaller position-1 effect for younger children, F(1, 56) > 9.65, MSE = 12.6, ηpartial
2
= 0.15, plus a task main effect of little concern, F(1, 56) = 4.13, MSE = 4.57, ηpartial
2
= 0.07, due to 0.5 higher judgments in the treasure task. The complete ANOVA model for the position-1 x position-2 x age x task x sample group design includes 8 effects involving interactions of positions-1 and 2. These could falsify the model, but only one was significant, age x sample group x position-1 x position-2, F(1, 56) = 4.69, MSE = 3.91, ηpartial
2
= 0.08, without clear pattern.
At position-3, again significant main effects of all 3 serial factors appeared, all differing between the ages, F(1, 56) > 13.2, MSE = 19.06, ηpartial
2
= 0.19, with position-1 and -2 effects smaller, position-3 effect larger for younger children. Task differences were absent, except for a task x sample group x position-3 interaction (the position-3 effect was about 4 points smaller in the treasure task for the group that would later see 2:2/4:0 sequences at position-4, F(1, 56) = 6.34, MSE = 56.68, ηpartial
2
= 0.1). More importantly, there were a total of thirty-two interaction effects involving 2- or 3-way interactions of at least two serial positions that could falsify the model, but all of these were non-significant. Only 5 had F > 1.
The same pattern of results also appeared for judgment at position-4: There were main effects of all 4 factors, each qualified by an interaction with age, F(1, 56) > 11.76, MSE = 17.43, ηpartial
2
= 0.17, with the position-4 effect larger, the other effects smaller at the younger age. Only one effect involving an interaction of at least two serial positions appeared, task x age x sample group x position-3 x position-4, F(1, 56) = 6.03, MSE = 8.5, p = 0.017, ηpartial
2
= 0.09, with no clear pattern. Of course, information on high order interactions at this position is missing (as each child only judged half of the design, see method). Overall, only 2 of 64 interaction tests across judgment at all positions were significant. Thus there was good model support in children’s serial updating responses.
Follow-up Tests for Individual Ages
Because the main effects of the 4 serial positions generally differed by age, it is possible that for the younger children informers at earlier serial positions made no significant contribution to judgment at the later positions. However, when the younger children’s data were analysed separately, effects of all serial informers on judgment at all 4 positions still appeared, F(1, 28) > 8.15, MSE = 11.36, ηpartial
2
= 0.23. Across judgment at all positions, only one interaction of the serial positions reached significance, F(1, 28) = 7.08, MSE = 4.59, ηpartial
2
= 0.2. Thus, even the younger children considered all informers, with judgments described by the serial model.
Serial Weight Curves. Because the serial integration model held, it could be used to decompose the judgments and derive the serial weights. The difference in marginal means for + and – samples at position n (in other words, the ANOVA unstandardized main effect of informer n) reflects both sample weight and value in Equation 1. But since identical stimuli were used at all serial positions, the difference between the values of the + and – sample is constant. This makes the serial position weights in Equation 1 proportional to the ANOVA serial position main effects.
For instance, for R4 responses, after the fourth informer, 9-year-olds in the physical task gave mean judgments of 23.72 to sequences with + and of 12.52 to sequences with - as fourth and final informer, which gives a weight of 11.2. For sequences with + and – informers at position-3, in contrast, they gave R4 judgments of 20.81 and 15.42, yielding a much lower weight of 5.61. For sequences with + and – as position-2 and -1 informers, the weights came to 5.33 and 4.39, respectively, declining only slightly from position 3 to 1. These values yield the R4 curve in Figure 2, showing recency, with a much higher weight for the final informer.
The same calculations were also done to derive the weights of informers contributing to the earlier R3, R2 and R1 responses, yielding the family of curves in the top left panel of Figure 2. The same calculations were also done for the final responses in Figures 4 and 5, but, of course, with only one response we can derive only one curve.
Notes
1
I
thank J. Shanteau for this suggestion.
*
Research
article.
Author notes
a
Correspondence author.
Email: a.schlottmann@ucl.ac.uk
Additional information
How
to cite: Schlottmann, A. (2018). How Children Form
and Update Beliefs from an Evidence Series. Universitas Psychologica,
17(4). https://doi.org/10.11144/Javeriana.upsy17-4.cfub





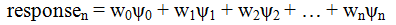 [Equation 1]
[Equation 1]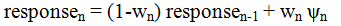 [Equation 2]
[Equation 2]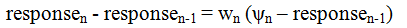 [Equation 3]
[Equation 3]





